Transverse magnetic mode excitation in an atomic mirror

doi:10.15406/paij.2022.06.00269

eISSN: 2576-4543

Physics & Astronomy International Journal

Mini Review Volume 6 Issue 4

Transverse magnetic mode excitation in an atomic mirror

S. Ghezali,

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

M Slimani

¹Physics Department, Faculty of Sciences, University Saâd Dahlab of Blida, Algeria
²Lycée Mohamed Boudiaf, Ksar-El-Boukhari, Algeria

Correspondence: S Ghezali, Physics Department, Faculty of Sciences, University Saâd Dahlab of Blida, Road of Soumaa, Blida 09000, Algeria

Received: November 02, 2022 | Published: November 14, 2022

Citation: Ghezali S, Slimani M. Transverse magnetic mode excitation in an atomic mirror. Phys Astron Int J. 2022;6(4):156-160. DOI: 10.15406/paij.2022.06.00269

Download PDF

Abstract

We present a study of a transverse magnetic mode excitation in a multi-layer atomic mirror. We give the continuity relationships at the interfaces of the setting.¹ We deduce the transverse and parallel components of the electric field through the atomic mirror and then the total component. We show that there is no enhancement of the electric field in the vaccum contrarily to the transverse electric field excitation.²

Introduction

We introduce a detailed study of a transverse magnetic mode excitation in an atomic mirror. It is easy to demonstrate that in this geometry, we have: $\frac{\partial}{\partial y} = 0$ $\frac{\partial}{\partial y} = 0$ . There are two independant solutions of the Maxwell equations.¹ One introduces a TE excitation (E_y, B_x and B_z). The other one gives a TM excitation (B_y, E_xand E_z) coupled between them.

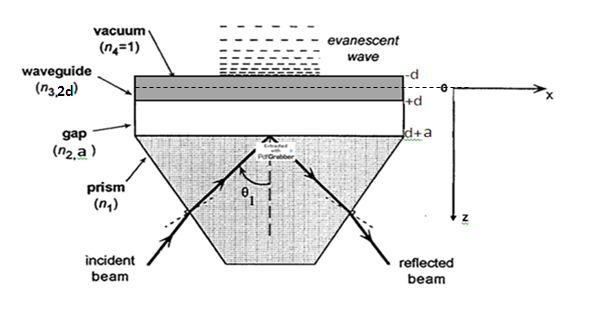
Figure 1 Resonant dielectric structure: the waveguide (Ti0₂, refraction index n₃=2.387 and thickness 2d=67.9nm) is separated from the glass prism (LaSFN18, refraction index n₁=1.893) by a layer of low index, the gap, (SiO₂, thickness a=700nm, refraction index n₂=1.49). The dielectric layers are deposited by a laser beam at $λ$ $λ$ =780nm. The fourth medium is vacuum (refraction index n₄=1).

Maxwell equations:

The Maxwell equations [1, 3] give:

$\to \nabla \land \to E = - \frac{1}{C} \frac{\partial \to B}{\partial t}$ $\vec{\nabla} \land \vec{E} = - \frac{1}{C} \frac{\partial \vec{B}}{\partial t}$

$\to \nabla \land \to H = \frac{4 π}{C} \to J + \frac{1}{C} \frac{\partial \to D}{\partial t}$ $\vec{\nabla} \land \vec{H} = \frac{4 π}{C} \vec{J} + \frac{1}{C} \frac{\partial \vec{D}}{\partial t}$

$\to \nabla . \to E = 4 π ρ$ $\vec{\nabla} . \vec{E} = 4 π ρ$

$\to \nabla . \to B = 0$ $\vec{\nabla} . \vec{B} = 0$

In order to introduce the right relationships, we present the electric field in the multi-layer system for a TE excitation.

$E(1)y=Aexp(−iγ1z)+A\exp(iγ1z)$ $E_{y}^{(1)} = A e x p (- i γ_{1} z) + A^{\} e x p (i γ_{1} z)$

$E(2)y=Bexp(β2z)+B\exp(−β2z)$ $E_{y}^{(2)} = B e x p (β_{2} z) + B^{\} e x p (- β_{2} z)$

$E(3)y=Cexp(−iγ3z)+C\exp(iγ3z)$ $E_{y}^{(3)} = C e x p (- i γ_{3} z) + C^{\} e x p (i γ_{3} z)$

$E_{y}^{(4)} = D e x p (β_{4} z)$ $E_{y}^{(4)} = D e x p (β_{4} z)$

For a transverse magnetic mode excitation, we give the two components of the electric field deduced from the Maxwell equations. The magnetic field B_yfor the TM excitation has the same form as the perpendicular electric field E_yfor the TE excitation.¹ See the above equations.

${\to E}_{T} = E_{x} \to i + E_{z} \to k$ ${\vec{E}}_{T} = E_{x} \vec{i} + E_{z} \vec{k}$

$\to \nabla \land \to E = ∣ ∣ ∣ ∣ ∣ \begin{matrix} \begin{matrix} \begin{matrix} i \frac{\partial}{\partial x} E_{x} \end{matrix} & \begin{matrix} j \frac{\partial}{\partial y} 0 \end{matrix} \end{matrix} & \begin{matrix} k \frac{\partial}{\partial z} E_{z} \end{matrix} ∣ ∣ ∣ ∣ ∣ \end{matrix} = i (\frac{\partial E_{z}}{\partial y}) - j (\frac{\partial E_{z}}{\partial x} - \frac{\partial E_{x}}{\partial z}) + k (- \frac{\partial E_{x}}{\partial y}) = i K_{0} \to B$ $\vec{\nabla} \land \vec{E} = | \begin{matrix} \begin{matrix} \begin{array}{l} i \\ \frac{\partial}{\partial x} \\ E_{x} \end{array} & \begin{array}{l} j \\ \frac{\partial}{\partial y} \\ 0 \end{array} \end{matrix} & \begin{array}{l} k \\ \frac{\partial}{\partial z} \\ E_{z} \end{array} | \end{matrix} = i (\frac{\partial E_{z}}{\partial y}) - j (\frac{\partial E_{z}}{\partial x} - \frac{\partial E_{x}}{\partial z}) + k (- \frac{\partial E_{x}}{\partial y}) = i K_{0} \vec{B}$

$E(1)x(z)=γ1K0n21(−Aexp(−iγ1z)+A\exp(iγ1z))$ $E_{x}^{(1)} (z) = \frac{γ_{1}}{K_{0} n_{1}^{2}} (- A e x p (- i γ_{1} z) + A^{\} e x p (i γ_{1} z))$

$E(2)x(z)=β2iK0n22(Bexp(β2z)−B\exp(−β2z))$ $E_{x}^{(2)} (z) = \frac{β_{2}}{i K_{0} n_{2}^{2}} (B e x p (β_{2} z) - B^{\} e x p (- β_{2} z))$

$E(3)x(z)=γ3K0n23(−Cexp(−iγ3z)+C\exp(iγ3z))$ $E_{x}^{(3)} (z) = \frac{γ_{3}}{K_{0} n_{3}^{2}} (- C e x p (- i γ_{3} z) + C^{\} e x p (i γ_{3} z))$

$E_{x}^{(4)} (z) = \frac{β_{4}}{i K_{0} n_{4}^{2}} D e x p (β_{4} z)$ $E_{x}^{(4)} (z) = \frac{β_{4}}{i K_{0} n_{4}^{2}} D e x p (β_{4} z)$

The polarisation of the transmitted wave in the second medium is obtained from the Snell-Descartes law.

$\begin{matrix} d e (21) E_{x} = \frac{1}{i K_{0} n^{2}} \frac{\partial B_{y}}{\partial z} d e (20) i K_{0} B_{y} = (\frac{\partial E_{x}}{\partial z} - \frac{\partial E_{z}}{\partial x}) \end{matrix}$ $\begin{array}{l} d e (21) E_{x} = \frac{1}{i K_{0} n^{2}} \frac{\partial B_{y}}{\partial z} \\ d e (20) i K_{0} B_{y} = (\frac{\partial E_{x}}{\partial z} - \frac{\partial E_{z}}{\partial x}) \end{array}$

$\begin{matrix} i μ ε K_{0} E_{z} = - i K_{x} B_{y} E_{z} = - \frac{K_{x}}{K_{0} n^{2}} B_{y} \end{matrix}$ $\begin{array}{l} i μ ε K_{0} E_{z} = - i K_{x} B_{y} \\ E_{z} = - \frac{K_{x}}{K_{0} n^{2}} B_{y} \end{array}$

$B(1)y=Aexp(−iγ1z)+A\exp(iγ1z)$ $B_{y}^{(1)} = A e x p (- i γ_{1} z) + A^{\} e x p (i γ_{1} z)$

$B(2)y=Bexp(β2z)+B\exp(−β2z)$ $B_{y}^{(2)} = B e x p (β_{2} z) + B^{\} e x p (- β_{2} z)$

$B(3)y=Cexp(−iγ3z)+C\exp(iγ3z)$ $B_{y}^{(3)} = C e x p (- i γ_{3} z) + C^{\} e x p (i γ_{3} z)$

$B_{y}^{(4)} = D e x p (β_{4} z)$ $B_{y}^{(4)} = D e x p (β_{4} z)$

$y_{1}^{2} = n_{1}^{2} k_{0}^{2} {cos}^{2} θ$ $y_{1}^{2} = n_{1}^{2} k_{0}^{2} \cos^{2} θ$

$β_{2}^{2} = (n_{1}^{2} sin θ - n_{2}) K_{0}^{2}$ $β_{2}^{2} = (n_{1}^{2} \sin θ - n_{2}) K_{0}^{2}$

$y_{3}^{2} = (n_{3}^{2} - n_{1}^{2} si n^{2} θ) K_{0}^{2}$ $y_{3}^{2} = (n_{3}^{2} - n_{1}^{2} si n^{2} θ) K_{0}^{2}$

$β_{4}^{2} = (n_{1}^{2} {sin}^{2} θ - n_{4}^{2}) K_{0}^{2}$ $β_{4}^{2} = (n_{1}^{2} \sin^{2} θ - n_{4}^{2}) K_{0}^{2}$

$E_{x} = \frac{1}{i K_{0} n^{2}} \frac{\partial B_{y}}{\partial z}$ $E_{x} = \frac{1}{i K_{0} n^{2}} \frac{\partial B_{y}}{\partial z}$

$E(1)x(z)=γ1K0n21(−Aexp(−iγ1z)+A\exp(iγ1z))$ $E_{x}^{(1)} (z) = \frac{γ_{1}}{K_{0} n_{1}^{2}} (- A e x p (- i γ_{1} z) + A^{\} e x p (i γ_{1} z))$

$E(2)x(z)=β2iK0n22(Bexp(β2z)−B\exp(−β2z))$ $E_{x}^{(2)} (z) = \frac{β_{2}}{i K_{0} n_{2}^{2}} (B e x p (β_{2} z) - B^{\} e x p (- β_{2} z))$

$E(3)x(z)=γ3K0n23(−Cexp(−iγ3z)+C\exp(iγ3z))$ $E_{x}^{(3)} (z) = \frac{γ_{3}}{K_{0} n_{3}^{2}} (- C e x p (- i γ_{3} z) + C^{\} e x p (i γ_{3} z))$

$E_{x}^{(4)} (z) = \frac{β_{4}}{i K_{0} n_{4}^{2}} D e x p (β_{4} z)$ $E_{x}^{(4)} (z) = \frac{β_{4}}{i K_{0} n_{4}^{2}} D e x p (β_{4} z)$

We give the continuity equations in the multi-layer system:

$\to s . ({\to D}_{2} - {\to D}_{1}) = 0$ $\vec{s .} ({\vec{D}}_{2} - {\vec{D}}_{1}) = 0$

$n_{i}^{2} E_{i}^{1} (z) = n_{i + 1}^{2} E_{i + 1}^{1} (z)$ $n_{i}^{2} E_{i}^{1} (z) = n_{i + 1}^{2} E_{i + 1}^{1} (z)$

$\to s \times ({\to E}_{2} - {\to E}_{1}) = \to 0$ $\vec{s} \times ({\vec{E}}_{2} - {\vec{E}}_{1}) = \vec{0}$

$E_{x} (i) = E_{x} (i + 1) i = 1; 2; 3$ $E_{x}^{} (i) = E_{x}^{} (i + 1) i = 1; 2; 3$ at each interface.

$\to s \times ({\to H}_{2} - {\to H}_{1}) = \to 0$ $\vec{s} \times ({\vec{H}}_{2} - {\vec{H}}_{1}) = \vec{0}$

$B_{y}^{1} (d + a) = B_{y}^{2} (d + a)$ $B_{y}^{1} (d + a) = B_{y}^{2} (d + a)$

$E_{x}^{1} (d + a) = E_{x}^{2} (d + a)$ $E_{x}^{1} (d + a) = E_{x}^{2} (d + a)$

$B_{y}^{2} (d) = B_{y}^{3} (d)$ $B_{y}^{2} (d) = B_{y}^{3} (d)$

$E_{x}^{2} (d) = E_{x}^{3} (d)$ $E_{x}^{2} (d) = E_{x}^{3} (d)$

$B_{y}^{3} (- d) = B_{y}^{4} (- d)$ $B_{y}^{3} (- d) = B_{y}^{4} (- d)$

$E_{x}^{3} (- d) = E_{x}^{4} (- d)$ $E_{x}^{3} (- d) = E_{x}^{4} (- d)$

$n_{i}^{2} E_{z} (i) = n_{i + 1}^{2} E_{z} (i + 1)$ $n_{i}^{2} E_{z}^{} (i) = n_{i + 1}^{2} E_{z}^{} (i + 1)$

for i=1,2,3 for each interface in the multi-layer.

$A e x p (- i γ_{1} (d + a)) = - A {}^{‵}e x p (- i γ_{1} (d + a)) + B e x p (β_{2} (d + a)) + B {}^{‵}e x p (- β_{2} (d + a))$

$\frac{γ_{1}}{n_{1}^{2} K_{0}} A e x p (- i γ_{1} (d + a)) = \frac{γ_{1}}{n_{1}^{2} K_{0}} - A {}^{‵}e x p (- i γ_{1} (d + a)) - \frac{β_{2}}{i n_{1}^{2} K_{0}} [B e x p (β_{2} (d + a)) - B {}^{‵}e x p (- β_{2} (d + a))$

$0 = - B e x p (β_{2} d) - B^{\} e x p (- β_{2} d) + C e x p (- i γ_{3} d) + C^{\} e x p (i γ_{3} d)$

$0 = + \frac{β_{2}}{i n_{2}^{2} K_{0}} [B e x p (β_{2} d) - B^{\} e x p (- β_{2} d) + \frac{γ_{3}}{n_{3}^{2} K_{0}} [C e x p (- i γ_{3} d) - C^{\} e x p (i γ_{3} d)$

$0 = - C e x p (i γ_{3} d) + C^{\} e x p (- i γ_{3} d) + D e x p (- β_{4} d)$

$0 = \frac{β_{4}}{i K_{0}} B e x p (- β_{4} d) - \frac{γ_{3}}{n_{3}^{2} K_{0}} [C e x p (i γ_{3} d) - C^{\} e x p (- i γ_{3} d)$

We extract some factors from the matrix and call them I, II, III, IV, V, VI and VII:

$I = e x p (- i γ_{1} (d + a))$

$II = e x p (i γ_{1} (d + a))$

$III = e x p (β_{2} d)$

$IV = e x p (- β_{2} d)$

$V = e x p (- i γ_{3} d)$

$VI = e x p (i γ_{3} d)$

$VII = e x p (- β_{4} d)$

$\begin{array}{l} I_{1} = | \begin{array}{l} \end{array} \begin{matrix} 1 & - 1 & - 1 & 0 \\ \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & e x p (2 γ_{3} d) & e x p (- 2 γ_{3} d) & - 1 \\ 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 γ_{3} d) & \frac{- γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix} \begin{array}{l} \end{array} | \\ I_{2} = | \begin{array}{l} \end{array} \begin{matrix} 1 & - 1 & - 1 & 0 \\ - \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & e x p (2 γ_{3} d) & e x p (- 2 γ_{3} d) & - 1 \\ 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 γ_{3} d) & \frac{- γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix} \begin{array}{l} \end{array} | \end{array}$

$I_{1} = \frac{2 i}{K_{0}^{2}} [\frac{γ_{3}}{n_{3}^{2}} (\frac{β_{2}}{n_{2}^{2}} + β_{4}) c o s (2 γ_{3} d) - (\frac{γ_{3}^{2}}{n_{3}^{4}} - \frac{β_{2} β_{4}}{n_{2}^{2}}) s i n (2 γ_{3} d)]$

$I_{2} = \frac{2 i}{K_{0}^{2}} [\frac{γ_{3}}{n_{3}^{2}} (- \frac{β_{2}}{n_{2}^{2}} + β_{4}) c o s (2 γ_{3} d) - (\frac{γ_{3}^{2}}{n_{3}^{4}} + \frac{β_{2} β_{4}}{n_{2}^{2}}) s i n (2 γ_{3} d)]$

$X = \frac{γ_{3}}{n_{3}^{2}} (\frac{β_{2}}{n_{2}^{2}} + β_{4}) c o s 2 γ_{3} d - (\frac{γ_{3}^{2}}{n_{3}^{4}} - \frac{β_{2} β_{4}}{n_{2}^{2}}) s i n 2 γ_{3} d$

$Y = \frac{γ_{3}}{n_{3}^{2}} (- \frac{β_{2}}{n_{2}^{2}} + β_{4}) c o s 2 γ_{3} d - (\frac{γ_{3}^{2}}{n_{3}^{4}} + \frac{β_{2} β_{4}}{n_{2}^{2}}) s i n 2 γ_{3} d$

$d e t A = \frac{2}{K_{0}^{3}} (G + i H)$ $d e t A = \frac{2}{K_{0}^{3}} (G + i H)$

$d e t A = \frac{2}{K_{0}^{3}} (G + i H) e x p (i γ_{3} (d + a)) e x p (- β_{4} d)$

With: $G= \frac{β_{2}}{n_{2}^{2}} (X e x p (β_{2} a) + Y e x p (- β_{2} a))$

$H= \frac{γ_{1}}{n_{1}^{2}} (- X e x p (β_{2} a) + Y e x p (- β_{2} a))$

$(\begin{matrix} - 1 & - e x p (β_{2} a) & - e x p (- β_{2} a) & 0 & 0 & 0 \\ \frac{- γ_{1}}{n_{1}^{2} K_{0}} & \frac{β_{2}}{i n_{2}^{2} K_{0}} e x p (β_{2} a) & \frac{- β_{2}}{i n_{2}^{2} K_{0}} e x p (- β_{2} a) & 0 & 0 & 0 \\ 0 & 1 & 1 & - 1 & - 1 & 0 \\ 0 & \frac{- β_{2}}{i n_{2}^{2} K_{0}} & \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & 0 & 0 & e x p (2 i γ_{3} d) & e x p (- 2 i γ_{3} d) & - 1 \\ 0 & 0 & 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 i γ_{3} d) & - \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 i γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix})$

$\begin{array}{l} d e t A^{\} = - \frac{β_{2}}{i n_{2}^{2} K_{0}} e x p (β_{2} a) | \begin{array}{l} \end{array} \begin{matrix} 1 & - 1 & - 1 & 0 \\ \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & e x p (2 γ_{3} d) & e x p (- 2 γ_{3} d) & - 1 \\ 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 γ_{3} d) & \frac{- γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix} \begin{array}{l} \end{array} | \\ - \frac{β_{2}}{i n_{2}^{2} K_{0}} e x p (- β_{2} a) | \begin{array}{l} \end{array} \begin{matrix} 1 & - 1 & - 1 & 0 \\ - \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & e x p (2 γ_{3} d) & e x p (- 2 γ_{3} d) & - 1 \\ 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 γ_{3} d) & \frac{- γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix} \begin{array}{l} \end{array} | \end{array}$

$\begin{array}{l} - \frac{γ_{1}}{n_{1}^{2} K_{0}} e x p (β_{2} a) | \begin{array}{l} \end{array} \begin{matrix} 1 & - 1 & - 1 & 0 \\ \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & e x p (2 γ_{3} d) & e x p (- 2 γ_{3} d) & - 1 \\ 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 γ_{3} d) & \frac{- γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix} \begin{array}{l} \end{array} | \\ + \frac{γ_{1}}{n_{1}^{2} K_{0}} e x p (- β_{2} a) | \begin{array}{l} \end{array} \begin{matrix} 1 & - 1 & - 1 & 0 \\ - \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & e x p (2 γ_{3} d) & e x p (- 2 γ_{3} d) & - 1 \\ 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 γ_{3} d) & \frac{- γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix} \begin{array}{l} \end{array} | \end{array}$

$d e t A^{\} = - (\frac{β_{2}}{i n_{2}^{2} K_{0}} + \frac{γ_{1}}{n_{1}^{2} K_{0}}) e x p (β_{2} a) I_{1} - (\frac{β_{2}}{i n_{2}^{2} K_{0}} - \frac{γ_{1}}{n_{1}^{2} K_{0}}) e x p (- β_{2} a) I_{2}$

$d e t A^{\} = - \frac{2}{K_{0}^{3}} (G - i H) e x p (- i γ_{3} (d + a)) e x p (- β_{4} d)$

$j = \frac{2}{K_{0}^{3}} e x p (- i γ_{3} (d + a)) e x p (- β_{4} d)$

$d e t A = j(G+iH)$

: j^* is the conjugate of j

$d e t A^{\} = - j^{*} (G-iH)$

$(\begin{matrix} 1 & - 1 & - e x p (- β_{2} a) & 0 & 0 & 0 \\ \frac{- γ_{1}}{n_{1}^{2} K_{0}} & \frac{- γ_{1}}{n_{1}^{2} K_{0}} & \frac{- β_{2}}{i n_{2}^{2} K_{0}} e x p (- β_{2} a) & 0 & 0 & 0 \\ 0 & 0 & 1 & - 1 & - 1 & 0 \\ 0 & 0 & \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & 0 & 0 & e x p (2 i γ_{3} d) & e x p (- 2 i γ_{3} d) & - 1 \\ 0 & 0 & 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 i γ_{3} d) & - \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 i γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix})$

$d e t B = - \frac{2 γ_{1}}{n_{1}^{2} K_{0}} I_{1}$ with $I_{1} = \frac{2 i}{K_{0}^{2}} X$

$d e t B = - 4 \frac{i γ_{1}}{n_{1}^{2} K_{0}^{3}} X e x p (- d (β_{2} + β_{4}))$

$(\begin{matrix} 1 & - e x p (β_{2} a) & - 1 & 0 & 0 & 0 \\ \frac{- γ_{1}}{n_{1}^{2} K_{0}} & \frac{β_{2}}{i n_{2}^{2} K_{0}} e x p (β_{2} a) & \frac{- γ_{1}}{n_{1}^{2} K_{0}} & 0 & 0 & 0 \\ 0 & 1 & 0 & - 1 & - 1 & 0 \\ 0 & \frac{- β_{2}}{i n_{2}^{2} K_{0}} & 0 & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & 0 & 0 & e x p (2 i γ_{3} d) & e x p (- 2 i γ_{3} d) & - 1 \\ 0 & 0 & 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 i γ_{3} d) & - \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 i γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix})$

$d e t B^{\} = \frac{2 γ_{1}}{n_{1}^{2} K_{0}} I_{2}$ with $I_{2} = \frac{2 i}{K_{0}^{2}} Y$

$d e t B^{\} = 4 \frac{i γ_{1}}{n_{1}^{2} K_{0}^{3}} Y e x p (d (β_{2} - β_{4}))$

$(\begin{matrix} 1 & - e x p (β_{2} a) & - e x p (- β_{2} a) & - 1 & 0 & 0 \\ \frac{- γ_{1}}{n_{1}^{2} K_{0}} & \frac{β_{2}}{i n_{2}^{2} K_{0}} e x p (β_{2} a) & \frac{- β_{2}}{i n_{2}^{2} K_{0}} e x p (- β_{2} a) & \frac{- γ_{1}}{n_{1}^{2} K_{0}} & 0 & 0 \\ 0 & 1 & 1 & 0 & - 1 & 0 \\ 0 & \frac{- β_{2}}{i n_{2}^{2} K_{0}} & \frac{β_{2}}{i n_{2}^{2} K_{0}} & 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} & 0 \\ 0 & 0 & 0 & 0 & e x p (- 2 i γ_{3} d) & - 1 \\ 0 & 0 & 0 & 0 & - \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (- 2 i γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix})$

$d e t C = \frac{2 β_{2} γ_{1}}{i n_{2}^{2} n_{1}^{2} K_{0}^{2}} | \begin{matrix} - \frac{γ_{1}}{K_{0}} & 0 & 0 \\ 0 & e x p (- 2 γ_{3} d) & - 1 \\ 0 & - \frac{γ_{3}}{K_{0}} e x p (- 2 γ_{3} d) & \frac{β_{4}}{i K_{0}} \end{matrix} |$

$d e t C = \frac{4 β_{2} γ_{1}}{n_{1}^{2} n_{2}^{2} K_{0}^{3}} (β_{4} - i \frac{γ_{3}}{n_{3}^{2}}) e x p (- 2 i γ_{3} d)$

$d e t C = \frac{4 β_{2} γ_{1}}{n_{1}^{2} n_{2}^{2} K_{0}^{3}} (β_{4} - i \frac{γ_{3}}{n_{3}^{2}}) e x p (- 2 i γ_{3} d) e x p (- β_{4} d)$

$(\begin{matrix} 1 & - e x p (β_{2} a) & - e x p (- β_{2} a) & 0 & - 1 & 0 \\ \frac{- γ_{1}}{n_{1}^{1} K_{0}} & \frac{β_{2}}{i n_{2}^{2} K_{0}} e x p (β_{2} a) & \frac{- β_{2}}{i n_{2}^{2} K_{0}} e x p (- β_{2} a) & 0 & \frac{- γ_{1}}{n_{1}^{2} K_{0}} & 0 \\ 0 & 1 & 1 & - 1 & 0 & 0 \\ 0 & \frac{- β_{2}}{i n_{2}^{2} K_{0}} & \frac{β_{2}}{i n_{2}^{2} K_{0}} & \frac{- γ_{3}}{n_{3}^{2} K_{0}} & 0 & 0 \\ 0 & 0 & 0 & e x p (2 i γ_{3} d) & 0 & - 1 \\ 0 & 0 & 0 & \frac{γ_{3}}{n_{3}^{2} K_{0}} e x p (2 i γ_{3} d) & 0 & \frac{β_{4}}{i K_{0}} \end{matrix})$

$d e t C^{\} = - \frac{4 β_{2} γ_{1}}{i n_{1}^{2} n_{2}^{2} K_{0}^{3}} (β_{4} + i \frac{γ_{3}}{n_{3}^{2}}) e x p (2 i γ_{3} d)$

$d e t C^{\} = - \frac{4 β_{2} γ_{1}}{i n_{1}^{2} n_{2}^{2} K_{0}^{3}} (β_{4} + i \frac{γ_{3}}{n_{3}^{2}}) e x p (2 i γ_{3} d) e x p (- β_{4} d)$

$(\begin{matrix} 1 & - e x p (β_{2} a) & - e x p (- β_{2} a) & 0 & 0 & - 1 \\ \frac{- γ_{1}}{K_{0}} & \frac{β_{2}}{i K_{0}} e x p (β_{2} a) & \frac{- β_{2}}{i K_{0}} e x p (- β_{2} a) & 0 & 0 & \frac{- γ_{1}}{K_{0}} \\ 0 & 1 & 1 & - 1 & - 1 & 0 \\ 0 & \frac{- β_{2}}{i K_{0}} & \frac{β_{2}}{i K_{0}} & \frac{- γ_{3}}{K_{0}} & \frac{γ_{3}}{K_{0}} & 0 \\ 0 & 0 & 0 & e x p (2 i γ_{3} d) & e x p (- 2 i γ_{3} d) & 0 \\ 0 & 0 & 0 & \frac{γ_{3}}{K_{0}} e x p (2 i γ_{3} d) & - \frac{γ_{3}}{K_{0}} e x p (- 2 i γ_{3} d) & 0 \end{matrix})$

$d e t D = \frac{- 8 i γ_{1} γ_{3} β_{2}}{K_{0}^{3}}$

The coefficients $A, A^{\}, B, B^{\}, C, C^{\}, D$ are given by the following relationship:

$\frac{A}{d e t A} = \frac{A^{\}}{d e t A^{\}} = \frac{B}{d e t B} = \frac{B^{\}}{d e t B^{\}} = \frac{C}{d e t C} = \frac{C^{\}}{d e t C^{\}} = \frac{D}{d e t D}$

$A^{\} = - A \frac{j^{*} (G - i H)}{j (G + i H)}$

$B = - A \frac{4 i γ_{1} X}{K_{0}^{3} J (G + i H)} e x p (- d (β_{2} + β_{4}))$

$B^{\} = A \frac{4 i γ_{1} Y}{K_{0}^{3} J (G + i H)} e x p (- d (β_{2} - β_{4}))$

$C = A \frac{4 β_{2} γ_{1}}{K_{0}^{3} J (G + i H)} (β_{4} - i γ_{3}) e x p (- d β_{4}) e x p (- i γ_{3} d)$

$C^{\} = - A \frac{4 β_{2} γ_{1}}{K_{0}^{3} J (G + i H)} (β_{4} + i γ_{3}) e x p (- d β_{4}) e x p (i γ_{3} d)$

$D = - A \frac{8 i γ_{1} γ_{3} β_{2}}{K_{0}^{3} j (G + i H)}$

Results:

We take an incidence angle close to the critical angle (optimum of transmission in the TE mode). See reference.¹

$θ_{i n c}$ =52⁰

${\begin{cases} E_{x} = \frac{1}{i K_{0} n^{2}} \frac{\partial B_{y}}{\partial z} \\ E_{z} = - \frac{K_{x}}{K_{0} n^{2}} B_{y} \end{cases}$

${\vec{E}}_{T} = E_{x} \vec{i} + E_{z} \vec{k}$

${\vec{E}}_{T} (4) = E_{x} (4) \vec{i} + E_{z} (4) \vec{k}$

${\vec{E}}_{T} = \frac{β_{4}}{i K_{0} n^{4}} D e x p (β_{4} z) \vec{i} - \frac{K_{x}}{K_{0} n^{4}} D e x p (β_{4} z) \vec{k}$

${\vec{E}}_{T} (4) . c o n j ({\vec{E}}_{T} (4)) = {| D |}^{2} \exp (2 β_{4} z)$

${\vec{E}}_{T} (1) = \frac{γ_{1}}{K_{0} n_{1}^{2}} (- A e x p (- i γ_{1} z) + A ` e x p (i γ_{1} z)) \vec{i} - \frac{K_{x}}{K_{0} n_{1}^{2}} (A e x p (- i γ_{1} z) + A ` e x p (i γ_{1} z)) \vec{k}$

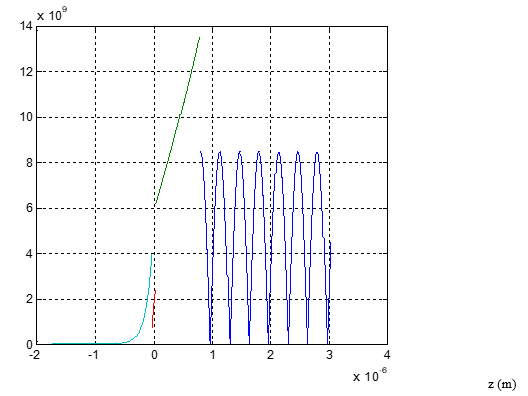
Figure 2 The perpendicular component EZ of the electric field (V/m).

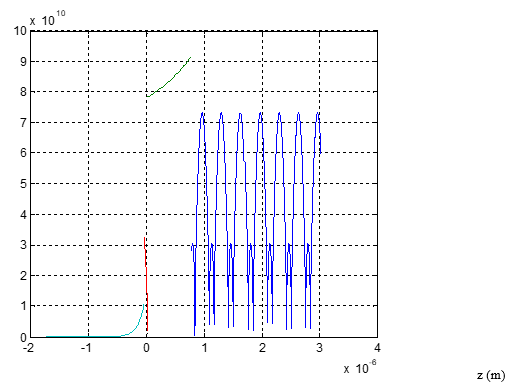
Figure 3 The parallel component EX of the electric field (V/m).

${\begin{cases} E_{x} = \frac{1}{i K_{0} n^{2}} \frac{\partial B_{y}}{\partial z} \\ E_{z} = - \frac{K_{x}}{K_{0} n^{2}} B_{y} \end{cases}$

${\vec{E}}_{T} = E_{x} \vec{i} + E_{z} \vec{k}$

${\vec{E}}_{T} (4) = E_{x} (4) \vec{i} + E_{z} (4) \vec{k}$

${\vec{E}}_{T} = \frac{β_{4}}{i K_{0} n^{4}} D e x p (β_{4} z) \vec{i} - \frac{K_{x}}{K_{0} n^{4}} D e x p (β_{4} z) \vec{k}$

${\vec{E}}_{T} (4) . c o n j ({\vec{E}}_{T} (4)) = {| D |}^{2} \exp (2 β_{4} z)$

${\vec{E}}_{T} (1) . c o n j ({\vec{E}}_{T} (1)) = \frac{| {A |}^{2}}{n_{1}^{4}}$

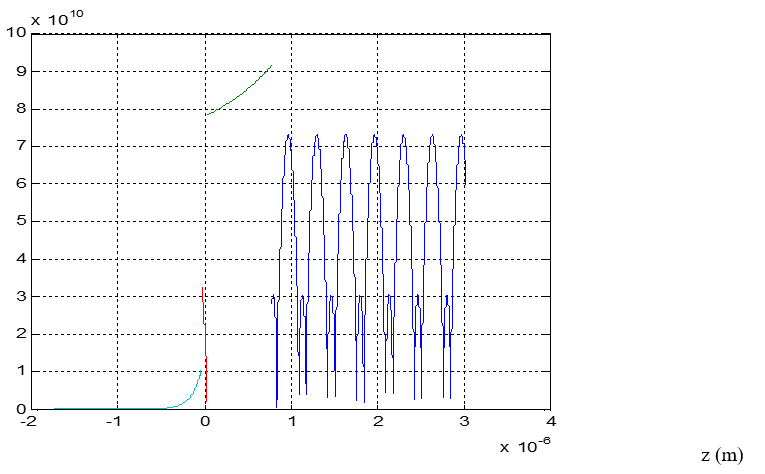
Figure 4 The total electric field ET in the atomic mirror function of the transverse coordinate z.

We notice that the electric field is bigger in the gap and then decreases in the vaccum where it is smaller than in the prism.

The transmission factor is given by:⁴

$T = {| \frac{{\vec{E}}_{T} (4) z = - d}{{\vec{E}}_{T} (1) z = d + a} |}^{2} = \frac{{\vec{E}}_{T} (4) . c o n j ({\vec{E}}_{T} (4)) z = - d}{{\vec{E}}_{T} (1) . c o n j ({\vec{E}}_{T} (1)) z = d + a}$

$T = \frac{{(4 γ_{1} γ_{3} β_{2})}^{2}}{n_{2}^{2} n_{3}^{2} (G^{2} + H^{2})}$

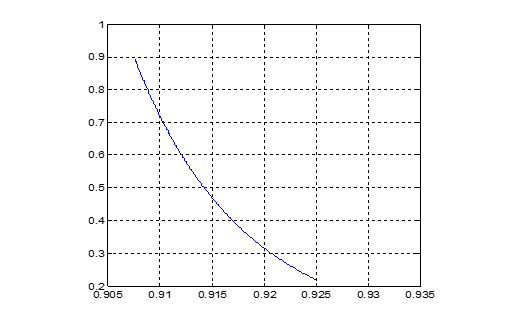
Figure 5 The transmission factor in the atomic mirror.

We conclude that there is no enhancement in the vaccum for the electric field and there is no technological progress or advantage for this kind of excitation.^1,5-7