In this paper we have considered here that the DNA molecule can be treated as a spin system when spins are located on the axis forming an antiferromagnetic chain. When spins are described in the Lie algebra of $SU\left(2\right)$  the linking number can be ascertained from the Chern-Simons topology associated with the spin system. It is shown that bend and twist are not two separate entities but one depends on the other, also other hand entanglement of two DNA molecule inserting spin-echo to one of them marks the transform of Berry phase that can be exact as a calculate of entanglement. This formalism helps us to depict the thermodynamic entropy as entanglement entropy and the entanglement of spin can be used as a resource for genetic information and the transcription of genetic information can be considered in the framework of quantum information theory.

Keywords: DNA molecule, spin system, antiferromagnetic chain, Chern-Simons topology, berry phase, genetic information, quantum information theory

It is now well known that DNA can be regarded as a physical elastic object in a viscous environment. Two strands of double helix are antiparallel and two polynucleotide chains are coiled about the same axis such that B-DNA (Z-DNA) has right-handed (left-handed) helical sense. The existence of supercoiled DNA has been confirmed in experiments long ago and it was found that in vivo chromosomal DNA molecules contain topological domains along which supercoiling can occur.^1–3 DNA molecules from prokaryotes (cells without nuclear membranes) often adopt the interwound structures which are called “plectonemic” supercoils. In eukaryotes (cells with nuclei and other organelles with their own internal membranes) chromosomal DNA molecules are also known to be organized into topological independent loops.^2–5 Statistical mechanics of supercoiled DNA has been studied by several authors.⁶ The experiments of Boles et al.⁷ suggest that thermal fluctuations determine the structure of supercoils. Experiments of Bednar et al.⁸ indicated that DNA-DNA attraction may compete with fluctuation entropy. In this note we shall study different statistical mechanical aspects of DNA supercoils by taking into consideration that a DNA supercoil can be viewed as a chain of spin system. In fact as two polynucleotide chains are coiled about the same axis with a specific helical sense in a DNA molecule, we may visualize it such that a spin with a specific orientation is inserted on the axis in the coil such that two adjacent coils have opposite orientations of the spin. This follows from the fact that with each turn two strands move in the opposite side of the axis and so the spin orientations assigned for two adjacent coils should be opposite to each other.

In view of this a DNA supercoil may be considered to represent an antiferromagnetic chain of spins located on the axis of the supercoil. We shall study the topological properties as well as the elastic and thermodynamical properties of a DNA supercoil from an analysis of this spin system. Indeed, the topological property such as the linking number can be derived from the Chern-Simons topology associated with a quantum spin.^9,10 The elastic properties such as bending (curvature) and twisting (torsion) can be formulated in terms of gauge fields when spins are transcribed as gauge currents.^9,10 The added bonus in this formulation is that it directly indicates the interdependence of bending and twisting. The thermodynamical entropy associated with a DNA supercoil appears here as the entanglement entropy of the antiferromagnetic spin chain. It may be pointed out that entanglement entropy of a DNA supercoil essentially represents the total amount of information that can be transcribed. Thus we arrive at a quantitative description of the genetic information contained in the supercoil and the process of genetic information transcription can be visualized in the framework of quantum information theory. Also we shall show that DNA loops in the supercoil appear as topological objects like solutions (skyrmions). In Sec. 2 we shall formulate DNA supercoil as a spin chain. In Sec.3 we shall study the topological property of a DNA supercoil from the perspective of such a spin chain .In Sec.4 we shall formulate the elastic properties and in see. 5 we shall compute the entanglement entropy of the supercoil .In Sec.6 we shall show that DNA loops can be viewed as topological objects like solutions in this formulism. In Sec.7 we shall study the entanglement of two DNA molecule inserting spin-echo to one of them marks the transform of Berry phase that can be exact as a calculate of entanglement.

DNA as a polynucleotide spin manacles system

We consider that as two polynucleotide chains are coiled about the same axis with a specific helical sense in a DNA molecule, this can be viewed as if a spin with a specific orientation is inserted on the axis of the coil such that two adjacent coils have opposite orientations of the spin. In fact with each turn two strands move in the opposite side of the axis and so the spin orientation assigned for the two adjacent coils should be opposite to each other. Thus a DNA supercoil may be viewed as a long chain of an antiferromagnetic spin system when the spin is considered to be located on the axis of the supercoil. A unit vector depicting the tangent $\overrightarrow{t}={\partial }_s\overrightarrow{r}$ where $\overrightarrow{r}(s)$ is a space curve parameterized by the arc length s can be associated with a spin vector when the spin is located at the spatial point x on the axis. A spin vector in the Lie algebra of $SU\left(2\right)$  representation can be constructed with bosonic or fermionic oscillators. We write the spin vector $\overrightarrow{S}(x)$  as

$\overrightarrow{S}(x)={\psi }_{\alpha }^{\text{†}}\left(x\right){\overrightarrow{\sigma }}_{\alpha \beta }{\psi }_{\beta }\left(x\right)$ (1)

where ${\psi }^{\text{†}}\left(\psi \right)$ is the fermionic oscillator function and ${\overrightarrow{\sigma }}_{\alpha \beta }$  is the vector of Pauli matrices. A unit vector$\overrightarrow{n}$ is constructed as  

$\overrightarrow{n}=\left({\psi }_1^{*}{\psi }_2^{*}\right)\overrightarrow{\sigma }\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\end{array}\right)$ (2)

 with ${\psi }_1=\left(\cos \raisebox{1ex}{${\displaystyle \theta }$}\!\left/ \!\raisebox{-1ex}{${\displaystyle 2}$}\right.\right)e^{\raisebox{1ex}{${\displaystyle i\varphi }$}\!\left/ \!\raisebox{-1ex}{${\displaystyle 2}$}\right.}$ (3.a)

${\psi }_2=\left(\sin \raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)e^{\raisebox{1ex}{$-i\varphi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$  (3.b)

We now will study the appearance of Berry phase in the entanglement of two identical spin $1/2$ quantized particles. The antisymmetric Bell State of two spin $1/2$ DNA molecules is

$\left|{\psi }_2\right.〉=\cos \theta \left|{\psi }_1\right.〉=\frac{1}{2\pi }({\Delta }^{up}-{\Delta }^{down})\left|{\psi }_1\right.〉$  (3.c)

By the difference of Berry phase factor.

The most general antisymmetric Bell state for two particles A and B situated at the points x and y becomes

$\left|{\psi }_2(t)\right.〉=(\left.\alpha \right|\uparrow (t)\rangle \left|\downarrow (t)\rangle -\left.\beta \right|\uparrow (t)\rangle \left|\downarrow (t)\rangle \right.\right.$ (3.d)

Where $\alpha$  and $\beta$  are two complex coefficients,

With the idea of one DNA molecule rotation of one fermion for a time interval $\tau$  the spinor comes to its orginal state acquiring only Berry phase and loosing the dynamical phase. , We have the new form of the entangle state as

$\left|{\psi }_2(t=\tau )\right.〉=(\left.\alpha \right|\uparrow (t)\rangle \left|\downarrow (t)\rangle -e^{2i{\Delta }^{up}}\left|\uparrow (t)\right.\rangle \beta \left|\downarrow (t)\rangle \right.\right.$ (3.e)

As we consider $\theta =\pi$  the Berry phase is removed along with dynamical phase in the ’spin-echo’ method.

This helps us to write

$\overrightarrow{S}(x)=\left(\sqrt{3}/2\right){\psi }_{\alpha }^{\text{†}}\left(x\right){\overrightarrow{\sigma }}_{\alpha \beta }^{}{\psi }_{\beta }$ (4)

We can now construct a unit vector $n_{\mu }$  with $\mu =0,1,2,3$  in 3+1 dimensions incorporating the unit vector $\overrightarrow{n}$  given by eqn. (2)

$n_{\mu }=\left(1/\sqrt{2}\right)\left({\psi }_1^{*}{\psi }_2^{*}\right){\sigma }_{\mu }\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\end{array}\right)$ (5)

with ${\sigma }_0=\text{I}$ , I being the identity matrix and $\overrightarrow{\sigma }$  are Pauli matrices. We now construct the topological current

$J_{\mu }=\left(1/12{\pi }^2\right){\epsilon }_{\mu \nu \lambda \sigma }{\epsilon }_{abcd}{n}_a{\partial }_{\nu }{n}_b{\partial }_{\lambda }{n}_c{\partial }_{\sigma }{n}_d$ (6)

where (a, b, c, d) correspond to (0, 1, 2, 3) and $\left(\mu ,\nu ,\lambda ,\sigma \right)$  correspond to space-time indices. The current $J_{\mu }$ can be written in the form11

$J_{\mu }=\left(1/24{\pi }^2\right){\epsilon }_{\mu \nu \lambda \sigma }Tr(g^{-1}{\partial }_{\nu }g)(g^{-1}{\partial }_{\lambda }g)(g^{-1}{\partial }_{\sigma }g)$   (7)

with $g=n_0\text{I }+i\text{.}\overrightarrow{\sigma }$  which belongs to the group $SU\left(2\right)$ . If we now demand that in Euclidean 4- dimensional space-time the field strength $F_{\mu \nu }$ of a gauge potential $A_{\mu }$  vanishes at all points on the boundary $S^3$ of a certain volume $V^4$ inside which $F_{\mu \nu }\ne 0$ the gauge potential tends to a pure gauge towards the boundary and we write

$A_{\mu }=g^{-1}{\partial }_{\mu }g$ (8)

with $g\epsilon SU\left(2\right)$ .

We can now write the topological current given by (7) as¹⁰

$J_{\mu }=\left(1/16{\pi }^2\right){\epsilon }^{\mu \nu \lambda \sigma }Tr\left\{A_{\nu }{F}_{\lambda \sigma }+\left(2/3\right)A_{\nu }{A}_{\lambda }{A}_{\sigma }\right\}$ (9)

with $A_{\mu }$  given by eqn.(8) .It is noted that as the spin vector is constructed from the unit vector $\overrightarrow{n}$ given by (2) which is incorporated in the current $J_{\mu }$ as is evident from eqn. (6), we can associate spin with this current $J_{\mu }$ .In fact we can consider the topological Lagrangian in terms of the $SU\left(2\right)$ gauge fields in affine spece

$L=-\left(1/4\right)Tr{\epsilon }^{{}_{\mu \nu \alpha \beta }}{F}_{\mu \nu }{F}_{\alpha \beta }$ (10.a)

Now the gauge connection associated with the Lagrangian in this equation $L_{eff}^{up}=-(i/2)($ $\dot{\xi }-$ $\dot{\varphi }\mathrm{Cos}\theta )$ (10.b)

due to any change in $\theta$  ,$\varphi$ ,$\xi$  resulting a gauge transformation, this equation giving rise to Berry phase.

Now the necessary geometrical phase of the only quantized spinor

${\Delta }^{up}=i{\displaystyle \int L_{eff}^{up}dt=i{\displaystyle \oint A^{up}(\lambda )d\lambda =(1/2)({\displaystyle \oint d\xi -\cos \theta {\displaystyle \oint d\varphi )=\pi (1-\cos \theta )}}}}$ (10.c)

This gives rise to the topological current¹²

$\overrightarrow{J_{\mu }}={\epsilon }^{\mu \nu \lambda \sigma }{\overrightarrow{a}}_{\nu }\times {\overrightarrow{f}}_{\lambda \sigma }={\epsilon }^{\mu \nu \lambda \sigma }{\partial }_{\nu }{\overrightarrow{f}}_{\lambda \sigma }$ (11)

where we have taken the $SU\left(2\right)$  gauge field $A_{\mu }$ and corresponding field strength $F_{\mu \nu }$ as

 $A_{\mu }=\overrightarrow{a_{\mu }}.\overrightarrow{\sigma }$  and $F_{\mu \nu }=\overrightarrow{f_{\mu \nu }}.\overrightarrow{\sigma }$  (12)

$\overrightarrow{\sigma }$ being vector of Pauli matrices. From this it appears that the spin vector $\overrightarrow{S}(x)$ can be depicted as the topological current $\overrightarrow{J_{\mu }}$ given by eqn. (11). In terms of this current a spin system on a lattice can be viewed as if currents are located on the vertices when gauge fields lie on links.⁹ This helps us to consider the spin system associated with a DNA supercoil in terms of the Chern-Simons topology as will be discussed in the next section.

DNA molecule is organized into topological properties

In length scales of a large number of base pairs DNA in vivo is organized into topologically independent loops. The two strands of a circular DNA molecule possess as a topological invariant the number of times they wind around each other which is known as the linking number. A B-DNA molecule has one right-handed twist per $h=3.4$ nm along its length. When these are closed in a planar circle without twisting of the ends the resulting linking number is $L{k}_o=L/h={\omega }_{0}L/\left(2\pi \right)$  where $L$  is the length and ${\omega }_0$  is the spatial rotation rate of the base pairs about the central axis. Deviations in the twisting rate from ${\omega }_0$ is measured relative to $L{k}_o$ through the parameter defining the excess linking $\sigma =\left(\Delta Lk/L{k}_0\right)$ where $\Delta Lk=Lk-L{k}_0$ .The linking number $Lk$  is expressed as $Lk=Tw+Wr$  where $Tw$  represents the twist corresponding to the rotation of the internal degrees of freedom about the molecule axis and $Wr$  represents the writhe.^13,14 The twist measures the winding of one curve about the other. It can be mathematically expressed as⁶

 $Tw={\displaystyle \underset{0}{\overset{L}{\int }}\left(ds/2\pi \right)}\left[{\omega }_0+\Omega \left(s\right)\right]=L{k}_o+\Delta Tw$  (13) where Ω is the twist strain measuring the excess or deficit rotation of the base pairs about the axis and $s$  defines the arc length. The Writhe characterizes the chiral deformation of a curve. One can assign an orientation to a curve and compute the sum of signed crossings in a planar projection along every direction. $Wr$ is equal to the average of such sums over all projections.¹⁵ For a configuration $\overrightarrow{r}\left(s\right)$  depicting a space curve parameterized by arc length $s$ , we define the tangent vector $\overrightarrow{t}={\partial }_s\overrightarrow{r}$ which traces out a closed path on the unit sphere. The writhe is equal to the total area A on the unit sphere enclosed by the path divided by $2\pi$ .¹⁶

$Wr=A/2\pi$ (14)

Right-handed and left-handed circulation on the sphere contribute positively and negatively respectively to $A$ . The length of a molecule in 1 rad of the superhelix is $l=\sqrt{R^2+P^2}$  where $R\left(P\right)$  represents the radius (pitch) of the superhelix, the helix repeat length being $2\pi P$ . The helix angle $\gamma$  is defined by $\sin \gamma =\raisebox{1ex}{$P$}\!\left/ \!\raisebox{-1ex}{$l$}\right.$ .$\gamma$  takes values between 0 and $\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$  where $\gamma =0\left(\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$  corresponds to circle (straight line). A solenoidal superhelix represents a toroidal structure. For B-DNA a plectonemic superhelix consists of two right-handed helices that are interwound. At the end of the resulting cylindrical structure, the two helices are connected. The writhes of plectonemic and solonoidal coils are¹⁴

$Wr=\left\{\begin{array}{c}\mp 2n\sin \gamma \\ \pm n\left(1-\sin \gamma \right)\end{array}\right.$$\begin{array}{c}\text{( plectoneme)}\\ \text{(solenoid)}\end{array}$ (15)

where $n$ is the number of superhelix repeats given by $n=L/4\pi l$ for the plectoneme and $n=L/2\pi l$ for the solenoid. The upper (lower) sign corresponds to the value for right (left-handed) supercoil. From the point of view that a DNA supercoil can be depicted as a spin system we can determine the linking number from the spin degrees of freedom . It is noted that the expression of the current $\stackrel{}{J_{\mu }}$ associated with the spin given by eqn. (9) essentially corresponds to the Chern-Simons secondary characteristics class . The topological charge

$q={\displaystyle \int J_0{d}^{3}x}$ (16)

corresponds to the winding number associated with the homotopy ${\pi }_3(S^3)=Z$ and can be written as

$q=2\mu =\left(1/24{\pi }^2\right){\displaystyle \underset{S^3}{\int }{\epsilon }^{\mu \nu \lambda \sigma }Tr(g^{-1}{\partial }_{\nu }g)(g^{-1}{\partial }_{\lambda }g)(g^{-1}{\partial }_{\sigma }g)}$ (17)

This charge $q$  essentially represents the Pontryagin index which is an integer and the relation $q=2\mu$  implies that $\mu$  corresponds to the magnetic monopole strength and can take the value $\mu =0,\pm 1/2,\pm 1,\pm 3/2$ .

This Pontryagin index can be written as the integral in the 4-dimensional manifold $M_4$ as

$q={\displaystyle \underset{M_4}{\int }Tr(F\wedge F)}$ (18)

where $F$ is the two-form related to the field strength associated with the $SU\left(2\right)$ gauge field $A_{\mu }$ .Now from the relation

${\displaystyle \underset{M_4}{\int }Tr(F\wedge F)}={\displaystyle \underset{M_4}{\int }Tr(A\wedge dA}+\left(2/3\right)A\wedge A\wedge A)$ (19)

where $M_3$ is a three dimensional manifold and $A$ is the one-form corresponding to the $SU\left(2\right)$  gauge field $A_{\mu }$  we note that the R.H.S of eqn.(19) represents the Chern-Simons invariant and is thus found to be associated with the Pontryagin index. Noting that the Pontryagin index corresponding to the charge related to the gauge current $\stackrel{}{J_{\mu }}$ given by eqn.(9) which is associated with the spin , we can consider spin in the framework of Chern-Simons topology .In fact from eqn.(11) we note that any component of the spin vector can be written as

$J_{\mu }^a(a=1,2,3)={\epsilon }^{\mu \nu \lambda \sigma }{a}_{\nu }{\partial }_{\lambda }{a}_{\sigma }$ (20)

where $a_{\nu }$ corresponds to an Abelian gauge field . When we project it onto a three dimensional manifold this corresponds to the Chern-Simons term ${\epsilon }^{\nu \lambda \sigma }{a}_{\nu }{\partial }_{\lambda }{a}_{\sigma }$ .In the Abelian theory we consider the one-form $a$ associated with the gauge field $a_{\nu }$  and choose the action

$S=\left(k/8\pi \right){\displaystyle \underset{M_3}{\int }{\epsilon }^{ijk}}{a}_i{\partial }_j{a}_k$ (21)

where $k$ is an integer. We now pick up some circles $C_a$  and some integers $n_a$ corresponding to representations of the Abelian gauge group. It is assumed that two curve $C_a$ and $C_l$ do not intersect for $a\ne b$ . As shown by Polyakorv17 the expectation value of the product

$W={\displaystyle \prod \exp (i{n}_a{\displaystyle \underset{C_a}{\int }a}}$ (22)

with respect to the measure determined by $e^{iS}$ is given by

$〈W〉=\exp \left(\left(i/2k\right){\displaystyle \sum _{a,b}{n}_a{n}_b{\displaystyle \underset{C_a}{\int }d{x}^i{\displaystyle \underset{C_b}{\int }d{y}^j}}{\epsilon }_{ijk}\left\{{(x-y)}^k/{\left|x-y\right|}^2\right\}}\right)$ (23)

For $a\ne b$  this integral is essentially the linking number

$\varphi \left(C_a,C_b\right)=\frac{1}{4\pi }{\displaystyle \underset{C_a}{\int }d{x}^i{\displaystyle \underset{C_b}{\int }d{y}^j}}{\epsilon }_{ijk}\left\{{(x-y)}^k/{\left|x-y\right|}^2\right\}$ (24)

As long as $C_a$ and $C_b$ do not intersect $\varphi \left(C_a,C_b\right)$ is a well defined integer . Thus ignoring the term $a=b$ , we have $〈W〉=\exp \left(\left(2\pi i/k\right){\displaystyle \sum _{a,b}{n}_a{n}_b\varphi \left(C_a,C_b\right)}\right)$  (25)

The appearance of linking number from the Chern-Simons term associated with the gauge current representing the spin suggest that the linking number can be associated with a spin system. From this analysis it appears that when a DNA supercoil is represented as a spin system the linking number can be considered as a topological invariant related to the Chern-Simon topology associated with the spin system. It should be mentioned that though the linking number is a topological invariant when it is split into twist $\left(Tw\right)$  and writhe $\left(Wr\right)$  these entities are not topological invariants. Since the linking number of a close DNA molecule remains constant during any deformation of the molecule that preserves chemical bonding, it can only be changed by mechanisms in which chemical bonds are disrupted.¹⁵

Elastic properties of DNA molecules

Here we study the elastic properties of a DNA molecule from on analysis of the spin degrees of freedom. As spins are considered here as gauge currents constructed from $SU\left(2\right)$  gauge fields we map the elastic properties onto the space of gauge potentials. To this end we associate the unit tangent vector $\overrightarrow{t}={\partial }_s\overrightarrow{r}\left(s\right)$ where $\overrightarrow{r}\left(s\right)$ depicits a space curve parameterized by arc langth $s$ with the vactor of gauge potentials ${\overrightarrow{A}}_{\mu }$ where the components correspond to the $SU\left(2\right)$  gauge fields $A_{\mu }^a(a=1,2,3)$ $a$  being the gronp index and $\mu$  is the space time index . Evidently ${\partial }_s^2\overrightarrow{r}$  correspond to the $SU\left(2\right)$  gauge field strength ${\overrightarrow{F}}_{\mu \nu }$ . In view of this the internal energy correspondsing to the curvature (bending) given by ${\displaystyle \underset{}{\overset{}{\int }}ds(}{\partial }_s^2\overrightarrow{r}{)}^2$ can be written as ${\displaystyle \int d^{3}x}Tr{F}_{\mu \nu }{F}_{\mu \nu }$ . The twisting elastic energy can be associated with the spin-spin interaction and can be written in the continuum limit as $m^2{\displaystyle \int {\overrightarrow{J}}_{\mu }{\overrightarrow{J}}_{\lambda }{d}^{3}x}$  where ${\overrightarrow{J}}_{\mu }$  is the gauge current¹¹ and ${\overrightarrow{J}}_{\mu }$  is a constant having the dimension of mass. It should be mentioned that this term corresponding to the spin-spin interaction in the continuum limit effectively represents torsion.¹⁸

The elastic energy of B-DNA of length L is given by.⁶

$E_{cl}/k_{B}T=\frac{1}{2}{\displaystyle \underset{0}{\overset{L}{\int }}ds\left[A{({\partial }_s^2\overrightarrow{r})}^2+C{\Omega }^2\right]}$ (26)

 where the deviation in the twisting rate from ${\omega }_0$  is described by the scalar field $\Omega (s)$ ,$A(C)$ being the bending (twisting) elastic constant. When we map this on the configuration space of gauge potentials associated with the spin system, we can write for the elastic energy in the continuum limit.

$E_{cl}/k_{B}T=\frac{1}{2}{\displaystyle \int d^{3}x}[ATr{F}_{\mu \nu }{F}_{\mu \nu }+C{m}^2{\overrightarrow{J}}_{\mu }{\overrightarrow{J}}_{\mu }]$ (27)

where ${\overrightarrow{J}}_{\mu }$ is given by eqn.(11). A significant result of this analysis is that curvature (bending) and torsion (twisting) associated with the deviation from ${\omega }_0$  are not separate entities. Indeed one is related to the other. This follows from the fact that the gauge field curvature $F_{\mu \nu }$ is incorporated in the construction of the current ${\overrightarrow{J}}_{\mu }$ in eqn. (11) which generates torsion. Indeed this interesting relationship between bending and torsion has been pointed out by Nelson¹⁹ suggesting that intrinsic bending can have a huge effect in the transport of torsional stress along DNA.

It may be mentioned that twisting is measured by the spatial rotation rate of base pairs about the central axis which for an undistorted DNA is just ${\omega }_0$ . However for a distorted DNA twisting elastic energy is non-zero when the double-helix twist is altered from ${\omega }_0$ .In this case we have chiral symmetry breaking which is manifested through torsion. It is noted that in the present formalism torsion is generated by the topological current $J_{\mu }^a(a=1,2,3)$  which is related to the axial vector current $J_{\mu }^5=\overline{\psi }{\gamma }_{\mu }{\gamma }_5\psi$  associated with a chiral spinor .In fact each component of the vector ${\overrightarrow{J}}_{\mu }$  in eqn. (11) is related to the axial vector current through the relation²⁰

${\partial }_{\mu }{J}_{\mu }^2=-1/2{\partial }_{\mu }{J}_{\mu }^5$, $J_{\mu }^1=-1/2J_{\mu }^2$, $J_{\mu }^3=1/2J_{\mu }^2$, (28)

In quantum field theory the divergence of this current is non-zero which gives rise to chiral anomaly caused by chiral symmetry breaking .In view of this we find that twisting elastic energy represented by torsion has a correspondence with the chiral anomaly in quantum field theory.

Enyanglement Entropy and DNA molecules

An interwound plectonemic supercoil consists of two helices of the same handedness and at the end of the cylindrical structure the two helices are connected. A solenoidal supercoil is closed by slow distortion of the coil into a toroidal structure. Thermal fluctuation swells up the supercoil radius to larger than the supercoil hard core radius. In fact it has been shown that a repulsive effective entrorpic potential arises opposing the elastically driven collapse at zero temperature.⁶ It impiles that thermodynamic entropy plays a significant role in a DNA supercoil. When DNA molecules are treated as spin systems, it can be shown that supercoils attain the entanglement entropy due to the entanglement of spins. In fact in a supercoil we can consider that the spins associated with each DNA loop are arranged along the axis of the supercoil. As we have pointed out that in a DNA molecule spins are considered to be arranged in an antiferromagnetic chain, the supercoil axis may be treated as a lattice of antiferromagnetic spin system. To have the minimal energy two adjacent spins of opposite orientations will form a singlet. Due to chirality caused by twisting strain into the loop related to torsion the spin system will be in a frustrated state as frustration leads to chirality. This frustration suggests that spin singlets are formed by resonating valence bond (RVB).²¹

It has been shown in some earlier papers^22,23 that the measure of the entanglement of formation given by concurrence $C$  for the entanglement of a pair of nearest neighbor spins is related to the Berry phase24 given by $e^{i{\varphi }_B}=e^{i2\pi {\tilde{\varphi }}_B}$  which is acquired by a spin state when the spins in the system are rotated about the quantization axis (z-axis) in a closed circuit. In fact we have the relation

$C=\left|{\tilde{\varphi }}_B\right|=\left|{\varphi }_B\right|/2\pi$ (29)

It has been observed that the concurrenceassociated with the entanglement of formation for a pair of nearest neighbour spins in a frustrated system is given by $C=0.5$.²² Thus the total concurrence accumulated in the spin chain is given by

$C={\displaystyle \sum _{i=1}^{\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left|{\tilde{\varphi }}_B^{}\right|=\left|{\tilde{\varphi }}_B^{}\right|\left(L/2\right)=\left(1/2\right)\left(L/2\right)=L/4}$ (30)

where L is the total number of spins in the chain and $\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ is the number of singlets. It is noted that the von Neumann entropy for an entangled spin system in a pure state is reduced to the entanglement of formation given by concurrence in a mixed state.25 Thus the above expression (30) represents the entanglement entropy of the spin system. Now we consider that the supercoiled stiff polymer (DNA) is confined inside a narrow tube of radius $r$ . The area of a DNA loop in a supercoil is determined by the number of coils in the loop and hence by the number of spins in the loop. When the supercoiled stiff polymer is confined in a narrow tube of radius $r$  we can associate the area of the surface of the tube with the number of spins in the DNA loop at that serface. Now from the holographic principle which states that for a closed surface entropy is given by the area of the surface the entanglement entropy is found to be given by the area of the surface of the tube. Thus the entanglement entropy can be written in the form

$S_{}\approx r^2/4r_0^2$ (31)

$r$  being the radius of the tube and $r_0$ a fundamental area unit. If we identify $r\approx 2A$  where $A$ is the bending elastic constant and $2A$ corresponds to the step length of an equivalent flexible polymer and $r_0$  is taken to represent the radial displacement of a given point on the coil which is of the order of $R$⁶ we find the entanglement entropy is given by

$S_{}\approx A^2/R^2$ (32)

Similarly for the displacement of a given ponnt on the coil along the superciol axis which is of the order of $\pi P$

 $S_{}\approx A^2/{\left(\pi P\right)}^2$  (33)

So the total entropy is given by

$S_{}=A^2/R^2+A^2/{\left(\pi P\right)}^2$ (34)

 Now we observe that this entanglement entropy effectively corresponds to the thermodynamic entropy. Indeed for a tube of narrow radius entanglement entropy cannot vanish whereas in the limiting case of radius $r\to 0$  we can think of zero radius (straight line) when the total elastic energy vanishes at zero temperature. In this case the entanglement entropy also vanishes. In fact at zero temperature an elastic tube will collapse into a plectonemic supercoil when subject to the constraint $\Delta Lk/L\ne 0$ [26]. When $\Delta Lk$  is put into writhe $(Wr)$  the twist energy becomes zero. Then we can make the plectoneme collapsed into a line ($\mathrm{Sin}\gamma =1$ ) which makes the bending energy zero also. Now at zero temperature the area of the loop vanishes. In this case the entanglement entropy also vanishes. In view of this we can identify the entanglement entropy as the thermodynamic entropyof the supercoil.

 This helps us to compute the free energy associated with the supercoil. We note that from the relation $dF=SdT$ , $F(T)$ being the free energy (temperature) , we note that the free energy per unit volume associated with the entropy given by eqn.(34) can be written as

$\Delta F/\left(K_{B}TV\right)\approx A^2/\left(R^2{r}^3\right)+A^2/\left\{{\left(\pi P\right)}^2{r}^3\right\}$ (35)

This gives the free energy per unit length

$\Delta F/\left(K_{B}TL\right)\approx A^{2/3}/\left(R^{2/3}r\right)+A^{2/3}/\left\{{\left(\pi P\right)}^{2/3}r\right\}$  (36)

Now as argued above $r$ is taken to be of the order of $A$  and hence we find

$\Delta F/\left(K_{B}TL\right)\approx A^{2/3}/\left(R^{2/3}A\right)+A^{2/3}/\left\{{\left(\pi P\right)}^{2/3}A\right\}$

=$1/\left(A^{1/3}{R}^{2/3}\right)+1/\left(A^{1/3}{\left(\pi P\right)}^{2/3}\right)$  (37)

This result is identical with that obtained by Marko and Sigga⁶

A crucial implication of our result is that as entanglement of a quantum system is the major resource in processing quantum information,^27,28 the entanglement entropy determines the quantity of information which can be used for transcription. When DNA is regarded as linear repository of sequence information we note that this entanglement entropy determines the quantity of genetic information in a supercoil which can be transcribed.

DNA molecule as a skyrmion energy

A DNA molecule is characterized by certain topological feature such as linking number. At length scale of thousands of base pairs DNA is organized into topologically independent loops. There are situations in vivo when topological constraints lead to supercoiling. DNA loops in a supercoil may behave as a topological object such as a soliton (skyrmion) which is realized when we consider DNA as a spin system. In fact DNA loops in a supercoil when constrained by a change in the linking number due to deviation of twisting rate from ${\omega }_0$  correspond to the formation of a spin texture when a DNA molecule is considered as a spin system. A change in the linking number from $L{k}_o$ due to twist of the ends causing a deviation from the planar circle configuration corresponds to a spin texture and represents a deviation of the spin system from the ground state when spin excitations occur. These excitations resemble the solitons (skyrmions) described by the nonlinear $\sigma$ -model.

As mentioned in sec.2 a spin may be depicted in terms of fermionic oscillators. We can depict a two-component spinor as $\left[\begin{array}{c}u\\ v\end{array}\right]$ with

$u=\cos \raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.e\raisebox{1ex}{$i\varphi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ (38a)

$v=\sin \raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.e\raisebox{1ex}{$-i\varphi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ (38b)

In terms of the spin system we can consider the ground state wave function depicting the DNA supercoil with linking number $L{k}_o$

$\left|{\psi }_0\right.〉={\displaystyle \prod _{i\langle j}\left(u_i{v}_j-v_i{u}_j\right)}$ (39)

where $i$ and $j$ correspond to the spin sites. When the linking number deviates from $L{k}_o$ due to deviation of the twisting rate from ${\omega }_0$ , the resulting skyrmion state is described by

$\left|\psi \right.〉=C{\displaystyle \prod _k\left(\begin{array}{c}{v}_k\\ -\alpha u_k\end{array}\right)\left|{\psi }_0\right.〉}$ (40)

where the spin texture is included within the components $v_k$  and $u_k$  and $0\le \alpha \le 1$ .²⁹ If a smooth and monotonical function $g\left(\theta \right)$  is defined with $g\left(0\right)=0$ and $g\left(\pi \right)=\pi$  then the skyrmion state can be written as

$\overrightarrow{\varphi }(\Omega )=\cos (g(\theta )-\theta ){\overrightarrow{e}}_r+\sin (g(\theta )-\theta ){\overrightarrow{e}}_{\theta }$ (41)

where ${\overrightarrow{e}}_r$  and ${\overrightarrow{e}}_{\theta }$  are the basis vectors. The size of a skyrmion is determined by the function $g\left(\theta \right)$  and $g\left(\theta \right)=\theta$  describes the hedgehog skyrmion with spin in the radial direction $\overrightarrow{r}$ .

The skyrmion state $\overrightarrow{\varphi }(\Omega )$  is constrained by the relation $\left|\overrightarrow{\varphi }(\Omega )\right|=1$ . The quantum state for the skyrmion $\overrightarrow{\varphi }(\Omega )$ can be written as

$\left|\psi \right.〉=C{\displaystyle \prod _k\left(\begin{array}{c}\sin \raisebox{1ex}{$g({\theta }_k)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.e\raisebox{1ex}{$-i{\varphi }_k$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\\ -\cos \raisebox{1ex}{$g({\theta }_k)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.e\raisebox{1ex}{$i{\varphi }_k$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\end{array}\right)\left|{\psi }_0\right.〉}$ (42)

where $C$  is the normalization constant and $g\left(\theta \right)$  controls the size of the skyrmion. From equ. (41) and (42) it is seen that $0\le \alpha \le 1$  is determined from $g\left(\theta \right)$ and $\alpha$ controls the size of the skyrmion . Indeed we can define

$\theta =2\arctan \alpha$    (43)

which equals $\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ for the hedgehog skyrmion with $\alpha =1.$

Taking the spin variable $\overrightarrow{z}=U{\overrightarrow{z}}_0$ with ${\overrightarrow{z}}_o=\left(\begin{array}{c}1\\ 0\end{array}\right)$ and $U\epsilon SU\left(2\right)$ we may write the nonlinear $\sigma$ -model Lagrangian in terms of the $SU\left(2\right)$  matrices $U$  as [30]

$L=-\left(M^2/16\right)\left({\partial }_u{U}^{\text{†}}{\partial }_{\mu }U\right)-\left(1/32{\eta }^2\right){\left({\partial }_{\mu }U{U}^{\text{†}},{\partial }_{\nu }U{U}^{\text{†}}\right)}^2$  (44)

where $M$ is a constant having dimension of mass and $\eta$ is a dimensionless parameter, $\mu ,\nu$ being space -time indices. The $\alpha$  dependence may be incorporated through $M$ and $\eta$ where these parameters are taken as functions of $\alpha$ . For a distorted loop we can consider the radius of the loop $R$  as a function,$R(\theta ,\varphi )$ corresponding to the core radius of the skyrmion. We can define the core size of the skyrmion such that $R=R_0\left(1-\alpha \right)$  where $R_0$  is the size of the skyrmion with minimal energy. The static nonlinear $\sigma$  -model Lagrangian corresponding to eqn. (44) gives rise to the energy integral as

$E={\displaystyle \int d^{3}x\left\{\left(M^2/16\right)Tr\left(\nabla U^{\text{†}}\nabla U\right)+\left(1/32{\eta }^2\right)Tr{\left[{\partial }_{i}U{U}^{\text{†}},{\partial }_{j}U{U}^{\text{†}}\right]}^2\right\}}$ (45)

where $i,j=1,2,3$  are spacial indices. To compute the energy we take the Skyrme ansatz

$U(x)=\exp (iF(r)\overrightarrow{\tau }.\widehat{x}$ (46)

where $\overrightarrow{\tau }$ are Pauli matrices, $\stackrel{\wedge }{x}=\frac{\overrightarrow{x}}{r}$  and $F(0)=\pi$  and $F(r)\to 0$  as $r\to \infty$ . We explicitly write

$U=\cos F(r)+i\overrightarrow{\tau }.\widehat{x}\sin F(r)$        (47)

with

$\cos F(r)={\left(1-\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)}^2/{\left(1+\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)}^2$  and

$\sin F(r)=2\left(\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)/1+{\left(\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)}^2$ (48)

The energy integral becomes

$E(R)=4{\pi }^2{M}^{2}R{I}_1+2{\pi }^2\left(I_2/{\eta }^{2}R\right)$  (49)

where

$I_1=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\alpha }{\int }}dx}\left[{\sin }^{2}F(r)+x^2{\left(\partial F/\partial x\right)}^2\right]=3.0$  (50)

and

$I_2=\left(1/\pi \right){\displaystyle \underset{0}{\overset{\alpha }{\int }}dx}\left[\left({\sin }^{4}F(r)/x^2\right)+{\sin }^{2}F(r){\left(\partial F/\partial x\right)}^2\right]=1.5$  (51)

with $x=\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$R$}\right.$ . This gives the expression of energy

$E(R)=12{\pi }^2{M}^{2}R+\left(3{\pi }^2/{\eta }^2{R}^{}\right)$        (52)

The minimum of energy $E(R)$ is found from the relation

$\partial E(R)/\partial R=12{\pi }^2{M}^2-3{\pi }^2/{\eta }^2{R}^2=0$ (53)

which gives for $E_{\min }$  the size as

$R_0=1/2M\eta$            (54)

and the energy

$E_{\min }=E(R_0)=12{\pi }^{2}M/\eta$  (55)

It is noted that the coupling parameters $M$  and $\eta$  are functions of $\alpha$  such that in the limit $\alpha \to 0,M(\alpha )\to 0$  and $\eta (\alpha )\to 0$ but $\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$\eta $}\right.$  is fixed. When we take $R=R_0\left(1-\alpha \right)$ we have          $E(R)=\left\{\left(6{\pi }^{2}M\right)/\eta \right\}\left[\left(1-\alpha \right)+1/\left(1-\alpha \right)\right]$  (56)

Now we note that the parameter $\alpha$ effectively gives a measure of the chirality associated with twisting strain into the loop given by $\sigma =\left(\Delta Lk/L{k}_0\right)$ .In fact in the simplest form we can take $\alpha =k\left|\sigma \right|$ where $k$  is a constant. So form the relation $R=R_0(1-\alpha )=R_0(1-k\left|\sigma \right|)$ , we can estimate the energy of a DNA loop as a function of $\sigma$ . It is noted that the relation $R=R_0(1-\alpha )$  gives a nonzero size for $\left|\sigma \right|<0.02$  when $R_0$  is infinite. Indeed it has been found that for $\left|\sigma \right|<0.02$  the minimal free energy state has $R=P=\infty$  indicating that no consistent stable supercoiled state exists for small $\left|\sigma \right|$ . For $\left|\sigma \right|>0.02$  the plectonemic free energy exhibits a minimum value for finite $R$ and $P$ which implies that we have a stable supercoiled state. It appears that $\sigma$  can be varied through roughly -0.1 to 0.1 as beyond these bounds the double helix is unstable.31 These observations are found to be consistent with this skyrmion model.

In Figure 1 we have plotted the radius $R$  of a plectonemic supercoil as a function of $\alpha$  where $R$ is given by $R=R_0(1-\alpha )$  with $\alpha =k\left|\sigma \right|$ . The constant k is determined from the experimental data7 and the best fit is given by k=8.333.

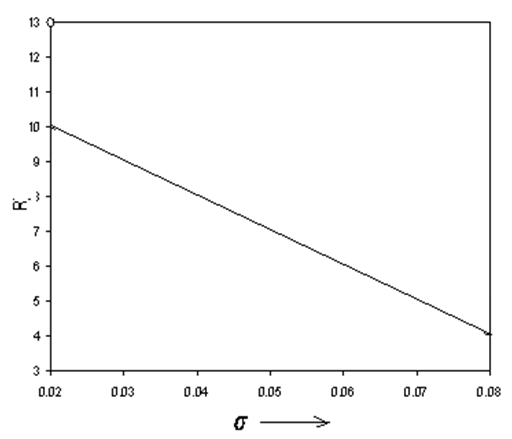
Figure 1 Radius  of a plectonemic supercoil as a function of  where. The constant k is determined from the experimental data⁷ and the best fit is given by k=8.333.

From our analysis it appears that when the long linear chromosomal DNA molecules are organized into loops, these topological independent loops appear as solitons. Solitons are nonlinear excitations which can travel as coherent solitary waves. The present analysis implies that soliton excitations may well exist in DNA chains which is consistent with the observations of Englander et.al.³² The linking number associated with a supercoil is given by the topological charge of the loops. As the skyrmion (soliton) depicting a loop is described by the nonlinear $\sigma$ - model in terms of $SU\left(2\right)$  gauge fields, the topological charge of a loop is given by the winding number of the mapping of the 3-space manifold into the group manifold $SU\left(2\right)=S^3$  which corresponds to homotopy ${\pi }_3(SU\left(2\right))={\pi }_3(S^3)=Z$  where $Z$  represents the set of integers. When DNA loops supercoil the linking number is given by an integer determined by this homotopy group so that $Lk=nZ$  where $n$  is the number of superhelix loops.

Effect of noise on DNA spin chain

We find the effect of noise in the Berry phase of quantized spinor and in its entangled state both in the presence and the absence of spin –echo method, on the influence of classical fluctuation of field on Berry phase of spin ½ particle.^33–35 We define noise by a shift like residual dipolar couplings crucially (RDCs). If we consider that with the lapse of time, the parameter $\lambda$ suffer a deviation $\lambda \to \lambda +\delta \lambda$  due to any change in $\theta$  , $\varphi$ ,$\xi$  resulting a gauge transformation .

$Z(\lambda )\to Z(\lambda )+\frac{\partial Z(\lambda )}{\partial \lambda }\delta \lambda$ (57)

Here $Z(\lambda )$  is the gauge connection associated with the Lagrangian in this eqn.10.b , this equation giving rise to Berry phase.

This fluctuation of gauge relations by the parameter $\lambda$ , is the extremely cause of transfer in magnetic flux line equivalent chiral equilibrium contravention. Now the necessary geometrical phase of the only quantized spinor eqn. 10.c, This shows that for quantized spinorthe Berry Phase is a solid angle subtended about the quantization axis. For $\theta =0$ the minimum value of ${\Delta }^{up}$ is 0 and $\theta =\pi$ maximum.

Spin up case we have

$Z^{up}(\lambda )=(1/2)(1-\cos \theta )$  (58)

This leads to have the noise dependent Berry Connection of the quantized spinor

$Z^{up}(\lambda )=(1/2)(1-\cos \theta +\sin \theta \delta \theta )$  (59)

Now the result a modification of Berry phase

${\Lambda }^{up}=\pi (1-\cos \theta +\sin \theta \delta \theta )$  (60)

And similar for down spinor

${\Lambda }^{down}=\pi (1-\cos \theta -\sin \theta \delta \theta )$ (61)

Where we consider ${\Lambda }^{up}$ ,${\Lambda }^{down}$ as the noise induced Berry phase for the spin up and spin down quantized practices in that order [36-38]. Now the entangled state of two identical spinor, as we find in eqn.3.c, that the evolution of the state at a exacting instant depends on the distinction of ${\Delta }^{up}$ and${\Delta }^{down}$ which implies boost of noise by twice. The effect of noise in the entangled state formed after ’spin-echo’ will be less as realized from eqn. 3.e. On the conclusion, we similar to observation that here the noise is accountable for the fluctuation of quantization that can be practical for the entanglement of Quantum Hall particles in the non-plateau and plateau area.

We have shown that a DNA supercoil can be treated as a quantum spin system such that spins are located on the axis forming an antiferromagnetic chain .These spins can be associated with $SU\left(2\right)$ gauge field currents when gauge fields lie on the links. We have formulated bending (curvature) and twisting (torsion) in terms of these gauge fields. A significant result of this formalism is that bending and twisting are not independent entities. In fact bending influences the propagation of twisting strain along the DNA which has been supported by experiments. The formulation of DNA supercoil in terms of an antiferromagnetic spin chain gives rise to the entanglement entropy which induces the entropic protential associated with the free energy per length corresponding to the entropy cost of confining a stiff polymer inside a narrow tube. The entanglement entropy effectively represents the thermodynamic entropy and this repulsive entropic potential opposes the elastically driven collapse of a supercoil which can occur at zero temperature. The entanglement entropy has a very significant implication in that it measures the total information content in the system. Indeed when a DNA is regarded as a linear repository of sequence information the entanglement can be used to transcribe information and entropy determines the quantity of information which is available for transcription. In view of this a measure of this entanglement entropy can be taken to determine the quantity of genetic information which can be transcribed. This helps us to consider genetic information transcription as a manifestation of quantum information theory.

Another interesting aspect of our analysis is that a DNA loop can be treated as topological object depicted as a skyrmion (soliton) which arises due to the excitation of spins caused by the deviation of the twisting rate from ${\omega }_0$ leading to excess (deficit) of linking number. The spin texture is determined by the twist parameterized by the quantity $\sigma =\left(\Delta Lk/L{k}_0\right)$ . The energy of the skyromion depicting a DNA loop depends on the radius which is determined by the parameter $\sigma$ . The linking number of a DNA molecule when organized into loops is related to the topological charge of a skyrmion depicting a loop. Also the dynamical phase of DNA molecule can be separate in the spin-echo system. During this process the addition of Berry phase in the entangled state is accountable for the calculate of entanglement. Variation in DNA molecule helicity is considered as noise that change the fixed significance of Berry phase.³⁹ The consequence of noise doubles as two pure identical spinor entangle. We like to study further this effect of noise, decoherence and entanglement in association with quantization feature of Berry phase in previous quantum aspect DNA molecule development.

The authors are grateful to express my deep gratitude to my beloved Sir Prof. Pratul Bandyopadhyay for helpful discussion.

1. A Worcel, E Burgi. On the structure of the folded chromosome of Escherichia coli. J Mol Biol. 1972;71(2):127–147.
2. C Benyajati, A Worcel. Isolation, characterization, and structure of the folded interphase genome of Drosophila melanogaster. Cell. 1976;9(3)393–407.
3. DA Jackson, P Dickinson, PR Cook. The size of chromatin loops in HeLa cells. EMBO J. 1990;9(2):567–571.
4. LA Freeman, WT Garrard. Critical Reviews™ in Eukaryotic Gene Expression. Crit Rev Euk Gene Exp. 1992;2(1):165.
5. JF Marko, FD Siggia. Bending and twisting elasticity of DNA. Phys Rev E. 1990;52(1):2912.
6. TC Boles, JH White, NR Cozzarelli. Structure of plectonemically supercoiled DNA. J Mol Biol. 1990;213(4):931–951.
7. J Bednar, P Furrer, A Stasrak, et al. The Twist, Writhe and Overall Shape of Supercoiled DNA Change During Counterion-induced Transition from a Loosely to a Tightly Interwound Superhelix: Possible Implications for DNA Structure in Vivo. J Mol Biol. 1994;235(1994):825–847.
8. G Goswami, P Bandyopadhyay. Spin system, gauge theory, and renormalization group equation. J Math Phys. 1995;34(2)749.
9. P Bandyopadhyay. The geometric phase and the spin-statistics relation. Proc Roy Soc (Londan)A. 2010;466(2122):2917.
10. AI Abanov, PB Wiegmann. Theta-terms in nonlinear sigma-models. Nucl Phys B. 2000;570(2):685.
11. M Carmeli, S Malin. The gauge-theoretical structure of general relativity and the new conserved current. Ann Phys. 1977;103(1):208–210.
12. I Calugareau, Crechoslovak. Sur les classes d’isotopie des noeuds tridimensionnels et leurs invariants. C Math J. 1961;11(1):588.
13. JH White. Self-Linking and the Gauss Integral in Higher Dimensions. Am J Math. 1969;91(3):693–728.
14. D Swigon. The Mathematics of DNA Structure, Function and Interactions. In: CJ Benham et al. editors. Springer Science Business Media). 2009. p. 1–28.
15. FB Fuller.  Decomposition of the linking number of a closed ribbon: A problem from molecular biology. Proc Natl Acad Sci (USA). 1979;75(8):3557–3561.
16. AM Polyakov.  Fermi-bose transmutations induced by gauge fields. Mod Phys Lett A. 1988;3(3):325–328.
17. A Bandyopadhyay, P Chatterjee, P Bandyopadhyay. Quantum Gravity Effect in Torsion Driven Inflation and CP violation. Gen Rel Grav. 1986;18:1293.
18. P Nelson. Transport of torsional stress in DNA. Proc Natl Acad Sci (USA). 1999;96(25):14342–14347.
19. A Roy, P Bandyopadhyay. Topological aspects of a fermion and the chiral anomaly. J Math Phys. 1989;30(10):2366.
20. PW Anderson. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science. 1987;235(4793):1196–1198.
21. B Basu, P Bandyopadhyay. Spin Entanglement of Two delocalised Fermions and Berry Phase. Int J Geo Meth Mod Phys. 2007;9(2):707–710.
22. B Basu,d P Bandyopadhyay. Spin entanglement of two delocalized Fermions and Berry phase. J Phys A. 2008;41(2008):055301.
23.  MV Berry. Quantal phase factors accompanying adiabatic changes. Proc Roy Soc (Londan) A. 1984;392(1802):45.
24. TJ Osborne, MA Nielson. Entanglement in a simple quantum phase transition. Phys Rev A. 2002;66:032110.
25. NG Hunt, JF Hearst. Elastic model of DNA supercoiling in the infinite‐length limit. J Chem Phys. 1991;95(12):9329.
26. CH Bennett, DP Divincenzo. Quantum information and computation. Nature. 2000;404:247–255.
27. MA Nelson, GL Chuang. Quantum Information and Quantum Compoutation. (Cambridge University Press, Cambridge). 2000.
28. B Basu, S Dhar, P Bandyopadhyay. Quantum hall skyrmions in the framework of O(4) nonlinear sigma model. Int J Mod Phys B. 2004;18(2):171–184.
29. THR Skyrme. A unified field theory of mesons and baryons. Proc Roy Soc A. 1962;31:556–569.
30. NR Cozzarelli, TC Boles amd, J White. In DNA Topology and its Biological Effects. In: NR Cozzarelli et al., editors. Cold Spring Harbor Laboratory, Cold Spring Harbor,  New York). 1990.
31. SW Englander, NR Kallenbach, AJ Heeger, et al. Nature of the open state in long polynucleotide double helices: possibility of soliton excitations. Proc Natl Acad Sci (USA). 1980;77(12):7222–7226.
32. G De Chiara, G Massino Palma. Berry Phase for a Spin 1/2 Particle in a Classical Fluctuating Field. Phys Rev Lett. 2003;91:090404.
33. P Bandyopadhyay. Conformal field theory, quantum group and Berry phase. Int Jor of Mod Phys A. 2000;15:1415–2000.
34. GP Berman, GD Doolen, R Mainnier, et al. Introduction to Quantum Computers. World Scientific. 1998. p. 1–197.
35. S Singha Roy. DNA Molecule as a Spin System and the Symmetric Top Model. Theoretical Physics. 2017;2(3):141–144.
36. S Singha Roy, P Bandyopadhyay. Quantum perspective on the localized strand separation and cyclization of DNA double helix. Phys Lett A. 2018;382(30):1973–1977.
37. SS Roy, P Bandyopadhyay. DNA Molecule as a Spin System and the Symmetric Top Model. Phys Lett A. 2013;337:2884.
38. B Basu, P Bandyopadhyay, P Majumdar. Magnetic field dependence of the entanglement entropy of one dimensional spin systems in quantum phase transition induced by a quench. Phys Rev A. 2012;86:022303.
39. SS Roy, P Bondyopadhyay. Entropy-driven denaturation and bubble nucleation in DNA melting. Euro Phys Lett. 2015;109(4):48002.