Our observations of magneton with Ferrolens shows evidence pointing to such magneton entity, and more evidently in recent results with the synthetic vacuum unipole experiments. Physics formalism ansatz novel model analyses demonstrate how vacuum quanta may have sufficient energy for vacuum genesis, by constructing eigen spinors of zero_point microblackhole Hamiltonian quantum mechanics with Helmholtz decomposition matrix of gradient and rotational tensors, that are characteristic of translational vortex fields. With these mathematical physics processes, we obtain resulting energy fields spatial property partial differential equations characterizing eigen state energetics of zero point vacuum quagmire, as well as eigen state vortex fields of micro black hole, both together making up plasmodial zones within quagmire. Specific eigen spinors Hamiltonian partial differential equations quantifying energy and fields eigen functions. Vacuum that is dipole vacuum may have superposition of complex input of quagmire vortex fields acting to create non–hermitian quantum relativistic physics.

Keywords: quantum cosmology, vacuum space quanta, Hamiltonian operator, eigen functions, magneton, observables, general formalism, Hamiltonian analysis, vortex vacuum eigen spinors, gradient zero point source rotational micro black hole sink tensors

Energetics of a vacuum space quanta that maybe unit of fabric of vacuum space had been quite perplexing physicists over many centuries, from classical to relativistic to quantum mechanics.^1,2 Classical physics with Galilean Newtonian equations of motion and Maxwell’s electro vacuum equations^3–5 started to analyze quantitatively nature of gravity, space, and time, although it was elusive to explain wholesomely universal phenomena from micro to macro universe.^6,7 Einstein’s relativistic theories proposed a way of bringing together the concept of space and time, topologically, to explain gravity to unify all four forces of nature known to humans: electromagnetism, strong and the weak nuclear forces, and the gravity.^8–11 Fundamentally, pure, and applied mathematics had been all the while playing a major role in quantifying physics through enabling parametric measurements of observations.¹² To explain the microcosm of universe, quantum mechanics with Schrodinger’s wave function Hamiltonian equations came to explain the duality of the wave and particle aspects, with de Broglie’s assertion of simultaneity of energy and matter presence.¹³ Standard Model had put together spectra of quantum particles, with Higgs Boson identifying observable as the mass giver for particles, that will evolve onto real matter into existence.¹⁴ Quantum density matrix had formed the flavor of special unitary symmetries constituting typical gage invariance,¹⁵ with many grand unified theories establishing necessity of monopoles existing to account for energy densities of universal systems. However, the question of origin of energy and of quantum vacuum had been eluding physicists’ total quantify ability. Parametric analysis with experimental observations had posed a measurement problem. In his original introduction of mathematically provable quantization of monopole –charge aspects, noting knowhow physics, Dirac argued quantitatively vacuum quantum necessitating existence of monopoles based on fundamentals of quantum mechanics.¹⁶ To understand about vacuum space quantum vortex systems, generalized and/or modified Maxwell equations to include monopoles had been advanced mathematically analytically.¹⁷ A detailed knowledge with mechanics of quantifying vortex systems to monopoles¹⁸ to more specific Lagrangian and Hamiltonian derivation mathematically of vortex systems suitable to analyze vacuum quagmire with monopole & the dipole had already been modeled.^2,19–23 These studies show that monopoles’ physics had mechanics like the fluid system’s hydro dynamical vortex systems Searches for monopoles, with scientists all over the world, consisted of two categories experimentally typically: (1) detecting preexisting monopoles, (2) creating and detecting then new monopoles.^24–33 Mathematical techniques explored here to solve eigen value problem might set a precedence to abstract who listic observational physics with mathematical preciseness, applicable further to provable generalized quantum relativistic grand formalism. In this paper, Helmholtz decomposition fields are only considered to come up with general formalism, especially since research experimentation measurements with Ferrolens observational results have shown that magnetism is exclusively a dipole phenomenon, which in contrast to eclecticism, hence cannot be mono pole. If an isolated natural occurring magnetic monopole charge is found, it would not create a gauge field – force field spatially around it radiated in space, all energy flows inward with none radiated outside, whereas a monopole electric charge which is a physically spinning magnetic dipole charge, radiates energy to the outside and therefore can create a field.^34,35

Standard techniques established by vast amount of quantum physics literature on constructing, analyzing, interpreting, quantifying as well as problem solving eigenvalues, eigenmatrices, eigenvectors, and fields of Hermitian and/or non –Hermitian Hamiltonian operator^36–43 generating characteristic energy and field spectrum were widely utilized here to configure quantum characterization of matrix systems. Within all theoretical endeavors, matrix rules and quantifiable formulations follow integrated procedures configured from the research of physics literature articles, samples of which appear in the reference list, with^44–48 in this paper. Zero –point analysis of quantum vacuum would refer to energy at the vacuum quanta zero –point fluctuation energy.^49,68 Micro –black holes considered here in analysis would essentially be quantum blackholes.^51,52 General theoretical modeling is extendable to ansatz modeling superluminal multiphase systems that will grand unify fields, while explaining how such high energies originate in primordial universe.

Explanations of magneton, quantum magnet, and type of fields they exhibit:^{53–56,58,59}

The term magneton⁵³ refers to the elementary magnetic dipole quanta of any magnetic dipole charge either if it is an electron or quark or any particle that has a 1/2 spin, i. e. fermions.⁶⁰ The difference of the Bohr magneton with the term we are using "magneton" is that the Bohr magneton refers to the bound electrons of an atom whereas the term magneton refers in general to the "Quantum Magnet" and magnetic moment of any particle either it is free or bound in the atomic structure.^53–56 In any event, the magneton⁵³ is a monopole charge. With that said, our observations with the ferrolens of the Quantum Magnet field⁵³ reveals that it consists of two opposite magnetic monopole charges thus two joint counter rotating magnetic flux monopole vortices jointed together to form a magnetic dipole or else a magnetic flux dipole vortex.^53–56,61 This is now exactly to what our term "magneton"⁵³ refers to, according to our research.^53–56 However, any vortex field is essentially a monopole field,⁵⁸ therefore our observation and previous research reveals that the nature of the Quantum Magnet is essentially Gilbertian in nature and not Amperian.⁵⁹ Thus, it effectively consists of two joint monopoles of opposite magnetic charges, the only form in our space time magnetic monopole charges can exist, i. e. jointly in a dipole formation.^53–56

Now, one of the central emphases with theory of the paper will be based on the conjecture that in our space –time these dipole magnetons⁵³ can exist only as dipoles but in the super luminous energy phase of vacuum space, per Figure 1, the magnetons⁵³ exist only as monopole energy vortices thus monopole magnetons,⁵³ vibrating at super luminous speed and are like the pixels and elementary quanta of discrete vacuum space occupying each point of it. Consequently, in the fabric of our space time, for whatever reason these monopole magnetons⁵³ lose their super luminous kinetic energy and drop down their energy level to luminous or sub luminous, brought out in Figure 1, they change phase and fall into our space time and instantly join into elementary magnetic dipoles, thereby forming the basis of fermionic matter in our universe. In the super luminous phase of vacuum space, this is totally undetectable by us and perceived by us as "empty space" in our space time.

Figure 1 Schematic showing super luminous phase of vacuum space monopole magnetons^53–56 essentially empty space manifesting subsequent phase transitions.
Schematic sketching of phase transitioned luminous and sub luminous phase of vacuum space Einsteinian space time formation of dipole magnetons.^53–56

Our recent observations of magneton with Ferrolens quoted literature^53,56 briefly show within the Figures 2 & 3 real –time observations of quantum field magnetism (QFM) of vortex dipoles, as well as physical mechanism explaining classical macroscopic electric E –field of a macro vacuum quantum dipole field, having vortex casuality effects, that are observed with the Ferrolens.⁵³ Hedgehog field lines displayed by the Ferrolens, diverging out of the unipolar vacuum ring array’s vortex field shows effect of synthetic monopole quasi particle effect, like a ferro vacuum Dirac quantum vacuum monopole trap, referring to Figure XI (source: Emmanouil Markoulakis et al.)⁵⁶ Also, screw –like unipole vortex formations, and non –classical vortex quantas, that appear as Quantum Magnet Field (QMF) Figure IV & X (source: Emmanouil Markoulakis et al.)⁵⁶ are indicative of special features of monopole –like unipole synthetic vacuum array. Apart from our recent results, highlighted above suggesting monopoles spontaneously transform to dipoles, further observation with the vacuum 3D fields visualizations^53–56 have proved that magnetons⁵³ form the fundamental fields and that they are constituted by uni poles, quite likely building blocks of everything universally.

Figure 2 (a) A logarithmic spiral. (b) QFM vortex dipole field magnetism. (c) left arm of spirutal segment of the QFM. (d) Right arm spiral segment, these measurements comparatively show real-time observations originally per Figure VI (source: Emmanouil Markoulakis et al.)⁵³ measurements with the Ferrolens.⁵³

Figure 3 Physical mechanism for explaining classical macroscopic E-field of macro vacuum quantum field dipole magnetism with vortex casualty effect originally Figure VI (source: Emmanouil Markoulakis et al.)⁵³ observations with the Ferrolens.⁵³

We are attempting to establish theoretical basis to mathematically analyze these systems, with a key goal of identifying observables that are provable verifiably with experimental techniques, such as the quantum vacuum –optic flux viewer Ferrolens to probe inside the ferro vacuum materials, as well as Bose –Einstein condensate that can detect polar –core spin vortices especially of Dirac monopole. Standard techniques established by vast amount of quantum physics literature on constructing, analyzing, interpreting, quantifying as well as problem solving eigenvalues, eigen matrices, eigenvectors, and fields of Hermitian and/or non –Hermitian Hamiltonian operator^36–45 generating characteristic energy and field spectrum are widely utilized to configure characterization of quantum vortex systems considered here. In all theoretical endeavors, matrix rules and quantifiable formulations follow integrated procedures that are adapted from the research of physics literature articles, samples of which appear in the reference list, with^{44–48,62,64,67} in this paper.

Simple reasons that justify formalism, applying Helmholtz decomposition fields analysis of vortex dynamics:

1. Magneton⁵³ experimental observations measurements show that the vortex fields are main characteristics. Helmholtz decomposition fields have already in –built rotational (vortex) fields and the gradient fields,^57,62–69 which provide driving force to vortex fields, metrics, that can be expressed as a 2x2 matrix.
2. It is possible to transform from Helmholtz metrics, using Coulomb gage that will link to Coulomb branch gage groupwith Hilbert series having SuperSymmetry (SUSY) Quantum Field Theory (QFT) charge conjugation.^57,70 We can then link charge conjugation to rotating charges per Dirac Maxwell Einstein Kerr Newmann metrics.^71,72
3. Hence, in this formalism, we adopt Helmholtz decomposition fields tensor matrixapproach, due to above mentioned reasons.

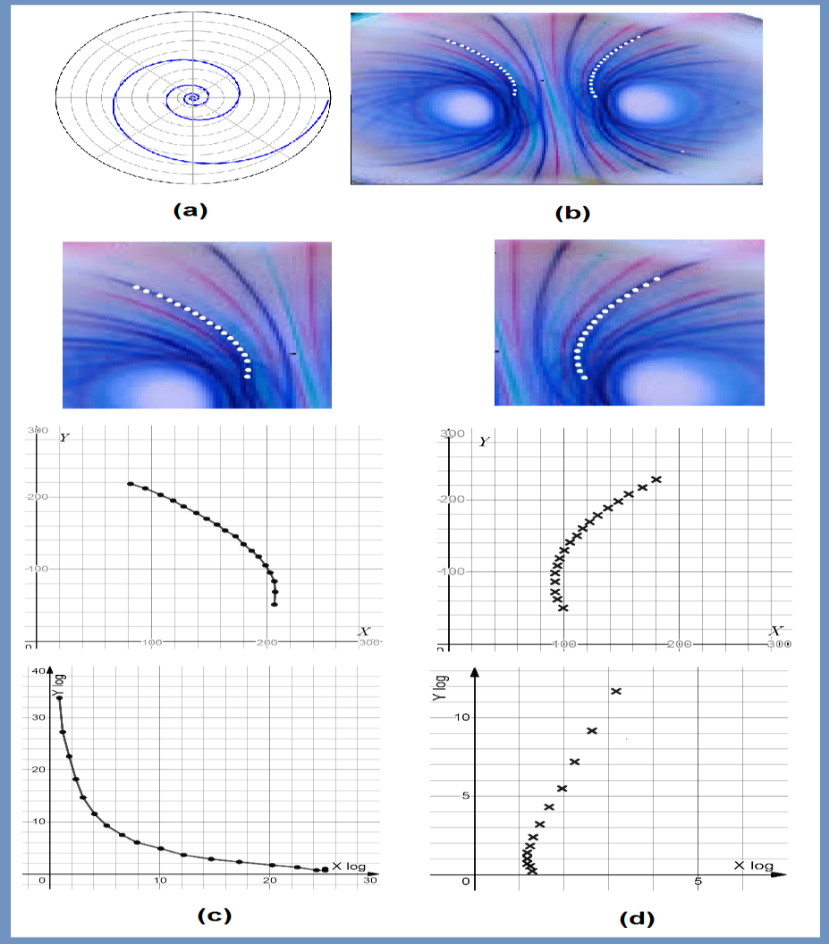
Helmholtz mathematical physics theorem⁶² describes how a vector field can be expressed as a gradient scalar potential and a curl of vector field potential. We will expect the curl of the field being zero at the zero point,⁶³ where authors have argued that for each stationary classical background field there is a ground state of the associated quantized field; this is the vacuum for that background. Helmholtz theorem has generality that can be used to connect quantum with relativitistic physics.⁶⁴ On the other hand, gradient of field zero at a black –hole with a nonzero curl⁶⁵ causes highly energetic compaction within increasing internal pressure asymptotically; here authors have brought out the effect of rotation on simulations of black hole events at the LHC showing that the angular momentum of the black hole cannot be ignored, and it makes a non –trivial contribution for most of the lifetime of the black hole. A key consequence of the rotation of the black hole is that the Hawking radiation is no longer isotropic, making it more difficult to infer space –time parameters from measurements of the emitted particles.⁶⁵ In this letter, they had studied the angular distribution of the Hawking emission of non –zero spin particles with specific helicity on the brane, arguing that the shape of the distribution could be used as a measure of the angular momentum of the black hole.⁶⁵

The Helmholtz theorem vector decomposition of field⁶⁶ equates $F=-\nabla \Phi +\nabla xA$ , where F is a vector field defined on a bounded domain $V\subseteq R3$ , which is twice continuously differentiable, having surface S enclosing domain V. F then thus can be decomposed into a curl –free component and a divergence –free component, such that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational (curl –free) vector field and a solenoidal (divergence –free) vector field. This is known as the Helmholtz decomposition,⁶⁶ with $\Phi =$ scalar potential; $A=$ vector field potential; thereby, $F=-$ grad $\Phi +$ curl.

Upper and the lower indices, such as $\epsilon \mu \nu \&{\epsilon }_{\mu \nu }$ , considered here in our detailed analysis of the general field tensors, follow normal tensor calculus mathematical notations.⁶⁷ The zero –point vector field above brings out interesting situation of curl $A->0$ , which is justifiable since rotational component will not exist at zero –point, although grad $\Phi \ne 0$ ; conversely, at a micro –black –hole, $F->0$ , where the field may be collapsed electro vacuum light – electric + vacuum – vector field, and then $\nabla xA=\nabla \Phi –$ perhaps manifesting as Hawking radiation out of zero –point within a micro –black –hole. This is a conjecture borne out of Poincare’s Theorem stating that if $\nabla xF=0$ (i.e $.,F\left(x\right)$ is an irrotational field) in a simply connected neighborhood U(x) of a point x, then in this neighborhood, F is the gradient of a scalar field $\phi \left(x\right)$ .⁶⁸ Rotational component is associated through Helmholtz decomposition to pressure, especially in fluid flow.⁶⁹

Oliverknill^37,69-85 highlights references related to detailed Helmholtz decomposition of the gradient and the rotational fields, considered extensively here to come up with general formalism Hamiltonian operator analysis quantum relativity. Also, mathematical matrix operational manipulations with outer and inner product space applied mathematical physics principles are listed also with^69-85 containing Dirac matrix quantum notations. Authors have adapted many techniques applied to quantum physical analysis within the framework of the quantum field theory, as well as Hermitian and non –Hermitian Hamiltonian operator quantum relativistic physics with quarternions, encountered often in these systems. Already, the reasons for applying Helmholtz decomposition fields analysis of vortex dynamics have been mentioned above, consistent with physics literature.^57,62–72 Mathematically, matrix quantum techniques with outer product of Helmholtz decomposition density field matrix are utilized to come up with eigenvector fields Hamiltonian characteristics^69-85 below.

Outer product helmholtz decomposition density field matrix eigenvector operators constructs

$|{\epsilon }_r,{\epsilon }_g>{<}_{\mu \nu }{}^{\mu \nu }|$ = ($\begin{array}{l}{\widehat{\epsilon }}_{r,\mu \nu }\\ {\widehat{\epsilon }}_{g,\mu \nu }\end{array}$$\begin{array}{l}{\widehat{\epsilon }}_g^{\mu \nu }\\ {\widehat{\epsilon }}_r^{\mu \nu }\end{array}$ )=($\begin{array}{l}{\widehat{\epsilon }}_r\\ {\widehat{\epsilon }}_g\end{array}$ )(${}_{\mu \nu }{}_{\mu \nu }$ )                                           (1)          

with ${\epsilon }_r$ : Helmholtz decomposition rotational field; ${\epsilon }_g$ : Helmholtz decomposition gradient field; ${}_{\mu \nu }{,}^{\mu \nu }$ are lower and the upper referential frame tensor calculus notations;⁶⁷ $|{\epsilon }_r,{\epsilon }_g>{<}_{\mu \nu }{}^{\mu \nu }|$ gives the outer product of both of the fields with the indices to generate 2x2 Dirac matrix forms($\begin{array}{l}{\widehat{\epsilon }}_{r,\mu \nu }\\ {\widehat{\epsilon }}_{g,\mu \nu }\end{array}$$\begin{array}{l}{\widehat{\epsilon }}_g^{\mu \nu }\\ {\widehat{\epsilon }}_r^{\mu \nu }\end{array}$ ), which is equivalent to vector forms ($\begin{array}{l}{\widehat{\epsilon }}_r\\ {\widehat{\epsilon }}_g\end{array}$ )${(}_{\mu \nu }{}^{\mu \nu }).$  Note that tensor notations fields are true for rotational and the gradient fields, permutated to the index values to have representation of both senses with rotations as well as the gradients, thereby, upward, downward, outward, & the inward field tensors are fully generalized by this format. All the matrix manipulations to achieve quantum derivations have normal techniques employed conform to those given in physics literature,^69-85 as also mentioned above.

To get eigen values of characteristic field matrix above, we equate $\left|A-\lambda I\right|=0$ ; hence

($\begin{array}{l}\epsilon r,\mu \nu -\lambda \\ \epsilon g,\mu \nu \end{array}$$\begin{array}{l}{\epsilon }_g^{\mu \nu }\\ {\epsilon }_r^{\mu \nu }-\lambda \end{array}$ )=0 & solving quadratic equation in λ:

 i.e. $({\epsilon }_{r,\mu \nu }-\lambda )({\epsilon }_r{}^{\mu \nu }- \lambda )-{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }=0$ having

${\lambda }^2–({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu }) \lambda +({\epsilon }_{r,\mu \nu }{\epsilon }_r{}^{\mu \nu }-{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })=0$ eigen values will have characteristic eigen value solutions – magnitude– general:

$\lambda =\left(1/2\right)\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })\pm {[{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })}^2–4({\epsilon }_{r,\mu \nu }{\epsilon }_r{}^{\mu \nu }-{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })]}^{1/2}\}.$ Therefore,

$\lambda =\left(1/2\right)\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })\pm {[{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }]}^{1/2}\}$       (2)

${\lambda }_1=\left(1/2\right)\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })+{[{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }]}^{1/2}\}$                  (3)

${\lambda }_2=\left(1/2\right)\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })-{[{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }]}^{1/2}\}$                                                        (4)

The diagonal elements of eigen matrix, for ${\lambda }_1$ is equivalently:

$2{\epsilon }_{r,\mu \nu }-\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })+{[{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }]}^{1/2}\}=\{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })-{\left[{\left({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu }\right)}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }\right]}^{1/2}\}$

$\left|\right|ly,2{\epsilon }_r{}^{\mu \nu }-\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })+{[{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }]}^{1/2}\}=\{(-{\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })-{\left[{\left({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu }\right)}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }\right]}^{1/2}\}$

Thus, eigenmatrix eigenvector $|{\Psi }_{i,}{}_j>$ with eigenvalue ${\lambda }_1$ :

$\left(\begin{array}{cc}0.5\{(\epsilon r,\mu \nu -{\epsilon }_r^{\mu \nu })-{[{(\epsilon r,\mu \nu -{\epsilon }_r^{\mu \nu })}^2+4\epsilon g,\mu \nu -{\epsilon }_g^{\mu \nu }]}^{0.5}& {\epsilon }_g^{\mu \nu }\\ \epsilon g,\mu \nu & 0.5\{(-\epsilon r,\mu \nu -{\epsilon }_r^{\mu \nu })-{[{(\epsilon r,\mu \nu -{\epsilon }_r^{\mu \nu })}^2+4\epsilon g,\mu \nu -{\epsilon }_g^{\mu \nu }]}^{0.5}\end{array}\right)\left(\begin{array}{l}\psi 1,1\\ \psi 1,2\end{array}\right)=0$                                                                                  (5)

Solving these equations and normalizing with respect to Φ values two eigenvectors with eigenvalue of ${\lambda }_1$ form – general:       

$\begin{array}{l}\\ {\epsilon }_g^{\mu v}\left(\begin{array}{l}\left(0.5\right\{(\epsilon r,\mu v-{\epsilon }_r^{\mu v})-\left[\right(\epsilon r,\mu v-{\epsilon }_r^{\mu v}{)}^2=4\epsilon g,\mu v-{\epsilon }_g^{\mu v}{]}^{0.5}\left]\right\}/{\epsilon }_g^{\mu v}\\ 1\end{array}\right)\end{array}$      (6.i)

${\epsilon }_{g,}\mu v\left(\begin{array}{l}1\\ \left(0.5\right\{(-\epsilon r,\mu v+{\epsilon }_r^{\mu v})-\left[\right(\epsilon r,\mu v-{\epsilon }_r^{\mu v}{)}^2=4\epsilon g,\mu v{\epsilon }_g^{\mu v}{]}^{0.5}\}/\epsilon g,\mu v\end{array}\right)$    (6.ii)

Equations (6.i) and (6.ii) together form Equation (6).

Similarly, other two eigenvectors with eigenvalue ${\lambda }_2$ form Equation (7): Equations(7.i) and (7.ii)

${\epsilon }_g\mu \nu \left(\begin{array}{l}\left(0.5\right\{(\epsilon r,\mu \nu -{\epsilon }_r^{\mu \nu })-\left\{\right(\epsilon r,\mu \nu -{\epsilon }_r^{\mu \nu }{)}^2 +4\epsilon g,\mu \nu -{\epsilon }_g^{\mu \nu }{]}^{0.5} \}/{\epsilon }_g^{\mu \nu })\\ 1\end{array}\right)$ (7.i)

${\epsilon }_g\mu \nu \left(\begin{array}{l}1\\ ({\epsilon }_g^{\mu \nu }/\epsilon r,\mu \nu {)}^{0.5}\end{array}\right)$(7.ii)

Modeling zero point & micro black hole eigen spinors protocol

Eigenvectors zero –point vector fields

Only gradient with ${\epsilon }_{g,\mu \nu }$ & ${\epsilon }_g{}^{\mu \nu }$ tensor fields expected to be active. However, ${\epsilon }_r{}^{\mu \nu }$ & ${\epsilon }_{r,\mu \nu }$ , up and down curl of the tensor fields are expected to be zero. Therefore, equation (2) will become:

$\lambda =\left(1/2\right)\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })\pm {[{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }]}^{1/2}\}=\pm {\left({\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }\right)}^{1/2}$ . That is,

${\lambda }_1={({\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })}^{1/2}$                         (8)

${\lambda }_2=-{({\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })}^{1/2}$                                                                                                                       (9)

Thus, eigenmatrix eigenvector |${\Psi }_{i,j}$  >with eigenvalue ${\lambda }_1$ :

(${(\epsilon g,\mu \nu {\epsilon }_g^{\mu \nu })}^{0.5}$ ${\epsilon }_g^{\mu \nu }$ )($\begin{array}{l}\psi 1zp\\ \psi 2zp\end{array}$ )=0

$\epsilon g,\mu \nu$ ${(\epsilon g,\mu \nu {\epsilon }_g^{\mu \nu })}^{0.5}$                                                           (10)

Two eigenvectors with eigenvalue ${\lambda }_1$ = ${({\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })}^{1/2}$ @zero –point:

${\epsilon }_g\mu \nu \left(\begin{array}{l}\text{(}\epsilon r,\mu \nu /{\epsilon }_g^{\mu \nu }{\text{)}}^{0.5}\\ 1\end{array}\right)$     (11.i)&

${\epsilon }_g\mu \nu \left(\begin{array}{l}1\\ ({\epsilon }_g^{\mu \nu }/\epsilon r,\mu \nu {)}^{0.5}\end{array}\right)$      (11.ii)

Equations (11.i) and (11.ii) together form Equation (11).

Two eigenvectors with eigenvalue ${\lambda }_2=-{({\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })}^{1/2}$ @zero –point:

${\epsilon }_g\mu \nu \left(\begin{array}{l}(-(\epsilon g,\mu \nu /{{\epsilon }_g}^{\mu \nu }{)}^{0.5}\\ 1\end{array}\right)$     (12.i)                                                     

${\epsilon }_g\mu \nu \left(\begin{array}{l}1\\ -({\epsilon }_g^{\mu \nu }/\epsilon g,\mu \nu {)}^{0.5}\end{array}\right)$ (12.ii)

Equations (12.i) and (12.ii) together form Equation (12).

Typical eigenvectors micro black hole vector fields

Only gradient with ${\epsilon }_{g,\mu \nu }$ & ${\epsilon }_g{}^{\mu \nu }$ tensor fields are expected to be zero. However, ${\epsilon }_r{}^{\mu \nu }$  & ${\epsilon }_{r,\mu \nu }$ , up and down curl of the tensor fields are expected to be active. Therefore, equation (2) will become:

$\lambda =\left(1/2\right)\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })\pm {[{({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu })}^2+4{\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu }]}^{1/2}\}=\left(1/2\right)\{({\epsilon }_{r,\mu \nu }+{\epsilon }_r{}^{\mu \nu })\pm ({\epsilon }_{r,\mu \nu }-{\epsilon }_r{}^{\mu \nu }).$ That is,

${\lambda }_1={\epsilon }_{r,\mu \nu }$                                                                                                                                                                (13)

${\lambda }_2={\epsilon }_r{}^{\mu \nu }$                                                                                                                                                                (14)

Thus, eigenmatrix eigenvector |${\Psi }_{i,j}$  >with eigenvalue ${\lambda }_1={\epsilon }_{r,\mu \nu }$ :

$\left(\begin{array}{cc}0& 0\\ 0& {\epsilon }_r^{\mu \nu }-\epsilon r,\mu \nu )\end{array}\right)\left(\begin{array}{l}\psi 1mb\\ \psi 2mb\end{array}\right)=0$                                                                                          (15)

Eigenvector with eigenvalue ${\lambda }_1={\epsilon }_{r,\mu \nu }$  @microblackhole:

($\begin{array}{l}1\\ 0\end{array}$ )                                                                                                                                                                          (16)

Similarly, eigenmatrix eigenvector |${\Psi }_{i,j}$ >with eigenvalue ${\lambda }_2={\epsilon }_r{}^{\mu \nu }$ :

$\left(\begin{array}{cc}\epsilon \text{r},\mu \nu -{\epsilon }_r^{\mu \nu }& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}\Psi 1mb\\ \Psi 2mb\end{array}\right)=0$                                                                                                                (17)

Eigenvectors with eigenvalue ${\lambda }_2={\epsilon }_r{}^{\mu \nu }$ @microblackhole:

$\left(\begin{array}{c}0\\ 1\end{array}\right)$ (18)

Hamiltonian operator eigenfields zero point gradient & microblackhole rotational eigenspinors

In zero_point (zp) Hamiltonian, H_zp, operating on wavefunction, | ${\Psi }_{zp}$ >, generating zero –point energy, $E_{zp}$ , gives:

$H_{zp}\left|{\Psi }_{zp}>=E_{zp}\right|{\Psi }_{zp}>$                                                                                                                                   (19)

Procedures with physics literature^69-85 since only sense –like fields are expected to occur in zero –point regions, with no time fields, only gradient Hamiltonian exists: $H_{zp}=icħ{\nabla }_r$     (20)

Equation (11){Equations (11.i) and (11.ii)} giving eigenvectors with ${\lambda }_{1zp}={({\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })}^{1/2}$ : 

$|{\lambda }_{1zp}>$ =($\begin{array}{l}(\epsilon g,\mu \nu {{\epsilon }_g}^{\mu \nu }{)}^{0.5}\\ {{\epsilon }_g}^{\mu \nu }\end{array}$ )                                                                                                                     (21.i)     

($\begin{array}{l}\epsilon g,\mu \nu \\ (\epsilon g,\mu \nu {{\epsilon }_g}^{\mu \nu }{)}^{0.5}\end{array}$ )                                        (21.ii)

Equations (21.i) and (21.ii) together form Equation (21).

Equations (19), (20), & (21) will give result:

$H_{zp}|{\lambda }_{1zp}>=icħ$  $\begin{array}{l}(\nabla r(\epsilon g,\mu \nu {{\epsilon }_g}^{\mu \nu }{)}^{0.5}\\ \nabla r{{\epsilon }_g}^{\mu \nu }\end{array}$ (22.i)                      

$icħ$$\begin{array}{l}\nabla r\epsilon g,\mu \nu \\ (\nabla (\epsilon g,\mu \nu {{\epsilon }_g}^{\mu \nu }{)}^{0.5}\end{array}$ (22.ii)

Equations (22.i) and (22.ii) together form Equation (22).

Performing differential algebraic manipulations, like Equation (19), having set of differential equations, for $|{\lambda }_{1zp}>=$ $\begin{array}{l}\left(\right(\epsilon g,\mu \nu {{\epsilon }_g}^{\mu \nu }{)}^{0.5}\\ {{\epsilon }_g}^{\mu \nu }\end{array}$ ) per the Equation (21), will give following equations:

$\left(icħ/2\right)[\left(\partial {\epsilon }_g{}^{\mu \nu }/\partial r\right){({\epsilon }_{g,\mu \nu }/{\epsilon }_g{}^{\mu \nu })}^{1/2}+{\left({\epsilon }_g{}^{\mu \nu }/{\epsilon }_{g,\mu \nu }\right)}^{1/2}(\partial {\epsilon }_{g,\mu \nu }/\partial r)]=E_{zp}{\left({\epsilon }_g{}^{\mu \nu }/{\epsilon }_{g,\mu \nu }\right)}^{1/2}$                  (23)

$\left(\partial {\epsilon }_g{}^{\mu \nu }/\partial r\right)=E_{zp}{\epsilon }_g{}^{\mu \nu }$                                                                                                                                        (24)

Per field –energy physics literature – listed here, we may write fields as systems 2^nd order differentials of energy, appropriately taking care of indices within the procedures; therefore,

${\epsilon }_g{}^{\mu \nu }=\left({\partial }^2{{\rm E}}_g{}^{\mu \nu }/\partial r^2\right);\left(\partial {\epsilon }_g{}^{\mu \nu }/\partial r\right)=\left({\partial }^3{{\rm E}}_g{}^{\mu \nu }/\partial r^3\right)$

${\epsilon }_{g,\mu \nu }=({\partial }^2{{\rm E}}_{g,\mu \nu }/\partial r^2);(\partial {\epsilon }_{g,\mu \nu }/\partial r)=({\partial }^3{{\rm E}}_{g,\mu \nu }/\partial r^3)$                                 (25)

Applying these equalities, and simplifying Equation (24), we can write:

$E_{ZP}=({\partial }^3{E}_{g,\mu \nu }/\partial r^3)/({\partial }^2{E}_g^{\mu \nu }/\partial r^2)$                                                                                                                 (26)

Inputting $E_{zp}$ , per the Equation (26) into Equation (8), and simplifying after multiplication with (2/icħ) ${\left({\epsilon }_g{}^{\mu \nu }/{\epsilon }_{g,\mu \nu }\right)}^{1/2},$  we obtain resulting property with partial differential equation characterizing eigenstate energetics of zero point vacuum quagmire:

$({\partial }^3{{\rm E}}_{g,\mu \nu }/\partial r^3).\left({\partial }^2{{\rm E}}_g{}^{\mu \nu }/\partial r^2\right)=\left[\left(2-icħ\right)/icħ\right]\left({\partial }^3{{\rm E}}_g{}^{\mu \nu }/\partial r^3\right).({\partial }^2{{\rm E}}_{g,\mu \nu }/\partial r^2)$                     (27)

For $|{\lambda }_1{{}^{*}}_{zp}>=$ ($\begin{array}{l}\epsilon g,\mu \nu \\ (\epsilon g,\mu \nu {\epsilon }_g^{\mu \nu }{)}^{0.5}\end{array}$ ) per the Equation (21), similar calculations applying symmetry equivalents, we will obtain result:

$({\partial }^3{E}_g^{\mu \nu }/\partial r^3).({\partial }^2{E}_{g,\mu \nu }/\partial r^2)=\left[\right(2-\text{ich})/\text{ich}]({\partial }^3{E}_{g,\mu \nu }/\partial r^3).({\partial }^2{E}_g^{\mu \nu }/\partial r^2)$       (28)

Equivalently,

${\nabla }^3{E}_g^{\mu \nu }.{\nabla }^2{E}_{g,\mu \nu }=[(2-\text{ich})/\text{ich}]{\nabla }^3{E}_{g,\mu \nu }.{\nabla }^2{E}_g^{\mu \nu }$                                                                           (29)

Similarly, ${\lambda }_{2zp}=-{({\epsilon }_{g,\mu \nu }{\epsilon }_g{}^{\mu \nu })}^{1/2}$ @zero –point will give resulting property with partial differential equations characterizing eigenstate energetics of zero point vacuum quagmire, by mathematically operating symmetry equivalents.

For $|{\lambda }_{2zp}>=$ ($\begin{array}{l}-(\epsilon g,\mu \nu {{\epsilon }_g}^{\mu \nu }{)}^{0.5}\\ {{\epsilon }_g}^{\mu \nu }\end{array}$ ) per the Equation (12) and applying Hamiltonian procedure like $|{\lambda }_{1zp}>$ above, we obtain equations:

$({\partial }^3{{\rm E}}_{g,\mu \nu }/\partial r^3).\left({\partial }^2{{\rm E}}_g{}^{\mu \nu }/\partial r^2\right)=\left[\left(2-icħ\right)/icħ\right]\left({\partial }^3{{\rm E}}_g{}^{\mu \nu }/\partial r^3\right).({\partial }^2{{\rm E}}_{g,\mu \nu }/\partial r^2)$                                                         (30)

and for $|{\lambda }_2{{}^{*}}_{zp}>=$ ($\begin{array}{l}\epsilon g,\mu \nu \\ -(\epsilon g,\mu \nu {\epsilon }_g^{\mu \nu }{)}^{0.5}\end{array}$ ) per the Equation (12) and applying Hamiltonian procedure like $|{\lambda }_1{{}^{*}}_{zp}>$ above, we obtain equations:

$\left({\partial }^3{{\rm E}}_g{}^{\mu \nu }/\partial r^3\right).({\partial }^2{{\rm E}}_{g,\mu \nu }/\partial r^2)=\left[\left(2-icħ\right)/icħ\right]({\partial }^3{{\rm E}}_{g,\mu \nu }/\partial r^3).\left({\partial }^2{{\rm E}}_g{}^{\mu \nu }/\partial r^2\right)$                       (31)

Equivalently,

${\nabla }^3{{\rm E}}_g{}^{\mu \nu }.{\nabla }^2{{\rm E}}_{g,\mu \nu }=\left[\left(2-icħ\right)/icħ\right]{\nabla }^3{{\rm E}}_{g,\mu \nu }.{\nabla }^2{{\rm E}}_g{}^{\mu \nu }$            (32)

Symmetrical nature with energy indices, with $\left[\left(2-icħ\right)/icħ\right]$  having $\approx$ value of order ${10}^{26}$ after numerically conjugating, then analytically interpreting will tell us that extremely high order energy transfers are possible at zero point, perhaps pointing to inflationary processes having quantum Diracian energy operational gradient exhibiting. One may note that if ${\epsilon }_r{}^{\mu \nu }$ & ${\epsilon }_{r,\mu \nu }$ are zero, it will imply that corresponding energy of 2^nd order derivative to be zero, pointing to the inflection of energy, that can induce consequent flow of flux due to gradient. This aspect we will notice that while analyzing micro black hole Hamiltonian values. Energy levels having order of magnitude of ${10}^{26}$  may not mean automatically that all these are one chunk, but more likely $n.m{c}^2={10}^{26}$ metric units; if m is constituting positrons & electrons, then n may be as high as order of magnitude of ${10}^{55}$ particles, the flavor mass m of particles ${10}^{-28}to{10}^{-31}$  mass units (mu) order of magnitude. These are likely progenitors’ propagators that may account for formation of plasma in star systems. These highest levels of possible inflective Diracian energies will imply possibility of infinite energy, especially with superluminal multiphase systems, that will make sense of the finite mass constraints of the real universe; subsequently, we will be investigating these in greater detail further in our ongoing work. Mathematically, one may think of these as combinatorial particles within permutational density matrix of energy source of superluminal vacuum quagmire.

We will analyze now how the sink of the energies may be constituting crucible for creation of vast majority of Standard Model particles, within context typically micro –black holes. Hamiltonian operator eigen –fields rotational eigen spinors protocol will be examined further also.

In micro –blackhole (mb) Hamiltonian, $H_{mb}$ , operating on wave function, $|{\Psi }_{mb}>$ ,generating energy, $E_{mb}$ , gives:

${{\rm H}}_{mb}\left|{\Psi }_{mb}>={{\rm E}}_{mb}\right|{\Psi }_{mb}>$                                                                                                                  (33)

Procedures perphysics literature,^69-85 for time –like fields since no space –fields are expected at micro –black hole, we consider time differential of the Hamiltonian only:

$H_{mb}=icħ\partial /\partial t$                                                                                                                                     (34)

Equation (12) will give eigenvectors with ${\lambda }_{1mb}={\epsilon }_{r,\mu \nu }$ :

$|{\lambda }_{1mb}>=$ ($\begin{array}{l}1\\ 0\end{array}$ )                                      (35)

Constructing time evolution field following physics procedures:^{65 –86}

${\epsilon }_{r,\mu \nu }\left(t\right)={\epsilon }_{r,\mu \nu ,0}{e}^{(-iHt/}{}^{ħ) }$                                                                                                                                                           (36)

Then on performing differentiation of ${\epsilon }_{r,\mu \nu }\left(t\right)$ with respect to time, we will arrive at:

$\partial {\epsilon }_{r,\mu \nu }\left(t\right)/\partial t={\epsilon }_{r,\mu \nu ,0}(-iH/ħ)e^{(-iHt/}{}^{ħ)}=(-iH/ħ){\epsilon }_{r,\mu \nu }\left(t\right)$                                                                                                 (37)

On integration with respect to time, $t=t_{i}to{t}_f$ , we get

${\displaystyle \int [\partial {\epsilon }_{r,\mu \nu }\left(t\right)/{\epsilon }_{r,\mu \nu }\left(t\right)]= }{\displaystyle \int {}_{{}_{t_i}}^{t_f}}(-iH/h) \partial t$                                                                                                               (38)

After manipulations mathematically, we arrive at:

$H=\left\{iħ/\left(t_f-t_i\right)\right\}\left[ln\left|{\epsilon }_{r,\mu \nu }\left(t\right)\right|\right]$                                                                                                                  (39)

Performing procedural relationship like in the Equation (25), we may write fields as systems of the 2^nd order differentials of energy, i.e. ${\epsilon }_{r,\mu \nu }=\left({\partial }^2{E}_{\mu \nu ,mb}/\partial r^2\right)$ , taking care of appropriate indices within the procedures as also, noting that the following relationships hold true:

${\mathbf{E}}_{\mu \nu ,\mathbf{mb}}={\iint }_r{{\epsilon }_{\mathbf{r},\mu \nu }}^{.}d\mathbf{r}$ (40)

Operating Hamiltonian per the Equations (33), (35), & (39), we can get result:

$\{{\text{ih/(t}}_{\text{f}}-{\text{t}}_{\text{i}})\}[ln\left|{\epsilon }_{{}_{r,\mu \nu }}\right|].{\epsilon }_{{}_{r,\mu \nu }}\left(\begin{array}{l}1\\ 0\end{array}\right)={\displaystyle \underset{r}{\iint }{\epsilon }_{{}_{r,\mu \nu }}}.\text{dr}{\epsilon }_{{}_{r,\mu \nu }}\left(\begin{array}{l}1\\ 0\end{array}\right)$ (41)

Partial differential operations with respect to dr performing twice, the simplified result after having multiplication throughout by

$-i\left(t_f-t_i\right)/\left\{ħ(1+ln|{\epsilon }_{r,\mu \nu }|\right\}$

$\left({\partial }^2{\epsilon }_{r,\mu \nu }/\partial r^2\right) – \left\{i\left(t_f-t_i\right)/ħ\right\}\left[{\epsilon }_{r,\mu \nu }{\left(1+ln\left|{\epsilon }_{r,\mu \nu }\right|\right]}^{-1}{\left(\partial {\epsilon }_{r,\mu \nu }/\partial r\right)}^2 +\left\{i\left(t_f-t_i\right)/ħ\right\}\right[{\epsilon }_{r,\mu \nu }/\left(1+ln\left|{\epsilon }_{r,\mu \nu }\right|\right]=0$              (42)

Equivalently,

${\nabla }^2{\epsilon }_{r,\mu \nu }–\left\{i\left(t_f-t_i\right)/ħ\right\}\left[{\epsilon }_{r,\mu \nu }{\left(1+ln\left|{\epsilon }_{r,\mu \nu }\right|\right]}^{-1}{\left(\nabla {\epsilon }_{r,\mu \nu }\right)}^2+\left\{i\left(t_f-t_i\right)/ħ\right\}\right[{\epsilon }_{r,\mu \nu }/\left(1+ln\left|{\epsilon }_{r,\mu \nu }\right|\right]=0$       (43)

Similarly, ${\lambda }_{2mb}={\epsilon }_r{}^{\mu \nu }$ @micro –black hole will give resulting property with partial differential equations characterizing eigen state rotational Hamiltonian characteristic operator time fields of micro –black hole vacuum quagmire; by mathematically operating symmetry equivalents eigen functions, Equation (18) will become:

$\left\{iħ/\left(t_f-t_i\right)\right\}\left[ln\left|{\epsilon }_r{}^{\mu \nu }\right|\right].{\epsilon }_r{}^{\mu \nu }\left(\begin{array}{c}0\\ 1\end{array}\right)={\displaystyle \underset{r}{\iint }}{\epsilon }_r{}^{\mu \nu }.dr{\epsilon }_r{}^{\mu \nu }\left(\begin{array}{c}0\\ 1\end{array}\right)$                         (44)

Partial differential operations with respect to drper forming twice, the simplified result after having multiplication throughout by $-i\left(t_f-t_i\right)/\left\{ħ(1+|ln{\epsilon }_{r,\mu \nu }|\right\}$ , we get this as the differential equation having 2^ndorder terms, for ${\lambda }_{2mb}$ @micro –black hole:

$\left({\partial }^2{\epsilon }_r{}^{\mu \nu }/\partial r^2\right)–\left\{i\left(t_f-t_i\right)/ħ\right\}\left[{\epsilon }_r{}^{\mu \nu }{\left(1+ln\left|{\epsilon }_r{}^{\mu \nu }\right|\right]}^{-1}{\left(\partial {\epsilon }_r{}^{\mu \nu }/\partial r\right)}^2 +\left\{i\left(t_f-t_i\right)/ħ\right\}\right[{\epsilon }_r{}^{\mu \nu }/\left(1+ln\left|{\epsilon }_r{}^{\mu \nu }\right|\right]=0$    (45)

Equivalently,

${\nabla }^2{\epsilon }_r{}^{\mu \nu }–\left\{i\left(t_f-t_i\right)/ħ\right\}\left[{\epsilon }_r{}^{\mu \nu }{\left(1+ln\left|{\epsilon }_r{}^{\mu \nu }\right|\right]}^{-1}{\left(\nabla {\epsilon }_r{}^{\mu \nu }\right)}^2+\left\{i\left(t_f-t_i\right)/ħ\right\}\right[{\epsilon }_r{}^{\mu \nu }/\left(1+ln\left|{\epsilon }_r{}^{\mu \nu }\right|\right]=0$       (46)

Partial differential Equations (32), (43), & (46), that were derived above justify formalism, applying tensor matrix Helmholtz decomposition fields analysis of vortex dynamics. They show that consistent quantifications are possible of magneton⁵³ experimental observations measurements verifying vortex fields to beone of the main field characteristics. Mentioned also earlier, itt is possible to transform from Helmholtz metrics, using Coulomb gage that will link to Coulomb branch gage group with Hilbert series having Super Symmetry (SUSY) Quantum Field Theory (QFT) charge conjugation.^57,70 We can then link charge conjugation to rotating charges per Dirac Maxwell Einstein Kerr Newmann metrics.^71,72 Hencethis formalism has already generality to able to model magneto –electro vacuum quanta space, that we are verifying experimentally and theoretically in our ongoing investigations.

We noted above, nature of general solutions giving eigen functions to be revealing vacuum fields energy possibly possessing higher order ${10}^{26}$ metric units at quantum zero point; these situations are analogous to situations that may be encountered at inflationary vacuum zero point, whose characteristic energies are well known in physics literature.^65–85 Based on all these, we would be able to infer that Equation (46) would be capable of giving insight through micro –black hole general solutions’ eigen value eigen functions like “fields” equations. These are too analogous to the relativistic physics with macro black holes; hence these are further extensions to micro –black holes that have been actively considered subjects within physics literature.^69-85 We can analytically quantitatively interpret with partial differential equations systems (43) & (46) these physics aspects. Especially evident while noticing, that time aspect $\left(t_f-t_i\right)$ can be quite analogous to real and proper time, with field up and down differentially spatially varying with relativistic systems. Also, notable are special requirements with rotational fields, ${\epsilon }_r$ , both up and down indices stipulating positive values due to logarithmic functionality, i.e. $ln\left|{\epsilon }_r{}^{\mu \nu }\right|$ and the apparent symmetry with 2^nd order, 1^st order, & 0^th order differential terms, per differential equations (32), (43), &(46). Special Relativity (SR) and General Relativity (GR) although prohibit the propagation of energy and information inside vacuum space with a group velocity larger than the light speed c limit, it does not impose any restrictions on the speed by which space itself can move, expand, or deform locally. Subsequently, we can deduce that its discrete quanta units uniformly consisting of all vacuum space in our Universe are not imposed by such a light speed limitation and therefore a hypothetically super –luminous phase of the vacuum space quanta is possible.⁷⁷ There are many analytical interpretations possible that are surprisingly evident, borne out of development of mathematical general solutions here, a non –assumptive pure theory primarily based on physics model of vacuum space quantum field, extendable eventually to analysis of a superluminal multiphase system that we are proposing to grand unify everything. Superluminal multiphase system models will explain all known phenomena of dark energy, dark matter, real matter, real energy with all the four fundamental forces, thus accounting totally for the enormous almost infinite energies seemingly possessed by the natural universe. Spin –offs of the superluminal multiphase systems theoretical modeling, with eventual experimental verifications, we hope may solve the problem of antimatter matter paradox of neutrino physics. Further, symmetrical aspects that we can notice with nonlinear quaternion differential equations (32), (42), & (46) above manifest vortex hydrodynamic like vacuum quanta. Our observational measurements of magneton⁵³ bears verification of these theoretical observables. Investigations by scientists spanning many international laboratories have brought out critical observations with measurements experimentally with spin ice a few salient features of mono polar possibilities, a few of which have been highlighted earlier.

 Energy fields partial differential equations

Equations (32), (43), & (46) represent fields differential equations with zero –point vacuum energy and the micro black hole field mathematical physics. One of the ways that physics can be characterized to vacuum space quanta solutions will be to input the functional form of the energy and that of field forces.

We will examine specifically vacuum fields that may follow inverse square law as well as an inverse cubic law in our subsequent paper. Typically, available physics literature shows vacuum monopoles may exhibit inverse square relation with distance, however, dipoles tend to show also an inverse cubic relation with distance. We can apply these criteria to differential equations that are developed here, i. e. Equations (32), (43), & (46) to analyze function field energy, identifying thus whether monopoles have high energy densities to initiate generation of particles within vacuum quanta; if so, then how signal output may generate in what sequences these phenomena. Performing analyses sequentially will be critical to come up with superluminal aspects, that we are currently working collaboratively with several scientists, to obtain proof of a concept hinting high energy creations, within vacuum quanta to sustain almost infinite extent universally of matter systems, manifesting geodesics as well as non –geodesics. We hope to embark on the problem –solving mathematical physics formalisms within the framework of generalized Hamiltonian operator analysis presented here, extending vacuum quanta analysis to superluminal multi phases systems modeling capable of explaining paradoxical nature with matter, antimatter, dark matter, dark energy, and the creation of stable geodesics within galactical star systems sustaining live cosmos.

Experiments, as well as measurements of real time observations of magneton by Ferrolens, reported earlier, was pointing to a fundamental vacuum quanta mechanism. The term magneton refers to elementary magnetic dipole quanta of fermions and having two joint counter rotating magnetic flux monopole vortices, forming magnetic dipole, and thus a quantum magnet. This is essentially Gilbertian having opposite magnetic charges. We propose space –time these exist only as dipoles within super luminous energy phase of “empty” vacuum space, which can phase transition to luminous or sub luminous space time, shown by schematics.

We applied Helmholtz decomposition fields with magneton experimental observations measurements showing the vortex field, reasoning that it is possible to convert from Helmholtz metrics onto Dirac –Einstein –Maxwell –Kerr –Newton metrics, by applying Coulomb gage. Ansatz generalized Hamiltonian quantum mechanics of vacuum quanta formalism was advanced here, constructing outer product Helmholtz decomposition field density matrix eigenvector operators’ Hamiltonian characteristics.

Helmholtz decomposition matrix consisted of both gradient up and down field tensors as well as the rotational up and down field tensors, that were reasoned to fit well mathematically to analyze zero –point and micro black hole in vacuum quanta. Eigen values as well as eigenvectors of characteristic general field matrix and specifically of zero –point and micro black hole eigen spinors’ vector fields were derived analytically quantitatively. Eigen matrix eigenvector $|\Psi i,j>s$ with eigen value $\lambda s$ were quantified completely mathematically. These quantifications successfully eventually generated systems partial differential equations, characterizing zero –point and microblackhole vortex and gradient energy fields of vacuum quanta.Such quantification physics techniques are quite useful in knowing as well as analyzing super luminous fabric of space aspects of vacuum quanta. This formalism has already generality to model further magneto –electro vacuum quanta space, that we are verifying in our ongoing investigations.

We hope having next set of papers on problem solving mathematical physics formalisms within well the framework of generalized Hamiltonian operator analysis, achieved here as a new ansatz, extending vacuum quanta analysis to superluminal multi phases systems modeling. This will be then capable of explaining paradoxical nature with physics, sorting quantitatively matter, antimatter, dark matter, dark energy, and the creation of stable geodesics within galactical star systems sustaining live cosmos.

None.

Author declared there are no conflicts of interest.

1. Brian Green: The fabric of the cosmos. space time and the texture of reality. Published in the United States by Alfred A. Knopf a division of Random House Inc., New York. 2004.
2. David Gross, Marc Henneaux, Alexander Sevrin. The Quantum Structure of Space and Time Proceedings of the 23rd Solvay Conference on Physics Brussels. Belgium. 2005.
3. Andrzej Horzela, Edward Kapuścik, Jarosław Kempczyński. On the Galilean Covariance of Classical Mechanics. INP No 1556/PH Kraków. 1991.
4. Tom WB Kibble, Frank H Berkshire. Classical Mechanics. 5^th 2004.
5. Richard Fitzpatrick. Maxwell’s Equations and the Principles of Electromagnetism. Infinity Science Press. 2008.
6. Anna Teresa Tymieniecka. Phenomenology of Space and Time. The Forces of the Cosmos and the Ontopoietic Genesis of Life. Book Series Analecta Husserliana. 1971 – 2018.
7. Stephen W Hawking , Roger Penrose: The Nature of Space and Time. Scientific American. 1996.
8. Hubert FM Goenner. On the History of Unified Field Theories. Living Rev Relativity. 2014;17(1):5.
9. Maya Miller. Einstein’s Greatest Theory Validated on a Galactic Scale. Scientific American. 2018.
10. Christine Sutton. Unified field theory. Physics.
11. Albert Einstein. Relativity: The Special and General Theory 1920 original. Paperback. 2010.
12. Gesche Pospiech, Marisa Michelini, Bat–Sheva Eylon. Mathematics in Physics Education.
13. Steven Weinberg. Lectures on Quantum Mechanics. 2nd edn. Cambridge University Press. 2013.
14. Matthew D Schwartz. Quantum Field Theory and the Standard Model. Cambridge University Press.2014.
15. BR Martin, G Shaw. Particle Physics.John Wiley & Sons Ltd. Publications.2008.
16. Paul Adrien Maurice Dirac. Quantised singularities in the electro vacuum field. Proc R Soc Lond. 1931;A133(821):60–72.
17. M Peskin, D Schroeder. Feynman Diagrams and Quantum Electrodynamics. An Introduction to Quantum Field Theory. West view Press. 1995. I Bialynicki Birula , Z. Bialynicka Birula. Vacuum Monopoles in the Hydrodynamic Formulation of Quantum Mechanics. Phys Rev.
18. EA Kuznetsov, VP Ruban. Hamiltonian dynamics of vortex and vacuum lines in hydrodynamic type systems. Phys Rev. 2000;61(1):831–841.
19. Kicheon Kan. Local field–interaction approach to the Dirac monopole. quant–ph. 2020.
20. Lewis A Williamson, PB Blakie. A damped point–vortex model for polar–core spin vortices in a ferro vacuum spin–1 Bose–Einstein condensate. Phys Rev Research. 2020.
21. SB Prasad, BC Mulkerin, AM Martin. Arbitrary–angle rotation of the polarization of a dipolar Bose–Einstein condensate. 2020.
22. Rajan Iyer. Observables versus observations quantum relativity operator metrics physics.
23. Rajan Iyer. Signal/Noise Analysis with Poisson Laplace Maxwell Helmholtz Mathematical Physics of Micro Black Hole Zero Point Space Time. Working Paper.
24. Aad Georges et al., Search for vacuum monopoles and stable high–electric–charge objects in 13 TeV proton–proton collisions with the ATLAS detector. Phys Rev Lett. 2020;124(3).
25. C Castelnovo, R Moessner, SL Sondhi. Vacuum monopoles in spin ice. Nature. 2008;451(7174):42–45.
26. MW Ray, E Ruokokoski, S Kandel et al. Observation of Dirac monopoles in a synthetic vacuum field. Nature. 2014;505(7485):657–660.
27. T Ollikainen, K Tiurev, A Blinova et al. Experimental Realization of a Dirac Monopole through the Decay of an Isolated Monopole. Phys Rev X. 2017;7(2):021023.
28. E Yakaboylu, A Deuchert, M.Lemeshko. Emergence of Non Abelian Vacuum Monopoles in a Quantum Impurity Problem. Physical Review Letters. 2017;119(23).
29. ST Bramwell, SR Giblin, S Calder, et al. Measurement of the charge and current of vacuum monopoles in spin ice. Nature. 2009;461(7266):956–959.
30. Giblin, ST Bramwell, D Prabhakaran, et al. Creation and measurement of long–lived vacuum monopole currents in spin ice. Nature Physics. 2011;7(3):252–258.
31. N Keswani, R Lopes, P Das, et al. Controlled creation and annihilation of stringless robust emergent vacuum monopoles in artificial spin ice. 2020.
32. Ville Pietilä, Mikko Möttönen. Creation of Dirac Monopoles in Spinor Bose Einstein Condensates. Rev. Lett. 2009;103(3):030401.
33. Elizabeth Gibney. Quantum cloud simulates vacuum monopole. Nature. 2014.
34. Chris RaDFORD. The Maxwell–Dirac Equations, Some Non–Perturbative Results. 2002;43:666–671.
35. http://128.84.4.18/pdf/2012.11370.
36. Maurice A de Gosson. The Principles of Newtonian and Quantum Mechanics. The Need for Planck's Constant h. 2nd edn. World Scientific Publishers. 2017.
37. The Helmholtz Hamiltonian System. Graph theory. Quantum Calculus. 2017.
38. Emmy Noether. Invariant Variation Problems. Transport Theory and Statistical Physics. 1(3):186–207.
39. Katherine Jones–Smith. Identifying quasi–particles using non Hermitian quantum mechanics. Philos Trans A Math Phy Eng Sci. 2013;371(1989):1–14.
40. Carl M Bender. Making sense of non–Hermitian Hamiltonians. Reports on Progress in Physics. 2007;70(6).
41. Tibor Antal, ZoltánRácz, László Sasvári. Nonequilibrium Steady State in a Quantum System: One–Dimensional Transverse Ising Model with Energy Current. Phys Rev Lett. 1997;78(2):167.
42. Ram Mehar Singh. Real Eigenvalue of a Non–Hermitian Hamiltonian System. Applied Mathematics. 2012;3:1117–1123.
43. Richard Lopp, Eduardo Martín Martínez. Quantum delocalization, gauge and quantum optics: The light–matter interaction in relativistic quantum information. quant–ph.
44. Carl M Bender. PT Symmetry: In Quantum and Classical Physics. 2019.
45. Katherine Jones Smith, Harsh Mathur. Relativistic non–Hermitian quantum mechanics. Phys Rev D. 2014:89(12).
46. Rajan Iyer: Absolute genesis fire fifth dimension mathematical physics. 2000.
47. Lisa Randall. The Boundaries of KKLT. 2020;68:3–4
48. ShamitKachru, Renata Kallosh, Andrei Linde, et al. de Sitter Vacua in String Theory. Physical Review D. 2003;68(4):046005.
49. Paul AM Dirac. The Quantum Theory of the Emission and Absorption of Radiation. Proc Roy Soc. 1927;114(767):243–265.
50. PW Milonni, ML Shih. Zero‐point energy in early quantum theory. American Journal of Physics. 1991;59(8):684–698.
51. BJ Carr, SB Giddings. Quantum Black Holes. Scientific American. 2006;292:48–55.
52. Tomohiro Nakama, Jun'ichi Yokoyama. Micro black holes formed in the early Universe and their cosmological implications. Phys Rev D. 2019;99:061303.
53. Emmanouil Markoulakis, Antonios Konstantaras, John Chatzakis, et al. Real time observation of a stationary magneton. Results in Physics, 2019;15:102793.
54. Emmanouil Markoulakis, Iraklis Rigakis, Emmanuel Antonidakis, et al. Real time visualization of dynamic vacuum fields with a nanomagnetic ferrolens. Journal of Magnetism and Magnetic Materials. 2018;451:741–748.
55. Emmanouil Markoulakis, Antonios Konstantaras, Emmanuel Antonidakis. The Quantum Field Of A Magnet Shown By A Nanovacuum Ferrolens. Journal of Magnetism and Vacuum Materials. 2018;466: 252–259.
56. Emmanouil Markoulakis, John Chatzakis, Anthony Konstantaras, et al. A synthetic macroscopic vacuum unipole. Physica Scripta. 2020;95(9):095811.
57. Kirk T McDonald. The Helmholtz Decomposition and the Coulomb Gauge. 2020.
58. MW Ray, E Ruokokoski, S Kandel, et al. Observation of Dirac monopoles in a synthetic magnetic field. Nature.2014;505:657–660
59. Omer Zor, On interactions of static magnetic fields. journal of electrical engineering. 2019;70(3):253–255.
60. The Standard Model of Particles and Interactions. Sub–nucleonic Structure and the Modern Picture of a Nucleus.
61. Sizov RA. Real magnetic charges as a negation of the electric magnetism Maxwell and electrified Dirac’s monopole. Physics & Astronomy International Journal. 2018;2(1):17–20.
62. George B Arfken, Hans J Weber. Mathematical Methods for Physicists. 6^th edn, 2005;95–101.
63. Tian Yu Cao: Conceptual Foundations of Quantum Field Theory. Cambridge University Press. 2004;179.
64. Andrew Chubykalo, Augusto Espinoza, Rolando Alvarado Flores. Helmholtz Theorems, Gauge Transformations, General Covariance and the Empirical Meaning of Gauge Conditions. Journal of Modern Physics. 2016;7:1021–1044.
65. M Casals, SR Dolan, P Kanti, et al. Angular profile of emission of non–zero spin fields from a higher–dimensional black hole. Lett. 2009;680:365–370.
66. Jean Bladel. On Helmholtz's Theorem in Finite Regions. IRE Transactions on Antennas and Propagation. 1959;7(5).
67. DC Kay. Tensor Calculus, Schaum’s Outlines. McGraw–Hill. New York. 1988.
68. Eric W Weisstein. Poincaré's Theorem From MathWorld A Wolfram Web Resource.
69. Daniel D Joseph. Helmholtz decomposition coupling rotational to irrotational flow of a viscous fluid. Proceedings of the National Academy of Sciences. 2006;103(39):14272–14277.
70. Guillermo Arias Tamargo, Antoine Bourget, Alessandro Pini, Diego Rodríguez Gómez. Discrete gauge theories of charge conjugation. Nuclear Physics B. 2019;946:114721.
71. Tim Adamoa, ET Newman. The Kerr–Newman metric: A Review. 9(10):31791.
72. Dietrich Hafner, Jean–Philippe Nicolas. Scattering of Massless Dirac Fields by a Kerr Black Hole. Reviews in Mathematical Physics. 2004;16(1):29–123.
73. Antonio Galbis, Manuel Maestre. Vector Analysis Versus Vector Calculus. 2012.
74. Loring W Tu. Vector fields –An Introduction to Manifolds. 2010;149.
75. Theresa M Korn, Granino Arthur Korn. Mathematical Handbook for Scientists and Engineers. New York. Dover Publications. 1968;157–160.
76. Clarke David A. A Primer on Tensor Calculus. 2011.
77. Francois Trèves. Topological Vector Spaces. 1967. Mineola NY Dover Publications.
78. Helmut H Schaefer, Manfred P Wolff. Topological Vector Spaces. 2^nd 1999. New York.
79. RG Lerner, GL Trigg. Encyclopaedia of Physics. 2^nd 1991.
80. S Lipschutz, M Lipson. Linear Algebra. Schaum’s Outlines 4^th 2009.
81. https://www.math.mcgill.ca/darmon/pub/Articles/Research/03.Lehmer/paper.pdf.
82. gyrovector_space oscillator_representation. Lorentz group.
83. https://quantumfrontiers.com/2018/03/27/the–math–of–multiboundary–wormholes (PDF).
84. Robert B Leighton, Matthew Sands. The Feynman Lectures on Physics. III. Reading MA. Addison–Wesley.
85. Carl D Meyer. Matrix Analysis and Applied Linear Algebra. Society for Industrial and Applied Mathematics. 2001.