The paper is based on the Galilean relativity and on a theory of cold genesis of matter and fields (CGT), which explains the gravitation and the electro-magnetic interaction by a charge model of static type, with spherical distribution of field quanta, compatible with the Fatio/LeSage model of gravitation and with the observations regarding the light beam deviation in the sun’s gravitic field. The planetary perihelion precession is explained as consequence of the dynamogene component of the gravitation force and of the high density of the sub-quantum medium, given by etheronic winds, in CGT, the electro-dynamic Lorentz’ force resulting as quantum Magnus force. It is shown that the principle of physics laws invariance may be maintained by considering also the d’Alembert paradoxe, without the conclusion of the light speed invariance, of the null rest mass of photons/bosons and of the Einsteinian speed –depending mass increasing, resulting also the possibility to explain the super-heavy astro-particles, experimentally detected, by a model of gammonic or mesonic Bose-Einstein condensate forming and pearlitizing, with the non-destructive collapsing of the formed sub-clusters, according to the cold genesis model of astroparticles of CGT.

Keywords: gravitic interaction, perihelion precession, Lorentz’ force, unitary theory, heavy astro-particles, Bose-Einstein condensate

According to a cold genesis theory of fields (CGT^1,2), the accelerating force Fe , given by repulsion between the charges Q and q, results from the impulse variation of the field quanta at the quasi-elastic collision with the semi-surface $S_x=2n{r}^2$ , i.e :

$F_r(\text{q) }={\text{ S}}_{\text{x}}\frac{\Delta {(p_c)}_r}{\Delta t}={\text{ S}}_{\text{x}}\frac{2{({\rho }_s\Delta x\cdot {\text{v}}_{\text{v}})}_r}{\Delta t}=S^0{\rho }_v\cdot {\text{v}}_{\text{v}}^{\text{2}}=q\cdot E_r(0)\text{ ; q}=\frac{S^0}{k_1}{\text{ ; S}}^{\text{0}}=4\pi \cdot r^2=\text{ n}\cdot \text{4}\pi \cdot {\text{a}}^{\text{2}}$   (1)

The electric field E is explained- in this case, by the existence of a spherically-symmetric flow of vectorial photons of the accelerating Q-charge’s field, ("vectons" – in CGT), with the impulse density: $p_v\left(0\right)={\rho }_{v}c$  –for a static interaction between Q and q, with an expression of the form:

$E_c={{\displaystyle k_1\rho }}_c(r)\cdot {\text{v}}_{\text{c}}^{\text{2}}=k_1{\rho }_a^0\frac{{{\displaystyle a}}^2}{{{\displaystyle r}}^2}\cdot {\text{v}}_{\text{c}}^{\text{2}};{\rho }_{\text{a}}^{\text{0}}={{\displaystyle \rho }}_c(a);{\text{ v}}_{\text{c}}=c;{\text{ k}}_{\text{1}}=\frac{\text{4}\pi {\text{a}}^{\text{2}}}{e}\text{; }{{\displaystyle \rho }}_c(r)={\rho }_a^0\frac{{{\displaystyle a}}^2}{{{\displaystyle r}}^2}$  (2)

i.e.- dependent on the vv- speed of quanta relative to the interaction semi-surface: $S_x=2\pi r_0{}^2=n·2\pi a^2=n{S}_x{}^0$ , of the charge q=n·e, the electric charge’s sign depending on the helicity of the vectons, (on the vecton’s spin orientation relative to the vecton’s impulse), obtained by the (pseudo)magnetic interaction with the polarized vectorial photons of the electron’s surface.^1,2 In CGT, Sx0 is considered as being the interaction section of the electron with the E-field quanta: ${S_x}^0=n{\left(a+r_v\right)}^2$, with: a=1,41fm- the radius of an electron with the e-charge on its surface and rv=0,41·a- the gauge radius of the vecton, (CGT), which results by the value of gauge constant k1 calculated by considering that- at electron’s surface (r=a), the electrostatic energy density is equal with the kinetic energy density Îv(a) of the E-field quanta, i.e.:

$\mathrm{½}{e}_0{E}^2\left(a\right)={\in }_v\left(a\right)=\mathrm{½}{\rho }_a{}^0.c^2=\mathrm{½}\left(1/k_1\right)·E\left(a\right),\Rightarrow k_1=4\pi a^2/e=S^0/e=2S_x{}^0/e$  (3)

The magnetic B-field is generated when the (pseudo)charge: qs = S0/k1 has a perpendicular $v_0=v_p.cos\theta -$ speed relative to the E-field (Figure 1), according to the impulse density theorem for ideal fluids derived from a Gauss- Ostrogranski relation, which gives the relation for the total electrodynamic force (including the Lorentz force), in the form:¹

$F_i=m_p{a}_i=\frac{S^0}{k_1}\left(k_1{\rho }_c{\text{v}}_{\text{c}}^{\text{2}}+k_1{\rho }_c{\text{v}}_{\text{c}}\text{v}{}_{\text{0}}\right)n_i={\text{q}}_{\text{s}}\left(E_i^0+B_j\cdot {\text{v}}_0\right)=F_i^0+F_i^l{\text{ ; B}}_{\text{j}}={\text{k}}_{\text{1}}{\rho }_{\text{c}}{\text{v}}_{\text{c}}\text{ ; v}{}_{\text{c}}\cong c$  (4)

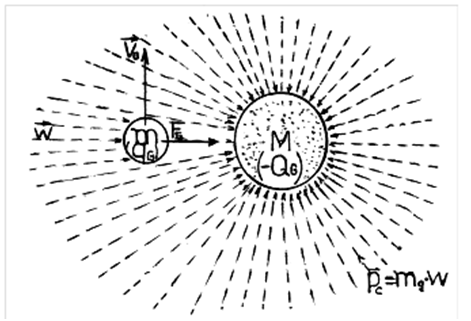
Figure 1 Gravitostatic and gravito-dynami interaction.

The eq. (4) resulting by the impulse density: $p_i=r_c{v}_c$ included in the tensor ${\prod }_{ik}$ , that is:

${{\displaystyle F}}_i={{\displaystyle m}}_p\cdot {{\displaystyle a}}_i=-\frac{d}{dt}{{\displaystyle \int }}_s{{\displaystyle \rho }}_c\cdot {{\displaystyle \text{v}}}_c\cdot d\tau =\int {{\displaystyle \Pi }}_{ik}\cdot {{\displaystyle dS}}_k$  (5)

with: ${\prod }_{ik}$ -the impulse density tensor:

${\Pi }_{ik}=P_c\cdot {\delta }_{ik}+{\rho }_c(v_i\cdot v_k);with:{\delta }_{ik}=\left(n_i{n}_k\right)=n_j;\left|n_i\right|=\left|n_k\right|=1;d{S}_k=n_{k}dS$

$(n_i;n_k-unitvectors);P_c={\rho }_c\cdot v_c^2;v_i=v_c\cdot n_i;v_k=v_0\cdot n_k\text{; }$  (6)

For ${\prod }_{ik}$ =constant and $\int d{S}_k=S^0.n_k$ , with: $S^0=4n{r}_0{}^2$  for elastic interaction with the field quanta and with:$r_0=a=e^2/8\pi {\epsilon }_0{m}_e{c}^2=1.41fm$ , (i.e the e-charge in surface), it results that: $k_1=1.57x{10}^{-10}{\left[m^2/C\right]}_{si}$ . Conform to eqn. (3), the expression of the magnetic induction results- in CGT, in the form:

$B(r)=k_1\cdot {\rho }_c{v}_v;v_v\approx c$  (7)

For the elementary electric charge ‘e’ of the electron, the charge’ sign depends on its intrinsic chirality: ${\zeta }_e$ and the magnetic moment of particles ${\mu }_p$  results in CGT from an etherono-quantonic vortex of primordial dark energy: ${\Gamma }_{\mu }={\Gamma }_A+{\Gamma }_B$ , formed by a component ${\Gamma }_A$  of ”heavy” etherons (s-etherons, $m_s\approx {10}^{-60}kg/m^3$ ), explaining physically the magnetic potential A and a component of ”quantons” (mh = hn/c2 = h·1/c2 =7.37x10-51 kg/m3), explaining physically the magnetic induction B = rot. A, generates the field lines of the induction B by the gradient of the impulse density: ${\nabla }_r{p}_A=d{p}_A/dr$ , which induces ${\zeta }_B$ -vortex-tubes of the B -induction around the vectons of the electric E- field.^1,2

The argument for a Q-charge model with sperical distribution of E-field quanta consists in the fact that an atomic proton, for example, may interact simultaneously with n electrons with the same force as in the case of the interaction with a single electron. The Maxwell’s electromagnetic field equations results in CGT according to eqs. (3)-(4), in a general vectorial form, of a vectorial E- or H- field intensity reciprocal generation:

$\overrightarrow{B}=\frac{1}{c^2}\overrightarrow{{\text{v}}_{\text{E}}}x\overrightarrow{E}$  $\overrightarrow{E^l}=\overrightarrow{{\text{v}}_{\text{0}}}x\overrightarrow{B}=-\overrightarrow{{\text{v}}_{\text{B}}}x\overrightarrow{B}$  (8)

 another specific field equation resulting also in a general way from the continuity equation:

  $\frac{\partial {{\displaystyle \rho }}_c}{\partial t}=-\nabla ({{\displaystyle \rho }}_c\cdot {\text{v}}_{\text{E}});\frac{1}{c^2}\cdot \frac{\partial ({{\displaystyle k}}_1{{\displaystyle \rho }}_c{{\displaystyle c}}^2)}{\partial t}=-\nabla ({{\displaystyle k}}_1{{\displaystyle \rho }}_c{\text{v}}_{\text{E}});\Rightarrow \frac{1}{c^2}\frac{\partial E}{\partial t}=-\nabla \cdot B=-divB$  (9)

For the electron, according to eq. (4), for r>>rm =3.86fm representing its Compton radius, the spinning of quantons in the GB-vortex around the e-charge, is realized in conditions of quantum non-equilibrium, according to the ${\Gamma }_B=2\pi r.v_{ct}=2\pi r_{m}c=ct$ , and B(r) has the vortexial kinetic moment conservation law: form found by the classic magnetism:

$B(r)={{\displaystyle k}}_1{{\displaystyle \rho }}_v{\text{v}}_{\text{ct}}^{\text{r}}\cong {{\displaystyle k}}_1{\rho }_a^0\frac{{{\displaystyle a}}^2}{{{\displaystyle r}}^2}\cdot \frac{r_{\mu }c}{r}={{\displaystyle k}}_1{{\displaystyle \rho }}_{B}c=\frac{{{\displaystyle \mu }}_{\text{0}}}{2\pi }\cdot \frac{{{\displaystyle \mu }}_e}{{{\displaystyle r}}^3};{\rho }_a^0=\frac{{{\displaystyle \mu }}_{\text{0}}}{k_1^2}\text{ ; }{{\displaystyle \rho }}_B=\frac{{\text{v}}_{\text{v}}^{\text{r}}}{\text{c}}{{\displaystyle \rho }}_v;r>{{\displaystyle r}}_{\mu };$  (10)

 ${\rho }_B–thedensityof {\zeta }_B-vortex-tubes),$ the magnetic potential resulting in the form:

$A_k(r)=\frac{B_j(r)\cdot r}{2}=\frac{k_1{r}_{\mu }c}{2}{\rho }_a^0\frac{a^2}{r^2}=\frac{k_1\cdot {\Gamma }_A(r_{\mu })}{4\pi }{\rho }_s(r)\text{; r}\ge {\text{r}}_{\mu }\text{; }{\rho }_s(r)={\rho }_a^0\frac{a^2}{r^2}\text{ ; }{\Gamma }_A(r_{\mu })=2\pi .r_{\mu }c$  (11)

Also, the Lorentz force results of Magnus type - according also to other theories,³ considering a pseudo-cylinder (barrel like) form of the electron with the high le=2a and a relative impulse density of the E-field vectons: pv= revvr, generating the B-field according to eq. (4):

$F_L=2a\cdot {\Gamma }_a^{*}\cdot n_B\cdot {\text{v}}_{\text{e}}=q\cdot B\cdot {\text{v}}_{\text{e}}=e{\zeta }_e\cdot k_1{(n_e{\text{v}}_{\text{v}}^{\text{r}})}_r\cdot {\text{v}}_{\text{e}};{\Gamma }_{\text{a}}^{\text{*}}=2\pi \cdot a\cdot c\cdot {\zeta }_e\text{; }{n}_{\text{B}}=n_e(r)\cdot [{\text{v}}_{\text{v}}^{\text{r}}/c]$  (12)

The mp-particle being formed- according to CGT, by np quantons having the mh-mass, the eq. (4) is generalisable for the gravito-dynamic force and field, by the relation: $S^0{}_g=p_p.\mathrm{½}{S}_h=\left(m_q/m_h\right).\mathrm{½}{S}_h,(S_h=4\prod r_h{}^2),$  with: rh-the quanton radius, resulted from its penetrability to the g- and s-etherons action. For the attracted mp-mass and for the gravitic field of an attractive mass M of a particle or of a body, it may be assigned an “electrogravitic” pseudo-charge, qG, respective- by eq. (4), -also an “electrogravitic” field, E_G(r,Q_G), i.e.:

$F_i^g=m_p{a}_{Gi}=q_G\cdot E_G(r,Q_G)=-k_h\cdot m_p({\rho }_g{\text{v}}_{\text{g}}^{\text{2}}+{\rho }_g⟨{\text{v}}_{\text{g}}\cdot {\text{v}}_{\text{o}}⟩)\cdot n_i\text{;}$

${\text{k}}_{\text{h}}=S_h/2m_h{\text{ q}}_{\text{G}}=S_g^0/k_1;{\text{ E}}_{\text{G}}=\pm k_1{\rho }_g{c}^2{\text{; S}}_{\text{g}}^{\text{0}}=k_h{m}_p{\text{; v}}_{\text{g}}\approx c{\text{; v}}_{\text{0}}\perp {\text{ v}}_{\text{g}}\uparrow \uparrow n_i$

In the expression (13b) of the electrogravitic field intensity, EG, the meaning of the sign:± is that the electrogravitic QG -charge generating the EG-field is given by an uniform spheric distribution of an etheronic flux with a non-compensated component, i.e. –by the difference between the received etheronic flux and the etheronic flux reflected by the super-dense centrols of the inertial M-mass structure, in the case of an attractive, gravitic M-charge.

 Therefore, considering this non-compensated etheronic component as a gravitonic field flux, having the impulse density $p_g\left(r\right)\uparrow \downarrow r$ , the generation of the gravitation force, FN , complies with the Lesage’s hypothesis⁴ which presumes the screening of the mp-mass by the M-mass in report with the cosmic etheronic winds that comes radial-symmetrically towards the M-mass, (Figure 1). The etheronic flux formed by a M-mass with disturbed sinergonic vortex which emits s-etherons, gives an antigravitic pseudocharge, generating a positive, i.e. repulsive EG-field. The gauge value of kh is obtained considering for the electron’s case the gauge condition: qG »e, which complies with the expression obtained by M. Agop,⁵ starting from the acceleration of an electron in the field of another electron:

$a_i^e=\frac{F_N^e}{m_e}+\frac{F_e^e}{m_e}=a_{Gi}^e+\left(\frac{e}{m_e}\right)\cdot \frac{e}{4\pi \epsilon \cdot r^2}=\left(\frac{e}{m_e}\right)\cdot (E_G^e(r)+E_e^e(r));{\text{ E}}_{\text{G}}^{\text{e }}=\left(\frac{m_e}{e}\right)\cdot a_{Gi}^e$ (14)

which gives by eqn. (13) the gauge values: k_h = (e/m_e)·k₁ = 27.4 [m²/kg], r_h =1.79x10^-25 m.

For the variation of ${\rho }_g\left(r\right)$ -density of the gravitonic wind, in compliance with eq. (12) of the electrogravitic qG(M)-charge of the M-mass having the radius r0 and for $v_g=c;v_0=v_p.cos\propto \perp v_g$ , the gravitic force results from eq. (12) as having the form:

$F_i^g={{\displaystyle -k}}_h{{\displaystyle m}}_p.{{\displaystyle \rho }}_g{{\displaystyle c}}^2\left(1+\frac{{\text{v}}_{\text{0}}}{\text{c}}\right){{\displaystyle n}}_i=-G\frac{{{\displaystyle m}}_{p}M}{r^2}\left(1+\frac{{\text{v}}_{\text{0}}}{\text{c}}\right){{\displaystyle n}}_i;{{\displaystyle \rho }}_g(r)={{\displaystyle \rho }}_g^{\text{0}}\frac{r_0^2}{{{\displaystyle r}}^2}\approx \frac{M}{m_h}{\rho }_g^h\frac{r_h^2}{r^2}$ (15)

Where: ${\rho }_g{}^0$  and ${\rho }_g{}^h$  are the density of the gravitonic flux (i.e.-of the uncompensed etheronic wind) at the M (r0)-mass surface and- respectively- at the mh(rh)- quanton surface.

Particularizations; the planetary perihelion precession case and the Lorentz’ force

In the case of the gravitation force, we may conclude that the force Fig given by eqn. (15) results from a potential:

$V_i{}^g\left(r\right)=V_i{}^0\left(1+v_0/c\right);(v_0=v_p{}_{\times }cos\theta //n_i).$

 If the mp-mass represents a photon having the speed v0 = c, the value of the Fig -force, acting as a gravitic type force, results from the equation (13) as being: $F^g\left(r,c\right)=2F^g\left(r,0\right),$ of a double value comparing to Newtonian static gravitational force, in accordance with the Einstein’s theory of relativity and the astrophysical observations. A form with lorentzian type term of the total gravitation force Fig , is obtained also in the tensorial theory of gravitation for a weak gravitational field, giving as solutions the gravitational analogs to Maxwell’s equations for electromagnetism,^5,6,7 the increasing of Fig with the v-speed, being equivalent with an transversal relativistic effect of the gravitational mass growth:

$F_v=g_g.m_p(1+\beta )=g_g.m_p{}^v,(\beta =v_0/c)$ (16)

We observe also that the form 15) of the total (static +dynamic) gravitation force F_i^g, for the case of a celestial body with a (quasi)constant value of v₀ corresponds: by the Kepler’s law: v₀×r=h=const., to the extended expression of the Newtonian law of gravity including an additional term, of the form:

$F_G=-(G·Mm/r^2+B·Mm/r^3),B\text{ constant}$ (17)

proposed by Newton in Newton his book: Phylosophiae naturalis Principia mathematica,attempting to explain the Moon's apsidal motion. But even if the resulted relation 13a) is compatible with the linearized form of the Einstein’s relation of general relativity in the approximation of the weak field and may explain the deviation of the light beams at the Sun’s surface, it cannot explain- in the form 13), the planetary perihelion precession without a correction, the expression of the force which may explain simultaneously the gravitational deflection of light and the planetary perihelion precession (ppp) being of the form:

$F_i^g=-G\frac{{{\displaystyle m}}_{p}M}{r^2}\left(1+\frac{{\text{v}}_{\text{0}}^{\text{2}}}{{\text{c}}^{\text{2}}}\right){{\displaystyle n}}_i;\left|n_i\right|\text{=1 }$ (18)

But the general Einsteinian relativity, even if gives verifiable quantitative results, is a geometrized theory based on transformation relations specific to the special theory of relativity, (on the light speed constancy postulate), which generated also some controversial phenomenological interpretations, such as those of the “twins paradoxe” or those of the speed- depending mass increasing to infinity at relativist speed vc. There were proposed some non-einsteinian explicative models and relations of the total gravitation force which generates the planetary perihelion precession, (Clairaut, Maillard, Bertrand, Tisserand, Lecornu, etc.). Trying a possible returning to a Galilean relativity with the re-interpretation of some experimental results¹¹ such as those of Kaufmann-Bucherer experiments by avoiding paradoxes such as those of the null rest –mass of the photon (conclusion which is in contradiction with the experimentally proven possibility of the photonic Bose- Einstein condensate producing and with the corpuscular model of photon⁹), it is raised the quescion: which phenomenon may determine the variation of the dynamogene term Fil with v02 instead a variation with v0 , in the frame of the Galilean relativity?

A plausible suggestion may result from the propose of M Fedi8 which considered a Stokes" type force as cause of the ppp phenomenon, generated by the planet"s passing with the v –speed through the superfluid physical vacuum which is considered as non-newtonian fluid, i.e.- with speed- depending viscosity, being proposed a modified Stokes"s equation for the explaining of the planetary perihelion precession, in the form:

$F_i^g=-6\pi \cdot r\cdot \eta \cdot \text{v }=\text{ - 6}\pi \cdot \text{r}\cdot \text{(}\gamma \text{ -1)}\cdot \kappa =\text{- 6}\pi \cdot \text{r}\cdot \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{1-{\left(\raisebox{1ex}{$\text{v}$}\!\left/ \!\raisebox{-1ex}{$\text{c}$}\right.\right)}^2}$}\right.-1\right)\cdot \kappa ;$ (19)

where: r – the m –body’s radius, h - the dynamic viscosity, k -unitary constant (k = 1 Kg×s-2). For the obtaining of the ppp angle during a rotation period T:

$\delta \phi =\frac{24{\pi }^3{A}^2}{T^2(1-e^2)\cdot c^2}=6\pi {\left(\frac{\text{v}}{\text{c}}\right)}^2\frac{1}{1-e^2}\approx 6\pi \frac{G(M+m)}{A(1-e^2)c^2};$ (20)

resulted by the equivalence $T^2=4{\pi }^2{a}^2/v^2$ , with A= ra –the major semi-axis and: $\text{v }=\sqrt{{\text{GM/r}}_{\text{a}}}$ the stable second cosmic velocity, is used the Taylor approximation: $2(\gamma -1)\approx {\left(v/c\right)}^2$ . We observe that the correction f(v/c) necessary in the relations 13) and 15) for concordance with the relations 18) and 19) is applied only to the dynamogene term: F_i^l and must have the form:

$f_c=f\left(v/c\right)=k_i{\left(v/c\right)}^{l}with:k_i=1;l=\left[0;1\right];$ (21)

where k_i=1 , while l = 0 only for a neglijible value of the quantum vacuum density and l=1 for a high density of the quantum vacuum, the values k_i ; l being given by the fact that the gravitation force given by the eqn. (15) at the limit: v = c is equal with those given by eqn. (18) which explains also the photonic rays bending at the sun’s surface. Equivalating similarly- in the relation 13a) of CGT, the dynamogene pseudo-lorentzian part F_i^l of the total gravitation force with a Stokes’ type force F_S^l, ${\eta }^c=\eta \left(v=c\right)$ with it results that:

$F_i^g=-k_h{m}_p\cdot {\rho }_g{c}^2\left(\frac{\text{v}}{\text{c}}\right)f_c=-6\pi \cdot r\cdot {\eta }^c{f}_c\cdot \text{v}=\text{- 6}\pi \cdot \text{r}\cdot {\left(\frac{\text{v}}{\text{c}}\right)}^2\cdot \kappa ;$  (22)

From eqn. (22) it results that the corrective factor fc must be applied to the viscosity ${\eta }^c$ . However, $\eta ={\rho }_g.v,$  (n -the kinematic viscosity) and because rg is the un-compensated component of the gravitonic (etheronic) flux $\delta {\varphi }_g$  which generates the gravitation force and n must characterize this etheronic flux, the fact that the corrective factor fc is not applied also to the static newtonian first term, Fgs, indicates that a better interpretation of the corrective factor fc may be given by the conclusion that it modify the scattering section $S_k{}^0=S^0{}_g.n_k=n_p.\mathrm{½}{S}_h\times n_k=\left(m_q/m_h\right).\mathrm{½}{S}_h,(S_h=4\pi r_h{}^2;n_k\parallel v)$ given by eqns (6) and (13b) for the limit v = c , in the sense that the etheronic flux $\delta {\varphi }_g$ but also the etheronic component of the quantum vacuum, ${\varphi }_q$ , have a laminary flow at the level of the surface $S_h{}^k=\mathrm{½}{S}_h.n_k$  of the quanton and the last component ${\varphi }_q$ – bigger than the etheronic flux dfg , generates a “screening” effect in report with the action of $\delta {\varphi }_g$ over the Shk semi-surface of the quanton, effect which is diminished with the v –speed increasing, possible- by the reciprocally compensated etheronic components ${\overline{\varphi }}_g\text{'}=-{\overline{\varphi }}_g\parallel \delta {\varphi }_g$having laminary flow at the level of Shk-surface and being parallel with the un-compensated etheronic flux $\delta {\varphi }_g$ which generates the gravitation force, the static and dynamogene forces Fl generated by the components ${\varphi }_g\text{'}=-{\varphi }_g\parallel \delta {\varphi }_g$ being reciprocally compensated. Regarding the compensated etheronic components ${\overline{\varphi }}_v\text{'}=-{\overline{\varphi }}_v\parallel \overline{v},$ we may suppose that they have a screening effect in report with the action of the $\delta {\varphi }_g$ -etheronic flux but for` $\overline{v}\parallel {\overline{\varphi }}_v,$ because the total density of their etherons is constant: $\rho ({\varphi }_v)+\rho ({\varphi }_v)=$ constant, the screening effect is also constant, explaining the fact that the corrective factor fc is not applied to the Newtonian term of the gravitation force. We may equate the previous conclusions considering in the expression 13a) of the gravitation force that the effective value of ${\rho }_g$ , generating the effective value of the gravitic force, depends to an anisotropic dynamic viscosity, ${\eta }_n=\eta \left(v_n\right);\left(n=i,j,k\right)$ in the form:

${\rho }_{ge}={\rho }_g^n=\frac{{\eta }_n}{\nu }=\frac{{\eta }^c\cdot f_c^n}{\nu }={\rho }_g^c\cdot f_c^n;{\rho }_g^c=\frac{{\eta }^c}{\nu };f_c^n={\left(\frac{v_n}{c}\right)}^l\text{; }{\eta }^c=\eta (v_n=c);l=[0,1];n=i,j,k$ (23)

in which v_n is the graviton’s speed relative to the S_n –semi-surface on which it acts. The relation 13a) of the total gravitation force for l=1 results in this case in the form:

$F_i^g=F_g^s+F_g^l=-G\frac{{{\displaystyle m}}_{p}M}{r^2}\left(f_c^i+\frac{{\text{v}}_{\text{0}}}{\text{c}}{f}_c^k\right)n_i=-G\frac{{{\displaystyle m}}_{p}M}{r^2}\left(1+\frac{{\text{v}}_{\text{0}}^{\text{2}}}{{\text{c}}^{\text{2}}}\right)n_i;f_c^i=\frac{{\text{v}}_{\text{i}}}{\text{c}}=\frac{{\text{v}}_{\text{g}}}{\text{c}}=\text{1; }{f}_c^k=\frac{{\text{v}}_{\text{k}}}{\text{c}}=\frac{{\text{v}}_{\text{0}}}{\text{c}}$  (24)

the index l=1 in the eqns (21), (23) and (24) corresponding to the mp -particle passing through a non-newtonian fluid, resulting that the index l = 0 correspons to the action of a newtonian ideal fluid. Considering that the total gravitation force FG obtained by eqns. (13), (15), (21) and (24) results from a gravitation potential VG(r) with v0 –(quasi)constant to a short time interval dt:

$V_i^g=-G\frac{{{\displaystyle m}}_{p}M}{r}\left(1+\frac{{\text{v}}_{\text{0}}^{\text{2}}}{{\text{c}}^{\text{2}}}\right);$ (25)

the effective potential V acting over a planet with the reduced mass mr in the gravitational field of the sun with the mass M, can be re-written in terms of the length a = h/c.

$V_i^g=-G\frac{m_{r}M}{r}\left(1+\frac{{\text{v}}_{\text{0}}^{\text{2}}}{{\text{c}}^{\text{2}}}\right)+m_r\frac{{\text{v}}_{\text{0}}^{\text{2}}}{\text{2}}=-\frac{m_r{c}^2}{2}\left(\frac{r_S}{r}+\frac{r_S\cdot a^2}{r^3}-\frac{a^2}{r^2}\right)$ (26)

with: $r_S=2GM/c^2$  -the Schwarzschild radius and $a=h/c;h=L/m_r=r^2(d\phi /d\tau )\approx v_0.r,$ (L -the total angular momentum of the two bodies, which is constant –according to the second Kepler’s lawr s {\displaystyle r_{s}} ), the last term being the centrifugal potential. This total potential is the same as those resulted from the Schwarzschild metric.

 Circular orbits are possible when the effective force is zero :

$F_i^g=-\frac{d{V}_i^g}{dr}=-\frac{m_r{c}^2}{2\cdot r^4}\left(r_S\cdot r+3r_S\cdot a^2-2a^{2}r\right)=\text{0}$ (27)

The precession of the planetary orbit per revolution period T resulting in the known way:

$\delta \phi =T({\omega }_{\phi }-{\omega }_r)\approx 2\pi \left(\frac{3r_S^2}{4a^2}\right)=\frac{3\pi \cdot m^2{c}^2}{2L^2}{r}_S^2\approx 6\pi \frac{G(M+m)}{A(1-e^2)c^2};{\omega }_{\text{r}}\approx {\omega }_{\phi }(1-\frac{3r_S^2}{4a^2})$ (28)

(e- the elliptic orbit’s eccentricity; $m=m_p;{\omega }_{j}T=2\pi ;a=h/c=L/m_{r}c$ ; A- the major semi-axis)

b) Even if the general relation (4) permits the deducing of the microphysical gauge expression of the magnetic induction B, it must be observed that the Lorentzian force F_i^l , in the case of interaction with an external E-field, results only for charges q composed of n elementary charges e, as consequence of the fact that the Lorentzian force is generated by the roto-activity of the electron’s surface, resulting that- without this particularity of the e-charge, i.e- for q=0, the F_i^l - force is of null value , at least to non-relativistic speeds v₀. The non-generating of a dynamogene force similar to the case of the gravitic force, may be explained by the fact that the electrostatic force is generated by a magnetic-like interaction between the vectorial photons of the E-field (“vectons”) with the vectorial photons of the e-charge’s surface (“vexons”- in CGT) and not by mechanical interaction with the electron’s surface.

Other theoretical consequences

In the absence of the action of electrical or gravitational fields, the advancement through the sub-quantum medium of a particle with relativist speed v®c, particularly- a photon, is obtained in the laminar regime and the specific drag force is of Stokes type.⁹ The approximation value of the drag force can be equated by equivalating the action of the quantum vacuum etheronic quanta with the action of some omnidirectional etheronic winds of the same mean impulse density: $p_{si}={\rho }_s·c//x$  in a point Ps in which the mp-particle is stationary. If the mp- particle will receive an impulse mp·v in a direction x-x ', by the Galilean relativity we may obtain the expression of the drag force in accordance with the expression (17) of the Stokes force, by the relation:

$F_s\left(m_{p,}v\right)=k_{h·}{f}_a·m_p\times {\rho }_s\left[{\left(c+v\right)}^2-{\left(c-v\right)}^2\right]=4f_a·k_h{m}_p.{\rho }_{s}c.v\approx 6f_a\left(m_p/m_h\right)\pi .r_c.{\rho }_s.v_s\times v$ (29)

In which: rc » 1,8x10-25m -the quanton’s calibration radius (CGT, [2]), $v_s={\eta }_v/{\rho }_s$  –the kinematic viscosity (${\eta }_v$ –the dynamic viscosity), and fa<1 - particle’s form factor, which takes into account also d’Alembert paradoxe.¹⁰ From the relation (29) it results the approximation: $v_s=\left({}^2{/}_3\right).r_c.c\approx 3,6x{10}^{-17}{m}^2/s$ .

Identifying- for the case of the interstellary space, the sub-quantum medium with the dark energy, we can take: ${\rho }_s=1.2x{10}^{-26}kg/m^3$ , resulting- to the limit: v=c, that: $a_{sM}=F_s{}^M/m_p\approx 3,31x{10}^{-8}N/kg$  - a value comparable to the gravitational acceleration generated by a mass of 1 ton at a distance of 1m, thus negligible on non-cosmic distances, compared to the terrestrial gravitational force, for example. We observe that- if the form factor fa is very small by taking into account also d’Alembert paradoxe, (~10-10–according to CGT, for concordance with the action radius of the electrostatic force¹¹), the drag force Fs is almost neglijible for a photon –for example, as in the case of a null rest-mass, and the first Newton‘s law may be considered as respected on non-cosmic distances. We may observe also that- in the einsteinian relativity, as consequence of the light speed constancy postulate and of the einsteinian formula of the speed composing, the drag force given by eqn. (29) is of null value even at very high density${\rho }_s$ of the etheronic quantum vacuum, as in the case in which the mean speed of the etheronic winds acting over a particle is the same in each point, in each direction and for each speed of the particle. So, it results that the postulate of the light speed constancy is not antagonic with the concept of ether and may be replaced with the postulate of the constancy of the etheronic winds mean speed on each direction and in each point of the space, which maintains un-changed the Newton’s laws but avoids the paradoxical conclusions of the null rest-mass of photon and of the relativist mass increasing with the speed in the Einsteinian form.¹¹ b) Another consequence of the return to the Galilean relativity is the possibility to explain without the paradoxical einsteinian hypothesis of speed-depending mass variation the astro-particles of ultra-high energy $~{10}^{17}÷{10}^{20}eV$ , recently evidenced,¹² considered as being protons or iron nuclei with r elativist speed (v®c) and increased relativist mass,¹³ emitted by some unknown physical process and which were not predicted by the Standard Model of particles.

The argument for the conclusion that the mass of an elementary particle like the electron or the proton cannot increase really until values much higher than the rest-mass of the particle may be given by the law of (matter +energy) sum conservation, analyzing two hypothetical possibilities of speed-depending mass increasing: - Classical: The increase of the intensity of the relativist etherono-quantonic vortex ${\Gamma }_r\left(v\right)$ which is generated around the (super)dense centroid(s) of the elementary particle at its passing throungh the quantum and sub-quantum vacuum ; by the condition of sub-solitons forming condition, which require that the energy of the forming vortex must be at least double than the energy of the formed mass, this mechanism, for the explaining the highest mass of some astroparticles (~1020eV) imply the existence of a value of the etherono-quantonic density of the quantum vacuum much higher than the dark energy density, in contradiction with the possibility to receive photons from far gallaxies.

Quantum: The mass increasing by the attraction of already formed neutran bosons, particularly- of „dark photons” and/or Higgs bosons from the polarised quantum vacuum, by hypothetical gluonic quanta; this hypothesis supposes a high probability to meet dark photons and/or Higgs bosons in the quantum vacuum , in contradiction with the astrophysical observations regarding the possibility to receive astroparticles with ~1020eV from far cellestial bodies. Also, the considered hypothesis imply the necessity to exists dark photons or other quantum vacuum bosons (particularly-Higgs bosons with parallel trajectory and relativist speed as those of the accelerated (astro)particle, for the possibility to explain phenomenologically the speed-depending mass variation of the relativist particle. In some previous papers of the author,^13,14 the discovered elementary particles were explained by a vortexial model, of composite fermion type, as Bose –Einstein Condensate of N gammons considered as thermalized pairs: ${\gamma }^{*}=\left(e^{-}{e}^{+}\right)$ of axially coupled electrons with opposed charges. It was argued that the particles cold forming from chiral quantum vacuum fluctuations is possible at T ®0K by already formed gammons, in a “step-by-step” process, by two possible mechanisms:

• by clusterizing, with the forming of cold preons: z0=34 me, and of basic z bosons: $z_{\pi }=7z^0;z_2=4z^0$ , with hexagonal symmetry and thereafter- of cold quarks q± and pseudo-quarks $q^0$ , by a mechanism with a first step of z*/(q±/q0)*- pre-cluster forming by magnetic interaction and a second step, of z/(q±/q0)- collapsed cluster forming , without destruction, with the aid of magnetic confinement given by residual magnetic moments mr of the clusterized gammons, which gives a superficial tension s, and:
• by pearlitizing, by the transforming of a bigger Bose-Einstein condensate of gammons or other light bosons, formed in a gravitational field of a black-hole or in a strong magnetaric-like magnetic field, into smaller gammonic clusters which may become particle-like collapsed BEC clusters by the non-destructive collapse of the gammonic BEC secondary clusters, the pearlitizing of the BEC resulting by the temperature oscillation around the equilibrium temperature TB of the initial BEC.
• The model allows the conclusion that a part of the dark matter may be formed by cold astro-particles. Some experimental arguments for the proposed model, are:

It was argued that-while the a)-mechanism explains the known elementary astroparticles, the second, b)-mechanism of particle-like collapsed cluster forming, may explain the super-heavy astroparticles of ~10²⁰eV, by a gammonic or mesonic BEC pearlitizing and non-destructive collapsing of the formed sub-clusters. For example, considering a radius r_p of meta-stable equilibrium of a drop of BEC formed by the BEC’s pearlitization and maintained by the equilibrium between the force generated by the internal vibration (thermal) energy F_t(r_p) =V×N₀k_BT_i and the force generated by the surface tension, $\sigma$:

$\frac{dE}{dr}=-P_0\frac{dV}{dr}+\sigma \frac{dS}{dr}=0\text{; V}=\frac{\text{4}\pi }{\text{3}}{r}^3\text{; S }=\text{ 4}\pi \cdot {\text{r}}^{\text{2}};$  (30)

Because $\sigma =\left(\mathrm{½}\right)F_{\gamma }/l$ , (the force rectangular on unit length), for: N₀»1/a³=3.57x10⁴⁴, (a=1.41 fm- the metastable equilibrium inter-distance between gammons¹⁴), the equilibrium radius is:

$r_p=\frac{2\sigma }{P_0}=\frac{F_{\gamma }}{l_{\gamma }\cdot P_0}\approx \frac{{\mu }_0}{2\pi \cdot l_{\gamma }}\nabla \left(\frac{{\mu }_{\gamma }^2}{d_e^3}\right){\frac{\text{1}}{{\text{N}}_{\text{0}}{k}_{B}T}}_{\text{i}}[m]$ (31)

in which d_e is the metastable equilibrium inter-distance between adjacent electronic gammons and l_g is the length of a linked gammon of the B-E condensate (BEC), for which we may approximate that: d_e» l_g » a=1.41 fm. The equality: de » a results in the gammonic z⁰, z_2, z_p clusters but also for the Cooper pairs of electrons (in superconductors), from the quasi-equality between the magnetic Vm(d) potential and the electric potential between the Cooper electrons, Ve(d) = e^*2/4ped² , for d = a, as consequence of the electric permittivity increasing: e(a)=e⁰·e^r»2e⁰ - for d»a , the refraction index depending on the quanta density at electron’ surface:¹¹

$n\left(a\right)=\left(c/vl\right)\approx \sqrt{\epsilon }r\left(a\right)~\rho c\left(a\right)~d-2=a-2;(\mu r\left(a\right)\approx 1),$

The refraction index depending on the quanta density: $n\left(a\right)=\left(c/v_l\right)\approx {\sqrt{\epsilon }}_r\left(a\right)~{\rho }_c;(m_r\left(a\right)\approx 1)$ , with ${\epsilon }_r\approx 1$ for d ³ 1.5a,¹⁴ the correlation: d = 1.5a®er » 1 resulting as consequence of the relation:

$E_{\gamma }=2m_e{c}^2=V_e\left(d_i\right)+V_{\mu }\left(d_i\right);V_{\mu }\left(d_i\right)={\mu }_r·B\left(d_i\right)\approx e^2/8\pi {\epsilon }_0·d_i;(d_i\le 1.5a)$  (32) the value: di=1.5a being specific to the hard $\gamma$ -quantum and the value $di =a$ –to the gammon.¹⁴ The expression (32) of $V_{\mu }\left(di\right)$ results in CGT by eqn. (7), because the magnetic moment radius, $r_{\mu }$, represents- in the etheronic, quantum-vortexial model of magnetic moment, the radius until which the B-field quanta have the light speed, c, and because -for di $< r\lambda =h/2mec=386$ fm, for e- -e+ interaction is maintained the relation: B= E/c , resulting that:

$B(d)=\frac{\text{E(d)}}{\text{c}}=\frac{e}{4\pi \epsilon \cdot d^{2}c}=\frac{{\mu }_0}{2\pi }\frac{{\mu }_{\text{r}}}{{\text{d}}^{\text{3}}}=\frac{{\mu }_0}{2\pi }\frac{e\cdot r_{\mu }c}{2\cdot d^3},\text{ a }\le \text{d }<{\text{ r}}_{\lambda }\text{; }\Rightarrow {\text{ r}}_{\mu }=d$ (33)

resulting –in consequence, that -at inter-distances $d \le r\lambda ,$, we have: $\mu ={\mu }_e(d/r_{\lambda }),$ with ${\mu }_e={\mu }_{PB}$ .

Inside the gammonic BEC, the metastable equilibrium interdistance between gammonic electrons: de»a corresponds –at a quantum temperature $T{e}^{\gamma }$ specific to the $\gamma$-quantum, to a mean value between the values: di = h » 0.96 fm and 1.5a =2.11 fm (which are values of un-stable, respective- of stable equilibrium, at the quantum temperature $T{e}_{\gamma }$ specific to the $\gamma$-quantum, which determine a gammonic self-resonnance). The electric interaction between gammons results as neglijible inside the gammonic BEC. Considering the correspondence with the quantum mechanics for the linking energy of the gammonic electrons, in the form (32), and approximating that- for d»a =1.41fm, l_g » a, it may be shown¹⁴that the residual magnetic potential is: $V_{\mu }\left(a\right) = {\mu }_r•B\left(a\right)\approx 1/2•E_{\gamma } = m_e{c}^2$, and –neglecting the variation of $V_{\mu }\left(d\right)$ with the temperature, the values: F_r, s and r_p have the expressions:

$F\left(a\right)=-\frac{{\text{V}}_{\mu }\text{(a)}}{\text{a}};r_p=\frac{2\sigma }{P_0}=\frac{F_{\gamma }(a)}{l_{\gamma }\cdot P_0}\approx \frac{m_e{c}^2}{a^2}{\frac{\text{1}}{{\text{N}}_{\text{0}}{k}_{B}T}}_{\text{i}}=\frac{m_e{c}^{2}a}{k_B{T}_e}=\frac{\text{8}{\text{.35x10}}^{-6}}{T_e}[m]$ (34)

resulted by the neglecting of the contribution of the electrostatic interaction force between adjacent gammons. The mass of the gammonic BEC may be approximated in this case by the relation:

$M_q=N_0{m}_p\frac{4\pi \cdot r_p^3}{3}=\frac{4\pi }{3}{m}_p{\left(\frac{{\text{m}}_{\text{e}}{c}^2}{k_B{T}_e}\right)}^{\text{3}}=\frac{m_p}{m_e}\frac{\text{0}\text{.79}}{{\text{T}}_{\text{e}}^{\text{3}}}[kg]{\text{; (m}}_{\text{p}}={\text{ m}}_{\text{e}})$ (35)

It results that- at a metastable temperature Te»1K of the gammonic BEC, for example, the mass of the gammonic cluster may be of ~ 800 g -according to eqn. (35), corresponding to a radius of ~8 mm, (comparable with the mass of a hypothetical primordial micro-“black hole, i.e : >10-5 g,¹⁶). For an exponential variation of the electron’s quantum volume density, with the mean variation radius: h»0.96 fm (CGT^1–5), the repulsive force Fr(di) of quantum disturbance, produced by “zeroth” vibrations of the electron’s super-dense kernel, corresponding to a quantum temperature Ti, is given by a quantum static pressure and a quanta density rr(di;Ti), according to a equation of static equilibrium with the residual magnetic force, resulting that the cold collapsing of the gammonic BEC is stopped at an interdistance di ~Ti between the gammonic electrons, the initial metastable equilibrium radius de$\approx$ a corresponding –at a quantum temperature Teg>Ti specific to the $\gamma -$ quantum, to a mean value between the values: di $=\eta \approx$ 0.96 fm and 1.5a =2.11 fm (which are values of un-stable, respective –of stable equilibrium, (CGT,¹⁴).

The temperature oscillation around the metastable equilibrium value Te will generate the pearlitisation of the gammonic BEC- according to the model, the formed sub-clusters resulting enough stable at T£T_e for the initiation of the cold non-destructive collapsing of the gammonic sub-cluster, according to eqns (34) and (35). The mass of the formed super-heavy particles depends on the pearlitizing temperature.

For example, for the super-heavy astro-particles of ${10}^{17}÷{10}^{20}eV,(~2x({10}^{-16}÷{10}^{-19})kg),$  the metastable temperature results of values: ${10}^5÷{10}^{6}K$  –according to eqn. (35), so a gammonic BEC with bigger mass cannot be stable formed at a such temperature. At a transition temperature TBE » 103 K, with the known relation: TBE = 3.312(ħ2/mkB)N2/3 it results as necessary an initial concentration of gammons: N » 1024 , for the transition to a gammonic BEC, which appears as stable at T<<TBE, (when $V_{\mu }\left(r\right)=\mu ·B\left(r\right)>>k_{B}T$ ).

We may suppose –en consequence, a cold forming mechanism for the super-heavy astroparticles of eV, experimentally detected, by a gammonic or mesonic BEC forming and pearlitizing, for example- at the surface of a neutronic star, particularly- of magnetar-type or even in the gravitational field of a black hole with material accretion disk around it, the escaping of the formed astro-particles from the black hole"s field being possible by the matterenergy conversion process which may generate also a pulsatory (temporary) anti-gravitic pseudo-charge of the BH star, according to CGT,^2,15 i.e- by the releasing also of the energy of etheronic vortexes (of heavy, “sinergonic” etherons) of the magnetic moments of the degenerate electrons which composes the nucleons, according to CGT, phenomenon which may explain also the large temperature variation around Te necessary for the gammonic BEC pearlitizing and the source of gammons, generated as components of destroyed z0- preons which composes the nucleonic quarks- according to the model.^13,14 It is also plausible –according to CGT, that the conversion: matter $\to$energy in the field of a BH star with accretion disk, at T$\to$1013 K, is generated by partial releasing of mesons and of component z⁰- preons, which- after the restoring of the initial value of the black hole"s gravitic charge M, may generate, in the next period, new and heavier astro-particles by clusterizing and B-E condensate forming/pearlitizing and the non-destructive collapse of the formed BEC clusters/sub-clusters.

In the case of mesons $(m_{\pi }=2z_2=8z^0\approx 272m_e;m_K\approx 2z_2+3z_{\pi }=29z^0\approx 986m_e\left(CGT\right))$  and of z0- preons (~34 me), because the eqn. (33), it results that the formed Bose-Einstein condensate is characterized by the same metastable equilibrium inter-distance (de»a) and the same expression of the meta-stable equilibrium radius, rp, (eqn. (34)) and of the B-E condensate mass, (eqn. (35)), but with mp=mp;mK or mz instead of me. We may suppose also that a gammonic or mesonic BEC formed near the metastable equilibrium temperature Te could collapse by a temperature decreasing, forming ultra-heavy particles identifiable as primordial micro- “black holes” supposed in a hot forming scenario (as products of the “Big Bang”) by Zel’dovich and Novikov in 1966 and studied in 1971 also by Stephen Hawking , which considered a inferior limit of 10−8 kg for the possibility of micro-BH forming,¹⁶ considering also their “evaporation” by the emission of Hawking radiation.

The main experimental arguments for the proposed model of astro-particles cold forming are:

1. The experimental obtaining of a BEC of photons, (a super-photon- in 2010, by a German team¹⁷)
2. The experimental evidencing of a 34me neutral boson, (cold genesis preon- in CGT), by a Hungarian team, but interpreted as quantum of a fifth force, of leptons to quarks binding,¹⁸
3. The almost same size order of the radius of scattering centers determined inside the electron and inside the nucleon, (~10-18 m19–value considered also for quarks,²⁰ but being the radius of a superdense electronic kernel, in CGT ,^1,2)
4. The producing of mesons at interaction of high energy between protons,²¹ (arguing the existence of differentiated mesonic dense kernels inside the protonic quarks, according to CGT)
5. The g-quantum splitting into a pair: e+-e- in the electric field of an atomic nucleus; (argument the existence of the repulsive field of the electronic vibrated centroids, which impede the annihilation)
6. The Cooper pair of electrons forming inside a superconductor; (argument for the er permittivity increasing for: d<1.5a, in connection with eqns. (33) and (32).

By the Galilean relativity and in the frame of a Cold Genesis of Matter and Fields (CGT) which explains the gravitation and the electro-magnetic interaction by an electric charge model of static type, with spherical distribution of field quanta, compatible with the Fatio/LeSage model of gravitation and with the observations regarding the light beam deviation in the sun"s gravitic field, the planetary perihelion precession is explained phenomenologically as consequence of the dynamogene component of the gravitation force- resulted by the use of impulse current density tensor and as consequence of the high density of the sub-quantum medium, given by etheronic winds- in CGT, which generate an interaction of the etheronic winds with the material components of the leptonic, mesonic or baryonic particles in a non-newtonian hydrodynamic regime, imposing the necessity of a corrective factor: fc=f(v/c)v/c to the dynamogene, pseudo- lorentzian part of the total gravitation force. Even if the resulted phenomenological relation for the gravitation force is not more general than the relation of the general relativity (based on the Einsteinian special relativity but considering non-inertial systems), it permits the explaining of the gravitation force generating by avoiding the conclusion of the photon"s null rest –mass, which is in contradiction with the exeperimentally obtaining of a super-photon as Bose –Einstein condensate of photons.¹⁷ In the case of electrodynamics, the Lorentz" force results as quantum Magnus force. It is shown that the principle of physics law invariance may be maintained by considering also the d"Alembert paradoxe, without the paradoxical conclusion of the light speed invariance, of the null rest mass of photons/bosons and of the Einsteinian mass increasing with the speed. It results also the possibility to explain the super-heavy astro-particles, experimentally detected, by a model of gammonic or mesonic Bose-Einstein condensate forming and pearlitizing, with the non-destructive collapsing of the formed sub-clusters, in the gravitic field of a neutronic star, particularly- of magnetar type or in the field of a black hole star with material accretion disk, i.e- by the matterenergy conversion process which may generate also a pulsatory (temporary) anti-gravitic pseudo-charge of the BH star but also mesons, z0- preons (34me) and gammons- according to CGT, considered as pairs of electrons with opposed charge, magnetically and axially coupled. Particularly, it results that- by the collapsing of the heavy gammonic or mesonic BEC by the temperature decreasing under the metastable equilibrium temperature Te, could be formed ultra-heavy particles identifiable with the considered primordial micro- black holes in a hot forming scenario.

None.

1. M Arghirescu. The Cold Genesis of Matter and Fields. 1st edn. Science PG, 2015.
2. M Arghirescu. A Quasi-Unitary Pre-Quantum theory of Particles and Fields and some Theoretical Implications. IJHEP. 2015. p. 80–103.
3. EM Kelly. Vacuum electromagnetic derived from the properties of an ideal fluid. Nuovo Cimento. 1956;11:32B.
4. Georges L Lesage. Lucrece newtonien’, Memoires de l’Academie royale des sciences et belles lettres de Berlin. Berlin. 1784. p. 1–28.
5. M Agop, C Gh Buzea, B Ciobanu. On Gravitational Shielding in Electromagnetic Fields. arXiv: physics. 1999.
6. RP Lano. Gravitational Meissner Effect. arXiv: hep-th/9603077. Phys Rev D. 1996.
7. NI Pallas, L Sofonea. Proceedings of the international congress of mathematicians. Book of International Congres of Mathematicians. Helsinki. 1978.
8. M Fedi. Physical vacuum as a dilatant fluid yields exact solutions to Pioneer anomaly and Mercury’s perihelion precession. Can J Phys. 2019;97(4):417–420.
9. M Arghirescu. A Revised Model of Photon Resulted by an Etherono-Quantonic Theory of Fields. Open Access Library Journal. 2015;2:e1920.
10. Saint-Venant A. Mémoire sur la théorie de la résistance des fluides. Solution du paradoxe proposé à ce sujet par d'Alembert aux géomètres. Comparaison de la théorie aux expériences. Comptes Rendus des Séances de l'Académie des Sciences. 1947;24:243–246.
11. M Arghirescu. Observations Concerning the Mass Variation in a Galilean - Type Relativity. IJHEP. 2018;5(1):44–54.
12. LJ Watson, DJ Mortlock, AH Jaffe. A Bayesian analysis of the 27 highest energy cosmic rays detected by the Pierre Auger Observatory. Mon Not R Astron Soc. 2011;418:206–213.
13. Hand E. Cosmic-ray theory unravels. Nature. 2010;463(7284):1011.
14. M Arghirescu. The Cold Genesis- A New Scenario of Particles Forming. PAIJ. 2017;1(5):1–5.
15. M Arghirescu, A model of particles cold forming as collapsed Bose–Einstein condensate of gammons. PAIJ. 2018;2(4):260–267.
16. M Arghirescu, L Spiridon. The Antigravitation- fiction or reality? PAIJ. 2019;3(1):19–24 .
17. S Hawking. Gravitationally collapsed objects of very low mass. Mon Not R Astron Soc. 1971;152(1):75–78.
18. D Dung, C Kurtscheid, Tobias Damm, et al. Variable potentials for thermalized light and coupled condensates. Nature Photonics. 2017;11:565–569. 
19. AJ Krasznahorkay, M Csatlós, L Csige, et al. Observation of Anomalous Internal Pair Creation in 8Be: A Possible Signature of a Light, Neutral Boson. Phys Rev Lett. 2016.
20. RD Chipman, LD Jennings. Precision pins down the electron’s magnetism. Phys Rev. 1995;132:1–3. 
21. ZEUS Collaboration. Limits on the effective quark radius from inclusive e-p scattering at HERA. Physics Letters B. 2016;757:468–472.
22. MT Ghoneim, AFH Sawy, MT Hussein. Particle production in proton-proton collisions. 2015;arXiv: 1505.06287v1.