Keeping the plasma stable throughout the plasma discharge is now considered a massive undertaking in today’s Tokamaks. In this study, the part that the current rise up phase plays in the total plasma stability was investigated, toroidal magnetic field on IR-T1 Tokamak was altered to reach the least amount of instabilities in current rise up phase. In this experiment, in order to provide rigorous and details affirmation, SVD, FFT and hard X-ray analyses were employed. The results state that with toroidal magnetic field increment to a specific amount (3.10 KV), the plasma experiences the least amount of Mirnov oscillations (almost 25%) and instabilities during current rise up phase.

Keywords: toroidal magnetic field, plasma, Mirnov oscillations, wavelengths, frequencies, array, magnetic fluctuations

Confining hot plasmas within the fusion vessel while, preventing boundaries from being destructed by the excessive heat creates an inhomogeneous state. These magnetically confined plasmas are subject to variety of linear instabilities with different wavelengths and frequencies. Plasma is normally confined in external magnetic fields. However, it doesn’t matter what the arrangements of magnetic fields are, the plasma may generate internal fields which affect its behavior. For instance, charge packing can result in E field which can cause E×B to the walls.^1,2 Tokamak plasmas are exposed to array of instabilities that contribute to known MHD modes. These instabilities are at their peak during the plasma current rise, which can be measured and identified due to their magnetic fluctuations.³ Magnetic coils called Mirnov coils are employed around the Tokamak chamber to identify the instabilities. These initial instabilities along with other forms of disruptions affect the plasma confinement and results in sudden decay of current and end of discharge. The complexity of disruptions has made them difficult to fully understand and study. It is obvious that disruptions must be avoided in Tokamak. It is mainly possible to anticipate a disruption when oscillations appear in Mirnov coils near the edge. There are some proved methods that can be helpful to prevent these disruptions especially in the current-rise phase of plasma; as a result, plasma can run smoothly throughout the wrap-up and discharge periods. In this study, in order to reduce the disruption in plasma current-rise, the toroidal magnetic field was manipulated. In the normal plasma discharge, the toroidal magnetic field is 2.85 KV, which for the sake of this experiment was changed to 3.10 KV and 2.65 KV to study the effectiveness of toroidal magnetic field on current-rise disruptions.

MHD instabilities can form and grow on flux surface with specific safety factor, which counts as the fundamental value to measure plasma instability. Safety factor (q) is defined as the number of toroidal field line that goes around the surface for one poloidal line (q=m/n). The safety factor is mainly determined by the current density profile and flux surface geometry.⁴ Current gradient and pressure gradient are the main causes of instabilities in Tokamak. Each factor results in different instability in Tokamak, the ideal mode instability and the resistive mode instability. On the other hand, magnetic fluctuations mainly occur during current-rise. At the plasma surface, the mode number “m” decreases with the association of the value of “q”. As the plasma current grow during the discharge, there is a negative current gradient at the surface which result in tearing mode to appear as the resonant surface meet the destabilizing current gradient. Mirnov oscillations of magnetic field may continue beyond the current-rise and also appear stronger at low value of “m”. Magnetic oscillation are measured by Mirnov coils and are such evidence that prove the existence of magnetic islands at the plasma surface with q=m/n.

Singular value decomposition (SVD)

The Single Value Decomposition algorithm is based on the phase difference of the signals measured by the different Mirnov coils. The SVD of our matrix W was formed as follow:

$W=VS{U}^T$

In the above expression, V is M×N orthonormal matrix (M being the channels and N data points), U is an M×M orthonormal matrix and S, is an M×M diagonal matrix.^5–8 Matlab was employed to run the relevant algorithm and the SVD and polar graphs are presented in the last section.

Fast fourier transform (FFT)

The Fast Fourier Transform (FFT) resolves a time waveform into its sinusoidal components. The FFT takes a block of time-domain data and returns the frequency spectrum of the data. The FFT is a digital implementation of the Fourier transform. FFT is representation of functions as a superposition of sinus and cosines has become widespread for both the analytic and numerical solution of deferential equations and for the analysis and treatment of communication signals.^9,10 FFT provides the range of magnetic oscillation in respect with frequency.

IR-T1 tokamak

IR-T1 Tokamak is heated through ohmic current with a circular cross section vacuum vessel made of stainless steel. It is also an air center Tokamak with major radius of R=45 cm and minor radius of 12.5 cm. IR-T1 Tokamak toroidal magnetic field is 0.9 Tesla, maximum plasma current can reach 35 KA, plasma discharge duration can last to 30 ms and electron density range is between 0.7-1.5×10¹⁹ m^-3. Table 1 provides details of IR-T1 Tokamak.^11,12

Mirnov coils

Tokamak discharges are usually rather turbulent with a large spectrum of electric and magnetic fluctuations. Mirnov oscillations are caused by rotating magnetic island inside the plasma column originated by resistive instabilities [paper]. Mirnov oscillations play an important role in the study of MHD instabilities and identifying plasma modes and safety factor. They are known to be one of the main contributors of run-away electrons generation. IR-T1 employs 12 Mirnov coils in toroidal direction with 30 degrees apart. The coils are wound on a non-magnetic former to detect plasma instabilities. Plasma contains moving charges, hence electric current, which generates flux density around itself. This varying magnetic flux density induces voltage signal in the coils, according to the Faraday's law of induction. Figure 1 illustrates the order of Mirnov coils on IR-T1 Tokamak.

Figure 1 Mirnov coils on IR-T1 Tokamak.

The basic method for determining the plasma stability is to study and analyze the plasma perturbations during the current-rise phase of discharge. In Tokamak, a considerable amount of instabilities arise from the microscopic fluctuations of the initial state. As a result, for a Tokamak to be stable during the plasma discharge, the initial state (current-rise phase) needs to run stable and fluctuation-free. In this study, in order to reduce the range of instabilities during the current rise-up, toroidal magnetic field of IR-T1 Tokamak was changed. In the first attempt, the toroidal magnetic field was amplified from 2.85 KV (of normal operating condition) to 3.10 KV and in the second attempt, the field was lowered to 2.65 KV. As can be seen from Figure 1A, when the toroidal field increased to 3.10 KV for plasma discharge, the current-rise phase ran smoothly and free of fluctuations. As it was expected, the changes in toroidal field caused the current to increase in plasma discharge after the current-rise phase. On the other hand, as the toroidal field decreased, the amount of fluctuations and instabilities rose in the current-rise phase causing the entire plasma discharge to be more unstable Figure 1B.

Figure 1A Plasma current with toroidal field 3.10 KV.

Figure 1B Plasma current with toroidal field 2.65 KV.

Plasma emits X-rays with an intensity dependent on electron temperature and density. Disruptions, can lead to sudden loss of confinement and consequently higher emission of X-rays. Figure 2 illustrates the number of photons and their intensity emitted during the changes in toroidal magnetic field. Figure 2A depicts the number and intensity of emitted energetic photons for toroidal magnetic field of 2.85 KV in respect with their energy and the current-rise phase time. As the toroidal magnetic field was lowered Figure 2B, the intensity and the number of emitted photons increased due to the increment in perturbations during current rise-up. However, as the toroidal magnetic field was amplified Figure 2C, the number of X-ray photons decreased and their intensity faded away during the current rise-up time (3-6 ms). Regarding the Mirnov oscillation, Mirnov coils were employed to measure the fluctuations in different attempts. As Figure 3A represents, when the toroidal magnetic field was reduced to 2.65 KV Figure 3B, the amplitude of MHD oscillations increased considerably, especially during the current rise-up (before 5 ms). On the contrary, when the toroidal magnetic field was set on 3.10 KV, the MHD fluctuations suppressed to nearly the noise level during the current rise-up (before 10 ms). This phenomenon may simply be the result of more powerful and stronger magnetic lines which act against the destabilizing current gradient during current rise-up. These observations are totally in agreement with plasma current graph and the X-ray emission.

Figure 2A Number of photons with respect with their energy and current-rise time for toroidal magnetic field of 2.85 KV.

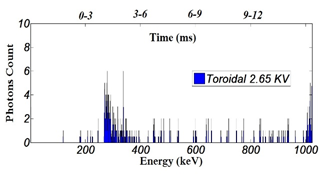
Figure 2B Number of photons with respect with their energy and current-rise time for toroidal magnetic field of 2.65 KV.

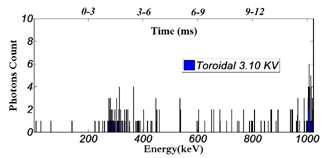
Figure 2C Number of photons with respect with their energy and current-rise time for toroidal magnetic field of 3.10 KV.

Figure 3A MHD activities with toroidal field of 2.65KV.

Figure 3B MHD activities with toroidal field of 3.10KV.

To study more details of MHD oscillations more rigorous analyses were needed. In this study, SVD analyses and polar plots of current rise-up phase in different cases were studied for a better understanding of MHD instabilities. Figure 4A,B shows the SVD and the polar plots of two time evolutions (3-4 ms and 4-6 ms respectively) when the toroidal magnetic field was 2.85 KV. The dominant plasma mode is 2-3 and some noticeable fluctuations in SVD amplitude. When the toroidal magnetic field was lowered to 2.65 KV, the SVD analyses amplitude experienced erratic fluctuations between the time evolution of 3-6 ms (peak of current-rise) and the dominant mode shifted to 3-4 as can be seen from Figure 5A and Figure 5B. As was expected, during the current rise-up for the toroidal magnetic field of 3.10 KV, the dominant mode of plasma reduced to m=1-2 and the SVD amplitude range decreased to almost noise level. This clearly shows the stability of plasma during the current rise-up phase when the toroidal field was set to 3.10 KV. Figure 6A and Figure 6B depicts the spatial and temporal structure of plasma with toroidal magnetic field of 3.10 KV.

Figure 4A Spatial and temporal structure of toroidal field 2.85 KV in 3-4 ms.

Figure 4B Spatial and temporal structure of toroidal field 2.85 KV in 4-6 ms.

Figure 5A Spatial and temporal structure of toroidal field 2.65 KV in 3-4 ms.

Figure 5B Spatial and temporal structure of toroidal field 2.65 KV in 4-6ms.

Figure 6A Spatial and temporal structure of toroidal field 3.10 KV in 3-4ms.

Figure 6B Spatial and temporal structure of toroidal field 3.10 KV in 4-6ms.

In this study the FFT analyses were also carried out on Mirnov oscillation during the toroidal magnetic field changes. FFT technique is not only a reliable analysis for plasma mode detection but it also demonstrates the dominant frequencies of Mirnov oscillations. Figure 6D shows the FFT analysis of a typical plasma discharge with toroidal field of 2.85 KV. As can be seen from the Figure, the frequency of oscillation is at its peak (almost 180) around 1200 Hz and reduces as it goes on. When the toroidal magnetic field weakened to 2.65 KV the amount of oscillation increased to above 200 for the dominant frequency in Figure 6E. However, for the toroidal magnetic field of 3.10 KV the amount of oscillation was totally suppressed at the dominant frequency Figure 6C which justify the previous results from SVD and polar graphs.

Figure 6C FFT analysis for toroidal field of 2.85 KV.

Figure 6D FFT analysis for toroidal field of 2.65 KV.

Figure 6E FFT analysis for toroidal field of 3.10 KV.

Plasma stabilities during discharge can be of vital importance in today’s Tokamaks. Minor and magnetic instabilities during current rise-up phase can play crucial roles in achieving total stability throughout the plasma discharge. In this study, with employment of SVD and FFT analyses, we managed to manipulate the toroidal magnetic field in order to suppress any excessive instabilities and magnetic fluctuations. In doing so, as the results represent, the plasma mode number decreased towards more stability during current rise up phase. Moreover, FFT graphs illustrate less Mirnov oscillation frequency when the toroidal magnetic field was set on 3.10 KV. The Mirnov oscillation decreased about 25% in FFT graph. All in all, the plasma experienced more stable current rise up phase, less hard X-ray emission, more stable mode number and less Mirnov oscillation while the toroidal magnetic field was set on 3.10 KV. As a result, the energy of the system was preserved within the Tokamak.

None.

The author declares there is no conflict of interest.

1. John Wesson. Tokamaks 3rd edn. Oxford University. 2004. p. 377.
2. JP Freidberg. Plasma Physics and Fusion Energy. Cambridge University Press. 2008.
3. DC McDonald, JG Cordey, K Thomsen, et al. Recent progress on the development and analysis of the ITPA global H-mode confinement database. Nucl Fusion. 2007;47:147.
4. TR Harley, DA Buchenauer, JW Coonrod, et al. TFTR Mirnov coil analysis with toroidal effects at plasma startup. Nucl Fusion. 1989;29:771.
5. D Raju, R jha, P K kaw, et al. Mirnov coil data analysis for tokamak ADITYA. Pramana journal of Physics. 2000;55(5–6):1–6.
6. JS Kim, DH Edgell, JM Greene. MHD mode identification of tokamak plasmas from Mirnov signals. Plasma Phys Contro. Fusion. 1999;41:1399.
7. C Nardone. Multichannel fluctuation data analysis by the singular value decomposition method. Application to MHD modes in JET. Plasma Phys Control Fusion. 1992;34(9):1–2.
8. M Ariola, A Pironti. Plasma shape control for the JET tokamak: an optimal output regulation approach. IEEE Control Systems. 2005;25(5):65–75.
9. Z Goodarzi, M Ghoranneviss, A Salar Elahi. Investigation of Tokamak Plasma MHD Activity Using FFTAnalysis of Mirnov Coils Oscillations. J Fusion Energ. 2013.
10. Tatsuoki Takeda , Shinji Tokuda. Computation of MHD equilibrium of tokamak plasma. ADS. 1991;93(1):1–107.
11. N Hasanvand, MR Riazifar, R Alipour, et al. Improving Plasma Confinement by Controlling Hard X-Ray. Chin Phys Lett. 2016;33(11):115202.
12. S Meshkani, M Ghoranneviss, M Lafouti. Effect of Biasing on Electron Temperature in IR-T1 Tokamak. Plasma Sciences (ICOPS). 2015. p. 1–25.