Rotational–translational absorption spectra of carbon dioxide, nitrogen and their mixtures with argon in the wavelength range 20–190 cm^–1 induced by pair collisions of molecules are obtained and analyzed. It is shown that, in contrast to absorption in noble gas mixtures, terahertz spectra of N₂ a CO₂ are mainly caused by quadrupole interactions, The role of the overlapping mechanism in the formation of these spectra was estimated, and the quadrupole moments of the N₂ and CO₂ molecules, equal to 1.5–1.7∙10^–26 CGSE and 4.25∙10^–26 CGS, respectively, were determined from the integrated intensity of the recorded spectra.

Keywords: terahertz spectra, collision induced absorption, quadrupole interactions, quadrupole moments of the N₂ and CO₂

The inclusion of N₂ and CO₂ molecules in the range of investigated objects makes it possible to approach the study of a wider class of interaction–induced spectra: rotational–translational spectra. In contrast to absorption in mixtures of noble gases,¹ the FIR N₂ and CO₂ spectra are mainly caused by quadrupole interactions, since the dipole moment of overlapping in the collision of two identical molecules, as well as of two identical atoms, is zero.

On the other hand, the difference between these spectra and the spectra of H₂ and its mixtures with Ar, Kr and Xe, also due to quadrupole interactions,² lies in the fact that in them the rotational part, due to the much smaller rotational constant of the molecules N₂ a CO₂ (B_N2=2cm^–1, Bco₂=0.4cm^–1, and B_H2=40cm^–1), will not be basically separated from the translational part of a, overlapping with it, forms one absorption band. The long–wavelength spectra of N₂ a CO₂ have been studied in detail in^3,4 the spectra of mixtures of these gases with Ar have been studied in less detail.⁵

The study of the spectra of their mixtures with argon, carried out in parallel with the study of the spectra of N₂ and CO₂, is interesting in that it allows us to evaluate the role of the overlapping mechanism in the formation of the rotational–translational spectrum.

The recorded absorption spectra of N₂ a CO₂ and their mixtures with argon are shown in Figure 2–7. Spectra in the 20–180 cm^–1 region were obtained using a vacuum long–wavelength spectrometer Hitachi FIS–21 with resolution of 1–2 cm^–1. The investigated mixture of gases was placed in a multi–way cell, collected according to the White scheme, with a base of 34.2 cm, which made it possible to obtain an optical layer of 6.9 m at 20 intersections of the working volume. The windows of crystalline quartz 6 mm thick were installed on a cuvette withstanding the pressure of 70 atm. Temperature regulation in the interval 135–300°K was carried out by changing the flow rate of cold nitrogen in the heat exchanger assembled on the casing. Thermal insulation was achieved by placing the cooled part of the cuvette in a vacuum.

The temperature was measured with copper–constantan thermocouple; its stability was not lower than + 2°. Gas purification was performed on a high–pressure unit assembled from absorbers with KOH and zeolite and low–temperature traps. The purity of the investigated gases was controlled by the absence of absorption in each component separately. General view of the experimental setup is shown in Figure 1.

Figure 1 General view of the experimental setup. 1–10: cleaning system, 10: multi–way cuvette, 11: long–wave infrared spectrometer, 12, 13: temperature adjustment and measurement system. PВН: systems of evacuation of a cuvette and a spectrometer.

The experimental conditions for pressures (p), density (ρ) and temperatures, and also (ν_max), (I_max) and the integrated intensities (A) of the recorded absorption bands are given in Table 1.

An analysis of the errors in the measurement and processing of the measurement results showed that the error in determining the intensities of the recorded absorption bands does not exceed 10–15%.

The first thing that attracts attention when considering these spectra is that unlike the translational spectra of noble gases and mixtures of H₂ with Ar, Kr, and Xe,² practically the entire absorption band with a maximum and wings up to a level of 5–10% with respect to absorption at the maximum. An exception is the spectra of N₂ and N₂ + Ar at room temperature, whose high–frequency wing at the boundary of the investigated range had an intensity only half the intensity at the maximum.

The spectra of CO₂ and CO₂ with argon, because of the large quadrupole moment of the CO₂ molecule, are almost an order of magnitude stronger than the spectra of N₂ and N₂ +Ar. Spectra of pure N₂ and CO₂ more intense than the spectra of the mixtures with argon. While the intensity of the spectrum of the CO₂ + Ar mixture differs several times from the intensity of the CO₂ spectrum, the intensity of the N₂ + Ar spectrum differs insignificantly from the N₂ spectrum.

This fact reflects the difference in the polarizability of CO₂ and argon: α_co2=2.93∙10^–24cm³, α_Ar=1.63∙10^–24cm³, and the proximity of the polarizability of N₂ and argon (α_N2=1.74∙10_–24cm³). In this case, as in the case of mixtures of H₂ with Ar, Kr and Xe, we are dealing here with spectra induced by the electrostatic mechanism–quadrupole induction, but in contrast to the spectra of mixtures of H₂ with Ar, Kr, and Xe in the spectra of N₂ and CO₂ and their mixtures with argon, individual rotational lines will no longer be resolved and not because of the insufficient resolution of the spectrometer$\Delta \upsilon \left(\Delta {\upsilon }_{spect}=1–2c{m}^{–1}\right)$ , but because these lines, for example, in the case of N2 from each other by 8 cm^–1,10 will be significantly broadened by the translational effect. According to,¹¹$\Delta {\nu }_J\cong 1/d\cdot \sqrt{\left(T/M\right)}$ , where d is the collision diameter, M is the reduced mass of the colliding particles. Assuming the value of d to be proportional to the value of the parameter σ of the Lennard–Jones potential, it is easy to compare it with the width of the rotational lines of H₂: for nitrogen, $\Delta {\nu }_J=40c{m}^{–1}$ , for carbon dioxide$\Delta {\nu }_J=20c{m}^{–1}$ .

The temperature behavior of the spectra is in agreement with their assignment to the rotational–translational class induced by the quadrupole field. With decreasing temperature, the spectrum shifts to the low–frequency region in accordance with the redistribution of molecules along rotational levels. It should, however, be pointed out that the maxima of the recorded absorption bands, due to the asymmetric broadening of the rotational lines, by the translational effect, are shifted to the high–frequency region with respect to those predicted by the theoretical rotational spectrum. (In Figure 2–7, the theoretical rotational spectrum is shown by vertical lines). To learn from the spectra of further information, a computer calculation of the integrated absorption intensities was carried out. From the theory of rotational–translational spectra developed by Kiss & Van Kranendonk¹², it follows that the binary absorption coefficient of a mixture of diatomic molecules with monatomic

${А}_{rot.–tr.}=\beta \cdot \{L\left(J\right)\cdot [{\lambda }^2\cdot (I+4\pi {\sigma }^2\cdot I^{\prime })+{\mu }^2\cdot (F+\frac{6mc{\sigma }^2}{i}\cdot F^{\prime })+\lambda \cdot \mu \cdot (K+\frac{7.75m{\sigma }^2}{i}\cdot K^{\prime }+D\cdot {\left({\mu }^{\prime }\right)}^2\cdot F^{\prime }\},$  (1)

where $$\beta =\frac{\pi e^2{\sigma }^3{n}_0^2}{3m{c}^2} , \text{λ}=\frac{\text{ξ}}{\text{eσ}}\cdot \text{exp}\left(-\frac{\text{σ}}{\text{ρ}}\right),\text{ μ }=\text{Q}\cdot \frac{\text{α}}{\text{eσ}5},\text{ <msup> μ <mo>′</mo> </msup> }=\sqrt{\frac{88}{255}}\cdot \frac{\gamma Q}{R^4}$$ ,and L(J) is the result of averaging over the rotational states of the molecule; I, Iʹ, F, Fʹ, K, Kʹ, and D are configuration integrals, similar to the integrals F, F′ in expression (7); Q is the quadrupole moment of the molecule; α is the polarizability; γ–anisotropy of polarizability; i is the moment of inertia.

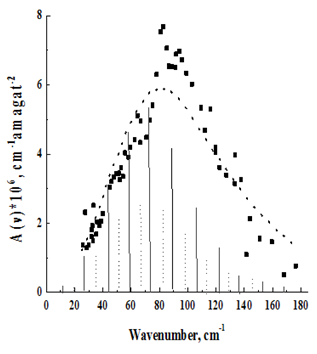
Figure 2 Rotational–translational spectrum N₂ at T=138⁰ K.

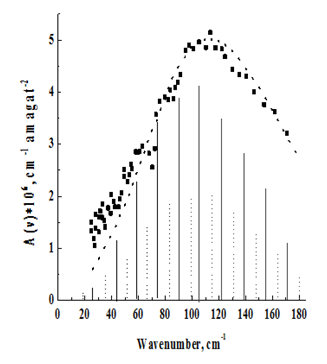
Figure 3 Rotational–translational spectrum of N₂ at T=298⁰ K.

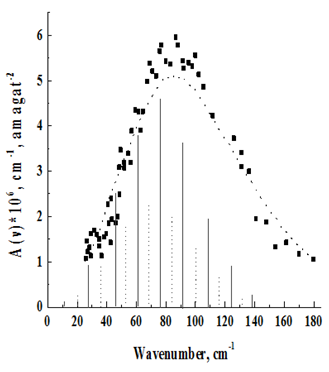
Figure 4 Rotational–translational spectrum N₂+Ar at T=138⁰ K.

Figure 5 Rotational–translational spectrum of N₂ + Ar at T=298⁰ K.

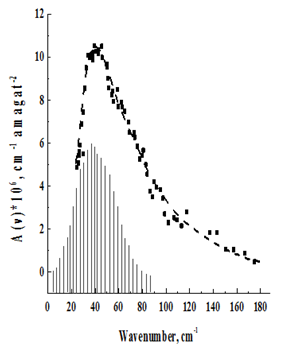
Figure 6 Rotational–translational spectrum CO₂ at T=215⁰ K.

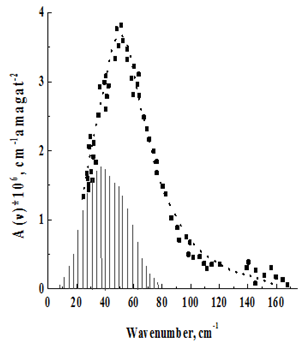
Figure 7 Rotational–translational spectrum of CO₂ + Ar at T = 215⁰ K.

The first term in (1), proportional to the integral I–is the contribution of the overlapping mechanism, the second and third, proportional to the integrals F and F', are respectively translational and rotational contributions to the spectrum due to the quadrupole induction mechanism. The terms proportional to the integrals K and K' are respectively translational and rotational contributions to the interference spectrum between the quadrupole mechanism and the overlapping mechanism. Finally, the last term, in square brackets, is the term proportional to the integral F' is the contribution of the double transitions due to the anisotropy of the polarizability: ΔJ₁=2, ΔJ₂=2 or ΔJ₁=2, ΔJ₂=0.

Since the contribution to the band is due to absorption due to quadrupole induction, according to formula (2),

${А}_{rot.}\left(J\right)=\frac{48{\pi }^4\nu }{hc}\cdot Q^2\cdot {\alpha }^2\left\{\frac{p\left(J\right)}{2J+1}- \frac{p\left(J+2\right)}{2J+5}\right\}\cdot Z\left(J,J+2\right)\cdot {\displaystyle \underset{0}{\overset{\infty }{\int }}{R}^{-6}}\cdot exp\left[–V\left(R\right)/kT\right]dR,$ (2)

where p are the Boltzmann factors and Z is the Racah`s coefficients for the quantum numbers J, V (R) is the pair interaction potential of the Lennard–Jones or Kihara type, which is obtained from (1) when only the electrostatic induction mechanism is taken into account, the relative intensities of the rotational lines of the branches S(J), O(J) and Q(J) are determined. (The branch O(J)–(transitions ΔJ=–2) corresponds to stimulated emission, which plays an important role in the formation of the total contour of the band at not too low temperatures, especially near zero frequencies. The branch Q(J)–(transitions ΔJ=0) gives a line at one frequency ν=0; however, due to broadening, its high–frequency wing must also be taken into account when calculating the total spectrum. In principle, the branch Q(J) corresponds to purely translational transitions). Each rotational line was then "broadened" on the PC and described purely formally, as in the case of spectra of mixtures of H₂ with Ar, Kr and Xe, a curve of the form:

$А(\nu )=В\cdot \nu \cdot th\left(h\nu /2kT\right)\cdot exp[–\sqrt{{\text{£}}^2+{\left(\frac{\text{ν}}{{\text{ν}}_0}\right)}^2}],$ (3)

Proposed in Kouzov¹³, The parameters of this contour B, £, and v₀ were varied so that the experimental contour was combined with the calculated one in the best way. The values ​​of B, £, and v₀, together with the values ​​of the integrated intensities found in the calculation, are given in Table 2.

Having the values ​​of the integral intensities now it is possible, if the quadrupole moments of the N₂ and CO₂ molecules are known, to assess the role of the induction mechanisms in the formation of the rotational–translational spectrum. For the N₂ molecule, the values ​​of the quadrupole moments¹ obtained by different methods differ somewhat from each other.

So, from the quantum mechanical calculations, we obtain$Q_{N2}=1.2–1.3·{10}^{–26}CGSE$ ¹⁴ obtained from the second virial coefficient and from measurements of the spin relaxation of$Q_{N2}=1.9–2.0·{10}^{–26}CGSE$ .^15,16 Intermediate values ​​were found using data on induced spectra: on the vibrational–rotational spectrum of H₂ + N₂ at: room temperature ${\mathrm{1.64.10}}^{–26}CGSE$ ;¹⁷ on the rotational–translational spectrum of N₂ at room temperature–$1.1·{10}^{–26}CGSE$ ,¹¹$1.47·{10}^{–26}CGSE$ ¹⁸ and$1.58·{10}^{–26}CGSE$ .¹⁹

We set ourselves the task, having set the induction mechanism, to determine the quadrupole moment of the N₂ molecules from the integrated intensity of the spectra recorded by us. We recall that according to (1), the following induction mechanisms take part in the formation of the rotational–translational spectrum. The first term in (1), which is proportional to the integrals I and I', is the contribution of the overlapping mechanism. The second and third terms proportional to the integrals F and F' are, respectively, translational and rotational contributions to the spectrum due to the quadrupole induction mechanism. The terms proportional to the integrals K and K' are translational and rotational contributions of the interference between the quadrupole induction mechanism and the overlapping mechanism. Finally, the last term, in parentheses, is the term proportional to the integral F', which is the contribution of the double transitions due to the anisotropy of the polarizability: ΔJ₁=2, ΔJ₂=2 or ΔJ₁=2, ΔJ₂=0.
In,^11,18,19 calculating the quadrupole moment of the N₂ molecule, it was assumed that the contribution of the overlapping mechanism to the spectrum of pure nitrogen is negligible. Indeed, in the collision of two identical particles, the coefficient characterizing the main part of the dipole moment of overlap is zero for symmetry reasons.

The contribution of transitions due to polarizability anisotropy to the total absorption intensity does not exceed, apparently, 1–2%. Thus, according to the data of,³ in the induced rotational spectrum of CO₂, the polarizability anisotropy of which is larger than for N₂, only 5% of the intensity is associated with these transitions.

Neglecting the contribution of the overlap mechanism and the contribution of the transitions due to the anisotropy of the polarizability, from (1) we obtain the following expression for the binary absorption coefficient of the rotational–translational band:

${А}_{1,rot.–tr.}.=\frac{\pi Q^2{\alpha }^2{n}_0{}^2}{c^2}\cdot L\left[\frac{F}{3m{\sigma }^7}+\frac{2F^{\text{'}}}{i{\sigma }^5}\right]$ (5)

Hence, knowing the integral intensity of the N₂ spectrum, we can determine Q_N2. Using the integrals F and F′ calculated with the Lennard–Jones potential, tabulated,^12,20 we obtain from the intensity of the N₂ spectrum at room temperature:$Q_{N2}=1.7\cdot {10}^{–26}CGSE$ , the intensity of the N₂ spectrum at T = 1380 K is $Q_{N2}=1.5\cdot {10}^{–26}CGSE$ .

In determining Q_N2 from the spectra of the N₂ + Ar mixture, the assumption of a negligible contribution of the overlapping mechanism should apparently remain in force: in the case of collision of N₂ with Ar, practically isoelectronic particles interact. If we use the correlation we found between the difference between the polarizabilities of the colliding atoms and the dipole moment parameter λ, from the graph of Figure 6 of the article²¹ with$\Delta \alpha =1.74{\left(\AA \right)}^3–1.63{\left(\AA \right)}^3=0.11{\left(\AA \right)}^3$ , we can obtain$\lambda =0.1\cdot {10}^{–4}$ . The intensity calculated for this λ is no more than 1% of the recorded absorption²>. Thus, if the overlapping mechanism is neglected, using equation (4) for the intensity of the N₂ + Ar spectrum at room temperature, we obtain$Q_{N2}=1.6\cdot {10}^{–26}CGSE$ , and from the intensity of the N₂ + Ar spectrum at$T=138{}^{0}K–Q_{N2}=1.4\cdot {10}^{–26}CGSE$ . These values are close to those obtained by other methods.

Moreover, the values determined from the low–temperature spectra of N₂ and N₂ + Ar agree better. A few overestimated values, found from spectra recorded at room temperature, seem to reflect the effect of absorbing impurities, which could not be eliminated during nitrogen purification. If we assume that the assumption of the predominant role of the quadrupole induction mechanism in the formation of the rotational–translational spectrum is also valid in the case of CO₂, calculation by formula (4), analogous to the calculation of Q_N2, leads to the following Q_CO2 values: from the induced spectrum of pure$C{O}_2–QC{O}_2=5.9\cdot {10}^{–26}CGSE$ , from the spectrum of a mixture of CO₂ with argon$–Q_{C{O}_2}=5.6\cdot {10}^{–26}CGSE$ .

These quantities, generally speaking, are close to those obtained by other authors from the rotational–translational spectrum of CO₂:$6.6–8.2\cdot {10}^{–26}CGSE$ ;²²

To clarify our calculation of$Q_{CO2}$ in terms of the intensity of the spectrum of the CO₂ + Ar mixture, we took into account the fact that this spectrum is due to its origin in addition to quadrupole induction, also the induction of overlap. Indeed, in contrast to the interaction of two isoelectronic particles of type N₂ and Ar in the collision of CO₂ and Ar, the isotropic part of the dipole moment of overlap is obviously not equal to zero. Evidence for this can be found in Bar-Ziv²⁴, in which a high–frequency wing from the center of a mixture of CO₂ + He was investigated at room temperature. It shows that in the region of 250 cm^–1, the binary absorption coefficient of the CO₂ + He mixture is only 3 times lower than in the pure CO₂ spectrum, whereas in the case of the small contribution of the overlapping mechanism it must differ in$\left(\raisebox{1ex}{${\alpha }_{СО2}$}\!\left/ \!\raisebox{-1ex}{${\alpha }_{Не}$}\right.\right) ={\left(12.5\right)}^2$ times. The intensity of the rotational–translational spectrum with allowance for the contribution of the induction of overlap is determined by the expression (1). From it, roughly estimating the graph of Figure 6 of the previous work, the parameter$\lambda ={2.10}^{–4}$ and using the integrals I, I′, F, F′, K and K′ tabulated in Poll et al.²¹ and,¹² we have:$Q_{СО2}=4.8\cdot {10}^{–26}CGSE$ .

To correct the calculation of the Q_CO2 value from the intensity of the rotational–translational spectrum of pure CO₂ as the interaction potential, instead of Lennard–Jones, the potential of Kihara was used:

$V\left(R\right)=4\epsilon \{[{(\frac{\sigma -2a}{R-2a})}^1{}^2– {(\frac{\sigma -2a}{R-2a} )}^6]\}$ (6)

with the following parameters:$\epsilon ={441.7}^0К;\sigma =3.72\AA ;2a=1.46\AA$ ,²⁶ which, as was shown in Kihara²⁷ & Datta et al.²⁸  more precisely than the Lennard–Jones potential, conveys the features of the interaction of molecules of similar CO₂.

When the Lennard–Jones potential G(R)=exp [–V(R)/ kT] is replaced by the Kihara potential, the integrals F and F¹ in expression (4) become:

$\begin{array}{l} F=336\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{-8}\cdot exp\left[ \frac{ \left(\frac{1-b}{x-b}\right){ }^6 - \left(\frac{1-b}{x-b}\right){ }^{12}}{0.25 T^{*}}\right]dx,} \\ F^1=12\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{-6}\cdot exp\left[ \frac{ \left(\frac{1-b}{x-b}\right){ }^6 - \left(\frac{1-b}{x-b}\right){ }^{12}}{0.25 T^{*}}\right]dx,}\end{array}$  (7)

where x=R / σ; b=2a / σ.

Calculating them on a PC and substituting in (4), we have obtained$Q_{CO2}=4.25·{10}^{–26}CGSE$ .

Such results indicate the prospects of studying the rotational–translational spectra of simple molecules for determining their molecular constants. The rotational–translational spectra also undoubtedly contain information about the dynamics of molecular interactions and the intermolecular potential.

The laboratory study of such spectra is also important because induced infrared absorption plays an important role in controlling the energy balance of the terrestrial atmosphere.^29,30

None.

Author declares there is no conflict of interest.

1. Birnbaum G, Krauss M, Frommhold L. Collision‐induced dipoles of rare gas mixtures. The Journal of Chemical Physics. 1984;80(6.)
2. Dunker AM, Gordon RG. Bound atom–diatomic molecule complexes. Anisotropic intermolecular potentials for the hydrogen–rare gas systems. The Journal of Chemical Physics. 1978;68(2).
3. Birnbaum WHG, Rosenberg BA. Far‐Infrared Collision‐Induced Absorption in CO2. I. Temperature Dependence. The Journal of Chemical Physics. 1971;55(3).
4. Hartmann JM, Boulet C, Jacquemart D. Molecular dynamics simulations for CO2 spectra. III. Permanent and collision–induced tensors contributions to light absorption and scattering. The Journal of Chemical Physics. 2011;134(18).
5. Kudryavtsev AA, Tonkov MV. Optics and Spectroscopy.1990; 68: 1057.
6. Sonntag RK, Crain RN. Advances in Cryogenic Engineering. 1966; 11: 379.
7. Vargaftik NB. Handbook of heat gases and liquids. Malaysia: M–Stars; 2006.
8. Malkov MP. Handbook of physical and technical sciences. Russia: M Energoatomizdat; 1985.
9. Cook D. Canadian Journal of Physics. 1957;35: 26.
10. Herzberg G. Spectra of Diatomic Molecules. USA: Van Nostrand Reinhold Company; 1951.
11. Ketelaar JAA, Hettshnick RPH. Molecular Physics. 1963;7:191.
12. Kiss ZJ, Kranendonk JV. Theory of the pressure–induced rotational spectrum of hydrogen. Canadian Journal of Physics. 1959;37(10):1187–1198.
13. Kouzov AP. Optics and Spectroscopy. 1971; 30:841.
14. Nesbet RK. Electronic Structure of N2, CO, and BF. The Journal of Chemical Physics. 1964;40(12).
15. Orcutt RH. Influence of Molecular Quadrupole Moments on the Second Virial Coefficient. The Journal of Chemical Physics. 1963; 39(3).
16. Spurling TH, Masson EA. Determination of Molecular Quadrupole Moments from Viscosities and Second Virial Coefficients. The Journal of Chemical Physics. 1967;46(1).
17. Dutta Ak. Characteristics of free electrons in graphite from a study of its magnetic and other properties. Physica. 1958;24(1–5):343–346.
18. Poll JD. Determination of the quadrupole moment of N2 from induced absorption in the far infrared. Physics Letters. 1963;7(1):32–33.
19. Dagg IR, Reesor GE, Urbaniak JL. Collision Induced Microwave Absorption in CO2 and CO2–Ar, CO2–CH4Mixtures in the 2.3 cm−1 Region. Canadian Journal of Physics. 1974;52(11): 973–978.
20. Poll JD, Kranendonk JV. Theory of translational absorption in gases. Canadian Journal of Physics. 1961; 39(1):189–204.
21. Ryzhov VA, Tonkov MV. Optics and Spectroscopy. 1974; 37:1058.
22. Harris JE. Journal of Physics. 1970;B3:704.
23. Buckingham AD, Disch RI. The quadrupole moments of dipolar molecules. Proceedings of the Royal Society. 1963;A273:275.
24. Bar–Ziv E, Weiss S. Translational Spectra Due to Collision‐Induced Overlap Moments in Mixtures of He with CO2, N2, CH4, and C2H6. The Journal of Chemical Physics. 1972;57(1).
25. Tonkov MV, Filippov NN. Optics and Spectroscopy. 1976; 41: 45.
26. Sherwood AE, Prausnits JM. Intermolecular Potential Functions and the Second and Third Virial Coefficients. The Journal of Chemical Physics. 1964;41(2).
27. Kihara T. Journal of the Physical Society of Japan. 1952;6:289.
28. Datta KK, Singh Y. Molecular Multipole Moments Determined from Viscosity and Second Virial Coefficients. The Journal of Chemical Physics. 1971;55(7).
29. Borysow A, Jurgensen UG, Zheng CG. Model atmospheres of cool, low–metallicity stars: the importance of collision–induced absorption. Astronomy & Astrophysics. 1997;324:185–195.
30. Gruszka M, Borysow A. Molecular Physics. 1998;93:1007.