Questions of application of the Vlasov model for solid state for description of the nucleation of defect structure, taking into account of the thermal conditions of the crystal growth were discussed. The Vlasov model for solid state describes the processes of complexation during the growth of real crystals adequately classical theory of nucleation and growth of second–phase particles in solids. With the help of the Vlasov model for solid state shown that during of low–temperature treatments of crystals the complexation is unlikely. In this case we have the processes of coalescence of grown–in defects. Method of calculation of the initial defect structure of crystals was proposed. This method includes the Vlasov model for solid state and the classical theory of nucleation and growth of second–phase particles in solids.

Keywords: vlasov model, crystal lattice, classical theory, nuclei

To describe the physical properties of solids in literature two approaches were suggested. In the framework of classical approach we say's about the crystal lattice.¹ The classic approach assumes: (i) location of each atom in the lattice site, (ii) the consistency of introducing the concept of probability and of the mechanical description of the behavior of particles, and (iii) the premise that the totality of atoms in a crystal is an integer. Statistical and quantum mechanical methods are used in the classical theory of the crystal. This theory has resulted to important results. In particular, one of such results is the creation of the classical theory of nucleation and growth of second–phase particles in solids.² With the help of this theory can describe the formation and development (transformation) of the defect structure of a solid, both in the process of its growth, and as a result of various technological impacts.³

The Czochralski–growth and the floating zone–growth of dislocation–free silicon monocrystals is accompanied by the formation of structural (or grown–in) microdefects. Grown–in microdefects are formed by interactions between intrinsic point defects and atoms of oxygen and carbon during crystal cooling. Grown–in microdefects are precipitates of impurities, microvoids or interstitial dislocation loops.⁴

In 2010 we publish a model of impurities high–temperature precipitation.⁵ We are theoretically describe the nucleation, growth, and coalescence of the precipitates in the range from the crystallization temperature to room temperature by introduction in formulas the dependence$T\left(t\right)$ (where$T$ is temperature,$t$ is time). The model of high–temperature precipitation is not only adequate to the experimental results of the investigation of grown–in microdefects but also does not contradict the classical theory of nucleation of second–phase particles.

In the second approach, a periodic structure of the crystal is not a consequence restriction on the freedom of movement of the atoms in the crystal. Periodic structure caused by the specificity of statistical laws of motion of particles, which agree a periodic structure with the freedom of movement of atoms. As a result the probability of finding an atom in interstitials of the crystal lattice are always different from zero.^6,7 The second approach is based on the solution of the Vlasov kinetic equation. Vlasov’s model is a system of equations for describing the evolution of the particle continuum with potential of the pair interaction.⁸ This is the task for system of many particles. Vlasov assumed that the method to solve the plasma has a universal character. The interaction in those systems can be a short–range or long–range, weak or strong.⁹

For the first time a solution for solid state was conducted Vlasov. Vlasov showed that the spatial periodic distribution is one of the particular conditions of particle motion.6,9 Such decision was conducted for the perfect crystal. Hitherto the Vlasov model for solid state has not been used.

In 2016 we publish the complexation process in accordance with Vlasov’s model for solids.¹⁰ Vlasov’s model for solids can be applied for description of structure formation of real crystal. The aim of this paper is to consider the processes of formation and growth of the particles of the second phase in the semiconductor silicon on the basis of Vlasov model for solid state and the classical theory of nucleation and growth of particles of the second phase.

The primary in Vlasov’s model is the distribution function. The particle is characterized by geometric and kinematic properties. Thus the category of motion is included on the same level with the primacy of categories of space and time. Therefore, in Vlasov model for solid state the periodic distribution of probability density of the particles is the state (motion) of the particles of the system, not the design.

The Vlasov model for solid state based on the following fundamental physical positions:^6,7 1) rejection of the principle of spatial and speed localization of the particles (in terms of classical mechanics), which takes place regardless of the force interactions; 2) introduction of force interactions in analogy with classical mechanics, but taking into account the new principle of non–localization of particles; 3) the behavior of each particle of the system is described by means of an extended in phase space$f$ –function. In this approach are combined the ideas of continuity and of corpuscular. The method of describing of motion of particle associated with the extended function, and the particle in the form of a point occurs only in the particular case.⁶

In general, the equation of Vlasov describes the evolution of the function of distribution$f\left(x,v,t\right)$ of the continuum of interacting particles in Euclidean space for speed$v$ and for coordinate$x$ at time point$t$ . Equation has the form

$\frac{\partial f}{\partial t}+\left(\frac{\partial f}{\partial x},v\right)+\left(\frac{\partial f}{\partial v},F\right)=0$  (1)

$F=-\frac{\partial }{\partial x}{\displaystyle \int K\left(x,y\right)f\left(y,v,t\right)dvdy}$

where$K$ is the pair interaction potential, which is in real problems depends on the distance$\left|x-y\right|$ ;$F$ is the total force, with which all the particles act on one of them, which is located at time$t$ at point$x$ .⁸ In order for distinguish between the types of interactions are usually talking about the systems of equations of Vlasov (Vlasov–Poisson, Vlasov–Maxwell, Vlasov–Einstein and Vlasov–Yang–Mills equations).¹¹

For a description of stationary properties of the crystal used the particles distribution density$\rho \left(r\right)={{\displaystyle \int }}^{\text{}}f\left(r,v\right)dv$ . Probable locations of atoms describes by the potential function. The potential function contains the density of probability of the particles with considering the temperature distribution of the particles.⁶ The choice of potential of the pair interaction depends on the problem under consideration. Nonlocal model of a crystal is described by nonlinear equations. These equations make it possible to calculate the molecular potential and density of location of particles in the conditions of temperature equilibrium:⁶

$V\left(r\right)=\lambda kT{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{K}_{1,2}\left(r\right)exp\left(-\frac{K_{1,2}\left(r\right)}{kT}\right)dr}$  (2)

$\rho \left(r\right)=\lambda kTexp\left(-\frac{K_{1,2}\left(r\right)}{kT}\right)$

Where$K$ is the Boltzmann constant;$K_{1,2}$ is the potential of the pair interaction;$\lambda$ is some characteristic number;$T$ is the temperature. The initial equations are equations for the two particles in a stationary condition$\left(\frac{\partial }{\partial t}=0\right)$ .6) Under the characteristic number to be understood the values of a parameter$\lambda$ , at which the Equation (2) has solutions different from the trivial.⁶ If the position of one of the particles taken as the origin of coordinates, it is possible to determine$\rho \left(0\right)=\lambda kT$ .⁶ The important task of Vlasov model for the solid state is the determination of characteristic numbers.

The characteristic number$\lambda$ is determined from the basic criterion of the existence of the crystal state. The conditions of crystallization can be written as follows:

$\frac{4\pi N}{k{T}_m}{\displaystyle \underset{0}{\overset{\infty }{\int }}{K}_{1,2}^{*}\left(\rho \right){\rho }^{2}d\rho =1}$  (3)

Where$N$ is the number of particles;$T_m$ is the temperature of melting (crystallization) of crystal;$K_{1,2}^{*}=-K_{1,2}$ .⁶ Equation (2) is written for the conditions of thermal equilibrium of system. The minima of interatomic potential correspond to the stable equilibrium position of atoms in the complexes (silicon–oxygen and silicon–carbon). Then we can determine the density of the distribution of complexes as a function of the cooling temperature of the crystal

$\rho \left(T\right)=\lambda kTexp\left(-\frac{V_{1min,2min}}{kT}\right)$  (4)

In the classical theory of nucleation and growth of new–phase particles the process of precipitation in a crystal is treated as a first–order phase transition and the kinetics of this process is divided into three stages: the formation of new–phase nuclei, the growth of clusters, and the coalescence stage.¹² The formation of new phase nuclei takes place near the crystallization front of the crystal.³ In article³ are the description of model of high–temperature precipitation of impurities. At the second stage of the precipitation process, clusters grow without a change in their number. Assuming that the precipitates have a spherical shape, it is possible to calculate the average radius of the precipitate at the growth stage:

$R\left(t\right)=\sqrt[3]{\frac{3bi\left(t\right)}{4\pi }}$  (5)

where$b$ is the quantity of order the distance between the particles in the cluster;$i\left(t\right)=\left[N\left(0\right)-N\left(t\right)\right]/N_c$ is the average number of particles at the nucleation centers;$N\left(0\right)$ is the monomer concentration at the initial instant of time;$N\left(t\right)$ is the changes in concentration of monomers over time;$N_c$ is the concentration of nucleation centers; $t$ is the time.¹³

At the third of the precipitation process, when the particles of the new phase are sufficiently large, the super saturation is relatively low, new particles are not formed and the decisive role is played by the coalescence, which is accompanied by the dissolution of small–sized particles and the growth of large–sized particles. The condition providing for changeover to the coalescence stage is the ratio$R\left(t\right)/R_{cr}\left(t\right)\approx 1$ , where$R_{cr}\left(t\right)$ is the critical radius of the precipitate. Under this condition, the precipitate is in equilibrium with the solution$\left(dR/dt=0\right)$ . The precipitate grows at$R\left(t\right)>R_{cr}\left(t\right)$ and dissolves at$R\left(t\right)<R_{cr}\left(t\right)$ . With time, the critical radius$R_{cr}\left(t\right)$ increases and the number of particles per unit volume decreases.^13,14

Is possible to determine the critical size of the precipitates in accordance with:¹⁵
$R_{cr}^O\left(t\right)=\frac{2\sigma u{V}_p}{kT\left(t\right)\ln (S_0{S}_i^{-{\gamma }_i}{S}_v^{{\gamma }_v})-6\mu \delta \epsilon u{V}_p}$

$R_{cr}^C\left(t\right)=\frac{2\sigma u{V}_p}{kT\left(t\right)\ln (S_{с}{S}_i^{{\gamma }_i}{S}_v^{-{\gamma }_v})-6\mu \delta \epsilon u{V}_p}$ (6)

where$S_o=\raisebox{1ex}{$C_o$}\!\left/ \!\raisebox{-1ex}{$C_o^{eg}$}\right.,S_c=\raisebox{1ex}{$C_c$}\!\left/ \!\raisebox{-1ex}{$C_c^{eg}$}\right.,S_i=\raisebox{1ex}{$C_i$}\!\left/ \!\raisebox{-1ex}{$C_i^{eg}$}\right.,S_v=\raisebox{1ex}{$C_v$}\!\left/ \!\raisebox{-1ex}{$C_v^{eg}$}\right.$ are the supersaturations of the oxygen atoms, carbon atoms, intrinsic interstitial silicon atoms, and vacancies, respectively;$\sigma$ is the density of the surface energy of the interface between the precipitate and the matrix;$\mu$ is the shear modulus of silicon;$\delta$ and$\epsilon$ are the linear and volume misfit strains of the precipitate and the matrix, respectively;${\gamma }_i$ and${\gamma }_v$ are the fractions of intrinsic interstitial silicon atoms and vacancies per impurity atom attached to the precipitate, respectively;$V_p$ is the molecular volume of the precipitate; and $u={(1+{\gamma }_{i}x+{\gamma }_{v}x)}^{-1}\cdot {(\frac{1+\epsilon }{1+\delta })}^3$ .

The average size of precipitates at the stage of the coalescence is proportional to the cube root of time:¹³

$R_{av}(t)=\sqrt[3]{R_{cr}^3\left(t_0\right)+\frac{4D\beta t}{9}}$  (7)

where$D$ is the diffusion coefficient of impurity atoms;$\beta =\left(\frac{\sigma \Omega }{kT}\right)N\left(0\right)$ ;$R_{cr}\left(t_0\right)$ is the initial critical radius;$\sigma$ is the surface tension at the precipitate–solid solution interface;$\Omega$ is the atomic volume.

As is known, the formation and development of the structure of grown–in microdefects in silicon are determined by thermal conditions of growth and cooling of the crystal.^3,4 The temperature distribution along the length of the ingot during its cooling varies depending on the thermal parameters of the growth according to the expression$1/T=1/T_m+Gz/T_m^2$ , where$z$ is the distance from the crystallization front;$G$ is the axial temperature gradient at the crystallization front;$T_m$ is the crystallization temperature.³ It should be noted that, in the general case, it is necessary to take into account the radial in homogeneity of the temperature field. We introduce the crystal growth rate ($V$ ) into in this formula and obtain

$T\left(t\right)=\frac{T_m^2}{T_m+VGt}$ (8)

We performed three separate groups of calculations that simulated the processes of precipitation during the growth of crystals of large and small diameters with the use of the Czochralski method (CZ–Si) and crucibleless floating zone melting (FZ–Si). Calculations of the first group (I) was performed using the following parameters: the crystal growth rate was$V=0.6 mm/min$ , the axial temperature gradient was$N_c$ , the oxygen concentration was$N\left(0\right)={10}^{18}c{m}^{-3}$ , and the carbon concentration was$N\left(0\right)={10}^{18}c{m}^{-3}$ . The corresponding parameters used in calculations of the second group (II) were as follows: the crystal growth rate was $V=0.3 mm/min$ , the axial temperature gradient was $G=25K/сm$ , the oxygen concentration was$N\left(0\right)={10}^{18}c{m}^{-3}$ , and the carbon concentration was$N\left(0\right)={10}^{18}c{m}^{-3}$ . These conditions correspond to the growth of large–sized silicon single crystals with the use of the Czochralski method. For calculations of the third group (III), we used the following parameters: the crystal growth rate was$V=6mm/min$ , the axial temperature gradient was$G=130K/сm$ , the oxygen concentration was$N\left(0\right)={10}^{18}c{m}^{-3}$ , and the carbon concentration was$N\left(0\right)={10}^{18}c{m}^{-3}$ . Group III correspond to the conditions for growth of small–sized silicon single crystals with the use of crucibleless floating zone melting (Table 1).

In this the computing experiment, assumed that the concentration of nucleation centers for complexes constitute$~{10}^{12} c{m}^{-3}$ . This value corresponds to the experimental data obtained by transmission electron microscopy.⁴ The densities of distribution of complexes of silicon–carbon for crystals I and II groups are shown in Figure 1. The densities of distribution of complexes of silicon–carbon for crystals III are shown in Figure 2.

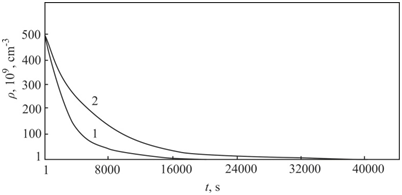
Figure 1 Changing the density of distribution of complexes silicon–carbon for crystals I (1) and II(2) groups.

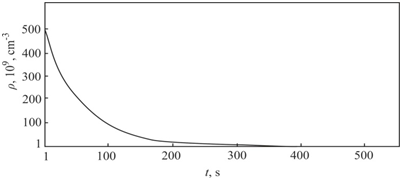
Figure 2 Changing the density of distribution of complexes silicon–carbon for crystals III group.

The precipitation process begins near the crystallization front. The results of the calculations performed in groups I, II and III allow us to compare the processes of precipitation in the CZ–Si and FZ–Si crystals and to analyze them for almost maximum contents of the oxygen and carbon impurities. Changing crystal growth rate or axial temperature gradient as results reduced time of the nucleation stage. Furthermore, the calculations in group III showed that this changing leads to decrease of precipitates average radius in FZ–Si crystals as compared to the CZ–Si crystals at the stage of the growth of precipitates.

The simultaneous nucleation and growth of particles of the new phase (oxygen and carbon precipitates) during cooling of as–grown silicon crystals leads to a strong interplay between the processes of evolution of these two subsystems of grown–in micro defects. The absorption of vacancies by oxygen precipitates results in the emission of silicon atoms in interstitials. The silicon atoms interact with carbon precipitates, which supply vacancies for oxygen precipitates. This interplay between the processes leads to an accelerated changeover of the subsystems of oxygen and carbon precipitates to the stage of the coalescence as compared to the independent evolution of these two subsystems.¹³

The condition providing changeover to the stage of the coalescence is written in the form$R\left(t\right)\approx R_{cr}\left(t\right)$ , which is satisfied at the temperature$T\approx 1423K$ . The stage of the coalescence in large–scale crystals begins at temperatures close to the temperatures of the formation of intrinsic point defects clusters (microvoids or interstitial dislocation loops).¹³ Figure 3 shows the variation of the average size of oxygen and carbon precipitates at the stage of the coalescence in the temperature range of cooling from 1423 to 300 K.

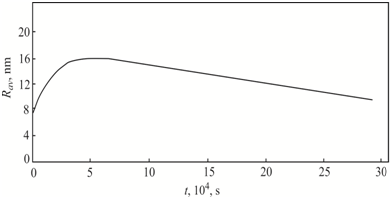
Figure 3 Variation of the average size R_av of (1) oxygen precipitates at the stage of the coalescence during cooling of the CZ–Si crystals in the temperature range from 1423 to 300 K.

Although the concentrations of oxygen and carbon in crystals of groups I, II and III are identical, the change in the thermal conditions for the growth of small–sized FZ–Si single crystals (high growth rates and axial temperature gradients) leads to the fact that the stage of the coalescence begins far in advance (at$T\approx T_m-20K$ ). In the classical theory of the formation of second–phase particles during heat treatments of single crystals, the formation of critical nuclei of small sizes occurs at low temperatures. In the classical theory of the formation of second–phase particles during heat treatments of single crystals, the formation of critical nuclei of small sizes occurs at low temperatures. Here an increase in the temperature leads to the growth and coalescence of precipitates. In real crystals, already there are grown–in micro defects. These micro defects during thermal treatments are sinks for intrinsic point defects and impurities. Using of Vlasov's model for solids to the complication processes during crystals thermal treatment gives another result (Figure 4).

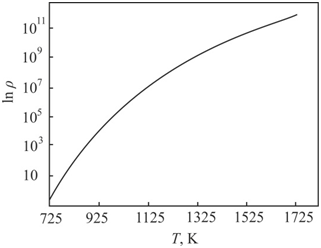
Figure 4 Dependence of the density of distribution for the silicon–oxygen complexes from the temperature during the annealing of the crystal.

In accordance with Vlasov's model for solids the complexation at$T\approx 723K$ is unlikely. This temperature corresponds to the formation of thermal donors. The complexation in silicon during thermal treatment is possible only at high temperatures. Excess intrinsic point defects and impurities disappear at initial structural defects. This process leads to transformation of initial defect structure of crystal.

At the same time, it is known that the thermal treatments of silicon lead to the formation of electrically active centers. If the formation of complexes in the temperature range$300K\le T\le 600K$ is unlikely then the processes of coalescence occur in crystals of any diameter. Then, can be assumed that the dissolving grown–in precipitates lead to formation of electrically active centers.

We note that classical theory of nucleation and growth of second–phase particles and Vlasov's model for solids lead to identical results. Both approaches describe the processes of high–temperature precipitation of impurities. In turn, the high–temperature precipitation of impurities is the basis of the process of defect formation in crystals.

Until now the probabilistic approach (Vlasov's model for solids) for real crystals has not been applied. At the same time joint use of both approaches would allow for a fresh look at known facts and discover new phenomena and laws. This work represents the first attempts in the last 70 years to obtain the solution of Vlasov model for solid state. Questions of application of the Vlasov model for solid state for description of the nucleation of defect structure, taking into account of the thermal conditions of the crystal growth were discussed. There are the following main results:

1. The concepts and principles of Vlasov physics are fully applicable to solid state.
2. The Vlasov model for solid state describes the processes of complexation during the growth of real crystals adequately classical theory of nucleation and growth of second–phase particles in solids.
3. Method of calculation of the initial defect structure of crystals was proposed.
4. Using Vlasov’s model for solids shown that during of low–temperature crystal treatments proceeds the processes of coalescence of grown–in defects.

None.

Author declares there is no conflict of interest.

1. Born M, Huang K. Dynamical theory of crystal lattices. UK: Clarendon Press; 1954.
2. Cristian JW. The theory of transformations in metals and alloys. UK: Pergamon Press; 1965.
3. Talanin VI, Talanin IE. Diffusion model of the formation of growth microdefects: A new approach to defect formation in crystals (Review). Physics of the Solid State. 2016;58(3):427–437.
4. Talanin VI, Talanin IE. Formation of grown–in microdefects in dislocation–free silicon monocrystals. In: Elliot TB, editor. New Research on Semiconductors. USA: Nova Science Publishers; 2006.
5. Talanin VI, Talanin IE. Kinetics of high–temperature precipitation in dislocation–free silicon single crystals. Physics of the Solid State. 2010;52(10):2063–2069.
6. Vlasov AA. Journal of Physics.1945;9:130.
7. Vlasov AA. Nonlocal Statistical mechanics. Russia: Nauka; 1978.
8. Kozlov VV. The generalized Vlasov kinetic equation. Russian Mathematical Surveys. 2008;63(4):691–726.
9. Vlasov AA. Many–particle theory and its application to plasma. USA: Gordon & Breach Science Publishers; 1961.
10. Talanin VI, Talanin IE. Complex formation in semiconductor silicon within the framework of the Vlasov model of a solid state. Physics of the Solid State. 2016;58(10):2050–2054.
11. Vedenyapin VV. Boltzmann and Vlasov kinetic equations. Russia: Fizmatlit; 2001.
12. Lifshitz EM, Pitaevskii LP. Physical Kinetics. UK: Pergamon Press; 1981.
13. Talanin VI, Talanin IE. Kinetic model of growth and coalescence of oxygen and carbon precipitates during cooling of As–grown silicon crystals. Physics of the Solid State. 2011;53(1):119–126.
14. Slezov VV, Sagalovich VV. Usp Fiz Nauk. 1987;151:67.
15. Vanhellemont J. Diffusion limited oxygen precipitation in silicon: Precipitate growth kinetics and phase formation. Journal of Applied Physics. 1995;78(6).