We study the consequences of defining the Debye region in astrophysical plasmas as that region where purely stochastic Poissonian density fluctuations must be perturbed by the appearance of unscreened electric Coulomb forces. Here by we test a new definition of the charge screening length requiring that purely statistical density fluctuations in sub-volumes of the system can only be expected, if particle residence probabilities in those volumes are uncorrelated. We find that within Debye spheres where electric micro fields appear, this can evidently not anymore be guaranteed. We introduce a new definition of the charge-screening length based on this requirement. It turns out that the newly defined charge screening length increases compared to its classical Debye value proportional to the so-called Debye number, i.e. the number of particles in the Debye sphere, while the classical Debye length delivers one unique result independent on the Debye number. We discuss the astrophysical relevance of this new definition which has the consequence that the effective screening length increases with the square of the temperature and decreases inversely proportional to the density, instead of with their square roots as in classic representations. Based on this revised Debye concept we furthermore study the general dispersion relation for electrostatic waves and show, that these waves when propagating into the direction of increasing electron temperatures will grow nonlinear and thus dissipate their excess energy to the electrons, with the consequence of heating them further up. This naturally explains the occurence of observed electron temperature increases at space plasma passages over MHD shocks. Furthermore we study the radiowave scattering in a plasma environment due to density-fluctuations which induce dielectricity fluctuations exciting secondary dipolar radio waves which latter serve as a valuable diagnostic tool for plasma investigations.

Keywords: debye region, astrophysical plasmas, Coulomb forces, radiowave scattering, dielectricity fluctuations

Ensembles of large-numbers of particles, microscopically considered, do not have a unique homogeneous particle density $n= {\langle n\left(l\right)\rangle }_l$  independent on spatial scales l. In contrast, the smaller are the spatial scales l under consideration, the more pronounced is the expectation value of the occurring density fluctuation $\delta n\left(l\right),$  even though the density average over sufficiently large time periodsnevertheless is given by the expectation value $n= {\langle n\left(l\right)\rangle }_t= \left(1/\tau \right){\displaystyle {\int }_0^{\tau }n\left(l,t\right)dt}.$ This evidently also allows to conclude that the differential phase-space density $\delta n\left(r,v\right)=f\left(r,v\right)d^{3}v{d}^{3}r$ is a fluctuating quantity, especially in the weakly populated wings of the distribution function $f\left(r,v\right),$ where this function attains the smallest values, there relative fluctuations become important. This means that comparing to the bulk densities the wing densities are showing higher relative fluctuation amplitudes. The stochastic expression for these probabilistically expectable density fluctuations can be worked out with the theory of Poissonian statistics^1–3 which latter, however, is developed under the Boltzmann´ìan assumption that the distribution of particles in space is completely uncorrelated, meaning that the presence of a particle in a sub volume $\Delta V$ is completely uncorrelated with the probability to have other particles of different velocities in the same space volume at the same time. This can of course only then be considered as a reasonable assumption, if all particles, due to the exclusive existence of short-range forces (e.g. like hard-core atomic forces, polarization forces or Van der Waals forces), over the dimension $\Delta V$ effectively can be considered as non-interacting particles, - particles which - so to speak - do not "know" of their mutual, respective presence, i.e. they do not recognize each other. As soon, however, as long-range forces, e.g. like Coulomb forces or gravitational forces, are involved into the game on a dimension of $\sqrt[3]{\Delta V},$ the residence probability of a particle in that sub-volume $\Delta V$ is not anymore uncorrelated with the presence of other particles there.

Usually in form of space plasmas one generally has in view a quasi-neutral mixture with identical densities of negatively and positively charged particles (i.e. electrons and protons in most cases). Since the densities of electrons and protons on small scales are fluctuating, one has to expect uncorrelated electric field fluctuations. Under equilibrium conditions no large-scale electric fields are maintained in such quasi-neutral environments, however, on small scales of the order of Debye lengths ${\lambda }_D$ or smaller,⁴ i.e. for $l\le {\lambda }_D,$  electric micro-fields evidently are present due to the manifestation of unshielded single electric charges in these subregions.^5–7 Since in these small scale regions no quasi-neutrality, i.e.$n_i\simeq {ñ}_e,$ can be assumed, for wavelengths $\lambda \le {\lambda }_D$  the dispersion relation for electrostatic waves differs substantially from the commonly used one and attains a more complicated form^8,9 given by:

$\omega =k\sqrt{\frac{K{T}_e}{M}\frac{1}{1+{\left(k{\lambda }_D\right)}^2}+\frac{K{T}_i}{M}}$

With $\omega$ and k denoting the wave frequency and the wave vector, with $T_i$ and $T_e$ being the ion and electron temperature, respectively, and M, denoting the ion mass. This interestingly enough shows that for wavelengths $\lambda \le {\lambda }_D$ electrostatic waves enter into a very specific propagation mode which commonly is not properly recognized.¹⁰ In this article here we now want to look at these aspects from a different view, namely turning the above question to the inverse, - rather asking now - what region should be defined as Debye region, if it is just in this region that unshielded electric fields do compete with stochastic density or pressure force fluctuations, in other words defining the Debye region by that characteristic scale $\lambda ={\lambda }_{PD}$ where Poissonian density fluctuations are perturbed due to field-correlated residence probabilities of the particles.

Let us first consider here the stochastic residence probabilities to find a sub number $\Delta n$  of particles in a sub volume $\Delta V$ of the system. The specific probability to have μ particles in a volume $V=V_0+\Delta V,$ where $V_0$ is the norm-volume of these μ particles given by the relation:$\mu /V_0=N/V=n,$ is given by:¹¹

$W\left(v\right)=W_0\exp [-\frac{\mu }{2}{(\frac{\Delta V}{V_0})}^2]$

In addition it can be well concluded for the Debye sphere, that the probability to have $N_D$ particles in a volume $V=V_D+\Delta V_D,$  where $V_D$  is the Debye norm-volume of $N_D$ particles (the so-called Debye number $N_D=n{V}_D=n\left(4\pi /3\right){\lambda }_D^3$ related to:$N_D/V_D=N/V=n),$  thus is given by

$W\left(N_D\right)=W_0\exp [-\frac{N_D}{2}{(\frac{\Delta V_D}{V_D})}^2]$

where the probability weight $W_0=W(\Delta V_D=0)$ is taken to be equal to 1! The above relation then leads to

$W\left(N_D\right)=\exp [-\frac{n{V}_D}{2}{(\frac{\Delta V_D}{V_D})}^2]=exp[-\frac{n}{2}\frac{\Delta V_D^2}{D}]$

With the probability $W\left(\Delta V_D\right)$ that $\Delta V_D$ is the volume fluctuation of $N_D$ ions, one can calculate the most probable fluctuation volume $\Delta {\overline{V}}_D$ as:

$\Delta {\overline{V}}_D=\varsigma {\displaystyle \int \Delta V_D}W\left(\Delta V_D\right)d\Delta V_D=\varsigma {\displaystyle {\int }_0^{\infty }\Delta V_D}\exp [-\frac{n}{2}\frac{\Delta V_D^2}{V_D}]d\Delta V_D=\varsigma V_D^2{\displaystyle {\int }_0^{\infty }X\exp [-\frac{N_D}{2}{X}^2}]dX$

Where $\varsigma$ takes care of normalizing the probability function $W(\Delta V_D)$ and hence is calculated to

$\varsigma =\frac{1}{V_D}\sqrt{\frac{2N_D}{\pi }}$

Be

which then yields the most-probable fluctuation volume as

$\Delta {\overline{V}}_D=\varsigma V_D^2{\displaystyle {\int }_0^{\infty }X\exp [-}\frac{N_D}{2}{X}^2]dX=\varsigma V_D^2\frac{\Gamma \left(1\right)}{N_D}=\sqrt{\frac{2N_D}{\pi }}{V}_D\frac{\Gamma \left(1\right)}{N_D}$

Where $\Gamma \left(x\right)$ is the well known Gamma function. This, with $\Gamma \left(x\right)=1,$ finally delivers

$\Delta {\overline{V}}_D=V_D\sqrt{\frac{2}{\pi N_D}}$

With this above result for the most probable volume fluctuation one obtains, - assuming that volume and temperature fluctuations are uncorrelated -, and - for the moment here - that electron and ion temperatures are identical - , the associated Poissonian pressure fluctuations which then are given by

$\delta {\overline{P}}_D=P-\overline{P}=KT\delta \overline{n}=-KTn\left(\Delta {\overline{V}}_D/V_D\right)=-KT·n\sqrt{\frac{2}{\pi N_D}}$

Within the Debye sphere this leads to a pressure force per particle of ${\Pi }_D=-\nabla \delta {\overline{P}}_D/n$ given by

${\Pi }_D=(\frac{\delta {\overline{P}}_D}{{\lambda }_D}\frac{1}{n})=-\frac{1}{{\lambda }_D}KT\sqrt{\frac{2}{\pi N_D}}$

Now we have to respect that within the Debye sphere the Poissonian fluctuation pattern is perturbed due to competing electric Coulomb forces of unscreened electric charges. Hence we expect that just within this sphere, where the Poissonian pressure fluctuation force ${\Pi }_D$ competes with the single-charge electric field force ${\in }_D=e{E}_D$ of an unscreened charge e the normal Poissonian pressure fluctuation pattern is perturbed. This means we now and here consider the "effective Debye sphere" as to be that specific region with non-Poissonian pressure fluctuations, defined by the following criterion:$\left|{\Pi }_D\right|=\left|{\in }_D\right|$   and thus consequently we obtain the following relation for the so-called "Poissonian Debye length" ${\lambda }_{PD}:$

$\frac{e^2}{{\lambda }_{PD}^2}=\frac{1}{{\lambda }_{PD}}KT\sqrt{\frac{2}{\pi N_D}}$

which then further on leads to:

${(\frac{e^2}{KT})}^2=\frac{3}{2{\pi }^{2}n{\lambda }_{PD}}$

or finally to:

${\lambda }_{PD}=\frac{3{(KT)}^2}{2{\pi }^{2}n{e}^4}={\lambda }_{D0}· ({\lambda }_{D0}^{3}n)=\frac{3}{4\pi }{\lambda }_{D0}{N}_{D0}$

where in the above relation the classical Debye length has been introduced with ${\lambda }_{P0}=\sqrt{KT/(4\pi n{e}^2)}.$ This above formulation expresses the fact that the Poissonian Debye length ${\lambda }_{DP}$ is larger or smaller than the classical Debye length ${\lambda }_{D0}$ dependent on, whether the classical Debye number $N_{D0}$ is larger or smaller than$(4\pi /3).$   This for the first time also now opens the opportunity to even obtain a value for PD for the condition that the number of particles in the Debye region is not a statistically relevant one, which in fact does not allow to at all consider the charge screening on a statistical basis.

While the classical Debye length shrinks as function of the density according to $(1/\sqrt{n}),$  and increases as function of the temperature according to $\sqrt{T},$  the above derived Poissonian Debye length ${\lambda }_{DP}$ reacts to these quantities by

${\lambda }_{PD}={\lambda }_{D0}·N_{D0}\approx (\sqrt{\frac{T}{n}}(\frac{T^{3/2}}{n^{1/2}})\approx \frac{~T^2}{n}$

i.e., compared to the classical Debye length ${\lambda }_{D0},$ it thus decreases more strongly with the increase of the density, namely by $(1/n),$ and also increases more strongly with temperature, namely by $T^2.$

We can also look here at the ratio $R_{P,D}={\lambda }_{PD}/{\lambda }_{D0}$ of the Poissonian over the classical Debye length and obtain for this ratio

$R_{P,D}={\lambda }_{PD}/{\lambda }_{D0}=n(\frac{4\pi }{3}){[\frac{KT}{4\pi n{e}^2}]}^{3/2}=\frac{4}{3}\pi · {6.9}^3\left|\frac{{\overline{T}}^{3/2}}{{\overline{n}}^{1/2}}\right|= 1376\left|\frac{{\overline{T}}^{3/2}}{{\overline{n}}^{1/2}}\right|=\frac{3}{4\pi }1376 · N_{D0}=328 · N_{D0}$

Where $\overline{T}$ must be measured in Kelvin and $\overline{n}$ in $c{m}^{-3}.$ This means that for a Debye number $N_{D0},$ which falls off  with density like $1/\sqrt{n,}$ of $N_{D0}=1/328,$    i.e. just for the case of statistical irrelevance, the two Debye lengths would become equal.

It is well known that fluctuating dielectrica induce scatterings of electromagnetic wave power by causing secondary waves, e.g. Rayleigh scattering, aerosole scattering, or the blue-sky phenomenon. This is connected with the fact that propagating electromagnetic waves under fluctuating environmental dielectricity conditions $\delta \epsilon (l,E(t))=\epsilon (r,t)-{\overline{\epsilon }}_l$ on scales l induce time-dependent local electric dipoles which by themselves radiate frequency-coherent secondary waves, i.e. scatter the original wave by parts. This means the propagation of electromagnetic radiowaves in a plasma environment, due to the coherent dielectricity fluctuations excites as well radiowave scatterings. If the scale of the fluctuation volume $l=\sqrt[3]{\Delta V}$ is small compared to the wavelength $\lambda$  of the radiowave, then it can be assumed that the wave locally induces a homogeneous, dipole-inducing electric field extended over the volume $\Delta V$  which would allow to apply Poissonian statistics, as long as the number of particles in this fluctuation volume, i.e. $n\Delta V$  is a statistically significant or relevant number. Hence, assuming $\lambda \simeq 1m$  and $l\simeq 10cm$  then, with an electron density of $n=1c{m}^{-3}$  this would yield a statistically relevant number of about 10³ particles in the fluctuation volume, i.e. would permit to apply statistical considerations as carried out in section 2 of this paper. First we can calculate here the electric dipole moment of the volume $\Delta V$  and obtain

$\overrightarrow{\mu }={\epsilon }_0\langle \epsilon (r,t)-{\overline{\epsilon }\rangle }_l\Delta V\cdot \overrightarrow{E}={\epsilon }_0\Delta {\epsilon }_l\Delta V\cdot \overrightarrow{E}$

Consequently connected with the time-dependent electric field $\overrightarrow{E}=\overrightarrow{E}(r,t)$ a co-herently time-dependent electric dipole $\vec{\mu }=\vec{\mu }(r,t)$ is induced which by itself emits in its typical dipolar characteristics, like a dipolar antenna does as well, i.e. a secondary wave with a dipolar emission characteristic originates. At a distance $r\gg d$  (radiation zone!) one then obtains the following emission intensity (see e.g. Weizel, 1973b)

$S(r,\theta )=\frac{{\pi }^{2}c{\mu }^2}{2{\epsilon }_0{\lambda }^4{r}^2}si{n}^2\theta =\frac{{\pi }^{2}c\Delta {\epsilon }^2\Delta V^2{E}^2}{2{\epsilon }_0{\lambda }^4{r}^2}si{n}^2\theta$

Where $\theta$  is the angle between the infalling and the scattered wave. The above expression can be written in the following form, then containing the intensity of the primary wave $S_0=(1/2)(\overrightarrow{D}\cdot \overrightarrow{E})=(1/2)\overrightarrow{\epsilon }{\epsilon }_0{E}^2$ when given in the form

$S(r,\theta )=S_0\frac{{\pi }^{2}c\Delta {\epsilon }^2\Delta V^2}{{\epsilon }_0^2{\lambda }^4{r}^2}si{n}^2\theta$

Now we can make use of the density-dependence of the dielectricity in the form

$\frac{\Delta \epsilon }{\epsilon }=\frac{1}{\epsilon }\frac{d\epsilon }{d\rho }\Delta \rho =\frac{\rho }{\epsilon }\frac{d\epsilon }{d\rho }\delta$

where the density fluctuation $\delta$  has been defined by $\delta =\Delta \rho /\rho$  Calculating next the statistical mean of $\delta$  by using the expression developed in section 2 (Equ. 12), one finds

$\langle {\delta }^2\rangle =\frac{{\displaystyle \int {\delta }^2\exp [-v\frac{{\delta }^2}{2}]d\delta }}{{\displaystyle \int \exp [-v\frac{{\delta }^2}{2}]d\delta }}=\frac{1}{v}$

where $\nu =n\Delta V$  is the expectation number of electrons in the volume $\Delta V$  then one obtains the intensity of scattered radiation in the form

$S(r,\theta )=S_0\frac{\Delta V}{n}\frac{{\pi }^2{\rho }^2{(\frac{d\epsilon }{d\rho })}^2}{{\epsilon }_0^2{\lambda }^4{r}^2}si{n}^2\theta$

The change $d\epsilon /d\rho =(1/M)d\in /dn$  of the dielectricty $\epsilon$  with changing density n hereby can be derived with the help of the well-known Lorentzian formula of the optics.

The Poissonian average of the density fluctuation $\delta \overline{n}$ over a Debye volume as derived in Equ. (12) of section 2 is given by

$\delta \overline{n}=-n\sqrt{\frac{2}{\pi N_D}}$

and consequently one can express the scattered radiation flux by

$S(r,\theta )=S_0\frac{\Delta V}{n}\frac{{\pi }^2{n}^2\delta {\overline{n}}^2{(\frac{d\epsilon }{dn})}^2}{{\epsilon }_0^2{\lambda }^4{r}^2}si{n}^2\theta =S_0\Delta V\frac{1}{N_D}\frac{2\pi n^3{(\frac{d\epsilon }{dn})}^2}{{\epsilon }_0^2{\lambda }^4{r}^2}si{n}^2\theta$

As becomes evident from the above expression, the relative intensity $S/S_0$ of the scattered radiation depends on the Debye number $N_D$ being inversely proportional to it. The dependence on the effective (Poissonian) Debye length ${\lambda }_{PD}$ can even better be expressed by rewriting the above expression in the following form:

$S(r,\theta )=S_0\Delta V\frac{\frac{3}{2}n{\lambda }_{PD}{(\frac{d\epsilon }{dn})}^2}{{\epsilon }_0^2{(\lambda /{\lambda }_{PD})}^4{r}^2}si{n}^2\theta$

Our conclusion thus is that by studying the spectral behaviour of the scattered intensity of radiowaves with wavelengths $\lambda \gg {\lambda }_D$ propagating through a plasma environment with an electron density n one should be able to find indications for the actual value of the effective Debye length ${\lambda }_{PD}$ and also the actual Debye number $N_D$ .

As already mentioned earlier in this paper the generalized dispersion relation for electrostatic electron plasma waves, when replacing ${\lambda }_D$  by ${\lambda }_{PD}$  as setting the limit of validity of the plasma approximation, i.e. $n=n_e=n_i$ , is given by:⁴

$\omega =k\sqrt{\frac{K{T}_e}{M}\frac{1}{1+{(k{\lambda }_{PD})}^2}+\frac{K{T}_i}{M}}$

Introducing first now the electron plasma frequency ${\omega }_{pe}=\sqrt{4\pi n{e}^2/m}$ , the classical Debye length ${\lambda }_{D0}=\sqrt{K{T}_e/4\pi n{e}^2}$ , the Debye wave vector $k_{D0}=2\pi /{\lambda }_{D0},$ and the definition of the effective Poissonian Debye length ${\lambda }_{PD}=R_{PD}\cdot {\lambda }_{D0}$ , with $R_{PD}126T^{3/2}/n^{1/2}$  we then find:

$\omega /{\omega }_{pe}=k\sqrt{\frac{m}{4\pi n{e}^2}\frac{K{T}_e}{M}(\frac{1}{1+{(k{\lambda }_{P,D})}^2}+\frac{T_i}{T_e})}$

and furthermore

$\omega /{\omega }_{pe}=2\pi (k/k_{D0})\sqrt{\frac{m}{M}(\frac{1}{1+(2\pi R_{PD}{(k/k_{D0})}^2}+\frac{T_i}{T_e})}$

When introducing now normalized quantities with $\overline{\omega }=\omega /{\omega }_{pe}$  and $\overline{k}=k/k_{D0}$  one finds

$\overline{\omega }=2\pi \sqrt{\frac{m}{M}}\overline{k}\sqrt{\frac{1}{1+{(2\pi R_{PD}\overline{k})}^2}+\frac{T_i}{T_e}}$

and finally denoting $\overline{\Omega }=\omega /{\omega }_{pi}=\omega /{\omega }_{pe}\sqrt{M/m}$  one can write 

$\overline{\Omega }=2\pi \overline{k}\sqrt{\frac{1}{1+{(2\pi R_{PD}\overline{k})}^2}+\frac{T_i}{T_e}}$

The above dispersion relation is displayed in Figure 1 and shows that always there exists a part of the relation connected with a vanishing or nearly vanishing group velocity with $v_g({\omega }_s)={\left|\partial \omega /\partial k\right|}_{{\omega }_s}\simeq 0$ . It turns out that this ”standing wave”- branch occurs at the higher frequencies ${\omega }_s$ , the higher is the effective Debye length ${\lambda }_{P,D}=R_{PD}\cdot {\lambda }_{D0}$ , or, so to say it in other words, the electron temperature $T_e$ . This for instance means that electrostatic turbulent waves at subcritical frequencies $\omega \le {\omega }_s$  when propagating into regions with increasing electron temperatures $T_e$ , then may naturally enter a region in which their frequencies $\omega$  become equal to the local value of ${\omega }_s$ . This furtheron then, however, implies that the group velocity $v_g(\omega \simeq {\omega }_s)$  by which turbulent wave energy is transported slows substantially down there, and turbulent fluctuation amplitudes consequently have to grow to keep the turbulent wave energy flow constant.^12–14 Thus it can happen that in such regions of slowly increasing temperatures the pile-up of turbulent electrostatic energy leads to an amplitude growth from the linear to the nonlinear wave regime. As soon as electrostatic waves, however, grow to nonlinear amplitudes, they then start dissipating their wave energy to thermal degrees of freedom of the electrons (i.e. dissipation of wave energy into electron thermal energy), and thus will induce an additional electron heating, i.e. will drive the electron temperatures even higher in this region.

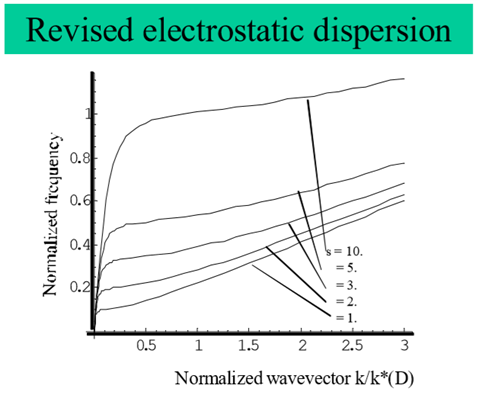
Figure 1 Shown is the electrostatic dispersion relation $\omega =\omega (k)$ showing the normalized frequency $\omega /{\Omega }_i$ on the ordinate as function of the normalized wavevector $k/k_D$ on the abscissa. The parameter s is equal to the number $R_{PD}$ introduced in the text.

This form of electrostatic wave energy dissipation could perhaps be the reason why at shocks - like e.g. especially the solar wind termination shock - ions must be expected to behave differently from electrons what concerns their polytropic reactions to the downstream density increases, concerning their shock-induced specific temperature increases.^15–18 Normally the Rankine-Hugoniot relations do consider electrons and ions as thermally reacting in identical forms. But even in case both species, according to the conventional Rankine-Hugoniot relations, were expected to first react according to identical polytropic relations, the electrons downstream of the shock might additionally be heated up via wave energy dissipation according dissipation of steepened electrostatic waves allong the aforementioned argument. This means that they are nevertheless then furtheron differentially heated up with respect to protons due to being additionally heated by the energy dissipation of the nonlinear electrostatic waves which are convected into the downstream region selectively heating electrons. (see illustration given in our).This could be an alternative or additional explanation for the strong electron heating predicted in papers like Chalov et al.^15–18 Most recently there was even given a proof connected with Voyager-2 data  that KeV-energetic electrons are produced at the passage of solar wind electrons over the solar wind termination shock.¹⁹

In order to quantitatively check the efficiency of this latter heating process one should first of all know more about the wave amplitudes of the electrostatic noise level upstream of the termination shock, in order to judge the energy that is available for dissipation to electrons. Furthermore one also should be able to make sure that the wave-electron coupling periods are short enough to allow for the wave-induced heating of the electrons while passing over the shock structure. For the latter the so-called Landau damping periods may give a characteristic measure.^8–10 Evaluated at the point of maximum growth one might find growth periods of  Kadomtsev et al.^20–22

${\tau }_L=\frac{1}{{\gamma }_{\max }}\approx \frac{1}{{\omega }_{pe}}\frac{2}{\sqrt{3}}\sqrt[3]{\frac{4M}{m}}.$

with ${\omega }_{pe}$ denoting the local electron plasma frequency and M and m being the masses of ions and electrons, respectively. This expression at the location of the solar wind termination shock evaluates to ${\tau }_L\approx {10}^{-2}\sec$  which just is in the order of the electron passage time over the shock ${\tau }_t\approx 10{\lambda }_D/U\approx 8\cdot {10}^{-3}\sec$  and thus means that the wave-electron coupling during the shock passage is well possible. Similar results were also found earlier by Chashei et al.²³ on the basis of studying the Buneman instability based on the counterstreaming of electrons and protons at the shock.^24,25

In this article we have considered stochastic density fluctuations in astrophysical plasmas and have emphasized the important point that such fluctuations can only then be described by means of Poissonian statistics, if the particle residence times within the volumes of such density fluctuations are uncorrelated. This, however, cannot be expected being the case, if for instance electrical forces connected with unscreened electrical charges enforce the correlation of particle residence times. In order to define the Poissonian limit of permitted volumes of density fluctuations we compare forces due to pressure fluctuation forces with electric forces in these volumes due to uncreened electric charges. Following this idea we can define the so-called Poissonian Debye length which contains as a factor the classical Debye length⁴ and the number of particles in the Debye sphere, the so-called Debye number. It turns out that this modification of the Debye length clearly expresses the statistical relevance of the number of charge-screening particles. This result has a broad astrophysical meaning as we demonstrate. On the basis of this newly defined "effective" Debye length we study the dispersion relation of electrostatic waves in astrophysical plasmas and do show that electrostatic waves with a specific frequency $\omega$  when propagating into plasma regions with increasing electron temperature where the group velocity $d\omega /dk$  of this wave becomes small or even vanishes (i.e. standing waves !, see Figure 1), then turbulent wave energy has to be dissipated and electron temperatures are even more increased there. This means that the wave amplitudes of such waves grow nonlinear and the waves start dissipating wave energyinto kinetic, i.e.thermal energy. By this mechanism electrostatic waves in regions of increasing electron temperatures do contribute to an additional heating of electrons. Especially at astrophysical MHD shocks¹⁷ this may help to strongly and selectively heat electrons compared to protons at their passage over the shock to the downstream region.

We furthermore discuss observational possibilities to measure the Poissonian Debye length in astrophysical plasmas by transmission of a radiowave through these plasmas observing the extinction of the wave intensity due to excitation of locally generated, secondary dipolar waves. When the radiowave length is larger than the local Poissonian Debye length, then the local excitation of secondary waves occurs and modifies the radiowave intensity of the penetrating wave, while at wavelengths shorter than the local Poissonian Debye length coherent secondary waves will not be excited.

None.

The author declares there is no conflict f interest.

1. Joos G. Lehrbuch der Theoretischen Physik. 10. Auflage, Geest & Portig K.G., Leipzig. 1959. p. 539–554.
2. Weizel W. Lehrbuch der Theoretischen Physik. Zweiter Band (2.Auflage), Springer Verlag, Heidelberg. 1973A. p. 1480–1485.
3. Landau LD, Lifshitz EM. Statistical Physics, Part 1 (3rd Edition, Course of Theoretical Physics, Volume 5). New York 1998.
4. Chen FF. Introduction to plasma physics. 1974, New York, Plenum Press Debye, Phys. Z. 1920. p. 21–181.
5. Hunger K, Larenz RW. Das Mikrofeld im Plasma. Zeitschr f Physik. 1961;163:245–261.
6. Ichimaru S. Basic Principles of Plasma Physics: A statistical approach. Benjamin Publ., New York, 1973.
7. Spatschek KH. Theoretische Plasmaphysik. Teubner Studienbücher, Physik, B.G.Teubner, Stuttgart, 1990.
8. Baumjohann W, Treumann RA. Basic space plasma physics. London Imperial College Press. 1996.
9. Goedbloe H, Poedts S. Principles of Magnetohydrodynamics. Cambridge University Press, Cambridge (UK). 2004.
10. Fahr HJ, Richardson JD, Verscharen D. Probing the thermodynamic conditions of the heliosheath plasma by shock wave propagation. Astron & Astropyhs. 2015;579:A18.
11. Weizel W. Lehrbuch der Theoretischen Physik. Erster Band (2.Auflage), Springer Verlag, Heidelberg. 1973B. p. 480–485.
12. Scudder JD. On the causes of temperature changes in inhomogeneous low-density astrophysical plasmas. Astrophys J. 1992;389:299.
13. Schwartz SJ, Thomsen MF, Bame SJ, et al. Electron heating and the potential jump across fast mode shocks. J Geophys Res. 1988;93:12923.
14. Leubner MP. Wave induced suprathermal tail generation of electron velocity space distributions. Plan Space Sci. 2000;48:133.
15. Chalov SV, Fahr HJ. On the effect of transport coefficient anisotropy on the plasma flow in heliospheric interface. MNRAS. 2013;433:L40–L45.
16. Fahr HJ, Siewert M, Chashei IV. On the electron temperature downstream of the solar wind termination shock. Astrophys Space Sci.  2012;341:265–276.
17. Fahr HJ, Siewert M. Probing the thermodynamic conditions of the heliosheath plasma by shock wave propagation. Astron & Astrophys. 2013;558:A41.
18. Fahr HJ, Verscharen D. The behavior of electrons at the heliospheric shock transition. Astron & Astrophys. 2016;587:L1.
19. Fahr HJ, Krimigis SM, Fichtner H, et al. The behavior of electrons at the heliospheric shock transition. Astrophys J Lett. 2017;848:L3.
20. Kadomtsev BB. Plasma turbulence. Academic Press, New York, 1965.
21. Sagdeev RZ, Galeev AA. Nonlinear Plasma Theory. In: D.O ‘Neill, T. Benjamin et al. editors. Book, New York, 1969.
22. Papadopoulos K. A review of anomalous resistivity for the ionosphere. Rev Geophys Space Physics. 201977;15:113.
23. Chapman S, Cowling TG. Mathematical Theory of Non-Uniform Gases. Cambridge University Press, Cambridge 1961.
24. Chashei IV, Fahr HJ. On the electron temperature downstream of the solar wind termination shock. Ann Geophys. 2013;31:1205–1212.
25. Fahr HJ, Heyl M. Quasi-thermal noise spectroscopy: The art and thepractice. Astron & Astrophys. 2016;589:A85.