The Coleman-Weinberg Potential has and is still being applied in so many areas in modern physics which include analysis of Spontaneous Symmetry Breaking (SSB). In the SM, SSB is attained by introducing an ad-hoc kind of modification resulting in the mass term of the of the classical potential assuming a tachyon-like characteristics. By analyzing all the terms in the classical potential, it is vivid that only the mass term possesses a dimensional constant. Thus, we can trace the Hierarchy Problem to the ad-hoc modification via the squired mass term. This paper does not only focus on the study of the Coleman-Weinberg mechanism but also shows why application of the same is likely to unveil a clue that may lead scholars to resolving the Hierarchy Problem.

Keywords: Coleman-Weinberg Potential, Hierarchy Problem, Spontaneous Symmetry Breaking

In view of the SM, the Higgs mechanism has been proved to be the one responsible for originating masses for fermions and gauge bosons. Without this mechanism, gauge symmetry in the SM, which does not permit mass generation, would have left fermions and bosons massless.¹ Such a scenario contradicts the Large Hadron Collider (LDC) accelerator facility’s measurements. In addition, one of the recipe for the Higgs mechanism, in line with experimental results, is an acquisition of a non-zero vacuum expectation value resulting in triggering SSB. Fermions and bosons’ interaction with the scalar field $\varphi$ at the vacuum expectation value generates their masses. This entails that the ${\varphi }^4$ theory with reference to a real scalar field serves as a classical example to study SSB in the SM.

To begin with, this theory is governed by the Lagrangian density

$ℒ=\frac{1}{2}{\partial }_{\mu }\varphi {\partial }^{\mu }\varphi +V\left(\varphi \right)$   (1)

where

$V\left(\varphi \right)=\frac{1}{2}{m}^2{\varphi }^2+\frac{\lambda }{4!}{\varphi }^4$   (2)

is the classical potential. In this paper, we will refer to this potential as the Higgs potential.

It is vital to at this stage to mention that the realisation of the Higgs mechanism is only feasible when considering certain conditions.² The most crucial one is that the quadratic mass term in the Higgs potential must be an ad-hoc tuned such that the classical potential becomes modified into

$V\left(\varphi \right)=-\frac{1}{2}{\mu }^2{\varphi }^2+\frac{\lambda }{4!}{\varphi }^4$   (3)

In this paper, our ad-hoc choice takes the form

$-{\mu }^2=m^2$   (4)

This deliberate choice makes it analytically convenient for the purpose of triggering SSB. Despite this great advantage, the same choice gives rise to the infamous gauge Hierarchy Problem. This is because in the SM, the Higgs mechanism’s ad-hoc adjusted mass term is the only one having a dimensional constant. Being problematic here entails the SM approach to the analysis of SSB particularly the understanding of fundamental electroweak scale.

The above conundrum makes us look for alternative approaches to SSB analysis which may be a good treatment for the short-comings described above. Other scholars have shown that via radiative corrections for vanishing $\mu$ , SSB can take place. In simple terms, the implication of implies that the Coleman-Weinberg mechanism provides us with a consideration of the squared mass term that is irrelevant in bringing about SSB. Above all, the groundbreaking works done by Coleman and Weinberg gave rise to an important tool into the arena of theoretical Nuclear and Particle Physics.

Mathematically, the Coleman-Weinberg Potential can be expressed as

$V_e{}_{ff}({\varphi }_v)=V({\varphi }_v)-\frac{i\hslash }{2}{\displaystyle \int \frac{d^{4}k}{{(2\pi )}^4}}ln[\frac{k^2-V"({\varphi }_v)}{k^2}+\mathcal{O}({\hslash }^2).$   (5)

Despite the Coleman-Weinberg Potential being a great tool in theoretical Nuclear and Particle Physics, documentations of its application to the field of study is marred with ambivalence leading slowly to fears for its redundancy. In this paper, we shall allay this fear via a demonstration that the Coleman-Weinberg Potential has a high likelihood to persist as a very important area of study especially in the field of theoretical Nuclear and Particle Physics. Firstly, we conduct a review of the application of the Coleman-Weinberg Potential in view of SSB analysis. Secondly, the paper considers prospects of resolving the gauge Hierarchy Problem using the Coleman-Weinberg Potential as an analytical tool.

Application of the Coleman-Weinberg potential in the analysis of SSB

In this section, we apply the Coleman-Weinberg Potential to the analysis of SSB by developing a formalism tailored at making our computations easier. By recalling Equation 5, it is clear that the second term on the right hand side of the equation reveals the divergence of the integral. This implies that, in order to progress in our computations, we need to employ dimensional regularization as a facilitating tool.^3-6 This technique brings on board a convenient approach to circumventing divergence challenges.

Under dimensional regularization, the beginning point is to extend the dimensions to D, requiring that the integral measure $\frac{d^{4}k}{{(2\pi )}^4}$  is replaced by

$\frac{d^{D}k}{{(2\pi )}^D}{M}^{4-D}$   (6)

where $M$ is the well-known renormalization scale. Furthermore, the Coleman-Weinberg potential is modified by the extension of dimensions to D and the result takes a structure under Equation 7.

$V_e{}_{ff}({\varphi }_v)=V({\varphi }_v)-\frac{i\hslash M^{4-D}}{2}\int \frac{d^{D}k}{{(2\pi )}^D}ln\left[\frac{k^2-V"\left({\varphi }_v\right)}{k^2}\right]+\mathcal{O}\left({\hslash }^2\right)$   (7)

In order to ease our computations, we proceed via a scientific guess by arbitrarily defining the relation

$\frac{V^{″}\left({\varphi }_v\right)}{k^2}=1+m^2-k^2$   (8)

which allows us to write

$\frac{k^2-V^{″}\left({\varphi }_v\right)}{k^2}=k^2-m^2$   (9)

By combining Equations 7 and 8 we obtain

$\begin{array}{cc}{V}_{eff}\left({\varphi }_v\right)& =V\left({\varphi }_v\right)\frac{i\hslash M^{4-D}}{2}-\frac{d^{D}k}{{(2\pi )}^D}\text{ln}\int \left(k^2-m^2\right)+\mathcal{O}\left({\hslash }^2\right)\\ & =V\left({\varphi }_v\right)-\frac{\hslash M^4}{2{(4\pi )}^{\frac{D}{2}}}\Gamma \left(-\frac{D}{2}\right){(\frac{m^2}{M^2})}^{\frac{D}{2}}\end{array}$   (10)

which satisfies

$\begin{array}{cc}\int \frac{d^{D}k}{{(2\pi )}^D}ln\left(k^2-m^2\right)& =\frac{d}{d\alpha }\int \frac{d^{D}k}{{(2\pi )}^D}\frac{1}{{(k^2-m^2)}^{\alpha }}{|}_{\alpha =0}\\ & =-\frac{i}{2}\frac{1}{{(4\pi )}^{\frac{D}{2}}}\Gamma \left(-\frac{D}{2}\right){(m^2)}^{\frac{D}{2}}\end{array}$   (11)

In order to detect the divergence that is still persistence in Equation 10, we make use of the gamma function shown in Equation 12.

$\Gamma \left(-\frac{D}{2}\right)\approx \frac{1}{\left(4-D\right)}-\frac{\gamma }{2}+\frac{3}{4}$   (12)

Here, in order to absorb the divergence, we use a substitution

$D=4-2ϵ,$   (13)

followed by expansion in terms of ϵ. Thus, Equation 10 becomes

$V_{eff}\left({\varphi }_v\right)=V\left({\varphi }_v\right)-\frac{1}{4}\frac{m^4}{{(4\pi )}^2}\left(\frac{1}{\widetilde{ϵ}}-ln\frac{m^2}{M^2}\right)$   (14)

which, after further manipulation, results in the renormalized effective potential of the form

$V_{eff}\left({\varphi }_v\right)=V\left({\varphi }_v\right)+\frac{1}{4}\frac{m^4}{{(4\pi )}^2}ln\left(\frac{m^2}{M^2}\right)$   (15)

By evoking Equation 3 and plugging the modified classical potential into Equation 15 we obtain

$V_{eff}\left({\varphi }_v\right)=-\frac{1}{2}{\mu }^2{\varphi }_v^2+\frac{\lambda }{4!}{\varphi }_v^4+\frac{1}{4}\frac{m^4}{{(4\pi )}^2}ln\left(\frac{m^2}{M^2}\right)$   (16)

Furthermore, we define an effective mass of a scalar particle⁶ using the relation

$m^2={\mu }^2+3\lambda {\varphi }_v^2$   (17)

which simplifies to Equation 18 upon assuming a vanishing $\mu$ such that

$m^2=3\lambda {\varphi }_v^2$   (18)

Combining Equations 16 and 18 yields

$V_{eff}\left({\varphi }_v\right)=\frac{\lambda }{4}{\varphi }_v^4\left[\frac{1}{3!}+\frac{9\lambda }{{(4\pi )}^2}ln\left(\frac{3\lambda {\varphi }_v^2}{M^2}\right)\right]$   (19)

The result obtained in Equation 19 is a one-loop effective potential under the ${\varphi }^4$ theory of a real scalar field with $\mu =0$ . Now, for analytical convenience, we rewrite the result in Equation 19 as

$V_{eff}\left({\varphi }_v\right)=\mathcal{A}{\varphi }_v^4+ℬ{\varphi }_v^{4}ln\left[\mathcal{C}{\varphi }_v^2\right]$   (20)

where with $\mathcal{A}$ ,$ℬ$ and $\mathcal{C}$ are arbitrarily given by

$\mathcal{A}=\frac{\lambda }{24}, ℬ=\frac{9{\lambda }^2}{64{\pi }^2} and \mathcal{C}=\frac{3\lambda }{M^2}$   (21)

respectively. Armed with the new form of our result described in Equation 20, we can compute its extrema starting with its differential form with respect to ${\varphi }_v$ leading to

$\frac{\partial V_{eff}\left({\varphi }_v\right)}{\partial {\varphi }_v}=4{\varphi }_v^3\left(\mathcal{A}+ℬ\left[ln\left(\mathcal{C}{\varphi }_v^2\right)+\frac{1}{2}\right]\right).$   (22)

In order to obtain the extrema, the derivative under Equation 22 must vanish. Thus, we have

$\frac{\partial V_{eff}\left({\varphi }_v\right)}{\partial {\varphi }_v}=0$   (23)

The solutions to Equation 23 are

${\varphi }_v=0,\pm \mathcal{V}{e}^{\mathcal{W}}$   (24)

With $v$ and $w$ respectively defined as

$\mathcal{V}={(\frac{1}{\mathcal{C}})}^{\frac{1}{2}} and \mathcal{W}=-\frac{1}{2}\left(\frac{\mathcal{A}}{ℬ}+\frac{1}{2}\right)$   (25)

It is vividly clear from our result in Equation 24 that the total number of vacuum expectation values is three, with one being a null vacuum expectation (local maximum) value and the other two non-zero being vacuum expectation values (two minima).     The occurrence of the non-zero expectation values described in Equation 26 triggers SSB.

${\varphi }_v=\pm \mathcal{V}{e}^{\mathcal{W}}$   (26)

This result can be graphically presented as illustrated in Figure 1.

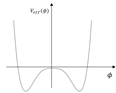
Figure 1 Results for SSB.

These results obtained here point to something very important in Nuclear and Particle Physics. In order to trigger SSB, unlike the Higgs mechanism, the Coleman-Weinberg Potential does not need to take into account the squared mass term of the classical potential. This entails that the Coleman-Weinberg Potential has the capacity to undergo transformation without losing its applicability in SSB analysis. Therefore, this adds to the Coleman-Weinberg Potential a dimension of versatility leading to its persistence which is highly likely to render its relevant even in the emerging NP.

Hierarchy problem prospects

At one-loop correction and without considering an ad-hoc squired mass term, the Coleman-Weinberg mechanism gives mass to the Higgs boson. As a result, it is without exaggeration to mention that the possibility of solving the Hierarchy Problem using the Coleman-Weinberg Potential is not far-fetched. This is because in the Higgs potential, the only term with a dimensional constant is the squired mass term.

To begin with, the second derivative of the Coleman-Weinberg Potential is given by

$\frac{{\partial }^2{V}_{eff}\left({\varphi }_v\right)}{\partial {\varphi }_v^2}=2{\varphi }_v^2\left(6\mathcal{A}+ℬ\left[6ln\left(\mathcal{C}{\varphi }_v^2\right)+7\right]\right)$   (27)

We can use Equation 27 to predict the Higgs mass by computing its values at minimum points as described in Equation 28.

$\frac{{\partial }^2{V}_{eff}\left({\varphi }_v\right)}{\partial {\varphi }_v^2}{|}_{{\varphi }_v=\mathcal{V}{e}^{\mathcal{W}}}$   (28)

On one hand, by solving equation 28 we are able to determine that

$m_H\approx {(\frac{1}{2}\frac{{\partial }^2{V}_{eff}\left({\varphi }_v\right)}{\partial {\varphi }_v^2}{|}_{{\varphi }_v=\mathcal{V}{e}^{\mathcal{W}}})}^{\frac{1}{2}}\approx 10GeV$   (29)

On the other hand, experimental results at ATLAS ad CMS collaborators at the LHC, as indicated in Equation 30, have however shown a very huge disparity between experiments and theory.⁷

$m_H\approx 125GeV$   (30)

The huge significant disparity of the results in Equations 29 and 30 is the main source of the gauge Hierarchy Problem.  This makes our probe to solve the Hierarchy Problem via the Coleman-Weinberg Potential to be futile. However, not all hope is lost yet and we must keep believing that the Coleman-Weinberg mechanism may provide a clue leading to a breakthrough solution to the Hierarchy Problem which is not completely enigmatic. Thus, the Coleman-Weinberg Potential must be revisited with a more complicated framework.

In this paper, firstly, we have  shown that SSB induced by the Coleman-Weinberg mechanism can occur even  when  is zero, contradicting SSB in SM. Secondly, we can conclude that the Coleman-Weinberg Potential has a higher chance of being a possible solution to the Hierarchy Problem.  Despite it being futile, abandoning this theory is far-fetched at the moment and persistence may lead to resolving the Hierarchy Problem. In a nutshell, the Coleman-Weinberg Potential will continue to maintain its status as a topic of sustained interest in the field of theoretical Nuclear and Particle Physics.

None.

1. Aitchison I Jr, Hey AJG. Gauge theories in particle physics: a practical introduction. London: Taylor & Francis Group. 2013.
2. S Coleman, E Weinberg. Radiative corrections as the origin of spontaneous symmetry breaking. Phys Rev. 1973;1888.
3. Strickland M. Relativistic quantum field theory: canonical formalism. Kent: Morgan & Clayton Publishers. 2019.
4. Fradkin E. Quantum field theory: an integrated approach. Oxford shire: Princeton University Press. 2021.
5. Peskin ME, Schroeder DV. An introduction to quantum field theory. London: Taylor & Francis Group. 2018.
6. Martinez AB. Coleman–Weinberg Symmetry Breaking and Higgs Physics. University of Barcelona. 2019.
7. C Wetter–rich, M Yamada. Gauge hierarchy problem in asymptotically safe gravity – the resurgent mechanism. Physics Letters B. 2017;770.
8. S Bhattacarjee, P Majumdar. Gravitational Coleman–Weinberg Potential and its Temperature counterpart. Physics Letters B. 2014;885.
9. Weinberg S. Foundations of modern Physics. Cambridge. Cambridge: University Press. 2021.
10. Srednicki M. Quantum field Theory. Cambridge: Cambridge University Press. 2007.
11. OECD (Organisation for Economic Co–operation and Development). OECD Policy Brief No. 8, OECD, Paris, France, 2005.
12. OECD (Organisation for Economic Co–operation and Development). The OECD Three–Year Project on Sustainable Development: A Progress Report, OECD, Paris, France, 2015.
13. IEA (International Energy Agency). Key World Energy Statistics from the IEA – Data for 1996, IEA, Paris, France, 2018.
14. Rhodes R, Beller D, The Need for Nuclear Power, in Foreign Affairs, Washington, United States, 2000;79(1).
15. World–watch Institute. State of the World 1999, W.W. Norton &Company Inc., United States. 2009.
16. IEA (International Energy Agency). World Energy Outlook, OECD, Paris, France, 2009.
17. IEA (International Energy Agency). Energy Balances of Non–OECD Countries – 1999 Edition, OECD, Paris, France, 2001.
18. NEA (OECD Nuclear Energy Agency). Nuclear Energy Data, Paris, France, 2000.9. IAEA (International Atomic Energy Agency), 2000, Nuclear Power Reactors in the World, Vienna, Austria.
19. IIASA (International Institute for Applied Systems Analysis) and WEC(World Energy Council), (2008), Global Energy Perspectives to 2050and Beyond, WEC, London, United Kingdom.
20. Nuclear energy and sustainable development.
21. Cheng Zhang, Manyika Kabuswa Davy, Yu Shi, et al. Multiparticle azimuthal angular correlations in pA collisions. Physical Review D. 2019;99:034009.
22. Manyika Kabuswa Davy, Cyrille Marquet, Yu Shi, et al. Two particle azimuthal harmonics in pA collisions. Nuclear Physics A. 2018;983(18).
23. Manyika Kabuswa Davy, Matindih Kahyata Levy. On the Radiation of Gluon Jets: A Summary. 2019.
24. Manyika Kabuswa Davy, Nawa Nawa. On the Future of Nuclear Energy and Climate Change: A Summary. 2019.
25. Davy MK, Hamweendo A, Banda PJ, et al. On radiation protection and climate change – a summary. Phys Astron Int J. 2022;6(3):126–129.
26. SR Coleman, EJ Weinberg. Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys Rev. 1973;1888.
27. Davy MK, Banda PJ, Morris MK, et al. Nuclear energy and sustainable development. Phys Astron Int J. 2022;6(4):142‒143.
28. Matindih LK, Moyo E, Manyika DK. Some Results of Upper and Lower M–Asymmetric Irresolute Multifunctions in Bitopological Spaces. Advances in Pure Mathematics. 2021;11;611–627.