From the model of interstitial alloy AB with FCC structure and the condition of absolute stability for crystalline state we derive analytic expression for the temperature of absolute stability for crystalline state, the melting temperature and the equation of melting curve of this alloy by the way of applying the statistical moment method. The obtained results allow us to determine the melting temperature of alloy AB ant zero pressure and under pressure. In limit cases, we obtain the melting theory of main metal A with FCC structure. The theoretical results are numerically applied for alloys AuSi and AgSi.

Keywords: interstitial alloy, absolute stability of crystalline state, statistical moment method

Alloys in general and interstitial alloys in particular are typical materials in material technology and science. Study on interstitial alloys pays particular attention to many researchers. The melting temperature (MT) of materials under pressure is a very important problem of solid state physics and material science.^1–3 Theoretically in order to determine the MT of crystal it is necessary to apply the equilibrium condition of solid phase and liquid phase. By this way, there are some methods such as the self–consistent phonon field method and the one–particle distribution function method. The obtained results from these methods are in not good agreement with experiments and are limited at low pressures.

In aid of the statistical moment method (SMM), Tang & Hung^4,5 show that we absolutely only use the solid phase of crystal to determine the MT. The obtained results from the SMM are better than that from other methods in comparison with experiments.

Analytic result

In the model of AB interstitial alloy with the face–centured cubic (FCC) structure, the A atoms with large size stay in the peaks and the face centers of cubic unit cell and the C interstitial atoms with smaller size stay in the body center. In^6,7 we derived the analytic expressions of the nearest neighbor distance, the cohesive energy and the alloy parameters for atoms B, A, A₁ (the atom A in the face centers) and A₂ (the atom A in the peaks).

The equation of state of the AB interstitial aloy with FCC structure at temperature T and pressure P is described by

$Pv=-r_1\left(\frac{1}{6}\frac{\partial u_0}{\partial r_1}+\theta x\mathrm{cth}x\frac{1}{2k}\frac{\partial k}{\partial r_1}\right)$  (1)

At 0K and pressure P, this equation has the form

$Pv=-r_1\left(\frac{\partial u_0}{\partial r_1}+\frac{\hslash {\omega }_0}{4k}\frac{\partial k}{\partial r_1}\right).$  (2)

Knowing the form of the interaction potential${\phi }_{i0}$ ,equation (1) allows os to determine the nearest neighbor distance$r_{1X}\left(P,0\right)\left(X=B,A,A_1,A_2\right)$ at 0K and pressure P. Knowing$r_{1X}\left(P,0\right)$ we can determine the parameters$k_X(P,0),{\gamma }_{1X}(P,0),{\gamma }_{2X}(P,0),{\gamma }_X(P,0)$ at 0K and pressure P for each case of X. The displacement$y_{0X}(P,T)$ of atoms from the equilibrium position at temperature T and pressure P is determined.^6,7 From that, we can calculate the neares neighbor distance$r_{1X}\left(P,T\right)$ at temperature T and pressure P as follows

$r_{1C}(P,T)=r_{1C}(P,0)+y_{A_1}(P,T),r_{1A}(P,T)=r_{1A}(P,0)+y_A(P,T),$

$r_{1A_1}(P,T)\approx r_{1C}(P,T),r_{1A_2}(P,T)=r_{1A_2}(P,0)+y_C(P,T).$  (3)

The mean neares neighbor distance between two atoms in AB interstitial alloy with FCC structure is approximately determined by

$\overline{r_{1A}\left(P,T\right)}=\overline{r_{1A}\left(P,0\right)}+\overline{y\left(P,T\right)},$

$\overline{r_{1A}(P,0)}=\left(1-c_B\right)r_{1A}(P,0)+c_B{r^{\prime }}_{1A}(P,0),{r^{\prime }}_{1A}(P,0)=\sqrt{2}{r}_{1B}(P,0),$

$\overline{y\left(P,T\right)}=\left(1-15c_B\right)y_A\left(P,T\right)+c_B{y}_B\left(P,T\right)+6c_B{y}_{A_1}\left(P,T\right)+8c_B{y}_{A_2}\left(P,T\right).$  (4)

The free energy of AB interstitial alloy with FCC structure and concetration condition$c_B<<c_A$ has the form

${\psi }_{AB}=\left(1-15c_B\right){\psi }_A+c_B{\psi }_B+6c_B{\psi }_{A_1}+8c_B{\psi }_{A_2}-T{S}_c.$

${\psi }_X\approx U_{0X}+{\psi }_{0X}+3N\{\frac{{\theta }^2}{k_X^2}\left[{\gamma }_{2X}{X}_X^2-\frac{2{\gamma }_{1X}}{3}\left(1+\frac{X_X}{2}\right)\right]+$

$+\frac{2{\theta }^3}{k_X^4}\left[\frac{4}{3}{\gamma }_{2X}^2{X}_X\left(1+\frac{X_X}{2}\right)-2\left({\gamma }_{1X}^2+2{\gamma }_{1X}{\gamma }_{2X}\right)\left(1+\frac{X_X}{2}\right)\left(1+X_X\right)\right]\},$

${\psi }_{0X}=3N\theta \left[x_X+\ln (1-e^{-2x_X})\right],X_X\equiv x_X\coth x_X,$  (5)

where${\psi }_A$ is the free energy of A atom in A pure metal,${\psi }_B$ is the free energy of B atom in interstitial alloy,${\psi }_{A_1}$  and${\psi }_{A_2}$ respectively are free energy of A₁ and A₂ atoms and S_c is the configuration entropy of AC interstitial alloy.

The pressure is calculated by

$P=-{\left(\frac{\partial \psi }{\partial V}\right)}_T=-\frac{a}{3V}{\left(\frac{\partial \psi }{\partial a}\right)}_T.$  (6)

Setting

${\gamma }_G^T=-\frac{a_{AB}}{6}[\frac{1}{k_A}\frac{\partial k_A}{\partial a_A}\left(1-15c_B\right)x_A\coth x_A+\frac{1}{k_B}\frac{\partial k_B}{\partial a_B}{c}_B{x}_B\coth x_B+$
$+\frac{1}{k_{A_1}}\frac{\partial k_{A_1}}{\partial a_{A_1}}6c_B{x}_{A_1}\coth x_{A_1}+\frac{1}{k_{A_2}}\frac{\partial k_{A_2}}{\partial a_{A_2}}8c_B{x}_{A_2}\coth x_{A_2}].$  (7)

Here,${\gamma }_G^T$ is the Grüneisen parameter of ABalloy. Then,

$P=-\frac{a_{AB}}{6V_{AB}}\left[\left(1-15c_B\right)\frac{\partial U_{0A}}{\partial a_A}+c_B\frac{\partial U_{0B}}{\partial a_B}+6c_B\frac{\partial U_{0A_1}}{\partial a_{A_1}}+8c_B\frac{\partial U_{0A_2}}{\partial a_{A_2}}\right]+\frac{3{\gamma }_G^T.\theta }{V_{AB}}.$ (8)

From the condition of absolute stability limit

${\left(\frac{\partial P}{\partial V_{AB}}\right)}_T=0$  hay ${\left(\frac{\partial P}{\partial a_{AB}}\right)}_T=0$ (9)

we can derive the absolute stability temperature for crystalline state in the form

$\begin{array}{l}{T}_s=\frac{T{S}_1}{M{S}_1},T{S}_1=2P{V}_{AB}+\frac{a_{AB}^2}{6}\left[\left(1-15c_B\right)\frac{{\partial }^2{U}_{0A}}{\partial a_A^2}+c_B\frac{{\partial }^2{U}_{0B}}{\partial a_B^2}+6c_B\frac{{\partial }^2{U}_{0A_1}}{\partial a_{A_1}^2}+8c_B\frac{{\partial }^2{U}_{0A_2}}{\partial a_{A_2}^2}\right]-\\ -\left(1-15c_B\right)\left[\frac{a_{AB}}{2k_A}{\left(\frac{\partial k_A}{\partial a_A}\right)}^2-a_{AB}\frac{{\partial }^2{k}_A}{\partial a_A^2}\right]\frac{\hslash {\omega }_A{a}_{AB}}{4k_A}-c_B\left[\frac{a_{AB}}{2k_B}{\left(\frac{\partial k_B}{\partial a_B}\right)}^2-a_{AB}\frac{{\partial }^2{k}_B}{\partial a_B^2}\right]\frac{\hslash {\omega }_B{a}_{AB}}{4k_B}-\end{array}$

$-6c_B\left[\frac{a_{AB}}{2k_{A_1}}{\left(\frac{\partial k_{A_1}}{\partial a_{A_1}}\right)}^2-a_{AB}\frac{{\partial }^2{k}_{A_1}}{\partial a_{A_1}^2}\right]\frac{\hslash {\omega }_{A_1}{a}_{AB}}{4k_{A_1}}-8c_B\left[\frac{a_{AB}}{2k_{A_2}}{\left(\frac{\partial k_{A_2}}{\partial a_{A_2}}\right)}^2-a_{AB}\frac{{\partial }^2{k}_{A_2}}{\partial a_{A_2}^2}\right]\frac{\hslash {\omega }_{A_2}{a}_{AB}}{4k_{A_2}},$

$M{S}_1=\left(1-15c_B\right)\frac{a_{AB}^2{k}_{Bo}}{4k_A^2}{\left(\frac{\partial k_A}{\partial a_A}\right)}^2+c_B\frac{a_{AB}^2{k}_{Bo}}{4k_B^2}{\left(\frac{\partial k_B}{\partial a_B}\right)}^2+6c_B\frac{a_{AB}^2{k}_{Bo}}{4k_{A_1}^2}{\left(\frac{\partial k_{A_1}}{\partial a_{A_1}}\right)}^2+8c_B\frac{a_{AB}^2{k}_{Bo}}{4k_{A_2}^2}{\left(\frac{\partial k_{A_2}}{\partial a_{A_2}}\right)}^2,$ (10)

In the case of zero pressure,

$T_s=\frac{T{S}_2}{M{S}_2},T{S}_2=\frac{a_{AB}^2}{6}\left[\left(1-15c_B\right)\frac{{\partial }^2{U}_{0A}}{\partial a_A^2}+c_B\frac{{\partial }^2{U}_{0B}}{\partial a_B^2}+6c_B\frac{{\partial }^2{U}_{0A_1}}{\partial a_{A_1}^2}+8c_B\frac{{\partial }^2{U}_{0A_2}}{\partial a_{A_2}^2}\right]-$

$\begin{array}{l}-\left(1-15c_B\right)\left[\frac{a_{AB}}{2k_A}{\left(\frac{\partial k_A}{\partial a_A}\right)}^2-a_{AB}\frac{{\partial }^2{k}_A}{\partial a_A^2}\right]\frac{\hslash {\omega }_A{a}_{AB}}{4k_A}-c_B\left[\frac{a_{AB}}{2k_B}{\left(\frac{\partial k_B}{\partial a_B}\right)}^2-a_{AB}\frac{{\partial }^2{k}_B}{\partial a_B^2}\right]\frac{\hslash {\omega }_B{a}_{AB}}{4k_B}-\\ -6c_B\left[\frac{a_{AB}}{2k_{A_1}}{\left(\frac{\partial k_{A_1}}{\partial a_{A_1}}\right)}^2-a_{AB}\frac{{\partial }^2{k}_{A_1}}{\partial a_{A_1}^2}\right]\frac{\hslash {\omega }_{A_1}{a}_{AB}}{4k_{A_1}}-9c_B\left[\frac{a_{AB}}{2k_{A_2}}{\left(\frac{\partial k_{A_2}}{\partial a_{A_2}}\right)}^2-a_{AB}\frac{{\partial }^2{k}_{A_2}}{\partial a_{A_2}^2}\right]\frac{\hslash {\omega }_{A_2}{a}_{AB}}{4k_{A_2}},\end{array}$

$M{S}_2=\left(1-15c_B\right)\frac{a_{AB}^2{k}_{Bo}}{4k_A^2}{\left(\frac{\partial k_A}{\partial a_A}\right)}^2+c_B\frac{a_{AB}^2{k}_{Bo}}{4k_B^2}{\left(\frac{\partial k_B}{\partial a_B}\right)}^2+6c_B\frac{a_{AB}^2{k}_{Bo}}{4k_{A_1}^2}{\left(\frac{\partial k_{A_1}}{\partial a_{A_1}}\right)}^2+8c_B\frac{a_{AB}^2{k}_{Bo}}{4k_{A_2}^2}{\left(\frac{\partial k_{A_2}}{\partial a_{A_2}}\right)}^2,$ (11)

Because the curve of absolute stability limit for crystalline state is not far from the MS of crystal, the T_s temperature usually is large and$x_X\coth x_X\approx 1$ at$T_s$ . Therefore,

$\frac{1}{\left(1-15c_B\right)\frac{a_{AB}^2{k}_{Bo}}{4k_A^2}{\left(\frac{\partial k_A}{\partial a_A}\right)}^2+c_B\frac{a_{AB}^2{k}_{Bo}}{4k_B^2}{\left(\frac{\partial k_B}{\partial a_B}\right)}^2+6c_B\frac{a_{AB}^2{k}_{Bo}}{4k_{A_1}^2}{\left(\frac{\partial k_{A_1}}{\partial a_{A_1}}\right)}^2+8c_B\frac{a_{AB}^2{k}_{Bo}}{4k_{A_2}^2}{\left(\frac{\partial k_{A_2}}{\partial a_{A_2}}\right)}^2}\times$

$\begin{array}{l}\times \{2P{V}_{AB}+\frac{a_{AB}^2}{6}\left[\left(1-15c_B\right)\frac{{\partial }^2{U}_{0A}}{\partial a_A^2}+c_B\frac{{\partial }^2{U}_{0B}}{\partial a_B^2}+6c_B\frac{{\partial }^2{U}_{0A_1}}{\partial a_{A_1}^2}+8c_B\frac{{\partial }^2{U}_{0A_2}}{\partial a_{A_2}^2}\right]-\\ -\left(1-15c_B\right)\left[\frac{a_{AB}}{2k_A}{\left(\frac{\partial k_A}{\partial a_A}\right)}^2-a_{AB}\frac{{\partial }^2{k}_A}{\partial a_A^2}\right]\frac{\hslash {\omega }_A{a}_{AB}}{4k_A}-c_B\left[\frac{a_{AB}}{2k_B}{\left(\frac{\partial k_B}{\partial a_B}\right)}^2-a_{AB}\frac{{\partial }^2{k}_B}{\partial a_B^2}\right]\frac{\hslash {\omega }_B{a}_{AB}}{4k_B}-\end{array}$

$-6c_B\left[\frac{a_{AB}}{2k_{A_1}}{\left(\frac{\partial k_{A_1}}{\partial a_{A_1}}\right)}^2-a_{AB}\frac{{\partial }^2{k}_{A_1}}{\partial a_{A_1}^2}\right]\frac{\hslash {\omega }_{A_1}{a}_{AB}}{4k_{A_1}}-8c_B\left[\frac{a_{AB}}{2k_{A_2}}{\left(\frac{\partial k_{A_2}}{\partial a_{A_2}}\right)}^2-a_{AB}\frac{{\partial }^2{k}_{A_2}}{\partial a_{A_2}^2}\right]\frac{\hslash {\omega }_{A_2}{a}_{AB}}{4k_{A_2}}\}+$

$+\frac{2V_{AB}}{k_{Bo}{a}_{AB}[\frac{1}{k_A}\frac{\partial k_A}{\partial a_A}\left(1-15c_B\right)+\frac{1}{k_B}\frac{\partial k_B}{\partial a_B}{c}_B+\frac{1}{k_{A_1}}\frac{\partial k_{A_1}}{\partial a_{A_1}}6c_B+\frac{1}{k_{A_2}}\frac{\partial k_{A_2}}{\partial a_{A_2}}8c_B]}\times$

$\times \left\{P+\frac{a_{AB}}{6V_{AB}}\left[\left(1-15c_B\right)\frac{\partial U_{0A}}{\partial a_A}+c_B\frac{\partial U_{0B}}{\partial a_B}+6c_B\frac{\partial U_{0A_1}}{\partial a_{A_1}}+8c_B\frac{\partial U_{0A_2}}{\partial a_{A_2}}\right]\right\}=0.$  (12)

That is the equation for the curve of absolute stability limit for crystalline state. Therefore, the pressure is a function of the mean nearest neighbor distance

$P=P(a_{AB}).$ (13)

Temperature T_s (0) at zero pressure has the form

$T_s(0)=\frac{a_{AB}}{18{\gamma }_G^T{k}_{Bo}}\left[\left(1-15c_B\right)\frac{\partial U_{0A}}{\partial a_A}+c_B\frac{\partial U_{0B}}{\partial a_B}+6c_B\frac{\partial U_{0A_1}}{\partial a_{A_1}}+8c_B\frac{\partial U_{0A_2}}{\partial a_{A_2}}\right]$  (14)

where the parameters$a_{AB},\frac{\partial U_{0X}}{\partial a_X},{\gamma }_G^T$ are determined at $T_s(0)$ . Temperature T_s at pressure P has the form

$T_s\approx T_s(0)+\frac{V_{AB}P}{3k_{Bo}{\left({\gamma }_G^T\right)}^2}{\left(\frac{\partial {\gamma }_G}{\partial T}\right)}_{a_{AB}}{T}_s.$  (15)

Here,$k_{Bo}$ is the Boltzmann constant,$V_{ABC},{\gamma }_G^T,\partial {\gamma }_G^T/\partial T$ dare determined at$T_s$ . Approximately,$T_m\approx T_s$ . In order to solve equation (15), we can use the approximate iteration method. In the first approximate iteration,

$T_{s1}\approx T_s(0)+\frac{V_{AB}(T_s(0))P}{3k_{Bo}{\gamma }_G(T_s(0))}.$  (16)

Here$T_s(0)$ is the temperature of absolute stability limit for crystalline state at pressure P in the first approximate iteration of equation (15). Substituting T_s1 into equation (15), we obtain the better approximate value T_s2 of T_s at pressure P in the second approximate iteration

$T_{s2}\approx T_s(0)+\frac{V_{AB}(T_{s1})P}{3k_{Bo}{\gamma }_G(T_{s1})}-\frac{V_{AB}(T_{s1})P}{3k_{Bo}{\gamma }_G^2(T_{s1})}{\left(\frac{\partial {\gamma }_G}{\partial T}\right)}_{a_{AB}}{T}_{s1}.$ (17)

Analogouslty, we can obtain the better approximate values $T_{s3},T_{s4},\mathrm{...}$  of T_s at pressure P in the thierd, fourth, etc. approximate iterations. These approximations are applyed at low pressures.

In the case of high pressure, the MT of alloy at pressure P is calculated by

$T_m(P)=\frac{T_m(0)B_0{}^{\frac{1}{{B^{\prime }}_0}}}{G(0)}.\frac{G(P)}{{(B_0+{B^{\prime }}_{0}P)}^{\frac{1}{{B^{\prime }}_0}}},$  (18)

where$T_m(P)$ and$T_m(0)$ respectively are the MT at pressure P and zero pressure,$G(P)$ and$G(0)$ respectively are the rigidity bulk modulus at pressure P and zero pressure,$B_0$ is the isothermal elastic modulus at zero pressure, ${B^{\prime }}_0={\left(\frac{d{B}_T}{dP}\right)}_{P=0},B_T=B_T(P)$ is the isothermal elastic modulus at pressure.

Numerical results for alloys AuSi and AgSi
For alloys AuSi and AgSi, we use the n–m pair potential

$\phi (r)=\frac{D}{n-m}\left[m{\left(\frac{r_0}{r}\right)}^n-n{\left(\frac{r_0}{r}\right)}^m\right],$  (19)

where potential parameters are given in Table 1.⁸

Considering the interaction between atoms Au(Ag) and Si in the above mentioned alloys, we use the potential (19) but calculating approximately$\overline{D}=\sqrt{D_{\text{Au(Ag)}}{D}_{\text{Si}}},{\overline{r}}_0=\sqrt{r_{0\text{Au(Ag)}}{r}_{0\text{Si}}}$ . Parameters$\overline{m}$ and$\overline{n}$ are taken empirically.

At 0.1 MPa, Au has a FCC structure with$a=4,{0785.10}^{-10}\text{m}$ at 300K and the melting point at 1337 K. The melting curve of Au is determined up to 1673 K and 6.5 GPa with the slope dT/dP = 60 K/GPa^9,10 and up to 1923 K and 12 Gpa.¹¹

At 0.1 MPa, Ag has a FCC structure with$a=4,{0862.10}^{-10}\text{m}$ at 300K and the melting point at 1235 K. The melting curve of Au is determined up to 1563 K and 6.5 GPa with the slope dT/dP = 60 K/Gpa.⁹

Our numerical results are summarized in tables from Table 2 to Table 3 and illustrated in figures from Figure 1 to Figure 2. The concentration of interstitial atoms changes from 0 to 5% and the pressure changes from 0 to 10 GPa for Au and from 0 to 6 GPa for Ag.

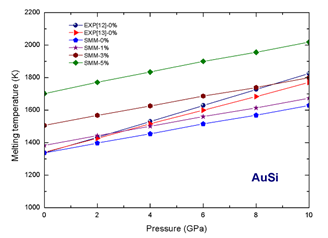
Figure 1 Dependence of melting temperature on pressure and concentration of interstitial atoms for alloy AuSi.

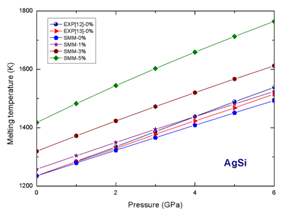
Figure 2 Dependence of melting temperature on pressure and concentration of interstitial atoms for alloy AgSi.

According to our numerical results for alloy AuSi at the same concentration of interstitial atoms Si when pressure increases, the melting temperature increases. For example at$c_{\text{Si}}=5\%$ when P increases from 0 to 10 GPa,$T_{\text{melting}}$ of alloy AuSi increases from 1701.8 K to 2018.94 K. At the same pressure when the concentration of interstitial atoms Si increases, the melting temperature increases. For example at P=10 GPa, when$c_{\text{Si}}$ increases from 0 to 5%, $T_{\text{melting}}$ of alloy AuSi increases from 11629.22 K to 2018.94K.

According to our numerical results for alloy AgSi at the same concentration of interstitial atoms Si when pressure increases, the melting temperature increases. For example at$c_{\text{Si}}=5\%$ when P increases from 0 to 6 GPa,$T_{\text{melting}}$ of alloy AgSi increases from 1418.12 K to 1764.81 K. At the same pressure when the concentration of interstitial atoms Si increases, the melting temperature increases. For example at P=6 GPa, when$c_{\text{Si}}$ increases from 0 to 5%,$T_{\text{melting}}$ of alloy AuSi increases from 1492.95 K to 1764.81K (Table 3).

At zero concentration of interstitial atoms Si, the melting temperature of alloys AuSii and AgSi respectively becomes the melting temperature of metals Au and Ag. The melting temperature of substitution alloys AuCu and AgCu is smaller than the melting temperature of metals Au and Ag, respectively. The dependences of melting temperature on pressure and concentration ò interstirtial atoms Si for alloy AuSi and AgSi are shown in (Figure 1) (Figure 2).

The calculated results for the melting temperature of metals Au and Ag are in goog agreement with the experimental data¹² (deviation is about sereral percents) (Table 4) (Table 5).

In aid of the SMM, we derive the analytic expressions of the temperature of absolute stability limit for crystalline state and the melting temperature together with the melting curve of the binary interstitial alloy depending on pressure and concentration of interstitial atoms. In limit case, we obtain the melting theory of main metal with FCC structure. The theoretical results are numerically applied for alloys AuSi and AgSi.

None.

Author declares there is no conflict of interest.

1. Belonoshko AB, Simak SI, Kochetov AE, et al. High–pressure melting of molybdenum. Physical Review Letters. 2004;92(19).
2. Burakovsky L, Preston DL, Silbar RR. Analysis of dislocation mechanism for melting of elements: Pressure dependence. Journal of Applied Physics. 2000;88(11):6294–6331.
3. Kumari M, Kumari K, Dass N. Onthe melting law at high pressure. Physica Status Solidi (a). 1987;99(1):22–26.
4. Tang N, Hung VV. Investigation of the thermodynamic properties of anharmonic crystals by the momentum method. I. General results for face–centred cubic crystals. Physica Status Solidi (B). 1998;149(2):511–519.
5. Hung VV, Masuda–Jindo K. Application of statistical moment method to thermodynamic properties of metals at high pressures. Journal of the Physical Society of Japan. 2000;69.
6. Hoc NQ, Tinh BD, Tuan LD, et al. Elastic deformation of binary and ternary interstitial alloys with FCC structure and zero pressure: Dependence on temperature, concentration of substitution atoms and concentration of interstitial atoms. Mathematical and Physical Sciences. 2016;61(7):47–57.
7. Hoc NQ, Vinh DQ, Viet LH. Thermodynamic property of binary interstitial alloy with FCC structure: Dependence on temperature and concentration of interstitial atoms. Vietnam: Report at the 41th National Conference on Theoretical Physics (NCTP–41); 2016.
8. Magomedov MN. J Fiz Khimic. 1987;61:1003.
9. Akella J, Kennedy GC. Melting of Au, Ag and Cu–proposal for a new high–pressure calibration scale. Journal of Geophysical Research. 1971;76(20):4969–4977.
10. Mirwald PW, Kennedy GC. The melting curve of Au, Ag and Cu to 60–kbar pressure: A reinvestigation. Journal of Geophysical Research. 1979;84(B12):6750–6756.
11. Sumita T, Kato M, Yoneda A. The thermal analysis in an MA–8 type apparatus: the melting of gold at 12 GPa. The Review of High Pressure Science and Technology. 1998;7:254–256.
12. Tonkov EY, Ponyatovsky EG. Phase transformations of elements under high pressure. USA: CRC Press; 2005.