In this paper, we obtained the structural-parametric model, the matrix transfer function, the static and dynamic characteristics of the multilayer electromagnetoelastic actuator of adaptive optics. It was designed the structural diagram of the multilayer electromagnetoelastic actuator of adaptive optics for composite telescope and astrophysics equipment in contrast to electrical equivalent circuits of the piezotransducer and the vibration piezomotor.

Keywords: multilayer electromagnetoelastic actuator, multilayer piezoactuator, structural diagram, matrix transfer frunction

For the adaptive optics of the composite telescope and the astrophysics equipment we used the multilayer electromagnetoelastic actuator nano and micro displacement with the piezoelectric, piezomagnetic, electrostriction, magnetostriction effects with the range of movement from nanometers to hundred of micrometers.¹⁻³⁰ We received the structural-parametric model, the structural diagram of the multilayer electromagnetoelastic actuator in contrast to the electrical equivalent circuits of the piezotransducer and the vibration piezomotor.^1–11 The matrix transfer function of the multilayer electromagnetoelastic actuator is calculated for the control system of the composite telescope or the interferometer.¹⁴⁻³² We determined the structural-parametric model and the structural diagram of the multilayer actuator using the equation of the electromagnetoelasticity, the equivalent quadripole and the boundary conditions on the faces of the multilayer electromagnetoelastic actuator.

We received the structural diagram of the multilayer electromagnetoelastic actuator of adaptive optics for composite telescope and astrophysics equipment in difference from Cady's and Mason's electrical equivalent circuits of the piezotransducer and the vibration piezomotor. In this work we used the method of the mathematical physics with Laplace transform for the structural-parametric model and the structural diagram of the multilayer electromagnetoelastic actuator for the adaptive optics of the composite telescope in astronomy.^{8,14,19,29,30} We have the equation^{8,9,11,24,29,31} of the electromagnetoelasticity in the form

$S_i={\nu }_{mi}{\Psi }_m+s_{ij}^{\Psi }{T}_j$

where $S_i$  is the relative displacement, ${\nu }_{mi}$ is the coefficient of electromagnetoelasticity in the form $d_{mi}$  piezomodule or magnetostrictive coefficient, ${\Psi }_m$  is control parameter in variables: electric $E_m$ , magnetic $H_m$  field strengths or electric $D_m$  induction, $s_{ij}^{\Psi }$  is the elastic compliance with $\Psi =\text{const}$ , $T_j$  is the mechanical stress, i, j, m are the indexes.

For the multilayer electromagnetoelastic actuator we received the equation of the causes force in the form

$F={\nu }_{mi}{S}_0{\Psi }_m/s_{ij}^{\Psi }$

where $S_0$   is the cross sectional area of the multilayer electromagnetoelastic actuator. The matrix the equivalent quadripole of the multilayer piezoactuator^29,31 has the form

${\left[M\right]}^n=\left[\begin{array}{cc}\text{ch}\left(l\gamma \right)& Z_0\text{sh}\left(l\gamma \right)\\ \frac{\text{sh}\left(l\gamma \right)}{Z_0}& \text{ch}\left(l\gamma \right)\end{array}\right]$

where l is the length for longitudinal $l=n\delta ,$ for transverse $l=nh$ and for shift piezoeffect $l=nb,$  for the piezolayer $\delta ,h,b$ are the thickness, the height, the width, $\gamma$  is the coefficient propagation.

We obtained the structural-parametric model and the structural diagram of the multilayer electromagnetoelastic actuator of adaptive optics for composite telescope and astrophysics equipment on Figure 1 from the equation of the force that causes deformation, the equivalent quadripole and the boundary conditions with the forces on faces of the actuator in the following form

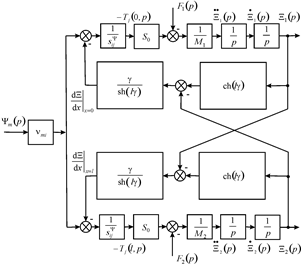
Figure 1 Structural diagram of multilayer electromagnetoelastic actuator for adaptive optics.

$\begin{array}{l}{\Xi }_1\left(p\right)={\left[1/\left(M_1{p}^2\right)\right]}^{}\times \\ \times \left\{-F_1\left(p\right)+{\left(1/{\chi }_{ij}^{\Psi }\right)}_{}^{}\left[{\nu }_{mi}{\Psi }_m\left(p\right)-{\left[\gamma /\text{sh}\left(l\gamma \right)\right]}_{}\left[\text{ch}\left(l\gamma \right){\Xi }_1\left(p\right)-{\Xi }_2\left(p\right)\right]\right]\right\}\end{array}$

$\begin{array}{l}{\Xi }_2\left(p\right)={\left[1/\left(M_2{p}^2\right)\right]}^{}\times \\ \times \left\{-F_2\left(p\right)+{\left(1/{\chi }_{ij}^{\Psi }\right)}_{}^{}\left[{\nu }_{mi}{\Psi }_m\left(p\right)-{\left[\gamma /\text{sh}\left(l\gamma \right)\right]}_{}\left[\text{ch}\left(l\gamma \right){\Xi }_2\left(p\right)-{\Xi }_1\left(p\right)\right]\right]\right\}\end{array}$

where  $v_{mi}=\{\begin{array}{c}{d}_{33},d_{31},d_{15}\\ g_{33},g_{31},g_{15}\\ d_{33},d_{31},d_{15}\end{array}{\Psi }_m=\{\begin{array}{c}{E}_3,E_1\\ D_3,D_1\\ H_3,H_1\end{array}{s}_{ij}^{\Psi }=\{\begin{array}{c}{s}_{33}^E,s_{11}^E,s_{55}^E\\ s_{33}^D,s_{11}^D,s_{55}^D\\ s_{33}^H,s_{11}^H,s_{55}^H\end{array}$ ,

$l={\{\begin{array}{c}\delta \\ h\\ b\end{array}}_{,} c^{\Psi }={\{\begin{array}{c}{c}^E\\ c^D\\ c^H\end{array}}_{,} \gamma =p/c^{\Psi }+\alpha , {\chi }_{ij}^{\Psi }=s_{ij}^{\Psi }/S_0.$

We have the matrix transfer function of the multilayer electromagnetoelastic actuator of adaptive optics for composite telescope and astrophysics equipment from the generalized structural-parametric model in the form

$\left[\Xi \left(p\right)\right]=\left[W\left(p\right)\right]\left[P\left(p\right)\right]$

where $\left[\Xi \left(p\right)\right]$ , $\left[W\left(p\right)\right]$ , $\left[P\left(p\right)\right]$  are the matrixes of the displacements the faces, the transfer functions, the control parameters.

In the static we obtained displacements for $t\to \infty$  the faces of the voltage-controlled multilayer piezoactuator for the longitudinal piezoeffect and the inertial load at $m<<M_1$ , $m<<M_2$ , where m is the mass of the multilayer piezoactuator, $M_1,M_2$  are the load masses, and the forces on faces $F_1\left(t\right)=F_2\left(t\right)=0,$  in the following form

${\xi }_1\left(\infty \right)=\underset{p\to 0}{\text{lim}}p{W}_{11}\left(p\right)\left(U/\delta \right)/p=d_{33}nU{M}_2/\left(M_1+M_2\right)$

${\xi }_2\left(\infty \right)=\underset{p\to 0}{\text{lim}}p{W}_{21}\left(p\right)\left(U/\delta \right)/p=d_{33}nU{M}_1/\left(M_1+M_2\right)$

${\xi }_1\left(\infty \right)+{\xi }_2\left(\infty \right)=d_{33}nU$

where U is the voltage.

For the multilayer piezoactuator at $d_{33}$ = 4∙10^-10 m/V, n=16, $U$ =100 V, $M_1$ =1 kg and $M_2$ =4 kg we obtained the static displacements of the faces the multilayer piezoactuator ${\xi }_1\left(\infty \right)$ =512 nm, ${\xi }_2\left(\infty \right)$ =128 nm, ${\xi }_1\left(\infty \right)+{\xi }_2\left(\infty \right)$ =640 nm.

We received transfer function of the multilayer piezoactuator at longitudinal piezoeffect with one fixed face and voltage control for the elastic-inertial load at $m<<M_2$  in the following form

$W\left(p\right)=\frac{{\Xi }_2\left(p\right)}{U\left(p\right)}=\frac{d_{33}n}{{\left(1+C_e/C_{33}^E\right)}_{}^{}\left(T_t^2{p}^2+2T_t{\xi }_{t}p+1\right)}$

$T_t=\sqrt{M_2/\left(C_e+C_{33}^E\right)}$ ,  ${\xi }_t=\alpha {\left(n\delta \right)}^2{C}_{33}^E/\left(3c^E\sqrt{M_2\left(C_e+C_{33}^E\right)}\right)$  

where ${\Xi }_2\left(p\right)$ , $U\left(p\right)$  are the Laplace transforms the displacement face and the voltage, $T_t$ , ${\xi }_t$  are the time constant and the damping coefficient, $C_{33}^E=S_0/\left(s_{33}^{E}n\delta \right)$  is the rigidity of the multilayer piezoactuator for $E=\text{const}$ .

At the elastic-inertial load for $d_{33}$ =4∙10^-10 m/V, n=12, U=200 V, $M_2$ =4 kg, $C_{33}^E$  = 2∙10⁷ N/m, $C_e$ =0.4∙10⁷ N/m we received the steady-state value of the displacement of the multilayer piezoactuator ${\text{ξ}}_2$ =800 nm and the time constant $T_t$ =0.4∙10^-3 s.

The structural-parametric model, structural diagram and the matrix transfer function of the multilayer electromagnetoelastic actuator of adaptive optics for composite telescope and astrophysics equipment are obtained. The static and dynamic characteristics of the multilayer actuator are received with using the matrix transfer function of the multilayer electromagnetoelastic actuator.

None.

The author declares there is no conflict of interest.

1. Schultz J, Ueda J, Asada H. Cellular Actuators. Butterworth-Heinemann Publisher, Oxford, 2017. p. 382.
2. Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady mathematics. 2006;74(3):943–948.
3. Zhou S, Yao Z. Design and optimization of a modal-independent linear ultrasonic motor. IEEE transaction on ultrasonics, ferroelectrics, and frequency control. 2014;61(3):535–546.
4. Przybylski J. Static and dynamic analysis of a flextensional transducer with an axial piezoelectric actuation. Engineering structures. 2015;84:140–151.
5. Uchino K. Piezoelectric actuator and ultrasonic motors. In: Boston MA editor. Kluwer Academic Publisher. 1997. p. 347.
6. Karpelson M, Wei G-Y, Wood RJ. Driving high voltage piezoelectric actuators in microrobotic applications. Sensors and Actuators A: Physical. 2012;176:78–89.
7. Afonin SM. Block diagrams of a multilayer piezoelectric motor for nano- and microdisplacements based on the transverse piezoeffect. Journal of computer and systems sciences international. 2015;54(3):424–439.
8. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transduser. Doklady physics. 2008;53(3):137–143.
9. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady mathematics. 2006;73(2):307–313.
10. Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London, 1946. p. 806.
11. Mason W. Physical Acoustics: Principles and Methods. Vol.1. Part A. Methods and Devices. Academic Press, New York, 1964. p. 515.
12. Zwillinger D. Handbook of Differential Equations. Academic Press, Boston, 1989. p. 673.
13. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. In: Parinov IA editor. Nova Science, New York, 2015. p. 225–242.
14. Afonin SM. A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. Chapter 8 in Advances in nanotechnology. Volume 19. In: Bartul Z et al., editors. Nova Science, New York, 2017. p. 259–284.
15. Afonin SM. Nano- and micro-scale piezomotors. Russian engineering research. 2012;32(7–8):519–522.
16. Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of solids. 2007;42(1):43–49.
17. Afonin SM. Stability of strain control systems of nano-and microdisplacement piezotransducers. Mechanics of solids. 2014;49(2):196–207.
18. Afonin SM. Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics. 2017;5(1):9–15.
19. Afonin SM. Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. International Journal of Physics. 2019;7(2):50–57.
20. Afonin SM. Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and microdisplacement. International Journal of Mathematical Analysis and Applications. 2016;3(4):31–38.
21. Afonin SM. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):1–9.
22. Afonin SM. Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics. 2018;2(2):52–59.
23. Afonin SM. Parametric block diagrams of a multi-layer piezoelectric transducer of nano- and microdisplacements under transverse piezoelectric effect. Mechanics of Solids. 2018;52(1):81–94.
24. Afonin SM. Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology. Proceedings of the 2018 IEEE Conference EIConRus. 2018. p. 1698–1701.
25. Afonin SM. Electromagnetoelastic nano- and microactuators for mechatronic systems. Russian Engineering Research. 2018;38(12):938–944.
26. Afonin SM. Structural-parametric model of electro elastic actuator for nanotechnology and biotechnology. Journal of Pharmacy and Pharmaceutics. 2018;5(1):8–12.
27. Afonin SM. Electromagnetoelastic actuator for nanomechanics. Global Journal of Research in Engineering. A: Mechanical and Mechanics Engineering. 2018;18(2):19–23.
28. Afonin SM. Structural–parametric model electroelastic actuator nano– and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecology and Environmental Sciences. 2018;3(5):306‒309.
29. Afonin SM. Static and dynamic characteristics of multilayered electromagnetoelastic transducer of nano- and micrometric movements. Journal of Computer and Systems Sciences International. 2010;49(1):73–85.
30. Afonin SM. Static and dynamic characteristics of a multi-layer electroelastic solid. Mechanics of Solids. 2009;44(6):935–950.
31. Afonin SM. Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1–14.
32. Bhushan B. Springer Handbook of Nanotechnology. Springer, Berlin, New York, 2004. p. 1222.