The characteristics of stationary, concentrated vortices of a special type are studying. The new solution for the problem of a concentrated vortex with three components of the velocity vector was constructed using a cylindrical coordinate system. Vortices of this type can be initiated by intense evaporation of moisture in a limited area of the water surface.

Keywords: concentrated vortices, coriolis effect, cylindrical coordinate system, velocity vector, three components, velocity distributions, pressure distributions

The mechanisms leading to the generation of various types of vortices are of great interest for meteorology and services that protect the population from natural disasters.^1–4 At present, a large number of tornadoes are observed annually in the United States and in many other countries. A cyclone (anticyclone), which is a giant atmospheric vortex with a low (high) pressure at the center and the presence of temperature and pressure gradients, can form from a small vortex in the atmosphere above the surface of lakes, mars, and oceans. It is known that cyclone development (anticyclone) consists of three stages: the initial stage, the quasistationary stage of existence, and decay.^1–4 It is at the quasistationary stage of vortexes existence various methods of investigations influence can be effective. The purpose of this work is to study in a cylindrical coordinate system the characteristics of stationary, concentrated vortices of a special type. The new solution for the problem of a concentrated vortex with three components of the velocity vector $\overrightarrow{u}=\left(u_r,u_{\phi },u_z\right)$ was constructed. Vortices of this type can be initiated by intense evaporation of moisture in a limited area $F=\pi R^2$ of the water surface.

Stationary, concentrated vortex with three velocity components that depend on the vertical and radial coordinates

For a detailed analysis of the distribution of velocities, pressures, and temperatures in a concentrated vortex of a special type for an inviscid medium with allowance for the Coriolis effect $2\left[\Omega k\times u\right],$  it is necessary to find a complete solution to the system of equations of continuity and motion:

$\nabla \cdot u=0, \frac{1}{\rho }\nabla \rho +\frac{u^2}{2}+2\left[{\Omega }_k\times u\right]-u\times \Omega =0$   (1)

Here, is the medium speed, $\Omega =\nabla \times u$  is the vortex.

Special cases of eddy currents in which the directions of the vorticity and velocity vectors are collinear belong to the class of Gromeka–Beltrami^8–11 and NЕ Zhukovsky currents.^12,13 In,⁸ it was shown that the velocity field can be found in a concentrated vortex when the condition.

$\left[\nabla \times u\right]\equiv \Omega = ku, \nabla \cdot u=0, k=const.$   (2)

Here, k is the unknown parameter in the process of problem solution

The concentrated vortex $\Omega r, z =\nabla \times u r,z =k . u r,z$  obtained in⁸ contained two velocity components that depend only on the radius. Of no less interest are concentrated vortices with three velocity components that depend not only on the radius but also on the vertical coordinate

$u=u r,z = u_r, r,z ,u_{\phi } r,z ,u_z r,z$   (3)

Given the Coriolis Effect, the system of equations of motion splits into the equation

$\nabla \times u r,z - 2{\Omega }_c=k . u r,z ,$

Which, unlike (2), is reduced to the system of equations for flow rates

$\{ -\frac{\partial u_{\phi }}{{\partial }_z}=k{u}_{r,}\frac{\partial u_r,}{{\partial }_z}-\frac{\partial uz}{\partial r}=k{u}_{\phi },\frac{1}{r}\frac{\partial r{u}_{\phi }}{\partial r}= k{u}_z + 2{\Omega }_k,$   (4)

And the equation to determine the pressure distribution in a vortex is

$\frac{p}{\rho }+\frac{u^2}{2}=\prod =const.$   (4a)

In addition to this system of equations, the velocity vector must satisfy the continuity equation written in a cylindrical coordinate system:

$\nabla \cdot u=\frac{1}{r}\frac{\partial }{{\partial }_r}r{u}_r+\frac{\partial }{{\partial }_z}{u}_z=0.$   (5)

Constant k in system (4) it is to be determined from the corresponding boundary conditions

The solution of system (4) must be sought with regard to the implementation of (5). The approach to this system with regard to (6) is that the continuity equation is solved identically, if we seek a solution in the form

$u_r=-\frac{\partial }{{\partial }_z}\Psi r,z , u_z=\frac{1}{r}\frac{\partial }{{\partial }_r}r\Psi r,z .$   (7)

From (7) and (4), it follows that the equation for the function $\Psi r,z$  is

$\frac{{\partial }^2\Psi }{\partial z^2}+\frac{\partial }{\partial r}\frac{1}{r}\frac{\partial r\Psi }{\partial r}+k^2\Psi =0.$   (8)

The solution of this elliptic equation can be found by the method of variable separation: Substituting the proposed form of the solution into the original equation (7), we get

$\{\begin{array}{l}S"+\frac{1}{r}S\text{'}+S k^2 -{\lambda }^2 -\frac{1}{r^2}=0\\ Z"=-{\lambda }^{2}Z.\end{array}$   (8)

In equations (8) arbitrary constants $\lambda k$ are determined from the boundary conditions of the problem. Further solution of the problem, which makes it possible to find the velocity distribution along the vortex radius and height, depends on the choice of specific boundary conditions.

Vortex with Radius R with a Stream Flowing into the Thickness Layer H.

The general solution of the second equation (8) is

$Z\left(z\right)=C_1 \exp \left(-i\lambda z\right)+C_2 \exp \left(i\lambda z\right)$   (9)

Constant $\lambda$ is found from boundary conditions that assume that the flow velocity is at a height H equal to zero:

$Z\left(z=0\right)=C\ne 0,$   (10)

$Z\left(z=H\right)=0.$   (11)

Given the first boundary condition (10), the solution for the function Z(z) has the form

$Z\left(z\right)=C \cos \left(\lambda z\right).$   (12)

Using the second boundary condition (11), we find

${\lambda }_n=\frac{\pi /2+\pi n}{H}, n=0,\mathrm{1....}\infty$   (13)

The first equation in (8) is a first-order Bessel differential equation; replacing the first equation in (26) is a first-order Bessel differential equation; replacing, we rewrite it as, we rewrite it as

$\frac{1}{r}\frac{\partial }{\partial r}\left[r\frac{\partial S}{\partial r}\right]+S\left(K^2-\frac{1}{r^2}\right)=0$   (14)

To solve (14), we use the boundary conditions for the function S(r)

$S\left(r_0\right)=0, \frac{d}{dr}S|{}_{r=0}=0,$   (15)

Taking into account (14), solution of the equation (14) can be written as an infinite sum of first-order Bessel functions

$S\left(r_0\right)={\displaystyle \sum _{j=1}^{\infty }{C}_j{J}_1}\left({\mu }_j^{\left(1\right)}\frac{r}{r_0}\right).$   (16)

Where ${\mu }_j^1$  are the zeros of the first-order Bessel function $J_1\left(K{r}_0\right)=J_1\left({\mu }_j^{\left(1\right)}\right)=0$

Substituting the solutions found for (12) and (16) into (8), for the azimuthal velocity component, we obtain (17)

$u\phi \left(r,z\right)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{j=1}^{\infty }{C}_{jn}{J}_1}\left({\mu }_j^{\left(1\right)}\frac{r}{R}\right)}\cos \left({\lambda }_{n}z\right).$   (17)

Knowing the values ${\mu }_j^1$ and ${\lambda }_n$ , we find $k_{jn}$

$k_{in}=\sqrt{{\left(\frac{{\mu }_j^{\left(1\right)}}{R}\right)}^2+{\left(\frac{\pi /2+\pi n}{H}\right)}^2, j=1,2,\mathrm{...}\infty , n=0,1,\mathrm{..}\infty .}$

The radial velocity is obtained from the first equation of system (4).

$u_r\left(r,z\right)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{j=1}^{\infty }{C}_{jn}\frac{{\lambda }_n}{k_{jn}}{J}_1}\left({\mu }_j^{\left(1\right)}\frac{r}{R}\right)}\sin \left({\lambda }_{n}z\right).$   (18)

Using from the third equation of system (4), the ratio

$\frac{\partial r{u}_{\phi }}{\partial r}={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{j=1}^{\infty }{C}_{jn}{\mu }_j^1\frac{r}{R}{J}_0 {\mu }_j^1\frac{r}{R} cos {\lambda }_{n}z}} ,$

we find the vertical component of the flow velocity in the vortex

$u_z\left(r,z\right)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{j=1}^{\infty }{C}_{jn}\frac{{\mu }_j^{\left(1\right)}}{k_{jn}R}{J}_0}\left({\mu }_j^{\left(1\right)}\frac{r}{R}\right)}\cos \left({\lambda }_{n}z\right)-\frac{2{\Omega }_k}{k_{jn}}.$   (19)

Vortices of this type can be initiated by intense evaporation of moisture in a limited area F of the water surface. So to find constants in the (19), we use equation

$2\pi {\displaystyle \underset{0}{\overset{R}{\int }}{\rho }_w{u}_z}\left(r,z=0\right)rdr=2\pi {\displaystyle \underset{0}{\overset{R}{\int }}{\rho }_w}\{{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{j=1}^{\infty }{C}_{jn}\frac{{\mu }_j^{\left(1\right)}}{k_{jn}R}{J}_0}\left({\mu }_j^{\left(1\right)}\frac{r}{R}\right)}-\frac{2{\Omega }_k}{k_{jn}}]rdr=G=const .$   (20)

Here ${\rho }_w$  is the density of moist air; G is the moisture evaporation rate.

To find the pressure distribution in the vortex, we use equation (4a), which implies $p\left(r,z\right)=\prod -\rho \frac{u^2}{0}.$ and using the condition

$r=R, p\left(r,z\right)=p_0\left(z\right),$   (21)

Here $p_0\left(z\right)$  is the atmospheric pressure varying with altitude/ To plot the graphs, we conduct the dimensioning:

$\tilde{u}=\frac{uk}{{\Omega }_k}=\tilde{\Omega }=\frac{\Omega }{{\Omega }_k}, \xi =\frac{r}{R}, \tilde{p}=\frac{p}{p_0}.$   (22)

Figure 1 shows the distribution of dimensionless velocities, vorticities along the vortex radius at $H=1000 { }_{\text{M}}.$  Figure 2 presents distribution of dimensionless pressure at altitudes $z=0.1 \left(1\right),0,5 \left(2\right),1 \left(3\right)$ .

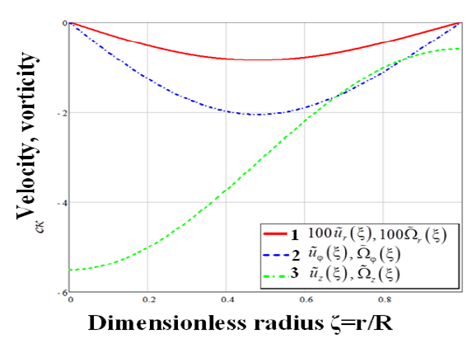
Figure 1 Distributions of the radial (1), angular (2) and vertical (3) components of velocity and vorticity at $\text{z =H/2 =}const.$

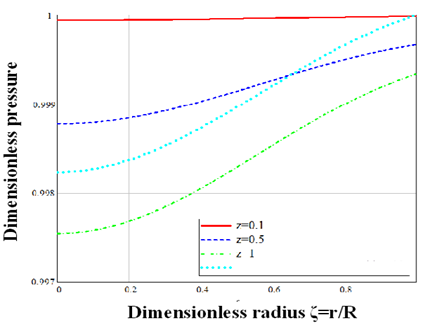
Figure 2 Distribution of dimensionless pressure at altitudes z = 0.1 (1), 0.5 (2), 1 (3) for a vortex with three velocity components and for a vortex with two velocity components (4).

Some applications obtained solutions can be found in the works.^14–16 We note again that the vortex intensity is directly proportional to the moisture evaporation rate. The solution obtained above can be used to create a series of vortices located in fixed areas, $F_j=\pi R_j^2, j=1,2,\mathrm{....},n$  of the horizontal surface of the water.

The new solution for the problem of a vortex with three components of the velocity vector $\overrightarrow{u}=\left(u_r,u_{\phi },u_z\right)$  that is concentrated a limited area $F_j=\pi R^2$  was constructed using a cylindrical coordinate system. Vortices of this type can be initiated by intense evaporation of moisture in a limited area F of the water surface.

None.

The author declares there is no conflict of interest.

1. Nalivkin DV. Uragany burii smerchi. Geograficheskie osobennosti i geologicheskaya deyatel’nost’ (Hurricanes, Storms, and Tornadoes: Geographical Features and Geological Activity). Leningrad: Nauka, 1969. p. 1–594.
2. Church C, Burgess D, Doswell C, et al. The Tornado: Its Structure, Dynamics, Prediction and Hazards. Geophysical Monograph Series Am Geophys. 1993;79:637.
3. Levens PJ, Labrosse N, Fletcher L, et al. Comparing UV/EUV line parameters and magnetic field in a quiescent prominence with tornadoes. Astron Astrophys. 2015;582:A27.
4. Doswell CA. Progress toward developing a practical societal response to severe convection (2005 EGU Sergei Soloviev Medal Lecture). Nat Hazards Earth Syst Sci. 2005;5:691–702.
5. Chefranov SG. Helicity generation in uniform helical flows. J Exp Theor Phys. 2004;99(5):987–997.
6. Gromeka IS. Sobranie sochinenii (Collected Works). Moscow: Akad. Nauk SSSR. 1952.
7. Sullivan RD. The Viscous Flow Near a Stagnation Point When the External Flow Has Uniform Vorticity. J Aerosp Sci. 1959;26:767.
8. Hide R. Helicity, superhelicity and weighted relative potential vorticity: Useful diagnostic pseudoscalars?. QJR Meteorol Soc. 2002;128:1759–1762.
9. Zhukovskii NE. O prisoedinennykh vikhryakh. Sobranie sochinenii (On the Attached Vortices: Collected Works). Moscow, 1949. p. 4.
10. Kochin NE, Kibel IA, Roze NV. Teoreticheskaya gidromekhanika (Theoretical Fluid Mechanics). In: Kibel IA editor. Moscow: Fizmatlit, 1963.
11. Sinkevich OA, Zinchenko GO. Complex Systems of Charged Particles and their Interaction with Electromagnetic Radiation. In Proc. 16th Int. Workshop, Moscow. 2018. p. 55.
12. Sinkevich OA. On the instability of the electrically charged interface between a two-phase thundercloud and turbulent atmosphere. High Temp. 2016;54(6):775–781.
13. Sinkevich OA. Exam Mar Biol Oceanogr. 2018;2(2).