In this article we review the potential of high spin-orbit coupling materials and their corresponding applications in spintronics. We look at an experimental result that demonstrated switching of perpendicular magnetic anisotropy by virtue of spin current generated from spin Hall material. This remains one of the most effective ways to generate high spin current density from charge current. Spin diffusion length at the interfaces remains a challenge, but surface engineering can produce very good quality bilayer structure that ensures spin penetration to the magnetic layer.

Keywords: spin-orbit, magnetic layer, electrons, cyclic motion, anisotropy

Spintronics have garnered lot of attention in recent times as an active replacement for transistors. Device engineers have come up with novel designs regarding the use of spin based magnetic memory. However, many of them still suffer from problems such as: high switching current density, low spin diffusion length etc. In this article, we are going to talk about a new design called spin-orbit torque magneto resistive random access memory (SOT-MRAM). This new design is a replacement for a previous design, spin transfer torque random access memory (RAM). This kind of structure can be used in field-free switching which can give rise to an entire generation of magnetic memory. This also holds promise form new magnetic field detectors, like the read heads used in hard drives. A major advantage of spin-orbit torque over spin transfer torque is the critical switching current. This can further be modified by optimizing the magnetic layer.

Spin-orbit torque uses spin-orbit coupling of a material, like heavy metal, to generate pure spin current from charge current. The magnetic field created by a moving electron with an angular momentum L, is given by:

$B= \frac{1}{me{c}^{2}r}\frac{\partial U}{\partial r}L$ (1)

Where U is the potential energy of the electron, mis the mass of the electron, eis the charge of the electron and cis the speed of light. This magnetic field then reacts with the magnetic moment of the electron to produce a shift in the energy of the electron. This change in Hamiltonian of the system is given by:

$\Delta H= \frac{{\mu }_B}{\hslash me{c}^{2}r}\frac{\partial U}{\partial r}L.S$ (2)

Where S is the spin angular momentum of the electron and ${\mu }_{{}_B}$  is the Bohr magneton. This shift in Hamiltonian includes Thomas interaction energy.¹ This is done by the virtue of spin Hall Effect. The generated spin current can then be used to switch the magnetization of a magnetic layer. The system tries to maintain a low energy for higher stability. Considering an electrostatic potential, the lowest energy will be the case when orbital and spin angular momentum are parallel to each other. This gives rise to a preferred direction of momentum with respect to spin. Hence, if spin 1/2 electron has a momentum p then the spin -1/2 electron will have momentum –p. This property is material dependent. Heavy metals, like Platinum, Tantalum, etc have demonstrated a spin Hall Effect. There has been a rise of new kind of materials called topological insulators (TI). The high spin-orbit coupling creates two distinct electronic states viz. Landau levels and edge states (Figure 1).²

Figure 1 Landau levels in the bulk and helical edge states along the surface.

Landau states are an extremely stable electronic state. They can be pictured by considering the cyclotron motion of an electron in a magnetic field. The energy of these levels is quantized and is given by:

$E=\left(n+\frac{1}{2}\right)\hslash {\omega }_c$ (3)

Where ${\omega }_c$ is the cyclotron frequency of the electron.³ However, if an electron is too close to the edge, the orbits are incomplete. The electron, upon hitting the edge undergoes elastic collision to bounce back into the sample. It tries to undergo another circular motion before hitting the edge another time to undergo the exact same result. In this way, it traverses along the edge in a helical structure. The electrons in edge states are mobile and hence conducting.⁴ This gives rise to a structure where the electrons close to the center are insulating and along the edges are conducting. Stacking the two dimensional (2D) sheets epitaxial gives rise to a three dimensional (3D) TI. In a 3D TI, the bulk consists of Landau levels making it insulating and the surface consists of edge states making it conducting.

These surface states are protected by time-reversal symmetry which cannot be broken.⁵ This means that the surface states are immune to physical alterations and strong disorders.⁶ This symmetry can be broken by an external magnetic field in which case, the material loses its TI properties. These surface states are a rich source of physics. The electrons in the surface states of a TI behave as a 2-dimensional electron gas (2DEG). 2DEG has been found in different heterostuctures such as: GaAlAs/GaAs structures.⁷ The important thing about the 2DEG is the extremely high mobility of charge carriers. This can increase massively at lower temperatures. The beauty of the TI surface states is that, the electrons are spin-momentum locked. Hence, the 2DEG on the surface of a TI gives rise to spin polarized electrons. Applying a transverse gate voltage, as the electron goes through the 2DEG, can control the spin of the electrons.⁷ The magnetic field produced from spin-orbit coupling can be modified to write:

$B=\frac{h}{m{c}^2}(E\text{x}k)$     (4)

Where Eis the electric field and kis the wave number of the electron. This magnetic field is perpendicular to both the electric field and the momentum of the electron. This magnetic field can apply a torque on the magnetic moment of the electron and manipulate the spin. This is further amplified by the fact that the magnetic field generated, is proportional to the momentum of the charge carriers. The momentum of charge carriers depend on a lot of factors including the crystal structure of the material which determines the effective mass of the carrier. However, 2DEG are known to have some of the highest mobility charge carriers. Hence, this can lead to an extremely high momentum which is then reflected in the magnetic field produced by the spin-orbit coupling. The control of spin polarized electrons form of the basis of Datta-Das transistor and future of logic devices beyond Moore’s law.⁸

At lower temperatures, the material can be treated as a disordered system. In such a system, the electron acts in a diffusive rather than ballistic manner. In a classical diffusive mode, the electron is treated by a random walk model:

$\langle r^2\rangle =Dt$ (5)

where $D$ is the diffusion constant. In such a model, the electron path is a Markovian chain, which implies that the future step of the electron only depends on the present state and is independent from any past step, making the process memory less. However, at smaller length scales, where quantum effects become prominent, this model breaks down. This can give rise to quantum interference of electron waves in cyclic scattering systems.^9,10 As an electron moves through a cyclic motion, the phase accumulated by it is: $\phi \alpha \oint \overrightarrow{p}.\overrightarrow{d}.$  This gives memory to the scattering process by distinguishing between the electrons that hop from other sites vs the electrons that underwent cyclic (clockwise and counter-clockwise) motion to reach the same place. By including the effects of quantum interference, we can do a rigorous derivation of the correction to conductance of the material. This correction leads to a net increased localization of electrons pertaining to increased probability for cyclic motion. This is referred to as weak localization. However, in the presence of spin-orbit coupling, the momentum and the spins are coupled together. A cyclic motion of the electron adds an extra phase of $\pi$  from the spinners. This leads a destructive interference and decreases the resistance. This can be seen in experiments with a strong cusp at the zero magnetic fields.

In a bilayer structure, we have magnetic layer on top of a spin Hall material. The Landau-Lifshitz-Gilbert-Slonczewski equation describes the magnetic precession under the effect of a magnetic field:

$\frac{dm}{dt}-\gamma m\text{ x }{H}_{eff}-\alpha m \text{x }\frac{dm}{dt}+\tau$    (6)

where 𝑚 is the unit vector along the direction of magnetization of the ferromagnetic layer, $\gamma =g{\mu }_{{}_B}/\hslash$ is the gyro magnetic ratio, where ${\mu }_{{}_B}$ is the Bohr magneton and is the Lande g-factor, $H_{eff}$ is the effective magnetic field determined by the external magnetic field as well as exchange stiffness, dipole field and anisotropy field, $\alpha$ is the Gilbert damping constant causing relaxation of magnetization to its equilibrium position, and $\tau$  denotes the current-induced torques.

The current-induced torqueses were derived by Slonczewski, using a semi-classical model of spin flow into magnetic layers. In general, this torque can be divided into 2 forms: field-like torque and anti-damping torque.¹¹ The anti-damping torque can be simplified and written in terms of spin current:

${\tau }_{{}_a}=-\frac{\gamma \hslash }{2e{M}_{s}V}m\text{ x }\left(m\text{ x }{I}_s\right)$    (7)

Where $M_s$ is the saturation magnetization and $V$ is the volume of the ferromagnet (FM). Spin current $I_s$ depends on the intrinsic spin Hall Effect (SHE) in TI. The field-like torque is given by:

${\tau }_f=-\frac{\gamma \hslash }{2e{M}_{s}V}{\beta }_s\left(m\text{ x }{I}_s\right)$ (8)

Where ${\beta }_s$  is the relative strength of field-like torque with respect to anti-damping torque. To a good approximation, the spin current can be considered proportional to the injected charge current: $I_s\propto pI$ where the proportionality constant $p$ depends on spin polarization and spin-orbit coupling of the TI.¹² Bilayers can lead to SOT based magnetization switching.¹³ Figure 2 shows a typical bilayer structure, taken from Zhao et al..¹⁴ Here, Ta plays the role of spin Hall material. When a charge current is passed through the Ta layer, spin current is generated in vertical direction. When the current pulse is sufficient to allow spin penetration into the magnetic layer (TbFeCo), the torque from spin polarized electrons switch the magnetization of the magnetic layer. The spin Hall torque is mostly generated from the anti-damping torque. The field-like torque is mostly negligible for many well known materials.

The anti-damping torque is directly proportional to the spin current and can be written as:

${\tau }_{\parallel }^0\frac{h}{2e{M}_{s^t}}\left|J_s\right|$    (9)

Figure 2 Schematic of SOT structure.¹⁴

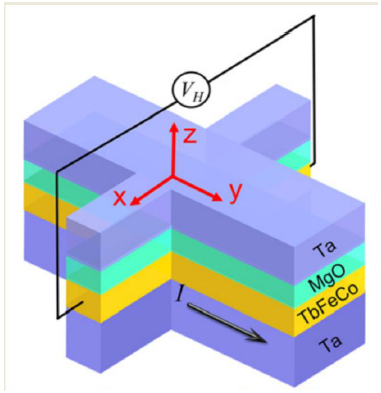
Hence, high current density can produce greater torque to switch the magnetization of the magnetic layer. The top MgO/Ta layer are the capping for protection from oxidation. A very valuable quantity for ractical applications is the ratio of generated spin polarized current to applied charge current in a SOC material. This quantity is called spin hall angle $({\theta }_{SH})$ . Many theoretical works have been done to find the critical current density for SOT switching of perpendicular magnetization.¹⁵

$J_c=\frac{2e}{h}\frac{M_s{t}_F}{{\theta }_{SH}}(\frac{H_{k,eff}}{2}-\frac{H_x}{\sqrt{2}})$   (10)

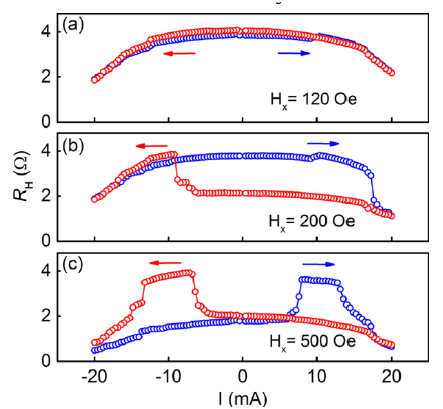
where $M_s$ is the saturation magnetization of the free layer, $t_F$  is the thickness of the free layer, ${\theta }_{SH}$ is the spin hall angle of the spin hall material, $H_{k,eff}$  is the effective anisotropy field and $H_x$  is the in-plane applied magnetic field. Hence, the magnetic layer and its properties can be modified to obtain a good charge current density needed. For most practical logic applications, the critical current density should be lower than 5 MA/cm2. The spin hall angle is temperature dependent. Most experimental evidences have shown a higher spin hall angle at lower temperatures. This is due to lower thermal collisions at lower temperature, which preserves the lifetime of the spin polarized current. Figure 3 Shows the variation of Hall signal with current at different transverse field. The transverse field in in-plane direction is necessary to break the symmetry. At around, 500 One of in-plane field we see a complete switching of magnetic layer. This switching of magnetic layer is by the virtue of torque applied by spin polarized current generated from the bottom Ta layer due to spin Hall Effect. Other bilayers have also demonstrated the potential for SOT switching. These can be combined with TIs to make very exotic spintronic devices.¹⁶

Figure 3 Hall resistance vs current at different transverse field.¹⁴

In summary, spin orbit torque based switching devices can be next possible revolution in spintronics. They are closest to make a possible RAM based on charge to spin current conversion. Material optimization is extremely important for these structures. Spin Hall material (heavy metals or TIs) are used to convert charge to spin current. Pulsed current can be used to generate high power spin current. This spin current, when penetrate, into the magnetic layer can generate a torque on the magnetic layer and switch the magnetization. Hybrid structures with anti- ferromagnet can be used to generate bias in-plane field, which is necessary for symmetry breaking. Switching of perpendicular magnetic anisotropy requires lower current density than in-plane anisotropy. Hence the rise of such devices can lead to novel memory devices such as SOT-MRAM, which combines the speed of solid state memory with non-volatility of magnetism. They can also be used for read head sensors in hard-disk drive. Gate-based devices with TIs can be the future for spin manipulation with electric field. These devices can open up gate ways for all spin logic devices. The very important advantage of spin based logic is the decreased power consumption with respect to charge based logic devices.