Electrochemical therapy is used for cancer and its application is simple, safe, effective and induces minimal adverse effects to the body. It is not accepted as one more oncospecific therapy, among other reasons due to its lack of standardization. Therefore, the scientific problem of this research is that an electrode arrangement is not defined that maximizes tissue damage in the tumor with minimal damage to surrounding healthy tissue that allows its optimization for therapeutic planning and personalized therapy. The objective of the study is to simulate and compare the spatial distributions of the electric potential, electric field, temperature and tissue damage and pH generated by multiple pairs of electrodes that maximize the destruction of the tumor volume. It is concluded that the results suggest that multi-pair electrode configurations may be more effective for the treatment of large (diameter> 8 cm) and deep solid tumors.

Keywords: electric potential, electric field, temperature, tissue damage, tumor.

The use of different types of physical anti-cancer therapies is gaining momentum in recent years, such as electroporation,¹ hyperthermia,² lasertherapy,³ electrochemical therapy (EChT)^4,5 and therapy E2 (EChT+ electroporation).^6-8 The EChT consists of the application of electric current very low intensity direct to the tumor by means of the insertion of two or more electrodes in its interior and/or vicinity. The application of this therapy is simple, safe, effective, and effective induces minimal adverse events. EChT is an additional option when therapies are not available. The specific onco-species fail or cannot be applied because of the depauperation of the general state of the cancer patient.⁹ In contrast, two studies show evidence of the death of several mice tumor carriers F3II under the action of the EChT.^10,11 The EChT has not been recognized as an additional oncospecific therapy because its mechanism of action is poorly understood, and doses and electrode arrangements have not been standardized. Physical-mathematical models are a quick and feasible way of understanding these three aspects.

In addition, its results do not require long lead times or substantial material resources, as the experiment. The Cuban Bioelectricity group focuses its efforts on proposing different models two-dimensional physical-mathematical (2D)^12,13 and three-dimensional (3D)^14,15 that allow us to know the spatial distributions of the electric potential (Ф), the intensity of the electric field (E), electric current density (J), the temperature (T), pH fronts generated by different geometries of multiple of individual electrodes^12-14 or pairs¹⁵ that are inserted collinearly or not in the tumor. The collinear and non-collinear insertions of the electrodes in the tumor are along and outside (at any place) of its major diameter, respectively. The se electrode configurations have been experimentally validated in tumors,^10,11,16 potato,^17,18 and in silico.¹⁸ Other electrode geometries have been used, in in vitro studies,^6,19 preclinical^5,20,21 and clinical.⁹

From theorical paint of view, the multiple pairs of non-collinear electrodes induce the higher values of PDT (more than 80%), with respect to the multiple individual electrodes inserted collinearly along the diameter of the tumor because the pairs of electrodes induce the highest values of the electric field and the temperature in the tumor. These results are remarkable when the pairs of electrodes are inserted at 45, 135, 225 and 315^o about the x-axis.¹⁵ This last arrangement of electrodes induces the highest values of the doubling time, percentage regression and retardation of carcinoma growthn mammary F3II highly aggressive and metastatic male and female BALB/c/Cenp mice. In addition, this type of electrode arrangement induces the highest survival of these mice for both genders. Despite this, complete remission of this variety histologic tumor damage is not observed in any mouse, and the overall antitumor effectiveness of the EChT induced by the pairs of electrodes arranged at 45, 135, 225 and 315^o is comparable to that of other electrode arrays used.¹⁰ The above mentioned in the previous paragraph may suggest that the geometry of multiple pairs of electrodes do not induce high values of tissue damage (simulations not shown),¹⁰ as the theory predicts.¹⁵ In contrast to these results, the complete remission of tumor F3II and high overall anti-tumor effectiveness of the EChT are documented when multiple individual electrodes are inserted along the major diameter of the tumor.¹¹ These aspects can be explained because these studies do not take into account the spatiotemporal behaviors of the because these studies do not take into account the space-time behaviors of the fronts of pH that are generated around the electrodes that are inserted into the tumor. Theoretical studies^13,18,22 and experimental^17,18-20,23 confirm that the acidic pH fronts  (pH ≤ 3) around the anodes and basic pH fronts (pH ≥ 12) around of the cathodes induce tissue damage.^15,22 Around the anode (positive electrode) is the documents the formation of hydrochloric acid, hydration of the tissue, detachment of chlorine and oxygen gases and induction of necrosis and apoptosis. Around the cathode (negative electrode) the formation of sodium hydroxide is reported, dehydration of the tissue, release of hydrogen gas and induction of necrosis.^17-23 pH fronts are extended in space and time during the application of EChT, when the distance between electrodes increases¹⁸ However, the effectiveness of this therapy decreases when this distance is greater than 3 cm and there is short-circuiting for one distance between electrodes less than 0.5 cm.²⁴ The electrode spacing of 3 cm is has been used in the experiment to reveal the different findings around the anode, cathode and in regions between and away from these electrodes.²⁰ The distance of 1 cm is the most widely used in preclinical studies^{10,11,16,19,21,23,24} and clinical,⁹ and potato.^17,18 However, the optimal distance between collinear electrodes is 0.7 cm.²⁵ Although the distance between individual electrodes has been addressed in the literature, the inter-pair distance of electrodes in multiple electrode pair geometries has not has been documented in the literature. It has also not been studied how the inter-pair distance of the affects the spatial distributions of Ф, E, T, fronts of pH acidic and basic. Therefore, the objective of this study is to simulate how the spatial distributions change Ф, E, T, acidic and basic pH fronts. Therefore, the objective of this study is to simulate how combine the spatial distributions of Ф, E, T, fronts of pH generated by multiple pairs of electrodes inserted into the tumor in terms of the inter-pair distance of electrodes.

The spatial pattern of tissue damage follows the electrode array geometry, but also the spatial profiles in terms of the electric potential, electric field/electric current density, and temperature according to computational simulations using 2D^13,19 and 3D^17,18,25 models. These computational results were supported using electrode arrays with other shapes in ECT.^21,22,24 In addition, González et al.⁹ and Suarez et al.²² showed that the spatial profiles of the electric field (obtained based on simulations) and tissue damage (experimental findings) follow the electrode array geometry. Thus, experimental and computational simulations suggest that the spatial patterns in terms of the physical magnitudes and tissue damage in 2D are similar to those on each side of a piece of 3D biological tissue when straight needle electrodes are inserted, as described in previous studies,^10,17 as shown in Figure 1.

Figure 1 Schematic representation of the spherical tumor a) and the arrays of a 45^o electrode pairs inserted into it b).

Model considerations

1. A heterogeneous region formed by a linear, heterogeneous, spherical solid tumor, heterogeneous and anisotropic of radius R (cm) of constant average electrical conductivity σ₁ (S/m) and constant average thermal conductivity κ₁ (W/cm °C), surrounded by the linear, heterogeneous, anisotropic healthy tissue of average electrical conductivity constant σ2 (S/m) and constant average thermal conductivity κ₂ (W/cm °C). The tumor-healthy tissue and healthy tissue-air interfaces were symbolized by Ʃ₁ and Ʃ₂, respectively (Figure 1a).
2. The mean scalar values of the tensors σ₁, σ₂, κ₁ and κ₂ (average values over tumor volume), as in previous studies.^{14,16,17,19 ,20}
3. Multiple straight needle platinum electrodes are inserted parallel to the z-axis, as assumed in^14,17 and used experimentally in.¹³
4. A potential difference (ΔVo) of 12 V is applied to the electrodes (+6 V for the anodes and -6 V for the cathodes), as in previous work.^10,17
5. A needle electrode consists of a straight wire of radius a, electrical conductivity much larger than σ₁ and insertion depth L in the tumor (part of the electrode at direct contact with the tumor), as in the experiment.^{10-13,22-24,27-30}

Calzado y cols¹⁴ simulated different geometries of multiple pairs of electrodes (electrode pairs of non-collinear electrodes and individual electrodes inserted collinearly along the diameter of the tumor). Of these geometries, the one that contains pairs of electrodes inserted at 45; 135; 225 and 315^o is the one used for the simulations in this study. This is argued because this electrode geometry induces the greatest decrease in the volume, growth retardation, regression percentage, and doubling time of the F3II mammary carcinoma growing in male and female BALB/c/C/Cenp mice, as well as the increased survival of mice (reported deaths associated with EChT.¹¹ The inter-pair distance of electrodes is d, the distance between pairs of electrodes is D, the positive polarity of electrodes 2; 4; 6 and 8, negative polarity of electrodes 1; 3; 5 and 7 are fixed in the experiment.¹¹ Therefore, the values of these parameters are used in the simulations in this study. The positioning of each electrode pair is referred to the x-axis (largest diameter of the tumor). The insertion depth length of the electrode in the the tumor is L and the radius of the tumor is R.¹⁴

Electric potential, electric field, and temperature spatial profiles

The options were used for the calculation of the F, E, T and heat transfer in solids. The Finite Element Method was used to obtain the numerical solution of the equations from F, E y T in a cubic domain. The Finer option was chosen for the meshing (volume of the 343.1 cm³ mesh). The simulation time was approximately 15 min for each mesh. Electrode configuration. The electrical potential in the tumor $({\Phi }_1)$ is the solution of the nonlinear Poisson equation because in this region we have completely inserted the electrodes. The electrical potential in the surrounding healthy tissue $({\Phi }_2)$ was the solution of the Laplace equation due to the non-existence of electrodes. The potentials ${\Phi }_1$ y ${\Phi }_2$ satisfy the border conditions ${\Phi }_1{|}_{\Sigma }={\Phi }_2{|}_{\Sigma }$ y ${\sigma }_1\partial {\Phi }_1/\partial \widehat{n}{|}_{\Sigma }={\sigma }_2\partial {\Phi }_2/\partial \widehat{n}{|}_{\Sigma }.$ In both tissues, E y T are calculated from $\overrightarrow{E_i}=-\nabla \text{Ф}$ (i = 1,2) and the stationary equation Pennes equation, respectively. The Pennes equation is given by

$\nabla \cdot \left(k_i\nabla T_i\right)-w_{b_i}{c}_{b_i}{\rho }_{b_i}\left(T_i-T_a\right)+q_i{}^{\cdots }+{\sigma }_i{\left|\nabla {\Phi }_i\right|}^2=0$   (i = 1,2)  (1)

where i = 1 represents the tumor and i = 2 the surrounding healthy tissue, T_a the arterial temperature and T_i the temperature induced in each medium. T₁ and T₂ satisfy the conditions of boundaries at the interface $\Sigma :T_1{|}_{\Sigma }=T_2{|}_{\Sigma }$ y ${\kappa }_1\partial T_1/\partial \widehat{n}{|}_{\Sigma }={\kappa }_2\partial T_2/\partial \widehat{n}{|}_{\Sigma }$ . The parameters κ_i, c_bi, ρ_bi, w_bi y q_i´´´ are the thermal conductivity of the fabric, the specific heat capacity the mass density of the blood, the rate of perfusion of the blood and the generation of heat of each tissue, respectively.^1,17,18

The Pennes bioheat equation was chosen because it is the most widely accepted equation for the calculation of the bioheat value,^17,18 ΔVo is constant, and transient variations of temperature that appear during the first moments of the application of EChT are disregarded with respect to the thermal effects induced in the tumor by the application of ΔVo. Variations in T_i (i = 1.2) due to nonlinearities are introduced in the coefficients σ_i (i = 1.2). In addition σ_i (i = 1.2) changes due to changes in the electrical properties of the tumor, because $E_i$ y $T_i$ (i = 1.2) are modified by the application of ΔVo. For the simulation of the geometry, meshing and solution, we used the commercial package of finite element software Comsol Multiphysics®4.3 (COMSOL AB Sweden, license number 2074929 FNL provided by the Electromagnetism Laboratory Computational, UNICAMP, Brazil). A Matlab-Comsol© interface was used for compatibility of the Comsol results with Matlab® R2015a (The MathWorks, Inc. USA). Once the data had been converted to Matlab® format, the following were calculated EEi; TTi; Eimax/Eimin y Timax/Timin. In addition, all the figures were made in Matlab® R2015a. For the simulations and calculations, we used a PC, Intel(R) Core(TM) i5-7200U a 2,50 GHz and 8192 Mbyte of RAM. In it a sphere was designed in Comsol Multiphysics®4.3. (representing the tumor), surrounded by a cube (representing the surrounding healthy tissue), as shown in the figure1 and 2. These two figures show the details of the insertion of the pairs of electrodes (represented as solid platinum cylinders and radius a) do not collinear, which is suggested for large and deep tumors,^13,17(Figure 1b).

Figure 2 Mesh created in the cubic heterogeneous domain for solving the equation of Poisson-Laplace and Pennes' stationary bioheat transfer equation in the tumor and surrounding healthy tissue.

The software automatically defines the size of each element of the geometry.¹⁴ The part of the electrode that is not in contact with the sphere is insulated with a plastic, as in the experiment (insulator is a plastic cannula).^{10-13, 23,24,27-31} The parameters of the geometry of the electrode array were: number of electrodes (C=8), inter-pair distance of electrodes(d = 1) cm, angle of each pair of electrodes with respect to the x-axis (θ = 45^o, 135^o, 225^o, 315^o), length of electrode insertion depth into the tumor (L=1,5) cm and the distance between pairs of electrodes in a pair (D = 0,5) cm. For the calculation and spatial distribution of E and pH fronts, the in silico EChT model was used. This model is mainly based on previously reported in.^13,18 We assumed that ion transport is solely governed by diffusion and migration, and electroneutrality holds true. Therefore, in silico 2D model can be described by the Nernst–Planck equations, for the concentration of ions in a four-component electrolyte (H+, OH−, Cl−, Na+) under galvanostatic conditions, and the underlying electrochemical reactions. Furthermore, the solution near anode is assumed saturated with respect to oxygen and chlorine, in an effective pressure of 1 atm at equilibrium with respect to the surface of anodic platinum electrode. The kinetics of electrodes are based on reaction mechanisms and kinetic parameters that are obtained from experimental measurements presented in.¹⁸ Changes in tissue permeabilization are also considered.

Model equations

$\frac{\partial C_A}{\partial t}=-\nabla \cdot N_A+R_A$   (2)

with the molar flux (mol/m² s) $N_A=-D_A\nabla C_A-\frac{z_A}{\left[z_{A]}\right]},u_A{C}_A\nabla$ , where C_A (mol/m³), D_A (m²/s), z_A y u_A (m²/V∙s) are the concentration, diffusion coefficient, charge number and mobility of the specie A, respectively z_A are signed quantities, being, positive for cations and negative for anions; t is the time in (s), R_A represents the production of the specie A throught chemical reactions in the electrolyte and Φ (V) is the electric potential. In this work we implemented the in silico model using a 2D-cartesian coordinate system. The space derivatives were ap-proximated by the finite difference method. An equally spaced mesh grid with 250 ×250 nodes was used. Distances between nodes and the time step were set to 10⁻⁴ m and 5 ×10⁻⁴ s, respectively. Each electrode was modeled as a point electrode. The outward unit normal vector from electrode boundary equations was selected, arbitrarily, under the left direction, allow-ing it simplify the equations system. For the six electrode configurations, the applied current density was 400 A/m² (applied current was 10 mA).¹⁶ The computational model was written in C ++ and implemented in an Intel ® Core (TM) i7 Proces-sor under Linux Ubuntu operating system. The non-linear equations system at anode and cathode were solved by method of Newton, using Multidimensional Root-Finding routines from the GNU Scientific Library (GSL).

Numerical simulations

Numerical simulations use the values of the following parameters a = 0,035 cm; R (2,5 cm); σ₁ = 0,4 S/m; σ₂ = 0,2 S/m;¹⁵ κ₁= 0,564 W/mK; κ₂ = 0,0022 W/cm^oC;³⁰ T_a = 37^oC; C_b1 = 3 840 Jkg^-1K^-1; C_b2 = 2,3 Jkg^-1oC^-1; ρ_b1 = 1 039 kgm^-3; ρ_b2 = 0,9 kgcm^-3; w_b1 = w_b2 = 0;00715 s^-1; y q₁ ´´´ = q₂ ´´´ = 10,437 Wm^-3.³⁰ It is important to note that (i = 1,2), are generally different in both tissues. The relative permittivities of the tumor, from healthy tissue and from each electrode were considered. Chemical, physical, mechanical and thermal parameters of the material platinum are implemented in the $A=\pi r^2$ softwear and the values of the parameters for the pH fronts were $C_{H+}^O={10}^{-4}mol/m^3$ ;²⁵ $C_{Na+}^O= 160mol/m^3$ ;²⁵ $C_{H_{2 }0}^O=55,500mol/m^3$ ; $P_{H^{+}}^0=9,{31.10}^{(-9)}{m}^2/s$ ; $P_{N{a}^{+}}^0=1,{3310}^{-9}{m}^2/s$ ; $I_1^{eq}=1\cdot {10}^{-6}/m^2$ ; $Z_{H+}=1$ ; $Z_{C{L}^{-}}=-1$ ; ${\text{E}}_1^{eq}=0,816V$ ;²³ $\text{F}=96,485,3A\cdot s/mol$ ; $K_{w,f}=1,{510}^8{m}^3/mol\cdot s$ ; $C_{O{H}^{-}}^o={10}^{-4}mol/m^3$ ;²⁵ $C_{C{L}^{-}}^o=160mol/m^3$ ;²⁵ $T=298K$ ; $P_{O{H}^{-}}^O=5,26\cdot {10}^{-9}{m}^2/s$ ; $P_{C{L}^{-}}^O=2,03\cdot {10}^{-9}{m}^2/s$ ; $I_2^{eq}=10A/m^2$ ;²⁴ $Z_{O{H}^{-}}=-1$ ; $Z_{N{a}^{+}}=1$ ; $E_2^{eq}=1407 V$ ;²³ $R=8,31kg\cdot m^2/k\cdot mol\cdot s^2$ ; $K_{w,b}=2,7\cdot {10}^{-5}{s}^{-1}$ .¹³

For the calculations, the units of meter and Kelvin were converted to centimeter and degree Celsius, respectively. In each simulation it was ensured that the metallic part of the electrode was in contact only with the tumor, and not with the surrounding healthy tissue (electrical insulation with a plastic cannula), as in the experiment.^10-13,30

In the tumor, the intensity of the maximum electric field was calculated, E_1max (V/cm); the minimum electric field, E_1min (V/cm); the maximum temperature, T_1max (°C); the minimum temperature, T_1min (°C). In the surrounding healthy tissue, the intensity of the maximum electric field was calculated, E_2max (V/cm); the maximum temperature, T_2max (°C). In addition, it was calculated EE₁ ( $E{E}_1\text{=}\sqrt{{\displaystyle \sum }_{k=1}^{m_1}{\left|{\underset{E}{\to }}_{1k}\right|}^2}$ : sum of the local electric field strength over all points in the tumor), EE₂ ($E{E}_2\text{ =}\sqrt{{\displaystyle \sum }_{k=1}^{m_2}{\left|{\underset{E}{\to }}_{2k}\right|}^2}$ : sum of the local electric field over all points in the surrounding healthy tissue region), TT₁ ($T{T}_1\text{= }\sqrt{{\displaystyle \sum }_{k=1}^{m_1}{\left|{\underset{T}{\to }}_{1k}\right|}^{2 }}$ : sum of the local temperature over all points in the tumor) and TT₂ ($T{T}_2\text{= }\sqrt{{\displaystyle \sum }_{k=1}^{m_2}{\left|{\underset{T}{\to }}_{2k}\right|}^2}$ : sum of local temperature over all points in the region of the surrounding healthy tissue). These variables were used to compare the overall effect of each configuration of electrodes, respectively EE_i it is given in V/cm and TT_i in °C for tumor (i = 1) and surrounding healthy tissue (i = 2). In both tissues, these magnitudes were calculated in different planes and their results were shown in three planes (z = 0. 1,25 and 2,1) cm for R = 2,5 cm. The calculation of EE₁, EE₂, TT₁ y TT₂ suggested in previous studies.¹⁸

Table 1 shows the maximum and minimum values of the electric field strength and temperature generated by electrode configurations C₄₅^o in the tumor and in the surrounding healthy tissue in the planes z = 0; 1,25 y 2,1 cm; at EE_1máx(EE_1mín) is the maximum and minimum electric field value in the tumor, TT_1máx(TT_1mín) of maximum and minimum temperature in the tumor, EE_2máx.^19-24

Figure 3 shows the spatial distributions of electric potential intensity, electric field and temperature for electrode configuration C₄₅^oin tumor and surrounding healthy tissue.

Figure 3 Spatial distributions of the electric potential intensity (a), the electric field (b), and temperature (c) for a radius of the tumor and the surrounding healthy tissue (R = 2,5 cm).

Figure 4 shows the spatial patterns of the pH fronts generated by the electrode configuration in the tumor and the surrounding healthy tissue.

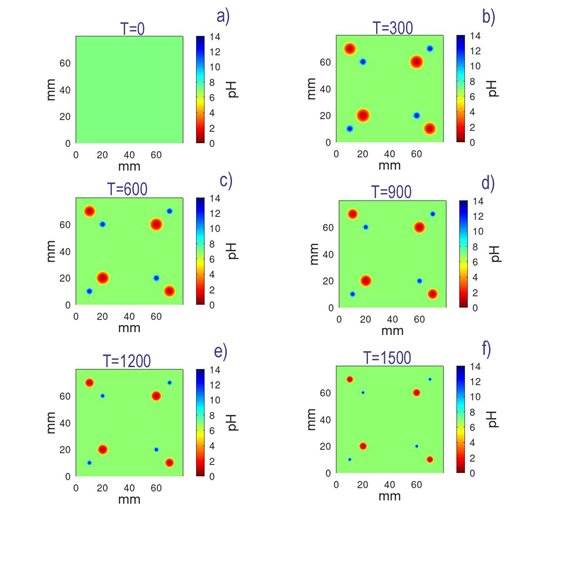
Figure 4 The spatial patterns of the pH fronts in the tumor and in the surrounding healthy tissue in order to T = 0 a), 300 b), 600 c), 900 d), 1200 e), 1500 f) s, respectively of application of the EChT.^11,22

Table 1 revealed that the higher values generated by the electrode configuration in the tumor of EE_1máx(EE_1mín) on (88,19(0,00) and 88,40(0,00) V/cm were observed for (z = 0 and 2,1 cm) and decreased at (z = 1,25 cm) and the values of TT_1máx(TT_1mín) on 74,52(37,54) and 60,18(37,48) °C increased for (z = 0 and z = 1,25) cm and decreased for (z = 2,1 cm) and in healthy tissue the highest values of EE_2máx de 50,18 (V/cm) were shown at (z = 2,1 cm) and the values of TT_2máx at 37,85 to 38,01 °C to (z = 1,25 and 2,1 cm), this is because this electrode configuration covers the entire tumor area and is effective for this type of therapy. Figure 3 revealed that F to E decreased with the inter-pair distance of the electrodes, between electrode pairs and in regions remote from the electrode pairs. The largest positive and negative values of F is observed around the anodes (red color) and cathodes (blue color), respectively which decrease along the Z-axis. The values of F and E are zeros in the surrounding healthy tissue. In contrast to the spatial patterns of F and T in every plane Z, la T is distributed non-uniformly throughout the tumor volumen. The highest values of T were observed around all anodes and cathodes and decreases for planes away from z = 0 cm. The values of T = 37 ^oC, T = (37 - 40) ^oC for z = (0 to 1,25) cm and T= (37,5 – 37)^oC for (z = 2,1) cm were observed in the surrounding healthy tissue. The values E_1max, E_1min, T_1max, T_1min are the maximum electric field, the minimum electric field, the maximum temperatura, the minimum temperature in each plane of the tumor (z = 0; 1,25 y 2,1 cm), respectively and E_2max to T_2max are the electric field, and the maximum temperature in the surrounding healthy tissue in these planes, respectively. Figure 4 showed that the pH fronts generated by the configuration C₄₅^o grew during the application of the EChT, being marked around the anode.^25,26,29,30 Although the results were not shown in this study, the simulations revealed that the results in table 1 and figures 3 and 4 were marked.  with increasing inter-pair distance of electrode. The results in this study confirm that the antitumor effect of the EChT is primarily around the anodes and cathodes that are consistent with those reported in.¹⁶ This fact corroborates that EChT can be applied indistinctly in electric current or voltage mode, as is done in the clinic, which suggests that the proposed configuration from simulations can be applied to the EchT in either voltage or current mode.

The spatial distributions of Ф, E, T and pH fronts generated by inserted electrode pair configurations in the tumor (C₄₅^o) adopt the geometry of the electrodes that are distributed throughout the tumor volumen, which is conducive to the greater anti-tumor effectiveness of the EChT.

None.

None.

1. Timmer F, Geboers B, Ruarus AH. Irreversible electroporation for locally advanced pancreatic cancer. Tech Vasc Interv Radio. 2020;23(2):100–675.
2. Skandalakis G, Rivera D, Rizea C. Hyperthermia treatment advances for brain tumors. Int JHyperthermia. 2020;37(2):3–19.
3. Densen, C. Cancer treatment using laser. U.S. Patent Application No 11/210,276, 4. 2021;11(2):906–924.
4. Miripour Z, Aghaee P, Mahdavi R. Nanoporous platinum needle for cancer tumor destruction by EChT and impedance–based intra–therapeutic monitoring. Nanoscale. 2020;12(43):22129–22139.
5. O’Brien C, Ignaszak A. Advances in the electrochemical treatment of cancers and tumors: exploring the current trends, advancements, and mechanisms of electrolytic tumor ablation. Chem Electro Chem. 2021;7(19):3895–3904.
6. Klein N, Mercadal B, Stehling M. In vitro study on the mechanisms of action of electrolytic electroporation (E2). Bioelectrochemistry. 2020;(133):107482.
7. Fujita S, Tamazawa M, Kuroda K. Effects of blood perfusion rate on the optimization of RF–capacitive hyperthermia. IEEE Trans Biomed Eng. 1998;45(9):1182–1186.
8. Garcia PA, Rossmeisl H, Neal RE, et al. A parametric study delineating irreversible electroporation from thermal damage based on a minimally invasive intracranial procedure. Biomed Eng Online. 2011;10(1):1–22.
9. Xin Y, Zhao H, Zhang W. Electrochemical Therapy of Tumors. Conference Papers in Science. 2013;(2013):13.
10. González MM, Morales DF, Cabrales LEB. Dose‐response study for the highly aggressive and metastatic primary F3II mammary carcinoma under direct current. Bioelectromagnetics. 2018;39(6): 460–475.
11. Goris NA, Rodríguez JLG, González M.M, et al. Efficacy of direct current generated by multiple–electrode arrays on F3II mammary carcinoma: experiment and mathematical modeling. Journal of Translational Medicine. 2020;(18):1–17.
12. Soba A. Integrated analysis of the potential, electric field, temperature, pH and tissue damage generated by different electrode arrays in a tumor under electrochemical treatment. Mathematics and Computers in Simulation. 2018;(146):60–176.
13. Calzado EM, Schincab H, Cabrales LEB, et al. Impact of permeabilization and pH effects in the electrochemical treatment of tumors. Experiments and simulations. Applied Mathematical Modelling. 2019;(74):62–72.
14. Calzado EM, Rodríguez JLG, Cabrales LEB, et al. Simulations of the electrostatic field, temperature, and tissue damage generated by multiple electrodes for electrochemical treatment. Applied Mathematical Modelling. 2019;(76):699–716.
15. Pupo AEB, Reyes JB, Cabrales LEB, et al. Analytical and numerical. Analytical and numerical a tumor tissue under electrotherapy. Biomed Eng Online. 2011;(10):85.
16. Pupo AEB, González MM, et al. 3d current density in tumors and surrounding healthy tissues generated by a system of straight electrode arrays. Mathematics and Computers in Simulation. 2017;(17):30011–30013.
17. Jiménez RP, Pupo AEB, Cabrales JMB, et al. 3D stationary electric current density into spherical tumor treated with low direct current. Bioelectromagnetics. 2011;(32): 120–130.
18. Cabrales LEB, Aguilera AR, Jiménez RP, et al. Mathematical modeling of tumor growth in mice following low–level direct electric current. Math Comput Simul. 2008;(78):112–120.
19. Li KH, Xin YL, Gu YN, et al. Effects of direct on dog liver: possible mechanisms for tumor electrochemical treatment. Bioelectromagnetics. 1997;(18):2–7.
20. Chou CK, Mc Dougall JA, Ahn Vora. Electrochemical treamente of mouse and rat fibrosarcomas with direct current. Biolectromagnetics. 1997;(18):18–24.
21. González MM, Aguilar CH, Pacheco FAD, et al. Tissue damage, temperature, and ph induced by different electrode arrays on potato pieces (Solanum tuberosum L.). Frontiers in oncology. 2018;(8):101.
22. Abrahamse H, Hamblin MR. New photosensitizers for photodynamic therapy. Biochem. 2016;(473):347–364.
23. Holandino C, Teixeira CAA, Oliveira FAG, et al. Direct electric current treatment modifies mitochondrial function and lipid body content in the A549 cancer cell line. Bioelectrochemistry. 2016;(111):83–92.
24. Mokhtare A, Reddy MSK, Roodan VA, et al. The role of pH fronts, chlorination and physicochemical reactions in tumor necrosis in the electrochemical treatment of tumors: A numerical study. Electrochimica Acta. 2019;(307):129–147.
25. Von Euler H, Olsson JM, Hutlenby K, et al. Animal Models for unresectable liver tumor: a histopathologic and ultra–structural study of cellular toxic changes after electrochemical treatment in rat and dog liver. Bioelectrochemistry. 2003;59(1–2):89–98.
26. Ren RL, Vora N, Yang F, et al. Variations of dose and electrode spacing for rat breast cancer electrochemical treatment. Bioelectromagnetics. 2001;22(3):205–211.
27. W John. Physiological Basis of Medical Practice. 1985;253(17):2587–2588.
28. W Moore. Basic Physical Chemistry. Physical Chemistry Chemical Physics. 1983;13(21):10048–10070.
29. Damjanovic A, Birss B. Electron transfer through thin anodic oxide films during the oxygen evolution reactions at Pt electrodes. Journal of The Electrochemical Society. 1991;138(9):2549.
30. Fuhrmann J, Guhlke C, Linke A. Models and numerical methods for electrolyte flows. Topics in Applied Analysis and Optimisation. 2019;39:183–209.