In the earlier article, the smallest physical constant was introduced and some new parameters were obtained to describe the elementary particles.¹ Based on these new parameters, we have further derived several equations to calculate a particle’s accelerations, the space curvature radius, and the force that space-time exerts to a particle. The minimum and maximum mass of a possibly existing particle can also be calculated. It is quite intriguing that these results can even be used to describe the cosmic evolution with time.

Keywords: parameters, space time, curvature, accelerations, cosmic evolution

Through many years of research, a new quantum constant k_o = 9.4868845×10^-60 erg×cm×s was discovered and introduced in the earlier article.¹ It is the smallest value of the product of space interval, time interval, and energy for all physical system. We call this the Space-Time Quantum of Action (STQA).

Because k_o is a very small constant, we can reasonably assume that the product of the space interval x, time interval τ, and energy E of all physical systems should be an integer multiple of k_o. This is the STQA Hypothesis. Its formula is $Ex\tau =n{k}_0$ then we can obtain the equation $E=E_0{n}^a, x=x_0{n}^b,\tau ={\tau }_0{n}^d$ and a + b + d = 1, where n is positive integer.  k₀=E₀x₀τ₀ we can then we calculated the value of a, b, d, and n for every elementary particle and the whole universe. We have demonstrated that 1/a, 1/b, and 1/d are the fractal dimension of energy, space, and time of a particle or a physical system.¹ Now we use the values of a, b, d, and n obtained in the earlier article to perform the following calculations.         

A diagram of parameters of particles

According to the table I in our article,¹ Fundamental parameters of particles based on the STQA hypothesis, every particle has a, b, d, and n values. If the abscissa stands for the logarithm of n, the ordinate stands for the values of a, b, and d of particles respectively, then a diagram can be drawn as Figure 1.

Figure 1 The relation between lgn and a, b, or d of particles.

According to this diagram, these equations can be found as follows:

For heavy particles, we have the equation (1):

$\begin{array}{l}a = 0.058 \lg n-2.115\\ b =-0.003 \lg n+1.099\\ d =-0.55 \lg n+2.016\end{array}$   (1)

For leptons we have the equation (2):

$\begin{array}{l}a = 0.012 \lg n-1.402\\ b =-0.003 \lg n+1.099\\ d =-0.009 \lg n+1.303\end{array}$   (2)

Based on equation (1), The inherent speed of heavy particles can be calculated using equation as shown in equation (3):

$\beta =n^{b-d}=n^{0.0521gn-0.917}\to \lg \beta =0.052{(\lg n)}^2-0.917\lg n$   (3)

The equation (3) indicated that there is a minimum value of the inherent speed that corresponding a particular particle’s state, it is shown in Figure 2. 

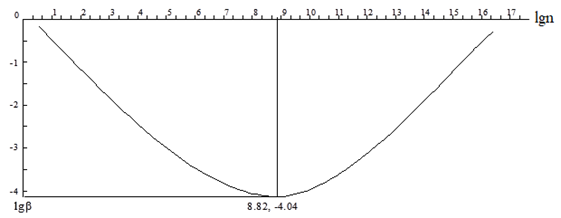
Figure 2 There is a minimum value of lgβ.

The minimum value can be calculated as shown in equation (4):

$\frac{d(\lg \beta )}{d(\lg n)}=0.104\lg n-0.917=0\to \lg n=8082\to {(\lg \beta )}_{\min }=-4.04$   (4)

That is the b_min=9´10^-5, this value corresponds to a particle that its mass is 2.4´10⁵GeV/c². 

Obviously, this could be the heaviest particle. Since this particle’s inherent speed is at a minimum, similar to the quarks (the quarks’ inherent speed is very little according to the table 1), so it is very difficult to detect the heaviest particle by experiment so far.

For the leptons, we can use equation (2) to get the particle that its inherent speed is maximum value, and its mass is lightest in all particles as shown as shown in equation (5):

$\lg n=33,{\beta }_{\max }=0.63,m=1.37\times {10}^{-5}eV/c^2$   (5)

The experiment suggests that neutrino have a mass of 0.1eV/c²,² which is greater than the mass of the lightest particle.

On the other hand, if we let a, b, and d can be represented by equations as shown in equation. (6) for all particles:

$a=\alpha \lg n+\varphi , b=\xi \lg n+\delta , d=\psi \lg n+\theta$   (6)

Whereare constants related to particles. We can deduce the equations that represent the inherent acceleration q, the inherent curvature radius of particles’ inherent motion r, and the inherent force that the space-time exerts to the particles F, as shown in equation (7), equation (8), and equation (9):

$q=q_0\frac{2(\xi -\psi )\lg n+(\delta -\theta )}{2\psi \lg n+\theta }{n}^{(\xi -2\psi )\lg n+(\delta -2\theta )}$   (7)

$\rho ={\rho }_0\frac{2\psi \lg n+\theta }{2(\xi -\psi )\lg n+\delta -\theta }{n}^{\xi \lg n+\delta }$   (8)

$F=F_0\frac{2(\xi -\psi )\lg n+\delta -\theta }{2\psi \lg n+\theta }{n}^{(\alpha +\xi -2\psi )\lg n+\varphi +\delta -2\theta }$   (9)

Where $q_0=c/{\tau }_0,{\rho }_0=x_0,F_0=E_0/c{\tau }_0.$

We can calculate the values of q,, and F of all kinds of particles using the three equations.  For example, for electron we have the equation (10):

$q=2.08\times {10}^{29}cm/s^2 , \rho =7.17\times {10}^{-12}cm , F=1.89 \times {10}^{2}dyne$   (10)

For proton we have the equation (11):

$q=1.19\times {10}^{35}cm/s^2 , \rho =1.67\times {10}^{-15}cm , F=1.99 \times {10}^{11}dyne$   (11)

For the heaviest particle we can get the equation (12):

$q=2.40\times {10}^{32}cm/s^2 , \rho =1.29\times {10}^{-19}cm , F=1.39 \times {10}^{13}dyne$   (12)

According to above calculations, the lighter particles correspond to larger curvature radius and smaller force between particles and space-time.  Thus, it is relatively easier to detect the particle that its mass between the heaviest and the lightest. In principle, we can calculate the inherent parameters of the motion of any system, such as atoms, molecules, the moon, the earth, the Galaxy, even the whole universe, as long as we known their values of n, .  Therefore, the parameters of the motion and space-time of every particle or physical systems depend on the inherent nature of them.

According to the equation (1) and equation (2), we can find that the formula to calculate the value of b are the same in both equations.  This implies the relation between the value of b and the value lg n has nothing to do with the type of particles.  Furthermore, we can think that formula to calculate the value of b fit to every physical system.  We can get the equation (13):

$\begin{array}{l}x=x_0{n}^b =x_0{n}^{-0.003\lg n=1.099}\to \lg x=\lg x_0+(-0.003\lg n+1.099)\lg n\\ \to \lg x=\lg x_0-0.003{(}^{\lg } +1.099\lg n\end{array}$   (13)

According to equation (13), the maximum of the space size x can be calculated by equation (14):

$\begin{array}{l}\frac{d(\lg x)}{b(\lg n)}=-0.003\times 2\lg n+1.099=0\to \lg n=183.2\to n=1.585\times {10}^{183}\\ \to b=-0.003\times 2\lg n+1.099=0.5494\to D_b=\frac{1}{b}=1.82\\ \to x_{\max }=x_0{n}^b=1.28\times {10}^{68}cm\to {\tau }_{\max }=\frac{x_{\max }}{c}=4.23\times {10}^{57}s\end{array}$   (14)

Let’s recall the n value of our current universe it is 8.06324×10¹⁸¹ that is almost the same as the n value in equation (14).  This means that the physical parameters of so small particles are closely related with the physical parameters of whole universe if this is not just a coincidence.  For whole universe, its value of n we take 1.585´10¹⁸³, and the value of n of whole universe should be a constant, let N = 1.585´10¹⁸³.  Therefore, based on the relationship between x and lg n, the maxima value of b can be obtained, it is 0.5494, and it is possible that there is a maximum size x_max = 1.28´10⁶⁸cm, and a maximum age t_max = 4.23´10⁵⁷ s for our universe.

Now let’s consider the start point of the universe, the big bang. The whole universe with total N = 1.585´10¹⁸³ STQAs, into the extreme small space time rang. There is a minimum size x₀ = 2.86´10^-33 cm, and a minimum time t₀ = 9.54´10^-44 s. let x = 2x₀, τ = 2τ₀, based on the STQA hypothesis, we have

$Ext=N{k}_0,E=E_0{N}^a,x=x_0{N}^b,\tau ={\tau }_0{N}^d$   (15)

We can obtain:

  a = 0.99661527, b = 1/607.9, d = 1/607.9, E = 10²⁰⁰ erg   (16)

 At this minimum value state, the value of b of whole universe is b = 1/607.9, this is the begin state of the big bang. 

Now, we have three group of values of b and τ, they are given by the current value b = 0.33347, t = 4.3512×10¹⁷ s, b and t in the equation (14), and b and t in the state of the big bang respectively.  According to the three group values of b and t, we can draw a quadric curve that represents the relation between lg b and lg t as shown in Figure 3.

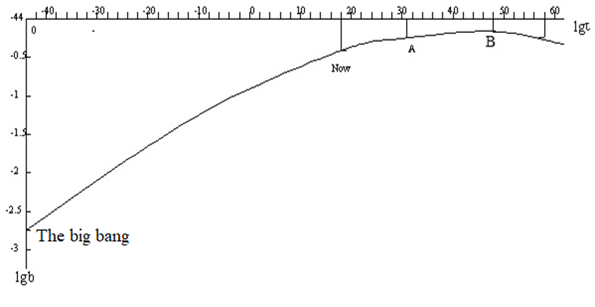
Figure 3 The time evolution of the universe.

The equation of the curve in Figure 3 can be shown in equation (17):

$Ext=N{k}_0,E=E_0{N}^a,x=x_0{N}^b,\tau ={\tau }_0{N}^d$   (17)

The maximum value of b or lg b can be calculated using equation (18):

$\begin{array}{l}\frac{d(\lg b)}{b(\lg \tau )}=-3.1794\times {10}^{-4}\times 2\lg \tau +2.9677\times {10}^{-2}=0\to \lg \tau =46.67\\ \to {(}_{\lg }=-0.2260\to b_{\max }=0.5945\to {(}_{D_b}=\frac{1}{b}=1.68\end{array}$   (18)

Based on Figure 3 and equation (18), we can see that the value of τ is about 10⁴⁷s, which corresponds to the maximum value of lg b. Therefore, the maximum age of the whole universe would be 10⁴⁷ s, which corresponds to a maxima size x _max = 3´10⁵⁷ cm. Currently, our universe’s size is x = 4.4×10²⁸ cm, the age is t = 4.3512×10¹⁷ s. Thus, our universe is expected to be expanding continuously.

If the final speed of the universe expansion reaches the limit, the speed of light, we expect that the speed of the universe expansion is getting faster and faster³ from the b < 1 to the ultimate b = 1 with its age greater and greater, it agrees with the results of observation.  Generally, every particle in the universe is accelerated from the speed of zero to the speed of light during 10⁴⁷s, therefore, the average acceleration of the universe expansion can be calculated to be about 10^-37cm/s², which waits for examination by the observation. 

According to the Figure 3, the value of b is increasing, or the space dimension D_b of whole universe is decreasing gradually with the passage of time.  Currently, the space dimension of universe is three, and it expects to decrease to two at the age of 10³¹ second, which corresponds to the point A on the curve.  Then it can decrease to 1.86 at the age of 10⁴⁷ second, which corresponds to the point B on the curve.  The quadratic curve takes point B as the symmetric point, and the left and right are symmetrical, and repeats the opposite evolution process after point B. 

Since these parameters can be calculated using the STQA theory, this pattern of evolution of the whole universe has nothing to do with the cosmological constant and the mass density of the universe.  Thus, the STQA theory suggests a novel concept and method to resolve the important problem related to the structure of the matter and the evolution of the universe.  It has been quite difficult to resolve these problems using existing physical theory as we know.

According to the equation (17), the value of b of the whole universe is changing slowly with the passage of time.  The reciprocal of b is the fractal dimension of space, thus, the fractal dimension of the space of the universe is decreasing gradually.  Because the nature of self-similar of the fractal set, then the void / hole of space-time in every size scale will be created with the space dimension of the universe become less than three gradually.  Based on the STQA theory, it could possibly produce an important influence on the living being that we have never been imagined before.

Based on the STQA theory, we can calculate the mass of the lightest and heaviest of particles, which are 1.37´10^-5 eV/c² and 2.4´10⁵ GeV/c², respectively. The particle’s accelerations, the space curvature radius, and the force that curved space-time exert to a particle can be calculated. Those results are waiting for the validation of experiments.

The STQA theory suggests a novel concept and method to resolve the important problem related to the structure of matter and the evolution of universe.  The dimension of the universe is changing as the time goes on, and its range of variation is from 607.9 to 1.86 with the current dimension at 3.  The maximum size for the universe expansion is 10⁵⁷ cm, and it corresponds to the age of the universe of 10⁴⁷ second.  At the same time, the average acceleration of the universe expansion can be calculated as 10^-37cm/s², which could be validated by experimental observation in the near future.  Thus, the STQA theory might lead to significant scientific advancement.

None.

None.

1. Shuming L, Lihua LH, Shuwei L, et al. The smallest constant of physics. Phys Astron Int J. 2023;7(2):99‒102.
2. Wolfenstein L, Physics World, 1998;17.
3. Amir DA, God’s Equation, Four Wall Eight Windows, New York,1999.