In equilibrium, coordinates of atoms in a molecule are expressed with respect to the origin situated at the center–of–mass of the molecule. In the quantum mechanical software MOLPRO, we have found that the center–of–mass of molecule does not coincide with the origin of the coordinate system. Rather it lies in a random manner. The problem becomes more severe when, for example, one wants to know the separation between two interacting particles in the scattering process. There appears need to make amendment in MOLPRO, so that the origin of coordinate system coincides with the center–of–mass of the molecule in equilibrium.

Keywords: ISM: molecules, interaction potential, MOLPRO

For quantum mechanical calculations of atomic systems, some software, e.g., Frischet et al.¹, Werner et al.² & Valiey et al.³ etc. are in use in science. For scattering between a molecule of interest and a colliding partner (generally taken as H₂ molecule for interstellar medium), a common procedure is to calculate the interaction potential between them. For convenience, the H₂ molecule is taken as structure–less particle and is often replaced by He atom, as both of them have 2 electrons and 2 protons.^4–15 In the process, the molecule is first optimized and the cartesian coordinates (x_i, y_i, z_i) of the atoms of molecule in equilibrium are obtained. The Cartesian coordinates (x_cm, y_cm, z_cm) of the center–of–mass of the molecule are expressed as

$x_{cm}=\frac{\sum m_i{x}_i}{ \sum m_i},y_{cm}=\frac{\sum m_i{y}_i}{\sum m_i},z_{cm}=\frac{\sum m_i{z}_i }{\sum m_i}$

where$m_i$ denotes the mass of the i–th atom. The origin of coordinate system is generally taken at the center–of–mass of the molecule, so that x_cm=0, y_cm=0, z_cm=0.

For a clear presentation, in the present discussion, we have taken the case of the interaction between H₂CS (thioformaldehyde) and He atom. The H₂CS is a planar molecule (say, lying in the yz–plane) as shown in Figure 1 and following the symmetries, the coordinates of its atoms in equilibrium may be expressed as given in Table 1. For coincidence of center–of–mass with the origin of coordinate system, we get the relation

$2m_H{z}_1+m_C{z}_2=m_S{z}_3$

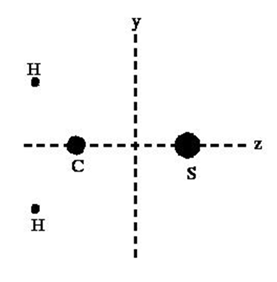
Figure 1 Geometry of the H₂CS molecule in equilibrium.

where$m_H$ ,$m_C$ and$m_S$ are atomic masses of hydrogen, carbon and sulpher, respectively. The positions of atoms of H₂CS are now kept fix. For calculation of interaction potential between H₂CS and He atom, one can put He atom at a point expressed in polar coordinates ($r,\theta ,\phi$ ) as shown in Figure 2. The Cartesian coordinates (xʹ, yʹ, zʹ) of He atom are

$x\text{'}=rsin\theta cos\phi ,y\text{'}=rsin\theta sin\phi ,z\text{'}=rcos\theta$

For interaction between H₂CS and He atom, the coordinates are given in Table 2. Then, the energies are calculated as:

1. Energy E₁($r,\theta ,\phi$ ) of H₂CS + He.
2. Energy E₂($r,\theta ,\phi$ ) of H₂CS while He atom is present as a ghost atom.
3. Energy E₃($r,\theta ,\phi$ ) of He atom while all atoms of H₂CS are present as ghost atoms.

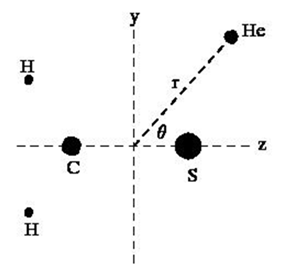
Figure 2 Interaction between H₂CS and He atom.

Here, the concept of ghost atom is introduced in order to consider the Basis Set Su–perposition Error (BSSE).¹⁶ The interaction potential V($r,\theta ,\phi$ ) between H₂CS and He atom is

$V\left(r,\theta ,\phi \right)=E_2\left(r,\theta ,\phi \right)+E_3\left(r,\theta ,\phi \right)-E_1\left(r,\theta ,\phi \right)$

The interaction potential V($r,\theta ,\phi$ ) is calculated for various positions of He atom and is used as input in the computer code MOLSCAT^17,18 to calculate the scattering cross sections for collisional transitions between rotational levels, as a function of energy of colliding partner. These cross sections are averaged over the Maxwellian distribution to get the scattering rate coeffcients, as a function of kinetic temperature in the medium.^12–15

We have found that on optimization of H₂CS with MOLPRO, the center–of–mass does not coincide with the origin of coordinate system. On inclusion of He atom, we do not know if the origin of polar coordinates ($r,\theta ,\phi$ ) (expressing the position of He atom) is at the center–of–mass of H₂CS, or at the origin defined in the MOLPRO, or somewhere else. Under such circumstances, it is difficult to have information about relative separation between the H₂CS molecule and He atom, which is essentially required.

On 01 April 2014, we have optimized the H₂CS with MOLPRO (Version 2012.1, Copyright, University College Cardiff Consultants Limited, 2008) by using the method CCSD (T) and basis set cc–pVDZ. The coordinates of atoms obtained are given in Table 3, which provide the center–of–mass at

$x_{cm}=0.00,y_{cm}=0.00,z_{cm}=0.1612625506$  (1)

On 21 September 2017, we have again optimized the H₂CS with MOLPRO (Version 2015.1, Copyright, TTI GmbH Stuttgart, 2015) by using the same method CCSD(T) and the same basis set cc–pVDZ. The coordinates of atoms obtained are given in Table 4, which provide the center–of–mass at

$x_{cm}=0.00,y_{cm}=0.00,z_{cm}=0.4667993088$ (2)

It shows the shifting of the center–of–mass without any reason.

The comparison of y–coordinates in Tables 3 & 4 shows that either the values are changed or the accuracy of data is up to the 4^th or 5^th decimal place. The comparison of z–coordinates shows a large variation in the values. In equations (1) and (2): (i) The value x_cm=0.00 is not surprising, as the H₂CS lies in the yz–plane. (ii) The two H atoms lie symmetrically opposite on the two sides of z–axis and therefore the value y_cm=0.00, as per expectation. (iii) Non–zero value of z_cm is surprising, as the center–of–mass of a molecule (in equilibrium) is generally taken at the origin of coordinate system. Two different values for z_cm may be interpreted that the center–of–mass is placed in a random manner in the MOLPRO. There is difference of 0.305536758 Bohr between the positions of center–of–mass when the H2CS is optimized with the help of MOLPRO on two different dates (01 April 2014 and 21 September 2017). It should not be the case. One may say that the molecule is shifted along the z–axis. But, the problem appears to know about the separation between H₂CS and He atom while calculating interaction between them.

This problem was submitted for consideration of the organizers of MOLPRO as well as the MOLPRO users, but no solution emerged out. None of them could tell how to get separation between the H₂CS molecule and He atom.

We have also optimized the Glycolaldehyde (C₂H₄O₂) with the help of MOLPRO. The coordinates obtained are given in Table 5. This is case of three–dimensional molecule. These coordinates provide the center–of–mass at

$x_{cm}=0.089435584,y_{cm}=-0.033493791,z_{cm}=0.000006947$     (3)

It also shows that the center–of–mass of Glycolaldehyde does not coincide with the origin of coordinate system. We have optimized other molecules also with the help of MOLPRO and similar situation of non–coincidence of center–of–mass of molecule and the origin of coordinate system is found.

In equilibrium, the center–of–mass of a molecule should coincide with the origin of coordinate system. We have found that for the considered molecules, it is not the case. The problem is found to become more severe, for example, when one wants to know the separation between the two colliding partner for scattering process. There appears need to make amendment in MOLPRO, so that the origin of coordinate system coincides with the center–of–mass of a molecule in equilibrium.

We are grateful to Hon’ble Dr. Ashok K. Chauhan, Founder President, Hon’ble Dr. Atul Chauhan, Chancellor and Prof.(Dr.) Balvinder Shukla, Vice–Chancelllor, Amity University for valuable support and encouragement. MKS is thankful to the SERB, DST, New Delhi for award of National Postdoctoral Fellowship.

Author declares there is no conflict of interest.

1. Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian Inc. 2010.
2. Werner HJ, Knowles PJ. MOLPRO ab initio program. 2008, 2015.
3. Valiey M, Bylaska EJ, Govind N, et al. NWChem: a comprehensive and scalable open–source solution for large scale molecular simulations. Computer Physics Communications. 2010;181(9):1477–1489.
4. Green S. Collisional excitation of interstellar molecules–Water. Astrophysical Journal Supplement Series.1980;42:103–141.
5. Machin L, Roueff E. Collisional excitation of monodeuterated ammonia NH2D by helium. Astronomy & Astrophysics. 2006; 460(3):953–958.
6. Machin L, Roueff E. Collisional excitation of doubly deuterated ammonia ND2H by helium. Astronomy & Astrophysics. 2007;465(2):647–650.
7. Wernli M, Wiesenfeld L, Faure A, et al. Rotational excitation of HC3N by H2 and He at low temperatures. Astronomy & Astrophysics. 2007;464(3):1147–1154.
8. Wernli M, Wiesenfeld L, Faure A, et al. Rotational excitation of HC3N by H2 and He at low temperatures. Astronomy & Astrophysics. 2007;475(1):391.
9. Dumouchel F, Faure A, Lique F. The rotational excitation of HCN and HNC by He: temperature dependence of the collisional rate coefficients. Monthly Notices of the Royal Astronomical Society. 2010;406(4):2488–2492.
10. Sarrasin E, Abdallah DB, Wernli M, et al. The rotational excitation of HCN and HNC by He: new insights on the HCN/HNC abundance ratio in molecular clouds. Monthly Notices of the Royal Astronomical Society. 2010;404(1):518–526.
11. Gotoum N, Nkem C, Hammami K, et al. Rotational excitation of aluminium monofluoride (AlF) by He atom at low temperature. Astrophysics and Space Science. 2011;332(1):209–217.
12. Sharma M, Sharma MK, Chandra S, et al. Collisional rates for rotational transitions in H2CO and their application. Advances in Space Research. 2014;54(2);252–260.
13. Sharma MK, Sharma M, Chandra S, et al. Collisional excitation of vinylidene (H2CC). Advances in Space Research. 2014;54(9):1963–1971.
14. Sharma MK, Sharma M, Chandra S, et al. Radiative transfer in silylidene molecule. Serbian Astronomical Journal. 2014;188:37–44.
15. Sharma MK, Sharma M, Chandra S, et al. Collisional excitation of thioformaldehyde and of Silylidene. Advances in Space Research. 2015;55(1):434–439.
16. Senent ML, Wilson S. Intramolecular basis set superposition errors. International Journal of Quantum Chemistry. 2001;82(6):282–292.
17. Hutson JM, Green S. MOLSCAT Computer CODE. UK: Version 14 Dis–tributed by Collaborative Computational Project No. 6 of the Engnieering and Physical Sciences Research Council; 1994.
18. Sharma MK, Sharma M, Chandra S. Some observations about the MOLSCAT. Communications in Theoretical Physics. 2015; 64(6);731–734.