Historically the observational evidence for the existence of Dark Matter came only from galactic dynamics and is gravitational. The following discussions in this section show that the observed luminous objects (stars, gas clouds, globular clusters, or even entire galaxies) can not have enough mass to support the observed gravitational effects .¹

Ceaseless efforts are being made for the last three decades towards revealing the mysteries regarding the nature of dark matter. A number of theoretical models have been proposed. On the basis of these models, experiments to search for dark matter and its nature are being planned and designed. Results of ongoing experiments are being analyzed and it is being constantly attempted to answer the question as what is the nature of dark matter. In the present chapter, it is attempted to review the developments in the search for dark matter.

Keywords: dark matter, gravitational waves

The question as to how this universe came into being and as to how it has evolved to its present stage, is an old question. The answer to this question unfolds many secrets regarding fundamental particles and forces between them. The most significant ingredient of this whole creation namely ‘Dark Matter’ was for the first time identified by Fritz Zwicky of California Institute of Technology (Caltech) in 1933. He studied Coma cluster of galaxies and found that the gravity of visible galaxies in the cluster would be far too small for such fast orbits. He inferred that there must be some non-visible form of matter which would provide enough of the mass and gravity to hold the cluster together. Decades of investigation confirmed his analysis.

In the present paper a detailed review on the evidences which are proving the existence of dark matter is presented. The recent development in the field of search of dark matter is also discussed with light on future challenges for the experimental search.

Clusters of galaxies

The clusters of galaxies are very large objects in the known universe. These have many properties which make them great astrophysical laboratories; clusters change extremely slowly and therefore may retain the scenario of the time when they were formed. This makes them suitable for the study history of structure and galaxy formation. Clusters tend to hold onto the gas in their systems, unlike galaxies, where the gas is forced out through supernova explosions. In other words, clusters are closed systems. By studying the chemical composition of clusters, it is possible to get a history of nucleosynthesis in the Universe. The force of gravity that holds clusters together comes mostly from dark matter, making clusters suitable to study dark matter in the Universe.² Virgo, Coma, Hercules and Norma are names of some main clusters in our universe. In recent work the evidences of existence of dark matter in clusters of galaxies were reinvestigated and some positive and perplexed results are obtained by various workers.^3–4

Rotation curves of spiral galaxies

The most convincing evidence for the existence of Dark Matter came from the measurement of the rotation curves of spiral galaxies in the 1970s by V. C. Rubin⁹ and other astronomers.^5-9 SPIRAL GALAXIES are flat rotating systems. The stars and gas in the disk are moving in nearly circular orbits, with the gravitational field of the galaxy providing the inward acceleration required for the circular motion. According to Newton’s Second Law, the rotational velocity v of an object on a stable orbit with radius r from the centre of galaxy is obtained by:

$\frac{v^2(r)}{r}=\frac{G_{N}M(r)}{r^2}$                                                 (1)

Namely

$v(r)\alpha \sqrt{\frac{M(r)}{r}}$                                         (2)

Where M(r) is the mass inside the orbit. For an object outside the visible part of the galaxy, one would that

$v\left(r\right)\alpha \frac{1}{\sqrt{r}}$                                                     (3)

At the beginning of the 1930s, F. Zwicky and other astronomers measured the total mass of a few clusters of galaxies and the masses of the luminous objects in these clusters of galaxies.^10-11 Their measurements showed that the masses of these clusters of galaxies required to gravitationally bind their galaxies are much larger than the sum of the luminous masses of their individual galaxies.

The rotation curve of a galaxy is represented by a graph that plots the orbital velocity of the stars or gas in the galaxy on the y-axis against the distance from the center of the galaxy on the x-axis. Stars revolve around the centre of galaxies at a constant speed over a large range of distances from the center of the galaxy. Thus they revolve much faster than would be expected if they were in a free Newtonian potential. After the advent of Radio telescopes, the rotation curves of spiral galaxies were very accurately obtained for regions beyond luminous inner regions. K.G.Begeman et al.¹⁰ obtained rotation curves for some simple spiral galaxies such as NGC 2403, NGC 2841, NGC 2903, NGC 3198, NGC 6503, NGC 7331. In Figure 1 these rotation curves obtained by K.G.Begeman are shown.¹²

Figure 1 Rotation curves for some simple spiral galaxies. The rotation curves of the individual components: visible component, gas, and dark halo, are also shown.¹²

However, measurements of the circular velocities of clouds of neutral hydrogen in galaxies by using their 21-cm emission showed that the rotation curves of spiral galaxies are flat (see Figure 1) or even rising at distances far away from their stellar and gaseous components.^7-13 This implies the existence of a “dark halo” around the galaxy with a total mass profile.¹⁴

$M(r)\alpha r$                                                                        (4)

i.e., the profile of the mass density should be

$\rho (r)\alpha \frac{1}{r^2}$                                                                       (5)

Since

$M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}{r}^2}\rho (r)dr$                                (6)

Escape velocity from the Milky Way

Escape velocity is the speed where the kinetic energy of an object is equal to the magnitude of its gravitational potential energy. The escape velocity from the Milky Way at the position of our Solar system has been estimated as¹⁵

$\nu {}_{esc}{}^{Galaxy}\ge 450km/s$                                  (7)

It is much larger than can be accounted for by the luminous matter in our Galaxy. It is not difficult to understand why this result is so surprising if one thinks about the huge difference between the escape velocity from the Sun’s surface which is 617.5km/s and for solar system at position of earth its value is 42.1km/s.^1–15 Recall that the gravitational well in our Solar system is caused by the Sun’s mass which dominates the total mass of the Solar system. If the mass of the luminous matter in our Galaxy would also dominate the total mass of the Galaxy, the escape velocity from our Galaxy at the position of our Solar system would then be reduced by one order of magnitude.

Cosmological density parameters

The cosmological constant, conventionally denoted by the Greek letter Λ, is a parameter describing the energy density of the vacuum (empty space), and without a potentially important contributor to the dynamical history of the universe. Unlike ordinary matter, which can clump together or disperse as it evolves, the energy density in a cosmological constant is a property of space time itself, and under ordinary circumstances is the same everywhere. Sufficiently large cosmological constant Λ will cause galaxies to appear to accelerate away from us, in contrast to the tendency of ordinary forms of energy to slow down the recession of distant objects. The cosmological density parameter of a given component of the total energy of the Universe Ω_i has been defined as the density of this component averaged over the Universe, ρ_i, in units of the critical energy density of the Universe, ρ_crit,

${\Omega }_i=\frac{{\rho }_i}{{\rho }_{crit}}$                                                                              (8)

The critical energy density of the Universe is the value that makes the geometry of the Universe flat.^16,17

${\rho }_{crit}=\frac{3H_0^2}{8\pi G_N}\approx 2.775\times {10}^{11}{h}^2{M}_{\Theta }/Mp{c}^3$

$\approx 1.878\times {10}^{-20}{h}^{2}g/c{m}^3$                      (9)

and H₀ denotes the expansion rate of the Universe its present value is 100h km/s/Mpc.. Here h is dimensionless Hubble constant also called Newtonian gravitational constant. Cosmological density parameter also shows the existence of dark matter.

Cosmic microwave background (CMB)

The Universe contains radiation at various wavelengths. The radiation background at various levels could be measured only after the advent of space astronomy.¹⁸ The Table 1 reveals that most dominant form of radiation background is the microwave background. The spectrum was discovered by A Penzias and R Wilson in 1964 and was found to come uniformly from all the directions with an effective temperature of about 2.7K. After Big Bang the universe, before the formation of stars and planets, was smaller, much hotter, and filled with a uniform glow from its white-hot fog of hydrogen plasma. According to the model, the radiation from sky comes from a spherical surface called the surface of last scattering. As the universe expanded, both the plasma and the radiation filling it cooled. When the universe cooled enough, Table 2 stable atoms could be formed. These atoms could no longer absorb the thermal radiation, and the universe became transparent instead of being an opaque fog. The photons that were around at that time have been propagating ever since, though growing fainter and less energetic, since the same photons fill a larger space and form Universe. This is the source for the term relic radiation, another name for CMBR. The spectrum of the CBR can be described very well by a blackbody function with the temperature T.^15–19 The present value is Table 3:

$T_0=(2.275\pm 0.001)K$

Anisotropy of the CMB radiation

Microwave background radiation (MBR) has primordial origin and therefore can reveal present and past history of the universe. Transition from radiation dominated universe to a matter dominated one marks the epoch of decoupling which imprinted their signature on the radiation background which are expected to survive even at present. However anisotropies in CMB have been observed over past few decades. The anisotropy of the CBR offers the best means for determining the curvature of the Universe, R_curv, and thereby the “total matter/energy density” of the Universe, Ω₀, according to the Friedmann equation:

${\Omega }_0-1=\frac{k}{R_{curv}^2{H}_0^2},$                                                 (9)

Where k is a curvature constant which can be chosen to take only three discrete values: ±1 and 0. According to the Friedmann equation, when the total matter/energy density of our Universe is equal to 1, the Universe is “spatially flat” (R_curv = ∞, or, equivalently, k = 0). While, for Ω₀ > 1 (Ω₀ < 1), the constant k should be +1 (−1) and we call the Universe “closed” (“open”).²⁰ W.Hue in his thesis work propose that free photons have information of early universe in the form of sound waves. The dark matter pressurize the photons wherever it is dominating this is indicated by anisotropy and oscillations observed in the data.²¹ See the Figure 3.

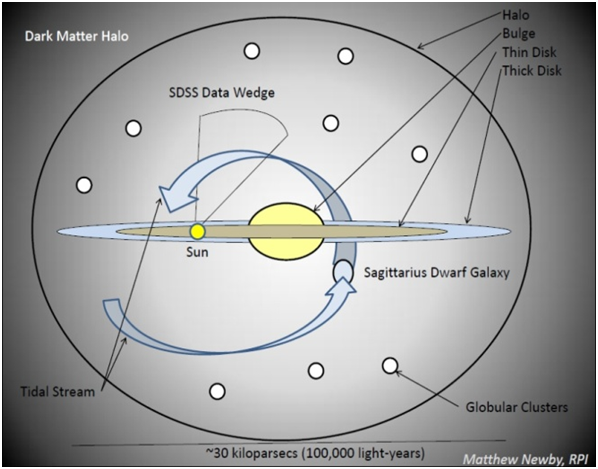
Figure 2 The modern view of the Milky Way galaxy contains four major components: The disk, bulge, stellar halo, and dark matter halo.

Figure 3 The angular power spectrum of the CMB temperature from three-year data of the WMAP satellite.

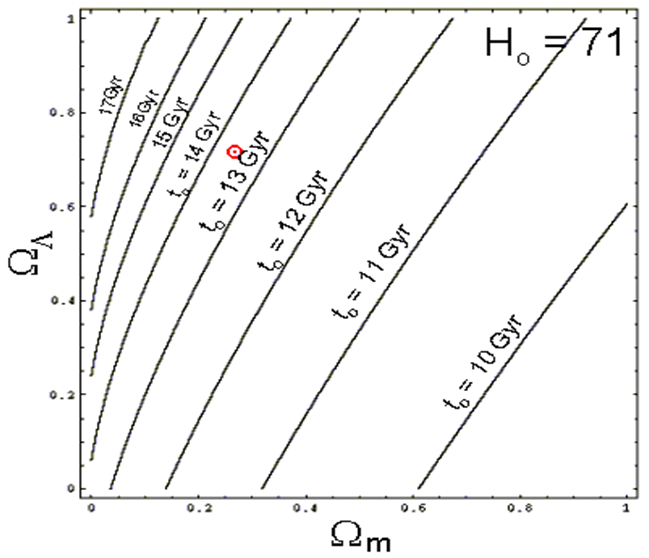
Figure 4 According to recent measurements, the universe contains a mysterious 'dark energy' in addition to normal matter, which causes the expansion speed to accelerate.

Figure 5 Plot of recession velocity and distance in Mpc. Courtesy: official web page of University of Massachusetts Boston.

Figure 6 Bending of light by gravitational field of a massive object.

In Fig.3 one can find that the anisotropy power, sometimes shown as ℓ(ℓ+1)C _ℓ/2π, oscillates (the so-called “gravity-driven acoustic oscillations”) with some “acoustic peaks”. Roughly speaking, the angular position of these peaks is a sensitive probe of the spatial curvature of the Universe: if our Universe is open (close), these peaks should lie at higher (lower) ℓ. Moreover, according to standard Big-Bang Cosmology, the higher the primordial matter density, the shorter the duration of the epoch of structure formation and thereby the larger fluctuations in the CBR , or, equivalently, the stronger these acoustic oscillations . Hence, the relative height of the first acoustic peak can be used to determine the “primordial matter density”. More details about the physics and the analyses of anisotropy of CBR can be found in Ref.²² As MBR is a relic of the early universe it’s spectrum and it’s anisotropies should reveal information about the past development of the universe.

Age of the universe

The age of the universe is the time elapsed between the Big Bang and the present time. Theories and observations suggest that the age of universe is between 13.5 and 14 billion years. The estimate of the age of the universe is obtained by measurement of background radiation and expansion of the universe. The ΛCDM/Concordance model describes the evolution of the universe from a very uniform, hot dense primordial state to its present state over a span of about 15 billion years of cosmological time. This model when extrapolated backward from the earlier well understood state, it quickly points to a singularity called the “Big Bang Singularity”. Friedmann equation relates the rate of change in the scale factor a(t) to the matter content of the universe. From this equation, we can calculate the total age of the universe by integrating this formula. The uncertainty range has been obtained by the agreement of a number of scientific research projects. Scientific instruments and methods have improved the ability to measure the age of the universe with a great accuracy. These projects included background radiation measurements and more ways to measure the expansion of the universe. Background radiation measurements give the cooling time of the universe since the big bang. Expansion of the universe measurements give accurate data to calculate the age of the universe. The age t0 is then given by an expression of the form

$t_0=\frac{1}{H_0}F\left({\Omega }_r,{\Omega }_m,{\Omega }_{\Lambda },\mathrm{.......}\right)$                             (10)

where the function F depends only on the fractional contribution to the universe's energy content that comes from various components. From this relation, it can be observed that the Hubble parameter H₀ controls the age of the universe, with a correction arising from the matter and energy content. A rough estimate of the age of the universe may be obtained from the inverse of the Hubble parameter,

$\frac{1}{H_0}={\left(\frac{H_0}{72km/(s.Mpc)}\right)}^{-1}\times 13.6Gyr$

The factor F depends on dark matter and dark energy contents in the universe. Therefore estimate of the age of the universe depends on the content of the dark matter in universe. According to refWilkinson Microwave Anisotropy Probe (WMAP) results the age of the universe has been estimated as.^16,18

$T_U={13.7}_{-0.2}^{+0.1}Gyr$ (11)

The age of the universe depends on the amount matter and the amount of dark energy. This contour plot shows the age derived from different possible values of the current matter density (x-axis) and dark energy density (y-axis); the actual values are thought to be 0.3 (matter) and 0.7 (dark energy), corresponding to the red dot.²³

Present expansion rate of the universe

According to the Hubble law

$H_0=\frac{v}{d}.=\frac{cz}{d}$                         (12)

where z is the redshift of the galaxy which is at distant d from earth. Here the velocity v can be determined by the redshift²⁵ The most accurate direct methods for measuring distances to distant objects d can be used to estimate the Hubble parameter H₀.²⁶ Currently, there are two methods for measuring extra galactic distances²⁶ (i) time delays between luminosity variations in different gravitationally lensed images of distant quasars and (ii) the Sunyaev-Zel’dovich effect which is The Sunyaev-Zel'dovich effect (often abbreviated as the SZ effect) is the result of high energy electrons distorting the cosmic microwave background radiation (CMB) through inverse Compton scattering, in which some of the energy of the electrons is transferred to the low energy CMB photons. Observed distortions of the cosmic microwave background spectrum are used to detect the density perturbations of the universe. Using the Sunyaev-Zel'dovich effect, dense clusters of galaxies have been observed.The present expansion rate of the Universe can then be given as

$H_0={73}_4^{+3}km/s/Mpc$

On very large scales Einstein's theory predicts departures from a strictly linear Hubble law. The amount of exit, and the type, depends on the amount and types of mass and energy of the universe. In this way a plot of recession velocity (or red shift) vs. distance (a Hubble plot), which is a straight line at small distances, can tell us about the amount of matter in the universe and make available vital information about dark matter.

Mass to light ratio

 In astrophysics and physical cosmology the mass to light ratio, normally designated with the symbol η which is the quotient between the total mass of a spatial volume (typically on the scales of a galaxy or a cluster) and its luminosity.²⁷

$\langle \frac{M}{L}\rangle =\eta \left(\frac{M_{\Theta }}{L_{\Theta }}\right)$

These ratios are often reported using the value calculated for the sun as a baseline ratio which is a constant η = 5133 kg/W equal to a solar mass divided by a solar luminosity. The mass to light ratios of galaxies and clusters are all much greater than η due in part to the fact that most of the matter in these objects does not reside within stars and observations suggest that a large fraction is present in the form of dark matter. Luminosities are obtained from photometric observations, correcting the observed brightness of the object for the distance dimming and extinction effects. The luminosity thus obtained is known as the bolometric luminosity. Masses are often calculated from the dynamics of the virialized system or from gravitational lensing. Typical mass to light ratios for galaxies range from 2 to 10 η  while on the largest scales, the mass to light ratio of the observable universe is approximately 100 η , in concordance with the current best fit cosmological model.

Gravitational lensing

 A gravitational lens is formed when the light from a very distant, bright source (such as a quasar) is "bent" around a massive object (such as a cluster of galaxies) between the source object and the observer. The process is known as gravitational lensing. Although Orest Chwolson is the first to discuss the effect,²⁸ the effect is usually associated with Einstein’s article on the subject in 1936.²⁹ Fritz Zwicky proposed in 1937 that the effect could allow galaxy clusters to act as gravitational lenses.³⁰ It was not until 1979 that this effect was confirmed by observation of the so-called "Twin QSO" SBS 0957+561.³¹

Strong lensing: Where there are easily visible distortions such as the formation of Einstein rings, arcs, and multiple images.

Weak lensing: Where the distortions of background sources are much smaller and can only be detected by analyzing a large number of sources to find coherent distortions of only a few percent.

 The lensing shows up statistically as a preferred stretching of the background objects perpendicular to the direction to the center of the lens.
Since galaxies are intrinsically elliptical and the weak gravitational lensing signal is small, a very large number of galaxies must be used in these surveys. The results of these surveys help in cosmological parameters estimation, and in the improvement of ΛCDM model. These studies can be used also in providing consistency check on other cosmological observations.

Microlensing: Where no distortion in shape can be seen but the amount of light received from a background object changes in time. The background source and the lens may be stars in the Milky Way in one typical case, and stars in a remote galaxy and an even more distant quasar in another case. 

Lensing as a tool to understand distribution of dark matter:

Keeton³² indicated that gravitational lensing is the best tool to understand the distribution of dark matter in the galaxy. Using the number and sizes of observed gravitational lenses, he derives upper limits on the dark matter content of elliptical galaxies. On the average, dark matter can account for not more than 33% of the total mass within one effective radius (R_e) of elliptical galaxies, or 40% of the mass within 2Re (95%confidence upper limits). he shows that galaxies built from Cold Dark Matter (CDM) mass distributions are too concentrated to comfortably satisfy these limits; a high-density (Ω_M = 1) CDM cosmology is ruled out at better than 95% confidence, while a low-density, flat cosmology is only marginally consistent with the lens data. Thus, lensing adds to the evidence from spiral galaxy dynamics that CDM mass distributions are too concentrated on kiloparsec scales to agree with real galaxies, and extends the argument to elliptical galaxies.³³