The article provides the results of the calculations of the mathematical model (theoretical) and experimental studies of the volt-ampere and watt ampere characteristics of the regimes of the solar mobile photoelectric station, depending on internal and external factors, the degree of orientation and angle of the azimuth and zenith in the sun in the aris environment of Turkmenistan.

Keywords: solar mobile station, photoelectric converter, mathematical model, solar tracking systems, volt and watt ampere characteristics, Turkmenistan.

In the context of a change in the climate of the use of renewable energy sources (renewable) for reducing anthropogenic loads on the environment, it is an urgent problem.¹ The introduction of renewable energy plants in a particular region is necessary for a technical and economic justification (feasibility study) to assess energy efficiency.

Methods of mathematical modeling make it possible to systematize, classify the results of research based on their design and estimate documentation for the creation and implementation of solar and energy technologies, and methods of analysis statistics allows you to predict the effect of atmospheric phenomena on the energy production of the solar photoelectric installation. To ensure the maximum arrival of solar radiation to the working surface of the photoelectric module (FEM) and increase the energy production of solar plants (SP), it is possible by tracking the sun depending on the latitude of the terrain and season. The use of Sun tracking systems can increase the output power of FEM in the daily interval of electric energy generation. There are various systems for tracking the sun with partial (azimutal) or complete (azimutal and anti-aircraft) orientation.^1,10-12

The purpose and objectives of research work is to compile a mathematical model, scientifically justify, systematize, create a mobile solar station and calculate the solar and energy indicators of the solar station, depending on the angle of inclination of tracking systems and without tracking and the methods of mathematical statistics, predict energy resource potentials.

Research methods are based on a systematic approach to a compiled mathematical model for a solar mobile photoelectric station.

The methodological base is theoretical calculations by the methods of the mathematical model, experimental studies of the energy parameters of the solar station under various conditions of tracking the sun.

Calculation methodology: The most effective method of studying the solar station is to simulate the method of mathematical modeling, which allows you to compare full -scale experimental research the effect of illumination on the energy characteristics of the solar installation. This allows you to consider a large number of parameters, reduce the costs of time and means to conduct the necessary calculations and research.

The scientific novelty of the study is systematized, scientifically substantiated by the energy parameters of the solar station based on the mathematical model and the methods of statistical analysis compiled regression equations for predicting the energy parameters of the mobile station for the compilation of the feasibility study for the natural and climatic conditions of Turkmenistan.

The mathematical modeling was based on the classical model of a photoconverter with a pn junction:¹¹

$U=\frac{\text{A K T}}{q} In \left[\frac{J_{ф}-J}{J_o}+1\right]-JR$   (1)

where U is voltage, V ; k is Boltzmann's constant; T - operating temperature of the solar cell, K ; q - electron charge; Jf - photocurrent, proportional to the intensity of solar radiation _I incident on the surface of the solar cell, ( _Jf / I = const ) A /cm² ; J - current, A/cm² ; J _o – reverse saturation current, determined by the properties of the original semiconductor, was determined from expression (1) under the condition J = 0 and U = U _xx , A/cm² ; R - internal electrical resistance, Ohm/cm² ; A is the dimensionless curvature parameter of the current-voltage characteristic (volt-ampere characteristic), A = 1….2.

To study the operating modes of control systems with solar cells, a mathematical model was developed, implemented in a software environment. In order to test it, a current-voltage characteristic and a volt-watt characteristic (VVC) were constructed for a PV module consisting of parallel-connected blocks under standard lighting conditions AM1 I _o =1000 W/m2 ^and operating temperature. Photocells made of monocrystalline silicon have the following characteristics: J _{o kz} =2.74 A/m² ; U _xx =22 V ; R= 1Ohm cm² ; area S=0.3792 m² . The photovoltaic module, according to the passport data, produces maximum power P _max = 49.4 W , U _xx = 20.6 V , I _short = 2.4 A , optimal operating voltage U _opt = 16.3 V and current J _opt =2.75 A power P _opt = 44.8 W.

As can be seen from Figure 1a, the obtained theoretical calculations of the current-voltage characteristics (volt-ampere characteristics) of the mathematical model coincide with the passport data, which confirms the adequacy of the developed model.

However, the actual characteristics of solar cells differ significantly from the standard ones due to changes in environmental parameters (solar radiation intensity and air temperature), which depend on the geographic location of the intended operation of the installation, time of year, day and degree of orientation of the solar control system to the Sun.

The influence of changes in the intensity of solar radiation and operating temperature on the current-voltage characteristics of solar cells can be written in the form of expressions:^5-9,11

$J_{k.z.}=J_{oshortcircuit}+\Delta J_I+\Delta J_T$   (2)

Uxx _{. _} = U _{o xx .} + Δ U _{I 1} + Δ U _{I 2} + Δ U _T  (3)

where Jo _kz And Uo _xx - initial short circuit current and open circuit voltage, measured under standard lighting conditions AM1( I _o = 1000 W/m ² ) and operating temperature ( T =  25 ° C 0 ); D J _I , D U _{I 1} , D U _{I 2} - corrections taking into account changes in solar radiation flux density; D JT , D UT - corrections taking into account changes in operating temperature:

$\Delta J_I=\frac{I- I_o}{I_o} J_{o к.з.}$   (4);

$\Delta U_I{}_2=-\text{Δ} J_{I }{R}_p$   (5);

$\Delta U_I{}_2=\text{к}\lg \left(\frac{I}{I_o}\right)$   (6);

$\Delta J_T={\beta }_I J_{o к.з.} \left(T-T_o\right))$   (7);

$\Delta U_T{=}_{ }{\beta }_U U_{\text{xx}} \left(T-T_o\right))$   (8);

where R _{I 1} is the series resistance of the element; k - coefficient depending on the type of solar cell, 0.5≤ k ≥1.5;² , β _I , β _u - temperature coefficients of current and voltage, 1/°С.

When determining the intensity of solar radiation (direct, diffuse and total) on a horizontal surface during mathematical modeling, long-term observational data were used.¹³ To exclude intervals whose intensities are unknown, the polynomial approximation method was used.^2-7,11,12

The total intensity of solar radiation on a stationary inclined surface oriented to the south was calculated by the expression:^10-12

$I_H=I_{п}\frac{cos\epsilon }{\cos \theta }+I_{Д}\frac{\left(1+\cos \beta \right)}{2}+ \rho \left(I_{П}+I_{Д}\right)\frac{1-cos\beta }{2},$   (9)

where I _P , I _D , - intensity of direct and scattered (diffuse) solar radiation on a horizontal surface, W/m²; q  - the angle between the directions to the Sun and zenith in degrees, determined by formula (10); x  - the angle between the direction to the Sun and the normal to the inclined surface oriented south in degrees determined by formula (11); b  - the angle of inclination of the surface under consideration to the horizon in degrees; r  is the reflection coefficient (albedo) of the Earth’s surface and surrounding bodies.¹¹

cos q =  sin d  sin j +  cos d  cos j  cos w,    (10)

cos x =  sin( j -b  ) sin d +  cos( j -b  ) cos d  cos w ,  (11)

where d  is the declination of the Sun, determined by Cooper’s formula in degrees,¹ j  is the latitude of the area, in degrees; w  - hourly angle of motion of the Sun, in degrees.

The hour angle was calculated using the formula:⁵

ω=(15 ^o hour ^-1 )( t solar-12),  (12)

where t solar is local solar time in hours.

Calculation of the total intensity of solar radiation at the receiver, located at an angle b  and oriented towards the Sun in only one direction coordinate (azimuthal tracking) was carried out according to formula (9), with the difference in finding the angle between the direction to the Sun and the normal ( i is used instead of x  ). This angle was determined by the formula:^8-11

cos i = sinβ [ cos d ( sin j cos a _П cos w+  s in a _П   sin w )- s in d cos j cos a _П ]+

cos β[cos d cos j cos w  +  s in d sin j ] ,  (13)

where a _P - azimuth of the receiver.

When tracking the Sun in azimuth, the azimuth of the receiver is equal to the azimuth of the Sun ( a _p =a   ) and was determined by the formula:6-11

$a=\left(\frac{\cos \beta \sin \phi }{\cos \alpha }\right)$   (14)

where a  is the altitude angle of the Sun, determined by the formula:  

Jf / I = const $W/m{2}^{and }a= arcsin(sin\delta sin\phi + cos\delta cos\phi cos\omega )\Rightarrow \alpha = arcsin(cos\theta ).$   (15)

  W/m²; I _KZ - a short -circuit current force, a; U_hh

The total intensity of solar radiation at full surface orientation was calculated using the expression:¹

$I_{\text{op}}=\frac{Iп}{\cos \theta }+I_{д }\frac{(1+\cos \theta )}{2}+ \rho \left(I_{п}+I_{д}\right)\frac{1-\cos \theta }{2}$   (16)

To calculate the ambient air temperature, we used hourly data on ambient air temperature given in the reference book¹³⁰ and used the analytical dependence of the change in air temperature over time, taking into account the average daily amplitude, the period of change in air temperature.^7-12

All the above expressions were taken into account in the developed mathematical model. Figure 1 shows the results of theoretical calculations based on a mathematical model of the current-voltage characteristic (VAH) and watt-ampere characteristic (GVC) of a solar cell:

Figure 1 Characteristics of the PV module for theoretical calculations, standard without tracking and oriented to the South: a – VAH on May 21 at 10 o’clock; b – GVC.

A mobile solar photoelectric station was developed, representing a photoelectric module representing on the one hand in the form of a suitcase (diplomat), on the other hand, equipment belonging to the station (inventory, battery, angular and legs for fastening the station) are built -in. Studies of the mobile station were conducted in the Daikhansky associations of the Hatab of the Atamyrat Etrap (district) of the Lebap Velayat (region) of the Southeast Turkmenistan: 38° northern latitude; 53° east longitude. Experimental studies were carried out in two modes: the solar installation is oriented to the south with an angle of inclination of 60°; the station is oriented to the south with a change in the angle of inclination from 0° to 60° and tracking the solar clock orientation. The following energy parameters are calculated on the basis of the compiled mathematical model: R - solar radiation, W/M2; I KZ - a short -circuit current force, a; Uhh - idle voltage, in; I wholesale - optimal current strength, a; U wholesale - optimal voltage, c; R Optimal power, W; η- efficiency, %. The results of experimental studies are given in Table 1 and in Figure 2.

Mathematical methods of statistical analysis allow you to systematize and classify the results of studies and on their basis carry out zoning, determine the similarity and difference between the processes of interaction in various natural conditions, a likely dependence between the phenomena, to highlight the leading factors acting on the development of the process of forecasting energy transformation from the angles of tracking.

When studying the relationship between two random values, correlation analysis is used. As a tightness of this connection, the correlation coefficient of Pieron, R² is used. As a correlation analysis, we consider the influence of the angle of solar radiation on the volt-ampere (VAH), watt ampere (GVC) energy characteristics.

Below are the found values of R², which indicate the accuracy of the calculations of two functional values of solar radiation on VAH and GVC energy characteristics. The mathematical interconnection is expressed by regression coefficients, we divert the regression equation in the form of y = a+bx, where A is the initial orderly and gives the value of at x = 0, b is the regression coefficient showing how much the amount of coal is changed if the x changes to unit. In our calculations, the potentials of solar radiation depending on the influence of the angle on energy production. The obtained regression of the equations look like. Regression dependence and correlation coefficient in theoretical calculations based on a mathematical model of a mobile station of a photovoltaic station:

current-voltage characteristics is equal to:

y = -0.1127x + 3.7694; R² = 0.4961;    (17)

volt-watt characteristic:

y = 10.022 x + 8.551; R² = 0.3486.   (18)

Regression dependence and correlation coefficient in experimental studies of a mobile station of a photovoltaic station:

CVC y = -0.104x + 3.0434; R² = 0.6203;   (19)

I-V characteristic with sun tracking: y = 0.0818x + 2.4356; R² = 0.5804;    (20)

VVH without sun tracking oriented south:

y = 7.1586x + 5.8938; R² = 0.2361;    (21)

VVH with sun tracking with 60 degree rotation:

y = 7.9471x + 8.2286; R² = 0.2599;   (22)

Thus, the obtained regression equations (17-22) of the technical energy potentials of the VAH and the GDC of the Solar Station, depending on and without monitoring. The results will contribute to the forecasting of various sunny and energy technological installations, as well as in the preparation of design estimates and technical and economic justification.

The results of modeling the operation of the PV module, the characteristics of which are given above, for the climatic conditions of the south-eastern regions of Turkmenistan ( j  = 38°), at 10 o'clock local solar time on May 18 are presented in Figure 2. The analysis shows that the output power of the solar cell module with a solar tracking system at the specified time is significantly greater than the power of the stationary one. Full orientation of the module to the Sun gives almost the same characteristics as with partial (azimuthal) orientation. Consequently, carrying out such comparative modeling for a year-round period will make it possible to assess the feasibility of using automated tracking systems in control systems with solar cells.

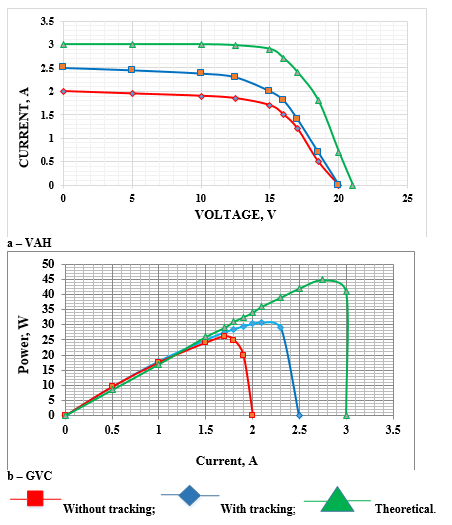
Figure 2 Energy characteristics of FEM in theoretical calculations, wagging and without monitoring the standard with azimutal orientation south at an angle to the horizon of 60 °, and - VAH on May 18 at 10 o’clock; B - GDC, where

The mathematical model allows us to evaluate the influence on the output characteristics of the PV module, both internal (number of series and parallel connected elements, internal resistance) and external factors (intensity of solar radiation, air temperature, degree of orientation of the PV module to the Sun depending on the time of year and day). A comparison of the solar radiation intensity values obtained during modeling with the data given in Table 1 and Figure 1 showed that the error does not exceed 12%, and the ambient temperature with the data given in the climate reference book - 5%. Comparison of Jo _{K values . Z. _} , Uo _ХХ , Pmax obtained during modeling with the values given in the passport data of the PV module confirms the adequacy of the developed model. With tracking, power and current increases by 15%, and, naturally, efficiency increases by 1%. at 10 am. The mathematical model can be used to assess the feasibility of using automatic tracking systems in control systems with solar cells.

None.

None.

1. Penjiyev AM. Eco–energy resources of renewable energy sources: Monograph/ –M.: RUSAINS, 2023, 400 p.
2. Penjiyev AM. Climate change and possibilities for reducing anthropogenic loads. Monograph. LAMBERT Academic Publishing, 2012.
3. Penjiyev AM. Ecological problems of desert development. Monograph, Publisher: LAP LAMBERT Academic Publishing. 2014, 226 p.
4. Penjiyev AM. Planning for the development of photoenergy in Turkmenistan. Environmental planning and management. 2007.
5. Penjiyev AM. Expected environmental and economic efficiency of using a photovoltaic station in the desert zone of Turkmenistan. Alternative energy and ecology – ISJAEE. 2007, pp. 135–137.
6. Penjiyev AM, Astanov NG. And the use of solar energy installations in protected areas of Turkmenistan to improve the arid ecosystem. International scientific journal Alternative Energy and Ecology. 2011;12(104):26–32.
7. Penjiyev AM. Renewable energy and ecology (summarization of articles). International scientific journal “Alternative energy and ecology. 2014;8(148):45–78.
8. Penjiyev AM. Clean Development Mechanism: energy efficiency priorities in Turkmenistan. International scientific journal Alternative Energy and Ecology. 2009;10(78):142–148.
9. Penjiyev AM. Prospects for alternative energy and its environmental potential in Turkmenistan. International scientific journal “Alternative energy and ecology. 2009;9(77):131–139.
10.  Rauschenbach G. Handbook on the design of solar panels: Transl. from English – M.: Energoatomizdat, 1983;360.
11. Strebkov DS, Penjiyev AM, Mamedsakhatov BD. Development of solar energy in Turkmenistan. Monograph. M.: GNU VIESKh, 2012.
12. Use of solar energy. Edited by Professor Rybakova L.E. Ashgabat: Ylym, 1985.
13. Scientific and applied reference book on the climate of the USSR. Series 3, parts 1–16, issue. 1– 30, Л.: 1989, 502 pp.