In order to improve the imaging quality of seismic profile, a new method based on difference is proposed to eliminate the azimuthal moveout. Test results shows that the resolution of the model and real data have been improved significantly in both the prestack gather and the stack profile. The new method proposed is valid and implemented simply.

Keywords: anisotropy, difference, azimuth, moveout correction

Due to the fast development of seismic exploration, azimuth anisotropy greatly attracts geophysicists’ attention; especially wide azimuth acquisition is extensively applied in recent years. It is well known that the traveling time variation with azimuth is main exhibition in seismic record due to the media anisotropy which enhances the difficulty of processing and influencing the identity of the small structure. In order to remove the effects of the azimuth anisotropy (traveling time), some geophysicists have carried out a great deal of research work and have already obtained obvious achievement, such as Lehmann et al.,¹ removed azimuth moveout by velocity analysis based on azimuth gather. Tsvankin et al.,² introduced coefficient of anisotropy in conventional velocity analysis. Alkhalifah et al (1998) introduced azimuth moveout (AMO) correction as a single operator to correct for azimuth variations (and dip) in homogeneous isotropic media. Rosales et al.,³ extended AMO operator to converted wave field. James⁴ removed the azimuth moveout by converted wave splitting estimation. In this paper, we introduce a new method-difference to eliminate the azimuth moveout, this method is effective to improve the effect of azimuth anisotropy, more important it is easy to implement.

In ACCP((Asymptotic common conversion point)）gather, if azimuth anisotropy induced by media anisotropy doesn’t exist, the object layer’s traveling time would be fit for hyperbola well, similarity, the object layer wouldn’t fit for hyperbola, if media anisotropy exists. But the media is anisotropy in reality, so the azimuth anisotropy must be taken in consideration, especially in strong anisotropy area in actual processing, such as velocity analysis, normal moveout correction, dip moveout correction and so on. Difference is a simple method to eliminate azimuth anisotropy, we assume there are N azimuths existed applied NMO in ACCP gather, N is odd, and also assume the sum of all azimuth moveout is zero or close to zero, this hypothesis is very suitable for azimuth moveout correction and easy to come true, so the $i^{th}\left(i=\left(N-1\right)/2+1\right)$ azimuth moveout can be expressed:

$T_i=T_i-\frac{{\displaystyle \sum _{j=1}^N{T}_j}}{N}$  (1)

Where $T_i$  is the i^th azimuth moveout, $T_j$ is one of the azimuths in N azimuths. The two adjacent azimuth moveout $\left({\Delta }_{\text{i}}\right)$ can be described as:

${\Delta }_{\text{i}}=T_i-T_{i-1}$  (2)

N-1 equation can be acquired according to the formula (2) in N azimuths as follows:

${\Delta }_{i-\frac{N-1}{2}+1}$

$\begin{array}{l}{\Delta }_{i-\frac{N-1}{2}+2}=T_{i-\frac{N-1}{2}+2}-T_{i-\frac{N-1}{2}+1}\\ \cdots \cdots \cdots \cdots \end{array}$

${\Delta }_{i-1}$

$\begin{array}{l}{\Delta }_i=T_i-T_{i-1}\\ \cdots \cdots \cdots \cdots \end{array}$

${\Delta }_{i+\frac{N-1}{2}-1}$

${\Delta }_{i+\frac{N-1}{2}}$  (3)

According to the formula (3) and formula (1), we can compute the ith azimuth moveout by the residual azimuth moveout, it can be expressed as follows:

$T_i=\frac{-1}{N}{\displaystyle \sum _{j=1}^{(N-1)/2}\left[(\frac{N-1}{2}-j-1)({\Delta }_{i+j}-{\Delta }_{i-j-1})\right]}$  (4)

From this formula (4), we can conclude azimuth moveout can obtain azimuth by difference of adjacent azimuth residual moveout, while azimuth residual moveout can be got by correlation of adjacent record. We illustration an example: N=9, i=5, The fifth azimuth moveout can expressed as follows:

$T_5=-\frac{1}{9}{\displaystyle \sum _{j=1}^{j=4}(5-j)({\Delta }_{5+j}-{\Delta }_{6-j})}$  (5)

In actual data process, the process can be decomposed as follows:

1. Make sure the object layer in stack section and reverse NMO
2. Check the number of azimuth and the distribution of azimuth in ACCP gather, if the number is few and the distribution is not even, we can format super-gather by adjacent ACCP to guarantee enough amount and even distribution of azimuth
3. ISort trace by azimuth in ACCP and make a circle correlation between adjacent azimuth trace in ACCP, the azimuth residual moveout can be acquired
4. Computing every azimuth moveout by the formula (4). Apply azimuth moveout to trace.

To show the validity of the method, we design a three-dimensional model by anisotropic elastic wave equation based on grid finite difference to obtain model record. The parameters are as follows: the thickness of coal bed is 50 meters, the density of fracture is 0.3 and the fracture is parallel to the Y axis, the detailed parameters are exhibited in the left of the Figure 1. The geometry is radial (seeing in the right of the Figure 1): The source is located in the centre of model, 24 receiver lines radiate from the centre and the included angle between two adjacent lines is 15°, each line consists of 600 receivers separated by 1meter. The X component, namely the radial component, and the Z component are like the azimuth gathers showing in the left and the right of the Figure 2, respectively.^5,6 We will discuss how to remove the anisotropic influence of velocity based on the common offset gathers. An example common offset gather with 300meter displayed in the up of the Figure 3. The azimuth values range from 0°to 345°and the interval is 15 degree. Seeing from the up of the Figure 3, the object event, represented by blue, fluctuates from 0 to 345 degree, like a sinusoid to a large extent, which is accounted for and produced by the anisotropic effect.^7,8 The azimuth moveout distribution looks like a sin curve, it meet the hypothesis that the sum of azimuth is zero or close to zero. The biggest moveout is more than 2 milliseconds, it must be degraded the resolution of seismic without azimuth moveout correction. Seeing from the result gather, showed in the bottom of the Figure 3,⁹ which is applied azimuth moveout correction by difference, the fluctuation of the object event drawn by blue is disappear and the phases are coherence. An actual P-SV data is tested by this method, Figure 4 is a stacked section and the objected layer lies between 1000ms and 1200ms, which process the flow of NMOby ACCP and stack, Figure 5 is also stacked section which pass azimuth moveout correction based on difference between nmo by ACCP and stack. To stack traces after azimuth moveout correction by the proposed method can guarantee higher resolution and easier to identify the small structure than conventional process without azimuth correction.^10–12

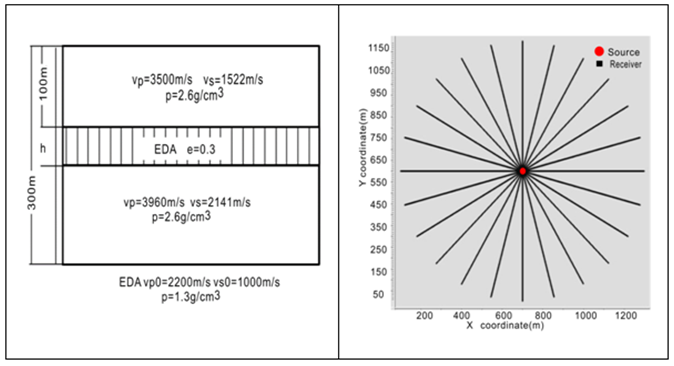
Figure 1 The geological model (Left) and the radial geometry (Right).

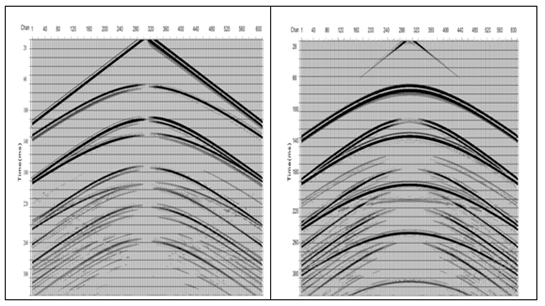
Figure 2 X component (Left) and Z component (Right) of the 45° azimuth gathers.

Figure 3 The common offset gathers before (up) and after (bottom) azimuth move out correction by difference method (offset is 350 meter).

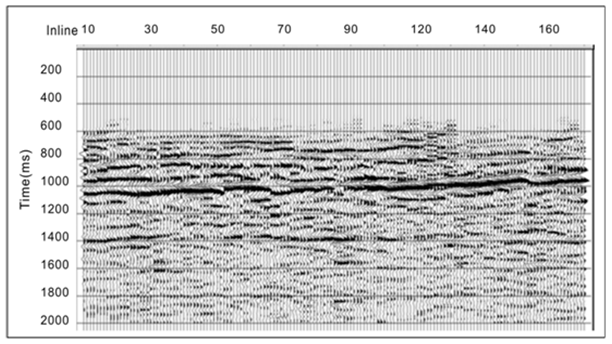
Figure 4 The stacked section (ACCP) (before azimuth correction, Inline 31，Xline 10-160).

Figure 5 The stacked section (ACCP) (after azimuth correction, Inline 31, Xline 10-160).

The moveout which causes by azimuth anisotropic degrades the precision of seismic processing, such as velocity analysis, NMO, stack, DMO and so on. Difference is a effective way to eliminate azimuth anisotropy moveout. In this method, we assume N azimuth moveout is zero or close to zero in ACCP. The hypothesis is better which the distribution of azimuth is more even, the time difference is stable and easy to achieve. This method is especially useful in wide azimuth acquisition. This method narrated in the paper aims to the object layer and the dependence of velocity. If there are many layers, layer stripping should be taken into account.

This study was  financially supported by China Geological Survey projects No. DD20189132.

1. Lehmann H J, Houba W. Practical aspects in the determination of 3-D stacking velocities. Geophysical Prospecting. 1985;33(1): 34–51.
2. Tsvankini I, Thomsen L. Nonhyperbolic reflection moveout in anisotropic media. Geophysics. 1994;59(12):45–55.
3. Rosales DA, Biondi B. Converted-wave azimuth moveout. Geophysics. 2006;71(99):55–66.
4. James L, Simmons J. Converted-wave splitting estimation and compensation. Geophysics. 2009;74(37):12–21.
5. Lin Yun. Application of wide-azimuth seismic exploration. OGP. 200;38(4):350–357.
6. Lin Yun, Gao Jun, Sun Desheng. Analysis and appreciation of wide/narrow azimuth exploration cases (I). OGP. 2005;40(3):305–308.
7. Gou Jinwei, Yao Chen, Yu Guangming. Probe into method on exam of coal-bed fractures with transformed wave. Coal Geology of China. 2001;13(3):5256–5261.
8. Mark Paul Harrison. Processsing of P-SV Surface-Seismic Data: Anisotropy Analysis. Dip Moveout and Migration. PHD thesis. University of Calgary. Canada. 1992.
9. Tessmer G, Behle A. Common reflection point data stacking technique for converted waves. Geophysical Prospecting. 1988;36(7):671–688.
10. Tariq A, Biondo B. The azimuth moveout operator for vertically inhomogeneous media. Stanford Exploration Project Report. 1998;97:95–116.
11. Pei Zhenglin, Dong Yu Shan, Peng Suping. Numeric simulation of azimuth anisotropic characters of elastic wave field in fractural coal seams. OGP. 2007;2(6):665–672.
12. Pei Zhenglin. Numeric simulation of 3-wave splitting and splitting in layered anisotropic media. OGP. 2006;41(1):17–25.