The propagation of the ion-acoustic shock waves (dissipative waves) are presented in a plasma consisting of fluid ions and cold and hot electrons. Cold and hot electrons are considered as Maxwellian and kappa distribution functions, respectively. Using reductive perturbation technique, Korteweg-de-Vries-Burger (KdVB) and Burgers equations are derived for shock waves in the present plasma model. It is found that both positive (compressive) and negative (rarefactive) ion-acoustic shock waves can be propagating in present medium. Finally, the influence of different parameters on both these shock waves are studied numerically. Our results are important for the electrostatic shock wave structures in space plasmas.

Keywords: two-temperature plasmas, K-dVB equation, burgers equation, ion-acoustic shock waves, superthermal electrons

One the most important subjects in the plasma physics is the propagation of nonlinear waves that can be described by different partial differential equations as Korteweg-de Vries (K-dV) equation,¹ Korteweg-de-Vries Burger (K-dVB) equation² and the nonlinear Schrödinger equation (NLSE).³ Electrostatic solitary waves (solitons) that described usually by K-dV equation derived by balancing the nonlinearity of the medium with the wave dispersion. On the other hand, for a dissipative media, the balance between nonlinearity and dissipation may lead to formation of the shock structure. Shock waves in plasmas are different from these in normal gases. Because of presence of charge particles, certain types of shock waves can exist in a plasma. Shock waves can also be observed in space^4–6 and experimental^7–9 plasmas. Plasma with two-distinct group of electrons (cold and hot) can also be seen in space plasmas.^10,11 Many papers have investigated the propagation of ion-acoustic solitons in a plasma with two types electrons.^12–14 In such as media the theoretical and experimental results have been shown that the characteristics of solitary waves strongly modified by the presence of  minority population of cold electrons.^15–17

However, in the space and astrophysical plasma environments such as solar wind, magnetosphere and auroral zone plasmas, particles are often characterized by velocity distributions that are not Maxwellian and modeled by a kappa (or generalized Lorentzian) distribution function.^18–20 Recently, the propagation of ion acoustic solitons in collisionless plasmas with high-energy particles (represented by kappa distribution) is investigated in many papers.^21–27 In addition, the existence and propagation of ion acoustic solitons in a plasma with two-temperature kappa distributed electrons have been investigated in.^28–30 They have been studied treatment of small and arbitrary solitary waves by deriving an energy integral equation. On the other hand, it should be remarked that a medium with dispersive and significant dissipative properties supports another solitary wave such as shock waves instead of solitons. Many researchers have studied shock wave structures in superthermal plasmas. For example, Sultana et al.³¹ have studied dynamic of shock waves in a collisionless electron-ion plasma with superthermal electrons which is modeled by kappa distribution function. They obtained that higher deviations from a pure Maxwellian behavior induced shocks which were larger, narrower and faster.³¹ Ion-acoustic shock waves in a plasma consisting of electrons, positrons and ions with Boltzmann distributed positrons and superthermal electrons were also studied by Pakzad.³²

It is observed that an increasing positron concentration decreases the amplitude of the waves. The characteristics of ion-acoustic shock waves in electron-positron-ion plasma were investigated in³³ where electrons and positrons were modeled by kappa distribution function. It is seen that the amplitude of ion-acoustic shock waves decreases as the positron density and electron temperature increases.³³ In addition, Shah et al.³⁴ have investigated the effect of  positron beam on the ion-acoustic shock wave in a plasma consisting of inertial ions and superthermal electrons and the positron beam. They have derived the spectral index of the superthermal electrons, and concentration of impinging positron beam have significant effects on both the amplitude and steepness of the ion-acoustic shock wave. The oblique propagation of ion-acoustic solitons in magnetized plasmas containing kappa distributed hot and cold electrons have examined by several authors.^35,36 In addition, Bains et al.³⁷ studied the propagation of ion-acoustic shock waves in a magnetized plasma consisting of cold ions and two different temperature kappa distributed electrons. It is seen that all plasma parameters such as the density of hot electrons, the superthermality of electrons, the obliqueness, the strength of external magnetic field and the ion kinematic viscosity increase the shock height. The investigation of dust ion acoustic shock waves in two temperature plasmas has attracted significant attention among researchers.^38–40 However, the properties of shock waves in a plasma containing cold ions, cold (Maxwellian) and hot (superthermal) electrons has not been reported so far in papers. Therefore, in this paper using reductive perturbation technique, we have investigated shock structures from the solutions of the K-dV Burgers equation. Both the cases with quasi-neutrality condition as well as Poisson’s equation have been considered to observe such type of structures. It has been noticed that with the presence of the dissipation terms, a significant variation of the structures is observed. The layout of this paper is as follows: in section 2, we present basic equations and obtain K-dVB and Burgers equations. Also, these equations are solved by tanh method. Numerical results are given in Sec. 3. Finally, in Sec. 4 the conclusions of the present work are discussed.

We consider one nonlinear three -component homogeneous plasma consisting of cold fluid ions, cold and hot (superthermal) electrons. Here, it is assumed that cold and hot electrons have Maxwellian and kappa distribution functions, respectively. In equilibrium, the quasi-neutrality condition is as $n_{c0}+n_{h0}=n_{i0},$   where $n_{c0}$ , $n_{h0}$ and $n_{i0}$  are theunperturbed number densities of the cold electrons, hot electrons and ions, respectively. It is assumed that the present medium has dissipative properties in addition to what mentioned earlier. The fluid model for the ions is described by the following continuity and momentum equations:

$\frac{{\partial }_{ni}}{\partial t}+\frac{\partial }{\partial x}\left(n_i{u}_i\right)=0,$     (1)

$m_i{n}_i\frac{\partial u_i}{\partial t}{m}_i{n}_i{u}_i\frac{\partial ui}{\partial x}+e{n}_i\frac{\partial \Phi }{\partial x}-m_i{n}_i{u}_i\frac{{\partial }^2{u}_i}{\partial x^2}=0.$     (2)

The system is closed by Poisson’s equation:

$\frac{{\partial }^2\Phi }{\partial x^2}=4\pi e\left(n_c+n_h-n_i\right).$     (3)

In the above equation n_c, n_h and n_i are the density of cold electrons, hot electrons and ions, respectively.  is the velocity of ions; and is the electrostatic potential. An ad hoc damping term is introduced in the momentum equation, involving the (ion) kinematic viscositye is the magnitude of the electron charge and is the ion mass. In our analysis, all parameters are normalized as follows, the ion and cold (hot) electron densities by the unperturbed ion density n_io the ion velocity by $c_s={\left(k_B{T}_e/m_i\right)}^{1/2},$  the electrostatic potential by ${\phi }_0=\left(k_B{T}_e/e\right),$ the space and time are normalized by Debye length ${\lambda }_D=C_s/{\omega }_{pi}$ and ion plasma frequency ${\omega }_{pi}={\left(e^2{n}_{i0}/{\epsilon }_0{m}_i\right)}^{1/2}$  respectively. Therefore, the basic normalized equations in this system can be written as:

$\frac{\partial n}{\partial t}+\frac{\partial }{\partial x}\left(nu\right)=0,$     (4)

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+\frac{\partial \phi }{\partial x}-\eta \frac{{\partial }^{2}u}{\partial x^2}0,$     (5)

$\frac{{\partial }^2\phi }{\partial x^2}-n_c+n_h-n$     (6)

Where the normalized (ion) kinematic viscosity variable is defined as $\eta ={\eta }_i/\left({\omega }_{pi}{\lambda }_D^2\right).$  The normalized number densities of electrons are given by

$nc=\alpha e^{\sigma \phi }$ $n_h=\beta {\left(1-\frac{S\phi }{k-3/2}\right)}^{-k+1/2},$     (7)

Where $\alpha =n_{c0}/n_{i0},$   $\beta =n_{c0}/n_{i0},$ $S=T_e/T_h={\left[\left(1-\beta \right)\tau +\beta \right]}^{-1}$ and $\sigma =T_e/T_c=\tau S,$  where T_c and T_h  are the temperature of cold and hot electrons, respectively and the variable $\tau$  is defined as hot to cold electron temperature ratio, namely $\tau =T_h/T_c.$  The effective temperature T_e given as

$T_e=T_c{T}_h{\left[\left(\frac{n_{c0}}{n_{i0}}\right)T_h+\left(\frac{n_{h0}}{n_{i0}}\right)T_c\right]}^{-1}.$     (8)

Here k is the spectral index that measuring deviation from Maxwellian equilibrium and valid for $k>3/2.$

Ion-Acoustic shock waves

We are now interested for investigation propagation of shock waves in present plasma model. Therefore, we shall employ reductive perturbation technique.⁴¹ The independent variables can be stretched as

$\xi ={\epsilon }^{1/2}\left(x-\lambda t\right)$  and $\tau ={\epsilon }^{3/2}t,$  (9)

Where $\epsilon <<1$ is a small parameter and $\lambda$  is the unknown linear phase velocity to be determined later. Also, the independent variables, and can expanded as follow

$\left(\begin{array}{l}n\\ u\\ \phi \end{array}\right)=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)+{\displaystyle {\sum }_{l=0}^{\infty }\left(\begin{array}{l}{\epsilon }^{l+1}{n}_{l+1}\\ {\epsilon }^{l+1}{u}_{l+1}\\ {\epsilon }^{l+1}{\phi }_{l+1}\end{array}\right)}.$     (10)

In continue, substituting equations (9) and (10) into equations (4)– (6), and isolating distinct orders in $\epsilon ,$  we obtain a Korteweg-de Vries Burgers (K-dVB) type equation in the form

$\frac{\partial }{\partial \tau }{\phi }_1+A{\phi }_1\frac{\partial }{\partial \xi }{\phi }_1+B\phi \frac{{\partial }^3{\phi }_1}{\partial {\xi }^3}-C\frac{{\partial }^3{\phi }_1}{\partial {\xi }^2}=0$     (11)

Where

$A=-\left[\beta C_2{S}^2+\frac{1}{2}\left(1-\beta \right){\sigma }^2\right]{\lambda }^3+\frac{3}{2\lambda },$

$B=\frac{{\lambda }^3}{2}$

$C=\frac{{\eta }_0}{2},$     (12)

Where

$\lambda =\sqrt{\frac{1}{\alpha \sigma +\beta C_{1}s}},$

$C_1=\frac{\left(k-\frac{1}{2}\right)}{\left(k-\frac{3}{2}\right)},$  $C_2=\frac{(k-\frac{1}{2})(k+\frac{1}{2})}{2{(k-\frac{3}{2})}^2}.$  (13)

Here $\eta ={\epsilon }^{1/2}{\eta }_0$  where ${\eta }_0$  is the finite quantity of the order of unitary. On the other hand, if we assume the quasi-neutrality condition by employing the reductive perturbation method and using equations (4) -(5) and the Poisson's equation in form

$0=\alpha e^{\sigma \phi }-\beta {\left(1-\frac{s\phi }{k-3/2}\right)}^{-k+1/2}-n,$     (14)

one can drive the Burgers equation as follow:

$\frac{\partial }{\partial \tau }{\phi }_1+A{\phi }_1\frac{\partial }{\partial \xi }{\phi }_1+C\frac{{\partial }^2{\phi }_1}{\partial {\xi }^2}=0,$     (15)

Finally, we will obtain exact solution for ion acoustic shock waves in current plasma model by tanh method.^42,43 For K-dVB equation (11) a monotonic, kink-like shaped, solution is obtained via using this method in the form:

${\phi }_1=\frac{3C^2}{25AB}\left[4-{\left(1+tanh X\right)}^2\right],$     (16)

Where we have performed a transformation of the coordinates $X=k\left(\xi -V\tau \right);$ here $k=C/(10B)$ and $V=6C^2/(25B)$ are related to the inverse width and the speed of the shock, respectively.^42,43

In which for Burger equation (15) we have

$\phi 1=\phi m\left[1-tanh\left(\varsigma /\Delta \right)\right],$     (17)

where the amplitude $\phi m$ and the widthare given by

$\phi m=\frac{U}{A},$  and $\Delta =\frac{2C}{U}.$  (18)

(Here $\varsigma =k\left(\xi -U\tau \right),$  and $U=C^2/(5B)$ is a velocity [42-43].

In this study, a rigorous theoretical investigation of electrostatic shock structures in two electron temperature plasma (having cold and superthermal electron) with cold ions are carried out. By employing reductive perturbation method, K-dV Burgers equation is derived. It is found that the coefficients of the K-dVB equation are significantly modified by ratio of unperturbed density of hot electron to ion $\left(\beta =n_{h0}/n_{i0}\right),$ hot to cold electrontemperature ratio $\left(\tau =T_h/T_c\right)$ and superthermality parameter k. By assuming quasineutrality, Burgers equation is also derived and its details will be investigated in the following.

It should be noted that the nonlinear coefficienthave negative, zero and positive values. Therefore, it is observed that shock potential profiles are positive (negative) if $A>0\left(A<0\right).$ On the other hand, the vanishing of the nonlinear coefficient in Eqs. (11) and (15) (i.e., when) determines the critical values of $\beta ={\beta }_c.$ In continue, to find the parametric regimes for the existence of opposite polarity shock potential profiles, we have numerically analyzed the nonlinear A termand obtain $A=0\left(\beta versus \tau \right)$ curve in Figure 1. From this figure, it is clear that for the fixed values of $\tau =T_h/T_c=20$  and k=3 we have two critical values 0.812 and 0.976, where for densities lie in two ranges $0<\beta <{\beta }_{c1}\left(=0.812\right)$  and $0<\beta <{\beta }_{c2}\left(=0.976\right),$ the nonlinear coefficient is positive and we havecompressive shock waves, while the densities lie between these two critical values, namely ${\beta }_{c1}<\beta <{\beta }_{c2},$ lead to the rarefactive shock waves.

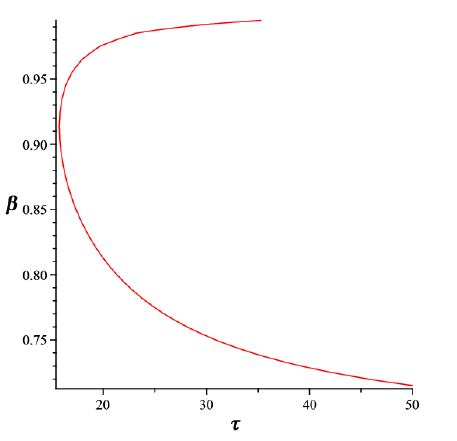
Figure 1 The showing variations of the nonlinear coefficient A = 0, the number density $\beta$ versus temperature $\tau$ for k = 3.

Potential profiles of the ion acoustic shock waves, as given by Eq. (16), for fixed values $\tau =20,k=3$ and different cases of density $\beta$ are investigated in Figure 2. It is observed that the amplitude of positive shock waves increases (decreases) with $\beta$ for case $0<\beta <{\beta }_{c1}\left(\beta <{\beta }_{c2}\right),$ (see Figure 2(a) and 2(c), respectively) in which for ${\beta }_{c1}<\beta <{\beta }_{c2}$ (rarefactive shock waves) the amplitude decreases by increasing the hot electron density see Figure 2(b). It should be remarked that our results are different from results given in.³⁶ They studied the influence of hot electron density population on shock waves and shown that there is only a critical value≈ 0.58 and in the both cases (compressive and rarefactive shock waves) the amplitude of shock increases with increase in the hot electron density.³⁷

Figure 2 Variation of ${\phi }_1$ with $\chi$ - Eq. (16) - for different values of $\beta$ with k=3, $\tau$ =20, and ${\eta }_0$ =0.3 for (a) 0 < $\beta$ < ${\beta }_{c1}$ (=0.812), (b) ${\beta }_{c1}$ < $\beta$ < ${\beta }_{c2}$ and (c) $\beta$ >${\beta }_{c2}$ (=0.976).

The hot to cold electron temperature ratio is examined in Figure 3. It is shown that for a fixed value of density $\beta =0.7$ (where it is assumed lower than first critical density ${\beta }_{c1})$ the amplitude of the shock waves increases as increases (see Figure 3(a)), while form Figure 3(b) it is found that for case $\beta =0.85$ (between two critical value) by increasing hot electron temperature, the amplitude of shock waves decreases. Finally, from Figure 3(c), it is clear that for case $\beta =0.985$ (bigger than second critical density ${\beta }_{c2})$ the amplitude increases as $\tau$ increases. This means with increase temperature the plasma model can support larger (smaller) compressive (rarefactive) shocks. On the other hand, withcomparing Figure 3(a) and 3(c), it is seen that the intensity of compressive shocks is significant when the plasma model satisfies higher density of hot electron. These results are important and don’t see in.³⁷

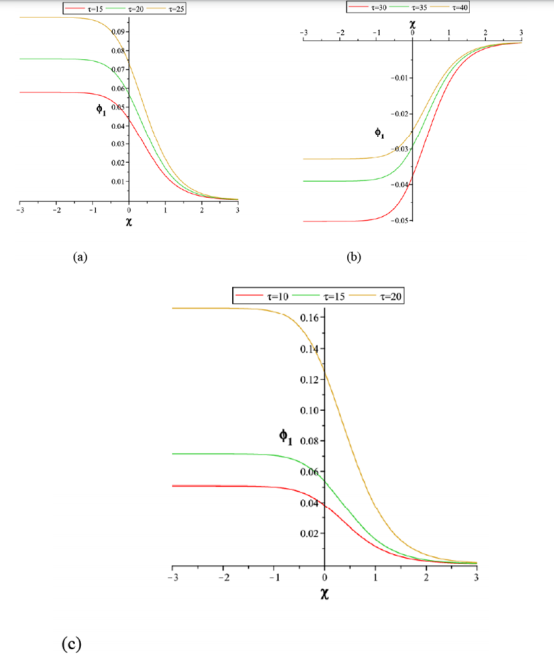
Figure 3 Variation of ${\phi }_1$ with $\chi$ - Eq. (16) - for different values $\tau$ with k = 3 and ${\eta }_0$ = 0.3for (a) $\beta$ = 0.7 (b) $\beta$ =0.85 and (c) $\beta$ =0.985.

It is clear that if dissipative effects (due to the kinematic viscosity) in a plasma medium become very strong the shock waves will appear instead solitons. Therefore, to complete discussion, the effect of kinematic viscosity is shown in Figure 4 for different density cases $(a) \beta =0.6, (b) \beta =0.85, and (c) \beta =0.995,$ respectively. It is observed that ion kinematic viscosity increases the amplitude both compressive and rarefactive shock waves. On the other hand, it is shown that shock strength increases as the viscosity in the system is increased. It is also clear that transformation from solitons profile to shock structure occur in large values ${\eta }_0.$ The results are similar to that obtained in³⁷ for an oblique propagation of shock wave in a superthermal magnetized plasma.

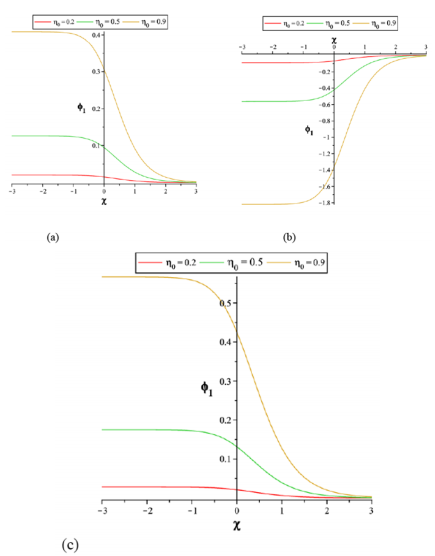
Figure 4 Variation of ${\phi }_1$ with $\chi$ - Eq. (16) - for different values of ${\eta }_0$ with k = 3 and $\tau$ =20 for (a) $\beta$ =0.6, (b) $\beta$ =0.85 and (c) $\beta$ =0.995.

In continue characteristics of the Burgers shock waves -described by Eq. (17) – is investigated. In Table 1, we give values of the amplitude $\phi m$  and width $\Delta$  shock waves for various values of density $\beta$  . It is seen that the amplitude of the compressive shock waves increases (decreases) as the density is lower (larger) than ${\beta }_{c1}\left({\beta }_{c2}\right),$  while the amplitude of the rarefactive shocks decreases by increasing density. In addition, it is interesting to note that the width of the shock waves seems to decreases with density $\beta$ for all cases of density.

The influence of hot electron temperature $\tau$ on the amplitude $\phi m$ and width $\Delta$ shockwaves – described by Burgers equation (17) – is examined in Table 2. This table show that as the hot to cold electron temperature ratio increases the amplitude of compressive shock waves increases. However, for the rare active shock, the amplitude of a shock decreases with increase in Also, it is clearly depicted that the considered plasma model support wider shocks as hot electron temperature increases. We have also investigated the effect of the kinematic viscosity on shock waves propagation in such plasma in Table 3. It is found that an increase in ${\eta }_0$  (meaning an increase in dissipation) considerably caused an increase in the amplitude both compressive and rarefactive shocks. On the other hand, it is found that shock strength increases as the viscosity in the system is increased. In addition, we see from Table 3, that shock waves have low width and propagated narrower for large kinematic viscosity coefficient.

We have investigated the nonlinear properties of shock waves in a nonlinear and dissipative media consisting of cold fluid ions and cold and hot (superthermal) electrons. Using the reductive perturbation method, the basic set of equations is reduced to K-dVB equation for lowest order perturbation. By assuming quasi-neutrality, Burgers equation is also derived. Exact stationary shock solution of the K-dVB and Burgers equations is presented through the tanh method [42-43] and the results obtained from present model can be summarized as follows:

1. The nonlinear term A is zero for some critical value of therefore shock waves with positive or negative amplitude can be found in present media.
2. Increase in hot electron to ion unperturbed number density ratio leads to the increase or decrease in the amplitude of shock waves. On the other hand, when the number density is lower than ${\beta }_{c1},$ the amplitude of shock waves increases, while it decreases for the number density larger than ${\beta }_{c1}$ in both cases positive and negative shock waves.
3. Increase in the ratio of the hot to cold electron temperature have also the significant effects on the amplitude of the shock waves.
4. An increase in the dissipation factor of the homogeneous plasma ${\eta }_0$ mediumleads to an increase the amplitude of shock waves.
5. Increase in the number density of hot electrons $\beta$ and the kinematic viscosity ${\eta }_0$ lead to decrease in the width of shock waves while increase in the temperature of hot electronleads to increase in the width of shock waves.

The findings of this investigation may be important in the laboratory and astrophysical/space plasma environments where two populations of electrons (cold and hot) and cold ions are present. In end, it should be mentioned that the effects warm ions, magnetic field and also the treatment of shock waves exactly in $\beta ={\beta }_c$ can be considered in such plasmas in future works.

None.

The author declares there is no conflict of interest.

None.

1. PG Drezin, RS Johnson. Solutions. Cambridge University press. 1989.
2. T Stix. Waves in plasmas. New York: American Institute of physics. 1992.
3. LD Faddeev, LA Takhtjan. Hamiltonian methods in the theory of solitons Springer –Verlage Berlin. 1980.
4. KG McClements, ME Dieckmann, A Ynnerman, et al. Surfatron and Stochastic Acceleration of Electrons at Supernova Remnant Shocks. Phys Rev Lett. 2001;87:255002.
5. SD Bale, MA Balikhin, TS Horbury, et al. The Microphysics of Collisionless Shocks a dissertation submitted to the faculty of the graduate school of the university of minnesota by lynn bruce wilson iii in partial  ulfillment of the requirements for the degree of doctor of PhilosophySpace Sci Rev. 2005;118:161.
6. E Lee, GK Parks, M Wilbr, et al. Nonlinear Development of Shocklike Structure in the Solar Wind. Phys Rev Lett. 2009;103:031101.
7. Y Nakamura, H Bailung, PK Shukla. Observation of Ion-Acoustic Shocks in a Dusty Plasma. Phys Rev Lett. 1999;83:1602.
8. Y Nakamura, H Bailung, Y Saitou. Observation of ion-acoustic shock waves undergoing Landau damping. Phys Plasmas. 2004;11:3925.
9. H Heinrich, SH Kim, RL Merlino. Laboratory Observations of Self-Excited Dust Acoustic Shocks. Phys Rev Lett. 2009;103:115002.
10. RB Spielman, JS De Groot, DA Rasmussen. An improved low‐pressure dc discharge. J Appl Phys. 1976;47:1909.
11. J Geiss, H Balsiger, P Eberhadt, et al. Investigation of Ion-Acoustic Solitons in Magnetosphere and Tokamak Warm Plasma with Two-Temperature Electrons. Space Sci Rev. 1978;22:537.
12. WD Jones, AL Lee, SM Gleman, et al. Effect of trapped electrons on soliton propagation in a plasma having a density gradient. Phys Rev Lett. 1975;35:1349.
13. MA Rehman, MK Mirsha. Ion-acoustic Gardner Solitons in electron-positron-ion plasmawith two-electron temperature distributions. Phys Plasmas. 2016;23:012302.
14. BN Goswaminm, B Buti. Large Mach number ion acoustic rarefactive solitary waves for a two electron temperature warm ion plasma. Phys Lett A. 1976;57:149.
15. M Tajiri, K Nishihara. Solitons and Shock Waves in Two-Electron-Temperature Plasmas. J Phys Soc Japan. 1984;54:572.  
16. B Buti. Ion-acoustic holes in a two-electron-temperature plasma. Phys Lett A. 1980;76:251.  
17. K Nishihara, M Tajiri. Solitons and Shock Waves in Two-Electron-Temperature Plasmas. J Phys Soc Japan. 1981;50:4047.
18. VM Vasyliunas. Low‐energy electrons on the day side of the magnetosphere. J Geophys Res. 1968;73:2839.
19. MP Leubner. A Nonextensive Entropy Approach to Kappa-Distributions. Astrophysics and space Sci. 2002;282:573–579.
20. V Pierrard, M Lazar. Kappa Distributions: Theory and Applications in Space Plasmas. Solar Phys. 2010;267:153–174.
21. MA Hellberg, RL Mace. Generalized plasma dispersion function for a plasma with a kappa-Maxwellian velocity distribution. Phys Plasmas. 2002;9:1495.
22. NS Saini, I  Kourakis, MA Hellberg. Electrostatic solitary waves in superthermal plasmas:an overview of recent results. Phys Plasmas. 2009;16:062903.
23. YD Jung, WP Hong. Ion acoustic solitons and supersolitons in a magnetized plasma with nonthermal hot electrons and Boltzmann cool electrons. Phys Plasmas. 2001;18:024502..
24. SH Chuang, LN Hau. Propagation of solitary waves in relativistic electron-positron-ion plasmas with kappa distributed electrons and positrons. Phys Plasmas. 2009;16:022901.
25. S Sultana, I Kourakis, NS Saini, et al. Oblique electrostatic excitations in a magnetized plasma in the presence of excess superthermal electrons. Phys Plasmas. 2010;17:032310.  
26. MP Leubner, N Schupfer. A universal mirror wave-mode threshold condition for non-thermalspace plasma environments. Nonlinear Processes Geophysics. 2002;9:75.
27. MP Leubner. Fundamental issues on kappa-distributions in space plasmas and interplanetary proton distributions. Phys Plasmas. 2004;11:1308.
28. TK Baluku, MA Hellberg. Ion acoustic solitons in a plasma with two-temperature kappa-distributed electrons. Phys Plasmas. 2012;19:012106.
29. M Shahmansouri, H Alinejad. Electrostatic wave structures in a magnetized superthermal plasma with two-temperature electrons. Phys Plasmas. 2013;20:082130.
30. F Verheest, MA Hellberg, I Kourakis. Electrostatic supersolitons and double layers at the acoustic speed. Phys Plasmas. 2013;20:082309.
31. S Sultana, G Sarri, I Kourakis. Ion acoustic shock waves in plasmas with warm ions and kappa distributed electrons and positrons. Phys Plasmas. 2012;19:012310.
32. HR Pakzad. The effect of q-distributed electrons on the head-on collision of ion acoustic solitary waves. Astrophys Space Sci. 2011;331:169.
33. M Mehdipoor. The characteristics of ion acoustic shock waves in non-Maxwellian plasmas with (G′/G)-expansion method. Astrophys Space Sci. 2011;338:1.
34. A Shah, S Mahmood, Q Haque. Positron-acoustic shock waves associated with cold viscous positron fluid in superthermal electron-positron-ion plasmas. Phys Plasmas. 2012;19:032302.
35. NS Saini, BS Chahal, AS Bains, et al. Zakharov-Kuznetsov equation in a magnetized plasma with two temperature superthermal electrons. Phys Plasmas. 2014;21:022114.
36. A Panwar, CM Ryu, AS Bains. Oblique ion-acoustic cnoidal waves in two temperature superthermal electrons magnetized plasma. Phys Plasmas. 2014;21:122105.
37. AS Bains, A Panwar, CM Ryu. Excitation and Formation Conditions of Monotonic Shock Waves in Magnetized Plasmas with Superthermality Distributed Electrons. Astrophys Space Sci. 2015;360:17.
38. MM Masud, M Asaduzzaman, AA Mamun. Cylindrical and spherical dust-acoustic Gardner solitons in dusty plasmas with nonthermal ions of distinct temperatures. Journal of Plasma Phys. 2012;79:2.
39. MS Alam, MM Masud, AA Mamun. Effects of bi-kappa distributed electrons on dust-ion-acoustic shock waves in dusty superthermal plasmas. Chinese Physics B. 2013;22(11):115202.
40. Effects of bi-kappa distributed electrons on dust-ion-acoustic shock waves in dusty superthermal plasmas. Chinese Phys. 2013;B22:115202.
41. Y Ghai, NS Saini. Low-frequency shock waves in a magnetized superthermal dusty plasma. Astrophys Space Sci. 2017;362:58.
42. T Taniuti, N Yajima J. Perturbation Method for a Nonlinear Wave Modulation. II. Math Phys. 1969;10:1369.  
43. W Maliet, W Hereman. The Tanh Method: Exact Solutions of Nonlinear Evolution and Wave Equations.Physica Scripta. 1996;54:563.
44. I Kourakis, S Sultana, F Verheest.  Note on the single-shock solutions of the Korteweg-de Vries-Burgers equation. Astrophys Space Sci. 2012;338:245–249.