I analyze the solution of the problem concerning ejection of charged particles from a sphere, outside which there is the Parker magnetic field. Depending on the magnetic field polarity, the particles escaping the sphere are shown to be either focused along the field symmetry axis, or drift from the axis along the equatorial plane. From this analysis, it follows that the obtained solutions may appear useful to understand the process of forming relativistic jets and disks observed in many space objects.

Keywords: astrophysics, relativistic jets and disks, magnetic field polarity, equatorial plane

Recently, astrophysicists have paid a special attention to such observational events in space as supernova, gamma-ray bursts (GRB), bursters, processes in active galactic nuclei (AGNs), quasars, etc. They are considered to emerge due to catastrophic processes in space, as a result of which a compact region forms, wherefrom a powerful electro-magnetic radiation emits, and fluxes of various energetic particles eject. We assume that the latter are cosmic rays (CRs). In this paper, I focus on the quasi-spherical region produced at the catastrophe site. This region is a source of relativistic and ultrarelativistic particles. This region existence time is determined by the processes occurring inside that may be either short-, or long-term. For example, to elucidate the formation of pulsing GRB,¹ the popular fireball model Piran2 is used. This model presupposes that there forms a compact ball (with the initial size of about 100 km) expanding at a relativistic velocity and comprising the quanta locked in it and electron-positron pairs. At an instant, quanta dramatically leave the ball thus forming a short gamma burst. Further, charged relativistic particles eject. They are accelerated in shocks (inner and outer) produced as a result of the ball shell "bloating" in a plasma medium at a near-light velocity, and of fast motion of substance in the ball.

Problem statement and input equations

In this study, I attempt to clarify to what consequences a CR ejection from an expanding spherical formation (that is assumed to form as a result of catastrophic phenomena in space) will lead. To describe the dynamics of high-energy particles ejected from the addressed shell, the following problem is stated. Let there be a sphere from which CR eject radially, and let there be space plasma and Parker magnetic field (further - Parker field). The Parker field is chosen on the grounds that for most stars, due to their rotation and emitting plasma wind from their surfaces, the structure of electromagnetic fields in their vicinity is similar to that inherent in the plasma heliosphere of the Sun.³ I term the electromagnetic field and plasma outside a star the heliosphere, whose spatial scale considerably surpasses the size of the sphere from which particles eject. I will use the terminology accepted in the solar heliosphere: if the magnetic field is directed away from the Sun in the Northern hemisphere, then it is positive; if the field is directed to the Sun surface in the same hemisphere, it is considered negative. In the cylindrical coordinate system $(r,z,j)$ that I use, the distance from the star will be designated through $R={\left(r^2+z^2\right)}^{1/2}(R>>r_{\odot }where{r}_{\odot }isthestarradius)$ . Then, the Parker electromagnetic field components in the heliosphere for the star magnetic field positive polarity takes the form:

$\begin{array}{l}{H}_{\phi }\left(r\right)=-H_{\odot }\Omega r{r}_{\odot }{}^2/(u{R}^2), \hfill \\ H_r\left(r\right)=H_{\odot }r{r}_{\odot }{}^2/R^3,\hfill \\ H_z\left(r,z\right)=H_{\odot }z{r}_{\odot }{}^2/R^3, \hfill \\ E_r{\left(r,z\right)}_{ }=-(\Omega r_{\odot }/c)rz{H}_{\odot }{r}_{\odot }/R^3,\hfill \\ E_z{\left(r\right)}_{ }=(\Omega r_{\odot }/c)r^2{H}_{\odot }{r}_{\odot }/R^3.\hfill \end{array}$    (1)

For the star magnetic field negative polarity, all the components are recorded with the reverse sign. Further, we assume that, by order of magnitude, $\Omega r_q\approx u,H_{\odot }{r}_{\odot }{}^2\approx H_o{r}_q{}^2$ , where $r_q$  is a characteristicdistance from the star, at which the radial and azimuthal components of the magnetic field are equal to each other: $H_r\left(r_q,0\right)=H_{\phi }\left(r_q,0\right)=H_o$ .

The goal of my study is to calculate the particle motion trajectories escaping from the sphere and further moving in the Parker field. I assume that the ejected particle density is much less than the density of plasma surrounding the sphere. Therefore, the particle dynamics may be considered in a one-particle approximation. I present the equations describing the particle motion in the Parker field (Formulas (1)) in the view

$\begin{array}{l}d(\gamma dr/dt)/dt=\gamma v_{\phi }{}^2/r+q{E}_r/m+q[H_z{v}_{\phi }-H_{\phi }{v}_z]/\left(mc\right),\hfill \\ d(\gamma r{v}_{\phi })/dt=qr[H_r{v}_z- H_z{v}_r]/\left(mc\right),\hfill \\ d(\gamma dz/dt)/dt=q{E}_z/m +q[H_r{v}_{\phi }{}_{ }- H_r{v}_{\phi }]/\left(mc\right), \hfill \\ m{c}^{2}d\gamma /dt=q(E_r{v}_r+E_z{v}_z).\hfill \end{array}$  (2)

Here, $q$, m are charge and rest mass of particles, velocity components $v_{\varphi }=rdj/dt,v_r=dr/dt,v_z=dz/dt,c$ is the speed of light, $\gamma ={[1-(v_{\phi }{}^2+v_r{}^2+v_z{}^2)/c^2]}^{-1/2}$ is the dimensionless energy normalized to the particle rest energy mc2. Due to the azimuthal symmetry, the generalized pulse moment persists:

$mgr{v}_{\phi }+q{A}_{\phi }r/c=Const,$

Where $A_{\phi }$ is the vector potential azimuthal component. As test particles, I address protons, for which the charge is equal to the electron charge, $q=е$ . Let us designate the radius of the sphere, from which protons eject, through $R_o$ . Then, let us introduce the dimensionless variables $\chi =r/R_o,x=z/R_o,\tau =\omega t,$ where $\omega =e{H}_o/mc$ , and designations $a=R_o/r_q,\beta =u/c,\lambda ={({\chi }^2+{\xi }^2)}^{1/2},\psi =d\phi /d\tau ,\epsilon =m{c}^2/\left(e{H}_o{R}_o\right)$ , by using which we obtain relations for accelerations along the axes r, φ, z

$\begin{array}{l}{d}^2\chi /d{\tau }^2=\chi {\psi }^2 +\xi \chi \psi /(\gamma a^2{\lambda }^3)+\chi d\xi /d\tau /(\gamma a{\lambda }^2)-(d\chi /d\tau ).(d\gamma /d\tau )/\gamma -\beta \epsilon \chi \xi /(\gamma a{\lambda }^3),\\ d^2\phi /d{\tau }^2=(\chi d\xi /d\tau -\xi d\chi /d\tau )/(\chi \gamma a^2{\lambda }^3)-2\psi (d\chi /d\tau )/\chi -\psi (d\gamma /d\tau )/\gamma ,\\ d^2\xi /d{\tau }^2=\beta \epsilon {\chi }^2/(\gamma a{\lambda }^3)-(d\xi /d\tau ).(d\gamma /d\tau )/\gamma -\chi (d\chi /d\tau )/(\gamma a{\lambda }^2)-{\chi }^2\psi /(\gamma a^2{\lambda }^3),\end{array}$

These equations were solved numerically at the following values of the parameters (characteristic of the Sun's heliosphere):

1. At the $r_q$ radius, the magnetic field value $H_o=2.2{10}^{–5}G,$
2. The relation of the star wind velocity to the speed of light β = u/c = 0.001.

Parameter $a$ varies within $10\le a\le 1000$ , parameter $\epsilon ={10}^{–}{}^2/a,$ the value of energy is confined to values $\gamma \le 10$ .

From the particle motion equations, one can see that the magnetic field value, $H_o$ , and the energy value, $\gamma$ , are included in the equations in the $\gamma /H_o$ combination. From this it follows that, at changes in values $H_o$ and $\gamma$ , the particle trajectories in the heliosphere calculated from the motion equations are identical as long as $\gamma$ and $H_o$ vary in such a manner that the $\gamma /H_o$  relation persists constants. I consider the addressed star to be similar to the Sun, but it may have other parameters (magnetic field, rotational speed, mass, radius, etc.). I assume that the values of the magnetic fields and of the proton energy are such that the Larmor radius of particles in the heliosphereismuch less than the characteristic size $r_q$ therefore, one may qualitatively analyze the proton motion in the heliosphere in the drift approximation. As known from the particle motion analysis in the solar heliosphere, particles in the Parker field experience two drift types: centrifugal and gradient, under whose effect particles eventually drift against the heliosphere electric field direction.

Considering the heliosphere axially symmetric relative to the axis around which the star rotates, and addressing the proton motion in the absence of collisions in the relativistic approximation, the equation set (2) closed form solution is presented in detail in (Kichigin 2014). All the particle dynamics regularities obtained from qualitative analysis in the positive and negative Parker field prove to be true in the numerical calculations below. The results of CR trajectory calculations are provided in the heliosphere meridional cut only in one quadrant of the Northern Hemisphere, because in all the adjacent quadrants the pattern of trajectories is reflection symmetric. In all the calculations, the correctness of calculations was tested through checking the values of the persisting values: total energy $([g+\beta \xi /(\lambda \alpha \epsilon )]=Const),$  and total momentum $([g{c}^2\psi –\xi /(\lambda {\alpha }^2)]=Const)$ . The accuracy of these values' persistence was not worse ${10}^{–11}$ . Figure 1 shows the 5-GeV CR trajectories for the magnetic field positive polarity. CRs radially escape from the sphere points with initial distances from axis $z {\chi }_0=r_o/R_o=0.01,0.1,0.3,0.5,0.7,$ parameter $a=100$ , and the initial coordinates along the z axis are determined from relations ${\xi }_0=z_{o/}{R}_o={(1–{\chi }_0{}^2)}^{1/2}$ . As it follows from Figure 1, all the particles escaping from the sphere drift towards the equatorial plane, reach the latter, and further drift along it moving away from the z axis.

Figure 1 Trajectories of the 5-GeV proton ejected from the sphere (dotted line) with the initial distances from the z axis ${\chi }_0=0.01,0.1,0.3,0.5,0.7$ indicated near the curves. Particles escape from the sphere, then, drifting along the arc, reach the equatorial plane, and further drift along this plane moving away from the z axis. Parameter $a=100$.

Figure 2 Trajectories of the 1.2-, 1.5- and 5-GeV protons ejected from the sphere with the initial distance from the z axisχ0 = 0.5 for the magnetic field negative polarity. The coordinates on the axes are presented in the logarithmic scale. Particles escape from the sphere, then they drift toward the z axis,and further move along this axis away from the equatorial plane. The population of the points belonging to the coordinates of the particle guiding centers is approximatedby the plot of the function z = Const r2 shown in Figure (solid line). Parameter $a=100$ . Figure 2 shows the trajectories of the 1.2-, 1.5- and 5-GeV protons ejected from the sphere with the initial distance from the z axis χ0 = 0.5 for the magnetic field negative polarity, with the coordinates on the axes presented in the logarithmic scale. As one can see in Figure 2, the particle departure of the particle guiding center from the z axis is low. Analyzing the calculation results shows that the particle guiding centers moving along the z axis form the surface, whose projection onto the quadrant is well approximated by the $z=Const{r}^2$ dependence shown in Figure 2 (solid line).

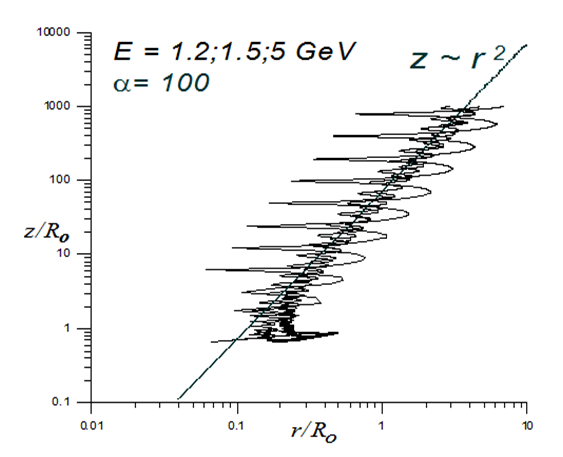
Figure 2 Trajectories of the 1.2-, 1.5- and 5-GeV protons ejected from the sphere with the initial distance from the z axis ${\chi }_0=0.5$ for the magnetic field negative polarity. The coordinates on the axes are presented in the logarithmic scale. Particles escape from the sphere, and then they drift toward the z axis,and further move along this axis away from the equatorial plane. The population of the points belonging to the coordinates of the particle guiding centers is approximatedby the plot of the function $z=Const{r}^2$ shown in Figure (solid line). Parameter $a=100$.

From the obtained analytical estimates in Kichigin⁴ and also from the results of the above numerical calculations, it follows that the Parker field possesses focusing properties, i.e., it play the role of a lens having the next properties plays: 1) the positive field collects all the energetic protons released radially from the sphere in the equatorial plane, 2) for the negative field, protons are focused in two thin rays with the divergence angle of several degrees that are directed away from the sphere along the field symmetry axis (star rotation axis). These properties of the Parker field have a satisfactory explanation, if one takes into account, that, eventually, in one case the particle drift leads to its moving into the equatorial plane, and, in the other, particles ejected from both Northern and Southern hemispheres further move away from the equatorial plane being close to the symmetry axis. In this paper, I generalize and develop the results of the analytical estimates obtained in Kichigin⁴ and the above numerical calculations. Let us start with analyzing the set of Equations (2) describing the particle dynamics in the Parker field. From the structure of the Equations (2), it follows that the particle trajectories calculated through these equations remain the same; even one interchanges simultaneously the particle charge signs and the electromagnetic field component signs in Equations (2). This implies that antiprotons (or electrons of the same energies) ejected from the sphere into the negative Parker field, eventually, (as well as protons ejected into the positive Parker field) will get to the equatorial plane scattering fanlike from the symmetry axis, thus forming a disk. Further, if one assumes that both positive and negative charged particles are simultaneously ejected from the sphere into the Parker field, then, eventually, for the positive field, protons will scatter fanlike along the equatorial plane moving away from the field symmetry axis, whereas antiprotons (and electrons of the same energies) will move away from the sphere along the field symmetry axis, thus forming two thin rays (jets).

All of these grounds allow me to formulate the principal result of this study: charged particles ejected radially from the sphere, outside which there is the Parker field are split by the field into two separate groups having different charge signs. One group moving away from the field symmetry axis will move in the equatorial plane. The other represents two thin rays of the particles moving away from the sphere along the field symmetry axis. Hence, it follows that, at radial ejection of particles from the sphere outside which there is the Parker field of any polarity, we will eventually see a pattern comprising two basic details: 1) two rays (jets) of the same-sign particles that moving away in two opposite directions from the sphere along the field symmetry axis, and 2) a disk (perpendicular to the field symmetry axis) formed by the opposite-sign particles that move along the disk withdrawing from the symmetry axis. The disk and jets are supposed to visually manifest themselves due to the emission of the electromagnetic waves excited by relativistic and ultrarelativistic charged particles in the presence of a magnetic field. One may assume that the addressed specific focusing properties of the Parker field may appear useful to understand the formation of relativistic jets and disks observed in the regions of the space where explosive phenomena occur. The study was performed with a support from the Program of the Presidium of the Russian Academy of Sciences No. 31 «High Energy Physics and Neutrino Astrophysics» within the «Cosmic Rays in Heliospheric Processes from Ground-based Observations» Project.

None.

1. Gehrels N, Ramirez-Ruiz E, Fox DB. Gamma-Ray Bursts in the Swift Era. Ann Rev Astron Astrophys. 2009;47(1):567–617.
2. Piran T. Gamma-ray bursts and the fireball model. Phys Rept. 1999;314:575–667.
3. Parker EN.Dynamics of the Interplanetary Gas and Magnetic Fields. ApJ. 1958;128:664.
4. Kichigin GN. Hydrodynamic instability and  spontaneous magnetic fields in a spherical laser plasma. Zh Êksp Teor Fiz.2014;119(4):657.