The process expressed by the term ‘magnetic reconnection’ or ‘annihilation’, which is supposed to produces the huge amounts of energy explosively under anti–parallel magnetic configurations, has long been considered as the sole process for solar flares. This paper consists of two parts. In the first part, after reviewing past magnetic reconnection studies, including four critical satellite observations, it is concluded that magnetic reconnection is not confirmed for solar flares in terms of the needed power and energy and that it is not the main process of flares. Thus, in the second part, it is demonstrated that solar flares must be powered by a photospheric dynamo, regardless of any theory. By introducing the concept of photospheric dynamo as the power supply process, solar flares are considered as a chain of process, which consists of a dynamo, currents/circuits to transmit the power/energy and energy dissipative processes manifested by solar flares—the electric current approach. It is shown that the photospheric dynamo process under a magnetic arcade can basically supply the power for two–ribbon Hα flares by its directly driven (the directly driven component DD) process. The energy for the explosive nature is accumulated by a photospheric dynamo in the dark filament above the magnetic arcade, which constitutes a current loop (the unloading component UL). In the current line approach, what we look for the explosive component is an electric current loop, instead of anti–parallel magnetic configurations.

Keywords: solar flares, auroral substorms, magnetic reconnection, electric current approach

The concept of magnetic reconnection under anti–parallel magnetic configurations has long been considered as the sole energy supply process for solar flares; for a comprehensive study of magnetic reconnection.^1,2 However, it is important to critically review its theories and observations. After the present review in Sections 1 and 2, it will be concluded in terms of power and energy that magnetic reconnection or annihilation is not confirmed for solar flares and perhaps is not responsible by itself for solar flares.

The concept of magnetic reconnection was born in solar physics in order to explain solar flares which are considered to be a sudden, explosive process with a large amount of energy (10³⁰–10³³ ergs) in a relatively short time. Since sunspots have strong magnetic fields, it was considered that magnetic energy is most likely the energy source. Kiepenheuer et al.,³ was perhaps one of the firsts to consider such a possibility. Since then, it has long been considered that the magnetic energy for solar flares is available and thus given as magnetic energy, so that the main concern in flare studies has been to find processes for an explosive conversion of given magnetic energy.

Actually, before Kiepenheuer’s suggestion, it was thought that the acceleration process of electrons is all that was needed to explain solar flares. Giovanellie et al.,⁴ may be the first to suggest an electrical discharge at neutral points to account for solar flares on the basis of his observations that solar flares tend to occur in complex sunspot groups, but the neutral point is the only location where electrons can be accelerated. Hoyle et al.,⁵ considered a neutral point discharge for the aurora, assuming that neutral point would form between magnetic fields carried by solar plasmas and the earth’s magnetic field.

Dungey et al.,⁶ formulated an electrical discharge theory in a ‘figure eight’ configuration of magnetic field. Cowing et al.,⁷ criticized those discharge theories by noting that the effects of induced currents are always to oppose the resulting change of the magnetic field (Lenz’s law).

Dungey et al.,⁸ responded to Cowling’s criticism by noting: “Certain other features of flares may be accounted for by the bulk motion resulting from a discharge at a neutral point. The effect of the discharge is to reconnect [italicized by the author] the lines of force at the neutral point, and this happens quickly.” This is perhaps the first time when the term “reconnect” was introduced in solar physics. On the other hand, in his book “Cosmic Electrodynamics”, Dungey et al.,⁹ repeated essentially the same description under the section titled “Discharges at neutral points” without mentioning the term magnetic reconnection. In fact, in his paper which is generally considered as the first paper on an open magnetosphere in magnetospheric physics, Dungey et al.,¹⁰ began his paper by stating” The discovery of a regular interplanetary magnetic field by Pioneer V has reawaked interest in Hoyle’s suggestion that the primary auroral particles are accelerated at neutral points in the combined field of an interplanetary field and the geomagnetic field”. He tried to explain auroral substorms in terms of the plasma convection (and the SD current; Chapman & Bartels¹¹ thus without considering magnetic reconnection or annihilation as it implies. Thus, at that point in time, it is not clear if he considered the process of converting accumulated magnetic energy for solar flares and the aurora.

Sweet et al.,¹² was the first to propose that an anti–parallel magnetic configuration may be necessary for the conversion of magnetic energy and suggested that such an anti–parallel magnetic field configuration can be produced, if two sunspot pairs collide; Figure 1A. Since then, magnetic reconnection has become the only candidate for the magnetic energy conversion for solar flares. As we discuss in Section 3, this conceptual collision process constitutes actually a photospheric dynamo as the power supply, so that the energy which is supposed to be released by magnetic reconnection must be supplied by a dynamo process, even if magnetic reconnection would work. Thus, it is not a complete theory.

Unfortunately, following Sweet’s theory, subsequent studies of solar flares have been based on pre–existing anti–parallel magnetic field configurations without considering how the anti–parallel configuration is produced (namely, the dynamo process of the initial collision of sunspot motions). Their main efforts have been how such a magnetic configuration can be annihilated spontaneously and suddenly. Aschwanden et al.,¹ Somov et al.,² and many others made comprehensive reviews of magnetic reconnection, but it is puzzling that their and many theoretical and observational studies have not made detailed estimates of the energy outputs resulting from magnetic reconnection.

Then, under the title “The solar–flare phenomenon and the theory of reconnection and annihilation of magnetic field”, Parker et al.,¹³ examined Sweet’s anti–parallel field conversion in terms of the resistivity, diffusion and other. He found that none of the known mechanisms is sufficiently rapid enough to account for solar flares. Thus, he concluded: “The observational and theoretical difficulties with the hypothesis of magnetic field annihilation suggest that other alternatives for the flare must be explored.” This problem may still exist, because many simulation studies of magnetic reconnection have to introduce an “effective resistivity” in order to overcome such a difficulty.

However, soon afterward, in his paper titled “Magnetic field annihilation”, Petschek et al.,¹⁴ pointed out that Parker overlooked standing magneto–hydrodynamic waves as a possible conversion of magnetic energy in an anti–parallel magnetic configuration and showed that magnetic energy can be rapidly converted into outward plasma flow energy for solar flares.

In the same year of the publication of Petschek’s paper Ness et al.,¹⁵ Discovered the magnetotail where magnetic field lines are nearly anti–parallel. In the same year, Akasofu et al.,¹⁶ published a paper on auroral substorms. Because of various morphological similarties between solar flares and auroral substorms, and because auroral substorms, which are, like solar flares, manifestations of electromagnetic energy dissipations associated with an explosive feature, many magnetospheric physicists have considered that auroral substorms are also caused by magnetic reconnection in the magnetotail.

Since then, Petschek’s theory of annihilation has become the basis of the present reconnection theories in both fields. In fact, it has been considered that magnetic reconnection under an anti–parallel condition is the only possible process of magnetic energy conversion and perhaps one of the most important processes in space physics. Indeed, Vasyliunas et al.,¹⁷ stated:”The process variously known as magnetic merging, magnetic field annihilation or magnetic reconnection (or re–connection) plays a crucial role in determining the most plausible, if not only, way of tapping the energy stored in the magnetic field in order to produce large dissipative events, such as solar flares and magnetospheric substorms”; note that he mentioned “tapping”, which implies tapping pre–existing energy.

On the other hand, Alfven et al.,^18–20 was very critical about the concept of magnetic reconnection. He noted²¹ “Hence in order to understand the properties of current–carrying plasma we must take account of the properties of the whole circuit in which the current flows. As this is not done in the magnetic merging [reconnection] theories, we conclude that they give a basically erroneous description of the phenomena….” What Alfven et al.,²¹ emphasizing is that plasma processes, such as solar flares, should be studied as a chain of power supply by a dynamo, currents/circuits and both phenomena as manifestations of dissipative process of the power/energy—the electric current approach. Thus, magnetic reconnection is not a complete theory for solar flares.

It is hoped that this lengthy introduction provides not only a history of the development of the concept of magnetic reconnection, but also some crucial problems related to it, which will be addressed in the following sections. In this paper, we take the electric current approach for the solar flares, instead of the magnetic field line approach. Thus, the major difference between the present work and theoretical studies in the past is that we pay attention to power/energy and also several crucial observational studies, which have been forgotten or dismissed, perhaps because they do not agree with reconnection theories. Since this approach has already been taken in studying auroral substorms, their results are often referred to where there are similar issues, although there is a difference of 10⁸ in terms of the power and energy between solar flares and auroral substorms.

Before discussing a photospheric dynamo as the power supply, it is necessary to point out that there are four important satellite observations which have unfortunately been forgotten or dismissed.

Four observations

1. In the summary statement of the Yohko Conference on Magnetic Reconnection in the Solar Atmosphere, Tsuneta et al.,²² noted:”There are ubiquitous neutral sheet structures with scale size—10³ km to several 10⁵ km almost everywhere on the Sun. It appears that most of these neutral sheet structures are static or dormant, and do not show explosive reconnection. Only the dynamically formed structure appears to have fast reconnection”. Thus, Tsuneta et al.,²² pointed out that magnetic reconnection is not spontaneous process, although many researchers are just satisfied by finding ant–parallel or the X–line structure in the solar atmosphere, and that there must be other crucial input processes which cause solar flares.
2. In another important observation, on the basis of X–ray observations of changing magnetic field configuration, Sheeley et al.,²³ noted:” these fields usually interact by changing their flux linkage, much as they do in a vacuum”. Further, Sheeley et al.,²⁴ observed: “reconnection occurs much more often than flares, thus usually occurs without them”. Thus, Sheeley et al.,²³ showed that their observations indicate that magnetic reconnection is not necessarily needed as the cause of solar flares.
3. Moore et al.,²⁵ examined six solar flares by Yohko (and Kitt Peak) observations in great details and concluded: “they show no evidence for reconnection between the exploding bipole and any surrounding magnetic fields.”Thus, both Sheeley et al.,²³ & Moore et al.,²⁵ pointed out that solar flares can occur without magnetic reconnection. Since they dealt with a number of flares, their examples are not likely to be exceptions.
4. One of the most accepted models of coronal magnetic reconnection was proposed by Hirayama et al.²⁶ His model and theories of reconnection require “compression” or plasma flow at the X–line; Figure 1B. However, Hudson & Khan²⁷ stated:”–––there is almost no evidence for inward flows”, indicating that there is no input. Since then, there was only one observation which specifically attempts to observe the inflow;²⁸ the inflow is supposed to be the most common feature for many magnetic reconnection theories.
5. The absence of the required inflow by many reconnection theories, if confirmed by most flares, indicates that the validity of reconnection theories is not confirmed by this observation, since Tsuneta et al.,²² and Sheeley et al.,²³ pointed out that magnetic reconnection should not be a spontaneous process.

Figure 1 (A) The formation of an anti–parallel magnetic configuration;¹² the two red arrows are added by the author. (B) Coronal model of solar flares by Hirayama et al.²⁶ In his model, the X–line and magnetic reconnection process occur above a magnetic arcade, not above sunspots. The magnetic arcade occurs along the neutral line between two unipolar magnetic regions of the opposite polarity. Magnetic reconnection is supposed to occur at the X–line.

These serious observations should not be dismissed, because they do not agree with reconnection theories.

Lack of the magnetic energy

Further, as mentioned earlier, in spite of a great emphasis of magnetic reconnection, there has been little effort in estimating the magnetic field intensity and the amount of available magnetic energy at the location where magnetic reconnection is supposed to occur. Priest et al.,²⁹ noted that B = 500 G. Even in a recent paper Shibata & Magara³⁰ noted B = 1000 G “in a typical sunspot”.

One of the most accepted models of magnetic reconnection was proposed by Hirayama et al.²⁶ Figure 1B. In Hirayama’s model, magnetic reconnection is supposed to occur above a magnetic arcade, not above sunspots. The magnetic arcade occurs along the neutral line between two unipolar regions of the opposite polarity. Magnetic reconnection is supposed to occur above the arcade, where it is indicated by the X–line formation. However, the intensity of the coronal magnetic field is not measurable at this time, so that there is no observational confirmation of the coronal model in term of energy. Thus, let us try to roughly estimate the magnetic energy where magnetic reconnection is supposed to occur above the magnetic arcade like Hirayama’s model. The width of the arcade is likely to be the distance of two–ribbon flares, namely 2.5 × 10⁴km (corresponding to the diameter of the earth). Assuming field intensity of as large as100 G at both sides of the neutral line (corresponding to B in the polar region of the earth), the field intensity at the top of the arcade (corresponding to the earth’s equator) will be about 100 G/2 = 50 G. Aschwanden et al.,¹ suggested that magnetic reconnection occurs above 4.4 × 10⁴km. Assuming the height to be 5 × 10⁴km, it is twice the height of the arcade, where an estimated B will be 50 G/2³ = 6.25G at that distance. Since the magnetic field there is not current free, let us assume B=10 G there, the corresponding minimum volume needed for weakest flares (10³⁰ ergs ÷ [B²/8π]) is a sphere of radius about 6 × 10⁴km, which seems to be too large even for the weakest flares, compared with the height of the arcade. Therefore, it is unlikely that the coronal magnetic field is capable of supplying the magnetic energy for solar flares.

In magnetospheric physics, the magnetic field intensity in the magnetotail has been observed repeatedly in the past, but the magnetic energy had not been estimated until Akasofu et al.,^31,32 pointed out that the magnetic energy between 10 Re (Re=the earth’ radius) and 20 Re in the magnetotail (where magnetic reconnection was reported to occur) is 6.5 x 10²¹ ergs (an over estimate), so that the magnetotail is incapable of providing the necessary energy by magnetic reconnection for the expansion phase (5x10²²–10²³ergs). In fact, the energy carried by plasma flows from the magnetotail, which is supposed to be the output of magnetic reconnection, is about 4.3 x 10²⁰ergs on the basis of the GEOTAIL satellite; it is far less than the amount of energy needed for the expansion phase of a medium intensity substorm. Thus, if auroral substorms were caused by magnetic reconnection of the accumulated magnetic energy in the magnetotail, a significant part of the magnetotail would be lost during auroral substorms, but the magnetotail is intact even during substorms.³³ Therefore, it may be concluded that magnetic reconnection, if it occurred, did not play the major role for auroral substorms.

It should be recalled that the magnetotail was the ground in proving theories of magnetic reconnection, because it is not possible to have in situ observations in the solar atmosphere. However, the magnetotail observations do not confirm theories of magnetic reconnection.³⁴ If it did occur in the magnetotail, the efficiency of magnetic reconnection is very low to be useful for auroral substorms.

Both theories and simulation studies of magnetic reconnection rely on “effective resistivity” which is most crucial in determining the efficiency of reconnection, but it has not been conclusively shown what it is and its quantity. Its quantity must be determined in situ in the magnetotail at this time, rather than adopting arbitrarily its quantity in order to reproduce observations in simulation studies. This problem may be related to Parker’s criticism mentioned in Section 1.

On the supporting observations

There are a large number of supporting observations on magnetic reconnection. Common to most of these observations and theoretical studies are:

1. They do not consider processes which led to anti–parallel configurations; solar flares must be powered. Before triggering anti–parallel magnetic configuration, the power is needed for any process related to energy production.
2. The magnetic energy around the location of the X–line is not estimated.
3. There is no definitive estimate of the energy produced by magnetic reconnection, so that it is not clear how much energy is generated around the X–line.

As mentioned already, many theoretical and observational studies on magnetic reconnection are not concerned with the above three points. As observational examples, Uchida et al.³⁵ & Su et al.³⁶ reported details of an interesting event by YOHKOH and SDO/AIA and RHESSI respectively, stating that they confirmed the occurrence of magnetic reconnection. However, unless the above three points can be clarified, it is not possible to definitively confirm theories of magnetic reconnection or the cause–effect relationship between events at the X–line and flare. Electrical discharges could occur around the X–line surrounded by plasmas as Dungey et al.,⁶ discussed, but it is not certain whether or not such a process around the X–line can provide the energy needed for solar flares.

Summary

In summary, it is concluded that the process expressed by the term ‘magnetic reconnection’ or ‘annihilation’, implying explosive production of the huge amounts of energy for solar flares in the corona by itself, is not confirmed and is perhaps not the main process of solar flares.

The formation of the X–line between two magnetic field lines without the huge amounts of magnetic energy conversion may now be called simply “connection”, as Tsuneta et al.,²² and Sheeley et al.,^23,24 showed; the X–line formation in vacuum is an example. In Section 4, we discuss such a case of connection, in which the X–line can be form without a vast magnetic energy conversion; this occurs in the formation of a current loop which is driven by a photospheric dynamo. For the above reasons, we propose in the following sections that a photospheric dynamo process can supply the needed power for Hα flares and can also accumulate and release the power in a current loop (the filament) for the explosive feature without reconnection.

The dynamo is absolutely needed for solar flares, regardless of any theory. The needed dynamo power for solar flares is defined by the Poynting flux P (erg/s) in terms of observable quantities^32,34 and is given by:

$P = {\displaystyle \int (E \times B)•dS = V\left(B^2/8\pi \right)S},$

where$V$ and$B$ are the speed of plasma flow and magnetic field intensity and$S$ is the front area of plasma flows; it is given by S= Ld, where L is the lateral length, and d the depth of the photosphere involved in the dynamo process (if needed, the volume is Vt, where t is the duration of flare); for simplicity, V is assumed to be perpendicular to B in the photosphere. The corresponding dissipation rate (erg/s) is denoted by$\delta$ (as a first approximation the Hα emission rate). In the past, Wilson et al.,³⁷ considers a photospheric dynamo around a cylindrical configuration, but did not estimate the energy involved.

Although we do not consider magnetic reconnection in the following sections, it may be worthwhile to demonstrate that the collision of two sunspot pairs considered by Sweet et al.,¹² in the first paper on magnetic reconnection for solar flares is actually a photospheric dynamo process. The reason for the following estimate is that a photospheric dynamo can generate the power needed for solar flares, not for supporting magnetic reconnection (or not for supporting Sweet’s theory). The power production is needed for solar flares for any theory of solar flares.

Let us first consider a very simple situation, in which a plasma flow with the lateral length L = 5 × 10⁴km approaches a magnetic field of intensity B =100G, with a speed V of 1km/s; the longitudinal length is given by Vt. In adopting the depth d, several measurements of plasma flows beneath active sunspot areas ($0.1 \sim 18 Mm$ ;$Mm = {10}^3 km$ ) are available,³⁸ and it is taken to be 1000 km, although there have been no such observations specifically associated with solar flares; the speed of plasma is observed to be up to$50 m/s \sim 1 km/s$ under active sunspots. This set of values (V, B, S) is quite reasonable for flare conditions and gives the power P = 2.0 × 10²⁶ erg/s, which corresponds to the minimum power (= the minimum flare energy [10³⁰ergs] divided by one hour), assuming that flares last for one hour. It is possible to obtain a higher power of 10²⁷ erg/s or more within the range of the above parameters.

Photospheric dynamo model Lee et al.,³⁹ Choe & Lee⁴¹ developed a photospheric dynamo model of solar flares. Its basis is a magnetic arcade, which is formed along the boundary (the neutral line) between two unipolar regions (where no sunspot pairs or sunspot groups are participating). Thus, their coronal magnetic configuration is basically the same as Hirayama’ model, except that there is a dynamo process under the magnetic arcade, not magnetic reconnection above the arcade. Figure 2A shows the geometry associate with the dynamo considered by Lee et al.,³⁹ Choe & Lee^40,41. Their model assumes an anti–parallel plasma flow (V = 2 km/s) along the centerline of arcade, which is the boundary (the neutral line) of two unipolar regions of opposite polarity, and magnetic field intensity B = 12 G (= 6 G + 6 G). These values are well within the observational constraints along the neutral line between two unipolar magnetic regions in a weakly active region.

In their model, as shown in Figure 2B, the field–aligned currents flow along the arcade magnetic field lines generated by this dynamo process. Thus, the arcade magnetic field lines constitute the circuit which transmits directly the dynamo power to the chromosphere for the ionization and dissipation, namely along the feet of the magnetic arcade for a two–ribbon Hα flare (one of the main dissipations).

Figure 2 (A) The geometry of the model of Lee et al.,³⁹ Choe & Lee⁴⁰. (B) The field–aligned currents along the magnetic arcade (Courtesy of G. S. Choe). (C) A simplest type of flares, called spotless flares⁴³ and a simulation of a line current by Choe & Lee⁴⁰.

In the model, the intensity of the field–aligned current is approximately 10^–4A/m² (Figure 2B), corresponding to the total current and power carried by the electrons are respectively about 10¹² A and 10²⁵ erg/s assuming the cororal electron are accelerated to 100 keV); the upward current is carried by downward streaming electrons, so that there are two ribbons of the Hα emissions along the feet of the magnetic arcade.⁴² Large Ha flares are associated with energy of about 10²⁶erg/s.⁴³ Thus, the photospheric dynamo model by Choe and Lee under the above conditions can provide the power dissipation (the two–ribbon Hα emission) for simplest and weakest flares, namely at least for spotless flares (Figure 2C).

Spotless flares do not require the presence of sunspots. As mentioned in Section 2, since magnetic reconnection is unlikely to play the role, spotless flares can be produced directly by a photospheric dynamo process. Thus, we consider that spotless two–ribbon flares are the direct effect of basic the dynamo process, namely the directly driven (DD) process by the dynamo, so that they are one of the two basic elements of solar flares.

There should be the minimum power for solar activities to be recognized as flares, together with typical features. In auroral substorms, the minimum power is about 10¹⁸erg/s (corresponding to the geomagnetic AE index above zero, and a sudden brightening of an arc; other activities are called pseudo–breakup). So far, there is no such a study for solar flares, so that it is appropriate to consider the minimum power to be about 2.0x 10²⁶erg/s (=the minimum flare energy 10³⁰ergs divided by one hour). Therefore, it may be said that there is no flares in the quiet sun.

It is well–established that two–ribbon flares occur also along the neutral line in an active sunspot group. Since the dynamo power is proportional to B², active regions provide generally higher powers than less active regions. This is one of the reasons why solar flares are generally associated with regions around sunspots.

Since the concept of a dynamo process is introduced in studying solar flares in this paper, it is crucial to distinguish the directly driven (DD) component by the dynamo and the component which results from unloading (UL) of the accumulated energy for the explosive process. What we observe is (DD+UL). It may be worthwhile to know how they are separated for auroral substorms, together with some results.

Auroral substorms consist of three phase, the growth, expansion and recovery phases; the explosive feature occurs during the expansion phase. For auroral substorms, in which V and B are the solar wind speed and the intensity of the interplanetary magnetic field (IMF) respectively; the solar wind speed V varies from 300 km/s to more than 1000 km/s, while the magnetic field intensity B varies from about less than 5 nT to more than 25 nT. The area is given by$S=si{n}^4\left(\theta /2\right)l^2$ where$\theta$ is the polar angle of the IMF and l is 5 Re (Re = the earth’s radius); the dissipation rate δ is mainly the Joule heat production rate in the polar ionosphere. For V= 500km/s, B= 5nT, the maximum power is P= 3x10¹⁹erg/s.

In auroral substorms, this separation was accomplished quantitatively by the fact that the DD and UL components have different current systems in the ionosphere; the DD component has a two–cell current system, while the UL component has a single cell current system (Figure 3).⁴⁴

Figure 3 shows the relationship among$\epsilon \left(=P/8\pi \right)$ , DD and UL. It is found that$P\left(t\right)>>\delta \left(t\right)$ during the growth phase which lasts for about one hour before the expansion phase; it is this growth phase which enables the magnetosphere to accumulate the magnetic energy.$P\left(t\right)$ is about 5x 10¹⁸erg/s, but the dissipation rate$\delta \left(t\right)$ is very small during the growth phase because the ionization in the ionosphere is very weak to conduct electric currents before the expansion phase. Thus, it is found that the power is accumulated as magnetic energy, at most 10²³ergs for a medium substorm [AE= 1000 nT]) in the inductive circuit of the magnetosphere, mostly within a distance 10 Re (Re= the earth’s radius), not in the magnetotail.

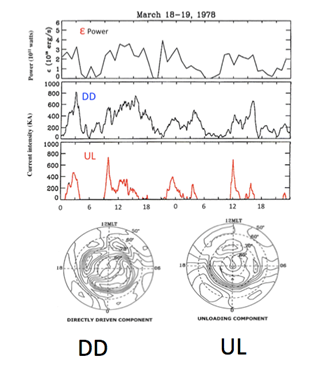
Figure 3 The relationship among the power (= ε), the DD and UL components for substorms. Both the DD and UL current systems are shown at the bottom. The DD current follows roughly ε. The UL current occurs impulsive and short–lived.

It can be seen that the DD component is roughly (within the accuracy of observations) follow the power$\epsilon \text{ =}\left(P/8\pi \right)$ . On the other hand, the UL component is impulsive or explosive and short–lived. It is the UL component which is produced by conversion of magnetic energy which is accumulated during the growth phase and which causes impulsive (explosive) auroral activities, namely the expansion phase of auroral substorms.

For solar flares, since we have so far no quantitative way to distinguish the DD and UL components, we attempt to distinguish them here in terms of observed phenomena:

1. Spotless flares as the directly driven component (DD)

As mentioned in Section 4(a), we identify spotless flares as a result of the directly driven (DD) component.

2. Explosive process produced by the UL component

The current line approach looks for current loops which have enough magnetic energy, instead of anti–parallel magnetic configuration. We identify that magnetic energy in the current loop associated with the dark filament is responsible for the UL (explosive) component, as suggested by Alfven & Carlqvist⁴⁵ instead of anti–parallel magnetic configurations (Figure 4C).

It is well–known that the dark filament between two ribbons of the Hα emission disappears at about time of flare onset. This phenomenon of a sudden disappearance of the dark filament was described in detail by Svestka et al.⁴³

In Figure 4A, an example of the disappearance of the dark filament at about the time of flare onset. This is the well–known feature at about the time of the explosive onset, although it is not received much attention in recent years, except by Moore et al.²⁵ when the rising filament is seen beyond the photosphere, it is seen as a bright erupting prominence. In the upper part, a weak Hα emission is recognizable, which might correspond to an auroral arc before expansion phase onset.

It is known that currents flow in the dark filament above the magnetic arcade (Figure 5).⁴⁶ Choe & Lee^40,41 showed by the same simulation that a current loop is also formed above the magnetic arcade by the same dynamo process. This process is not the huge energy release process and is ‘connection’, as defined and described at the end of Section 2. This is a part of the chain of processes driven by the photospheric dynamo. In this paper, we suggest that the dynamo–driven current loop has magnetic energy which is sufficient for the explosive process.⁴⁵

Figure 4 (A) An example of the disappearance of the dark filament at about the time of flare onset. Two typical solar flares. (The Hida Observatory, courtesy of E. Hiei). (B) The formation of a current loop above the arcade.^40,41 (C) The current loop suggested by Alfven & Carlqvist⁴⁵.

Figure 5 (A) Magnetic fields associated with the currents in the filament above magnetic arcades.⁴⁶ (B) The magnetic fields in the filament for launching a coronal mass ejection (CME).⁴⁷

Magnetic energy W in a current loop is given by:

$W=\left(1/2\right)J^{2}L,$

where$L$ denotes the inductance in the loop circuit an$J$ is the current intensity. Chen & Krall⁴⁷ estimated the intensity of their loop current to be 10¹A in their theory of CMEs. For medium flares (10³²ergs),$L$ is estimated to be 2000 H; Alfven et al.,⁴⁸ estimated the inductance of similar current to be 500 H.

The unloaded (released) magnetic energy is expected to enhance further the Hα emission (flare onset as seen in Figure 3A) and cause CMEs and other flare activities. The unloading (releasing) process of the magnetic energy in the current loop must be caused by disruption of the current loop. Alfven et al.,¹⁹ suggested the formation of a double layer as the cause, but it may be other possibilities, such as current instabilities. However, how the current loop is disrupted and how the unloaded energy produces the explosive phenomena, including the enhancement of the Hα emission, are beyond the scope of this paper. In this respect, it is interesting to note that Kurokawa et al.,⁴⁹ showed that exploding prominence (filament) has a rewinding motion, indicating a reduction of the current in prominences.

Since the concept of magnetic reconnection has prevailed for a long time without much criticism in the past, it is an appropriate time to review it from the fundamental point of view that solar flares are mostly various manifestations of electromagnetic dissipation processes and that any theory of solar flares requires the power. We have taken the current line approach for solar flares, instead of the magnetic field line approach.

It is shown that the current line approach provides a different view of solar flares from the magnetic field line approach. It is worthwhile to study solar flares by both the current line approach and the magnetic field line approach. This is because curl B = i.

This approach considered that solar flares must be powered by a dynamo process, a photospheric dynamo. Consequently, this approach also considers that solar flares should be discussed in terms of the directly driven component by the dynamo (DD) and the explosive component (UL) resulting from a sudden release of magnetic energy. It is shown that the photospheric dynamo can supply the power/energy for the two–ribbon Hα emission (the DD component) and the current loop (the UL component). The current line approach identifies the dark filament and associated current loop as the location, in which the magnetic energy is accumulated for the explosive process, instead of antiparallel magnetic configurations.

Further, when we consider the total input–output (power–dissipation) relationship throughout the life time of a solar flare, we can estimate that the input–output relationship is given by${\displaystyle \int P\left(t\right)dt}={\displaystyle \int \delta \left(t\right)dt}$ , (where$\delta$ denotes the energy dissipation rate), so that there is no major extra hidden energy, such as the annihilation of the pre–existing anti–parallel field; the same is shown on auroral substorms.^50,51

The author would like to thank Drs. Drs. L. C. Lee and G. S. Choe for their discussions on their model of solar flares. He acknowledges also the reviewer of the earlier manuscript for his detailed comments.

Author declares there is no conflict of interest.

1. Asschwanden M. Physics of the Solar Corona: An Introduction. Germany: Springer; 2005. p. 842.
2. Somov BV. Plasma Astrophysics. Germany: Springer; 2012.
3. Kiepenheuer KO. Solar activity. In: Kuiper GP, editor. USA: University of Chicago Press; 1953. p. 322–463.
4. Giovanelli RG. Magnetic and electric phenomena in the sun’s atmosphere associated with sunspots. Monthly Notices of the Royal Astronomical Society.1947;107:338–355.
5. Hoyle F. Some Recent Researches in Solar Physics. UK: Cambridge University Press; 1949.
6. Dungey JM. LXXVI: Conditions for the occurrence of electrical discharges in astrophysical systems. Philosophical Magazine. 1952;44(354):725–738.
7. Cowling TG. Solar electrodynamics. England: The Sun News Paper; 1953. p. 532–591.
8. Dungey JM. The neutral point discharge theory of solar flares. A reply to Cowling’s criticism. In: Lehnert B, editor. Electromagnetic Phenomena in cosmical Physics, Proceedings IAU Symposium, no.6, UK: Cambridge University Press; 1958. p. 135–140.
9. Dungey JM. Cosmic Electrodynamics. UK: Cambridge University Press; 1958.
10. Dungey JM. Interplanetary magnetic field and the auroral zones. Physical Review Letters. 1961;6(2):47–48.
11. Chapman S, Bartels J. Geomagnetism. UK: Oxford University Press; 1940.
12. Sweet PA. The neutral point theory of solar flares. In: Lehnert B, editor. UK: Electromagnetic Phenomena Cosmical Physics, Cambridge University Press; 1958. p. 123–134.
13. Parker EN. The solar–flare phenomenon and the theory of reconnection and annihilation of magnetic field. Astrophysical Journal Supplement. 1963;8:177–184.
14. Petschek HE. Magnetic field annihilation. In: Hess WH, editor. The Physics of Solar Flares, Proceedings of the AAS–NASA Symposium held 28–30 October 1963, at the Goddard Space Flight Center, Greenbelt, MD. USA: NASA, Science and Technical Information Division; 1964. p. 425–439.
15. Ness NF, Scearce CS, Seek JB. Initial results of the Imp 1 magnetic field experiment. Journal of Geophysical Research. 1964;69:3531–3569.
16. Akasofu SI. The development of the auroral substorm. Planetary and Space Science. 1964;12(4):273–282.
17. Vasyliunas VM. Theoreticalmodels of magnetic field merging. Reviews of Geophysics. 1975;13(1):303–336.
18. Alfven H. Electric currents in cosmic plasmas. Reviews of Geophysics. 1977;15(3):272–284.
19. Alfven H. Cosmic Plasma. Germany: Springer; 1981.
20. Alfven H. Double layers and circuits in astrophysics. IEEE Transaction on Plasma Science. 198614(6):779–793.
21. Alfven H. The second approach to cosmical electrodynamics. In: Egeland A & Holtet J, editors. The Birkeland Symposium on Auroras and Magnetic storms. France: Centre National de la Recherche Scientifique; 1967. p. 439–444.
22. Tsuneta S. Magnetic reconnection: Open issues. In: Bentley RD & Masiska JT, editors. Magnetic reconnection in the Solar Atmosphere. USA: ASP Conference series; 1996. p. 409–418.
23. Sheeley NR. Energy released by the interaction of coronal magnetic fields. Solar Physics. 1976;47(1):173–180.
24. Sheeley NR, Bohlin JD, Brueckner GE, et al. XUV observations of coronal magnetic fields. Solar Physics. 1975;40(1):103–121.
25. Moore RL, Steering AC, Hudson HS, et al. Onset of the Magnetic Explosion in Solar Flares and Coronal Mass Ejections. The Astrophysical Journal. 2001;552(2):833–848.
26. Hirayama T. Theoretical model of flares and prominences:1. Evaporation flare model. Solar Physics. 1974;34(2):323–338.
27. Hudson HS, Khan JI. Observational problems for flare models based on large–scale magnetic reconnection. In: Bentley RD & Mariska JR, editors. USA: ASP Conference Series; 1996:135–144.
28. Yokoyama T, Akita K, Morimoto T, et al. Clear evidence of reconnection inflow of a solar flare. The Astrophysical Journal. 2001;546:L69–L72.
29. Priest ER. Solar Flare Magnetohydrodynamics. The fluid mechanics of astrophysics and geophysics. USA: Gordon and Breach Science Publishers; 1981.
30. Shibata K, Magara T. Solar flares: Magnetohydrodynamic processes. Living Reviews in Solar Physics. 2011;8:1–99.
31. Akasofu SI. Where is the magnetic energy for the expansion phase of auroral substorms accumulated? Journal of Geophysical Research. 2013;118(11):7219–7225.
32. Akasofu SI. Where is the magnetic energy for the expansion phase of auroral substorms accumulated ?:II. The main body, not the magneyotail. Journal of Geophysical Research. 2017;112(8):8479–8487.
33. Angelopoulos V, McFadden JP, Larson D, et al. Tail reconnection triggering substorm onset. Science. 2008;321(5891):931–935.
34. Akasofu, SI. Auroral substorms: Search for processes causing the expansion phase in terms of the electric current approach. Space Science Reviews. 2017;212(1–2):341–381.
35. Uchida Y, Hirose S, Yamaguchi T, et al. Observations of flares and active regions from YOHKOH, and magnetohydrodynamic models explaining them. Astrophysics and Space Science. 1999:145–169.
36. Su Y, Veronig AM, Holman GD, et al. Imagimg coronal magnetic–field reconnection in a solar flare. Nature physics. 2013;9:489–493.
37. Wilson PR. The possibility of a photospheric dynamo. Australian Journal of Physics. 2006;38:911–918.
38. Kosovovichev AG, Duvall TL. Investigation of a sunspot complex by time–distance helioseismology. In: Chodhary PD, Strassmeter KG, editors. The Physics of the Sun and Star Spots. Germany: Proceedings IAU Symposium; 2010.
39. Lee LC, Choe CS, Akasofu SI. A simulation study of the formation of solar promineneces. Space Plasma: Coupling between Small and Medium Scale Processes. 1995;86:29–42.
40. Choe GS, Lee LC. Evolution of solar magnetic arches, I. Ideal MHD evolution under footpoint shearing. The Astrophysical Journal. 1996;472:360–388.
41. Choe GS, Lee LC. Evolution of magnetic arcades, II. Effects of resistivity and solareruptive processes. The Astrophysical Journal. 1996;472:372–388.
42. Haerendel G. Solar auroras. The Astrophysical Journal. 2012;749:1–13.
43. Svestka Z. Solar Flares. Netherlands: D Reidel Publishing Company; 1976.
44. Sun W, Xu SY, Akasofu SI. Mathematical separation of directly–driven and unloading components in the ionospheric equivalent current during substorm. Journal of Geophysical Research. 2000;103(A6):11695–11700.
45. Alfven H, Carlqvist P. Current in the solar atmosphere and a theory of solar flares. Solar Physics. 1967;1(2):220–228.
46. Bothmer V, Schwenn R. Eruptive prominences of magnetic clouds in the solar wind. Space Science Reviews. 1994;70(1–2):215–220.
47. Chen J, Krall J. Acceleration of coronal mass ejection. Journal of Geophysical Research. 2003;108(A11):1–22.
48. Alfven H. Cosmical Electrodynamics. UK: Oxford University Press; 1950.
49. Kurokawa H, Hanaoka Y, Shibata K, et al. Rotating eruption of untwisting filament triggered by the 3B flare of 25 April, 1984. Solar Physics. 1987;108(2):251–264.
50. Akasofu S. Physics of Magnetospheric Substorms. Netherlands: D Reidel Publishing Company; 1977. p. 599.
51. Kiepenheuer KO. Solar activity. In: Kuiper GP, editor. USA: University of Chicago Press; 1953. p. 322–463.