Empirical data for all planets in the solar system were analyzed to determine the kinetic, potential, and total energy of each, as well as the area each sweep out per second. As expected, it is the conservation of angular momentum, and not the conservation of energy, that ensures planets sweep out equal areas in equal times through any orbit region. Planets all follow the Second Fundamental Theorem of the Calculus while orbiting, where swept area increases progressively as a function of distance from the sun. The potential energy for each is twice the kinetic energy which is consistent with theoretic explanation. The Universal Gravitation constant G for a quantity of mass is not altered by huge changes in planet temperatures which clarify a property of gravity. Unique features of the planetary orbits further expand the Newton explanation that the system behaves as a vast wound clock, rather than a random assemblage of planets.

Keywords: solar system, planet, kinetic energy, wound clock, gravity, orbit radius, velocity, sweep arc

The system of planets orbiting the sun trace planar elliptic travel paths of varying speed but with constant swept area in a given time in any orbit region.¹ This was first observed empirically by Johannes Kepler (1609–1619) from detailed telescopic data of continuously changing planet positions over time. The mechanism by which invisible gravitational force fields, which emanate from the sun and the planets to tether planets in orbits on the solar ecliptic, was demonstrated mathematically by Isaac Newton after the discovery of the Fundamental Theorems of the Calculus(1665). Each planet in its orbit travels at a proper velocity at a given radius r, not too fast so as to prevent escape for the sun’s gravity, and not too slow so as to prevent collapse into the sun.

We here analyze solar system data, comparing for all planets the average kinetic energy, potential energy, orbit radius, velocity, and area swept out per second, to help explain the basis for the dynamic nature of orbits.

Using widely–published data for planet average velocities and average orbit radii,² the area swept out per second for all planets is plotted as a function of distance from the sun and shows a smooth relationship (Figure 1). No smooth relation exists between kinetic energy, removal potential energy, or total energy, which are scalar quantities, not directional vector quantities, vs r. As r increases, velocity progressively decreases as the square root of r, so the area among the planets shows a smooth trend modeled with a quadratic equation with high R².correlation.

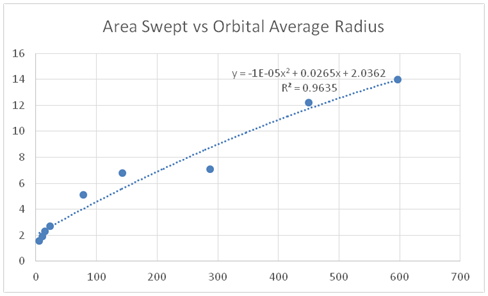
Figure 1 The area traced out by planets in one second of travel time (m² x 10¹⁵), plotted as a function of average radius from the sun (m x 10¹⁰). The area swept out by the planets matches the order in the solar system in distance from the sun, as shown for mercury, venus, earth, mars, jupiter, saturn, uranus, neptune, and pluto.

The distance from the sun to earth at aphelion is larger than the distance from the sun to earth at perihelion. Thus, the area swept out by earth radii from the sun for a given arc length segment s at aphelion would be large compared to the area swept out for the same arc length s at perihelion. So, to sweep out equal areas in a given time, it is necessary for the earth to travel faster at perihelion than at aphelion. This is borne out by observation, where the speed of the earth varies from 67,700 to 65,500mph (30.3–29.3km/s) at these positions, as the radii vary from 147.1 x 10⁹m to 152.1 x 10⁹m. As expected from Kepler’s law, the angular momentum multiple rv from the observed planetary data is constant within observational error (due to gravitational forces from other planets and other possible factors).

The Second Fundamental Theorem of the Calculus states that any smooth continuous function is the derivative of its own integral. Thus, the ordinal value of any function equals in magnitude the rate at which the integral area is traced out by that function at any position along its domain. The salient feature of solar system dynamics that follows the Fundamental Theorems of the Calculus is that the area swept out by any planet a particular distance from the sun must always change at a rate determined by the ellipse function itself. This is because the rate of change, or the derivative, of the area integral of any function is given by the magnitude of the function itself at any position, regardless of the shape of the function. Since the equation for an ellipse is $x^2/a^2+y^2/b^2=1$ , where a and b are the perpendicular axes through the center of the ellipse, and for the earth ab = 2.2 x10²² m², then the area computed by integrating the equation for a small displacement should equal the ordinal value of the function itself multiplied by the length ds of the corresponding arc segment. In Calculus notation, dA/dx (rate that area changes) = f (any function that sweeps out an area), so dA (an area increment) = fdx (multiple of the ordinal function value times a miniscule shift width).

Since the difference between the center of the elliptic plane and the position of the sun at a focus (2.5 x 106 km) is miniscule compared to the radial distance of the planets, it is possible to verify how planets follow the Second Fundamental Theorem. The integral of the equation for the ellipse, after trigonometric substitution where $x=r\cos \theta$  and$y=r\sin \theta$ , is$\left(b/a\right){\displaystyle \int a^{2}si{n}^2\theta d\theta =ab\left[\left(1/2\right)\theta –\left(1/4\right)sin\left(2\theta \right)\right]}$ , which may be evaluated for any change in$\theta$ sweep angle desired. From the Second Fundamental Theorem, the derivative of the area integral must be the ordinal value of the original function itself at any position. For a miniscule shift in time and$\theta$ and approximating the ellipse equation as that of a great circle with radius r, the ordinal value of the function centered so that the region at which the average radius is on the ordinal axis directly above the origin, equals the rate of change of area of the integral function, which here is y = r. If large sweep angles are used, then the computed values for the two methods are inaccurate because the integral is the exact area between two ellipse positions along the horizontal axis if velocity did not vary with time, but it does. Also, the two methods would deviate from each other because the ordinal value of the ellipse, at one value of r, times the sweep distance, represents Cartesian area between the horizontal axis and a single value of r which varies with orbit position. If an infinitesimal sweep time is used, then the two methods for computing area increments yield equal values.

Using an arbitrary small sweep travel time of 12 microseconds, the average velocity of the earth multiplied by this time is a sweep arc of s = vt = (28,000m/s)(12 x 10^–6sec) = 0.336 meters. Since $s=r\theta$ for any circle arc may be employed for such a small shift angle, this is an angle of s/r = 0.336/149x10⁹ = 2.2 x 10^–12 radians. Integrating the ellipse equation from $\theta =0to2.2x{10}^{-12}$ radians produces an area A = 2.2 x 10²²{(1/2)2.2x10^–12 – (1/4)sin[2(2.2x10^–12)]} = 2.42 x 10¹⁰ square meters. In good agreement, the average radius of the earth (which is the ordinal value of the ellipse equation where the tangential velocity is perpendicular to the horizontal axis such as at perihelion or aphelion depending on orientation of the ellipse, here being the average r) multiplied by the average horizontal width from the sweep arc s is (1/2)rs = 149 x 109 x (1/2)0.336 = 2.50 x 10¹⁰ square meters. The desired area segment is not the rectangle along the horizontal axis, so each was multiplied by (1/2) for the segment traced out from the origin.

To correct for the fact that what is desired is the area swept out by a ray extending from the focus or center of mass barycenter along the ellipse, rather than the ellipse center, the integral of the polar form of the ellipse equation, $r=ed/\left(1+esin\theta \right)$  is used. Area is computed from ${\displaystyle \int \left(1/2\right)r^{2}d\theta }$ ,3 where e is the eccentricity of the orbit (for earth e = a/c = 0.01667 since c = 2.4 x 109m, and d = a2/c – c = 8.8 x 1012m). This produces an area for this sweep angle of A = 2.46 x 1010square meters.¹ Here, the swept area is that exactly traced by a ray from the sun at the focus of the ellipse, rather than from the mathematic center of the ellipse. This indicates that the computed area from the Cartesian formula which does not correct for the distance off–center of the ellipse at which the sun sits at a focus is not significantly different that the exact area from the polar formula. Indeed, the 2.5 x 10⁶km distance from the sun, at the ellipse focus, to the center of the ellipse, is only 0.001% of the average earth–sun radial distance r so the Cartesian formula. Again, from the Second Fundamental Theorem, the area may be computed without actually requiring integration of the function$\left(1/2\right)r^2\theta$ , as long as the sweep angle is small, as used here. Thus, $A=\left(1/2\right)r^{2}d\theta ={\left(149x{10}^9\right)}^2\left(2.2x{10}^{-12}\right)=2.44x{10}^{10}$ square meters, as before. Although Newton used Cartesian graphed functions in discovering the Calculus, notice that the polar equation also follows the Second Fundamental Theorem. Every function sweeps out an area from the horizon, which is computed with its integral in square measure, and, as a derivative of its integral, must have ordinal values in linear measure that equal the magnitude of the rate that area is swept out by the function.

Taken together, this demonstrates that planets travel in their elliptic orbits while sweeping out an area at a rate determined by the orbit radius itself at any position, where the radius determines the gravitational flux and thus orbit velocity at any position, so that both sweep area and angular momentum are always conserved. Not only does the Calculus describe planetary motion, but that a stable solar system must have planets follow the Second Fundamental Theorem in operation.

¹$(1/2){\displaystyle \int r^{2}d\theta =(1/2){(ed)}^2}{\displaystyle \int [1/{(1+e\sin \theta )}^2]}d\theta$

after substituting a = 1, b = e in two integral formula taken from Lide et al.⁴:

$=\left(1/2\right){\left(ed\right)}^2\{ecos\theta /[\left(1^2–e^2\right)(1+esin\theta )\left]+\right[1/\left(a^2–e^2\right)\left]\left[2/{\left(1^2–e^2\right)}^{1/2}\right]\right[ta{n}^{–1}[(tan\theta /2+e)/{\left(1^2–e^2\right)}^{1/2}]\}$

Planets are arranged in orbits of varying radii and energy. This may be roughly analogous to electronic orbital clouds in atoms, where electrons contain increasing orbital energy (and a less negative removal potential) at greater radii from the nucleus. For a given planet, at increasing values of r, potential energy likewise increases (becomes less negative) but at the same time its kinetic energy increases. The removal potential energy, the energy required to remove a planet from its orbit, is the integral of the gravitational force equation from radius r to infinity, or:${\displaystyle \underset{r}{\overset{\infty }{\int }}MGm/r^2=MGm/r}$ . At large values of r, the potential energy required to remove the planet to infinity is lower, as with electronic orbitals, since the energy released if it fell to the sun is larger. The analogy cannot be extended however since the wavelike nature of electrons dramatically affects behavior where the subatomic force field responsible is electrical. The responsible force field for the macroscopic planets is gravitational, where quantum mechanical effects of the wavelike nature of particles are not observable. Since all planets have varying masses, no consistent relation between removal potential energy or kinetic energy as a function of r was found (Table 1). However, the velocity of all planets, independent of their mass, directly decreases as the inverse square of the radius. This is because for a given gravitational flux region, large masses are attracted with large forces since more material is available to interact with the field. All objects fall in gravity at the same rate, independent of mass. This helps to explain energy, which indeed is not a vector quantity, would not itself explain the observed equal area sweep rates seen for the planets which have widely differing potential energies but nevertheless the same rate of fall due to gravity from the sun and planet.

The amazing finding is that for every planet the average potential energy U required to remove it from its orbit is precisely 2 times its average kinetic energy K. Since the total energy is T = U + K, this means that for all the planets the average potential energy U is –2K so that T = –2K + K = –K.

This arrangement can be theoretically described, where planets in any orbit of radius r must have sufficient velocity to oppose gravitational force, which also itself determines the potential energy for any particular mass. For example, the U:K ratio may be mathematically demonstrated from the original construct by Newton that equates centrifugal force mv²/r with centripetal force MGm/r², following the Third Fundamental Law of Physics. Multiplying both sides by r produces mv² = MGm/r. The expression on the right happens to be the integral of the from infinity to r and represents the magnitude of potential energy required to remove the planet. The expression on the left happens to be twice the kinetic energy of the mass m, where the kinetic energy obtained by a body that gains increasing velocity is the definite integral of the momentum with respect to change in velocity, or${\displaystyle \int mvdv=m{v}^2/2}$ . So the constant 2:1 U:K ratio observed here from actual astronomic data for all planets may apply for all orbiting bodies in the universe.

Although the Third Fundamental Law of Physics is typically applied for contact forces, where equal and opposite forces are exerted on bodies in contact, Newton extended this Law to apply to orbiting planets that are not in direct physical contact with the sun. This is because planets are attracted by an invisible force due to gravitational fields from the sun and the planet that each act from a distance, while at the same time are characterized with a centrifugal force due to tangential velocity around a central point, equal and opposite to the attractive invisible force preventing escape. We do not know whether planets were thrown from the sun, thus changing speed until gravitational energy equilibrated, or rather were fast–traveling before being captured and turned by the solar and planet gravitational fields. So we do not know whether one force is an actual applied force, and the other a reactive force, or vice versa, but the Third Law applies much like a tug of war, but between two objects connected with invisible gravitational fields from each.

Since kinetic and potential energies interconvert as a planet orbits from perihelion to aphelion with differing velocities, one possibility is that this compares to an oscillating weight on a spring. However, velocity is a minimum when a spring is stretched where accelerative force is maximum, while planet velocities are greatest when the gravitational acceleration is also greatest. Nevertheless, the total energy remains conserved for both systems, where the potential and kinetic energy interconvert accordingly throughout a cycle. For planets, both the total energy and the 2:1 potential: kinetic energy ratio remains conserved throughout an orbit. For Pluto at perihelion, the kinetic energy is 2.71 x 10²⁹ J but at aphelion is 1.00 x 10²⁹ J (Table 1). The removal potential energies at perihelion/aphelion are 2.63 x 10²⁹ and 4.36 x 10²⁹ J. For both positions, again the potential energy required to remove a planet from its orbit is approximately twice the kinetic energy of motion (Figure 2).

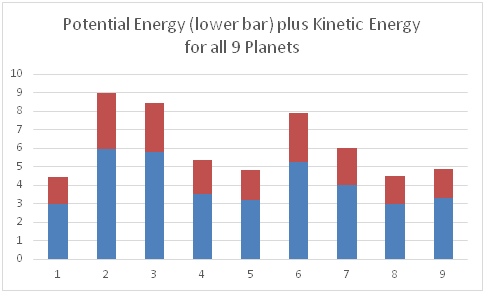
Figure 2 Chart showing the relative contributions of potential energy GMm/r (bottom portion of each bar) and kinetic energy mv²/2 (upper portion) to the total energy for the planets, in order: Mercury (J x 10³²), Venus (J x10³³), Earth (J x 10³³), Mars (J x 10³⁸), Jupiter ((J x 10³⁵), Saturn (J x 10³⁴), Uranus ((J x 10³¹), Neptune (J x 10³³), and Pluto (J x 10²⁹). Potential energy is 1/3 of the total energy, and kinetic energy is thus consistently 2/3 of the total energy for each planet.

An amount defined as the total energy T, which is the negative potential to remove the planet from its orbit plus the kinetic energy, are constant (within observational error) between the two extremes (perihelion 1.65, aphelion 1.63 x 10²⁹J). Note that the multiple of rv is approximately the same within measurement error (2.71 x 10¹⁶ m²/s at perihelion, 2.73 x 10¹⁶ at aphelion).

This adds to our understanding of the nature of gravity. Similar to electric and magnetic fields, the mechanism by which gravitational fields always emanate from an object with mass is completely unknown. Recent claims that gravity travels as a wave at light speed has been refuted.⁵ The recent detection of what are argued to be waves of gravity has not been shown to be characterized with a wavelength or frequency. And extremely miniscule positional shifts of detectors on earth cannot known with certainty to be caused solely by a gravity impulse that traveled as a wave from a distant mass to earth, rather than possibly an increased gravity amplitude due to a lateral shifting field that already existed in the vicinity of the detector, or other causes. Gravity cannot be refracted or reflected as for example light waves can. It must be emphasized that gravity is not energy, but is a field in which a force can be generated by a contained mass. Neither mass loss nor energy loss is required from an object with mass to be permanently surrounded by gravity. Energy dissipation is not required for gravity to exist around any particular mass. Light on the other hand is a wave and is energy given by E = hf where h is Planck’s constant and f is the frequency of the light. The speed of light is given by$c=f\lambda$ where$\lambda$ is the wavelength of the light, but no such equation is known or suggested for any putative wave of gravity. The fact that loss of mass creates energy is true, but since gravity is not energy, mass loss does not necessarily create gravity as has been claimed.⁶ Instead, gravity around any mass would cease to exist if that mass were annihilated. If energy were converted into mass, then gravity would surround that mass. However, the information taken together here, suggests that the notion that gravity might be produced to travel continuously from that mass into space, in a manner comparable to light photons produced continuously from a star, is not considered likely. Further, the notion that gravity waves exist like cosmic rays or infrared radiation from subatomic or atomic vibrations is also not likely. For example, it is possible to determine whether the intrinsic gravitation strength of matter is altered by temperature and molecular or atomic/subatomic motion. Solving, G = rv²/M where v is the velocity of the planet at its radius r, and M is the mass of the sun. For Pluto, where temperatures are extremely low, averaging –228°C,⁷ the value for G from observed data is G = 6.77 x 10^–11 m³/kg–sec². This differs from the accepted value for G by only 1.4%. On the other extreme, for Mercury where temperatures can be extremely high, averaging 167°C, the value from observed Mercury data is G = 6.54 x10–11 m³/kg–sec². This differs from the accepted value by only 1.9%. This suggests that changes in molecular motion may not be particularly significant in altering gravity or causing it to exist, considering the temperature change is nearly 400 K. As Newton originally wrote, the mechanism responsible for the existence of gravity around any mass remains a complete mystery to us.

The perihelion position in space that earth occupies is actually farther from the sun at all orbit times than when the planet arrives at aphelion (Figure 3). Traveling through perihelion, the planet approaches the barycenter and so does the sun, until their minimum radius is achieved, with a higher gravity flux than the instant before. But this is the farthest the sun is from the perihelion position because the sun must rotate around the common barycenter, which is a recession away from the earth’s perihelion position. Leaving perihelion, the planet radii increase as the sun also shifts around the barycenter toward the perihelion position in space. This causes a higher flux at the perihelion position (and a lesser flux on the earth) than when the sun was further from the perihelion position that the earth vacated. In other words, when the sun is closest to the planet (when the planet occupies perihelion), the sun is actually further from this perihelion position at that time. So the coordinate in space at which perihelion exists contains the minimum gravitational flux from the sun (that the coordinate will ever have) just as the planet arrives there. This extends to any point in the orbit of any planet. The sun is always furthest from a particular orbital position at the time the planet arrives at that position.

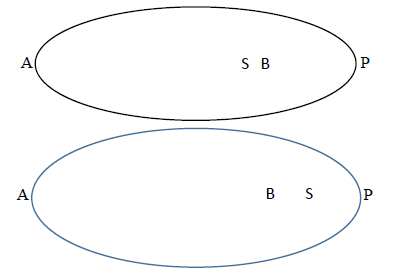
Figure 3 An exaggerated elliptic orbit of a sample lone planet, where aphelion A, perihelion P, barycenter B, and the sun S positions are labeled. When the planet occupies the perihelion position in space at P (top diagram), the sun S is closest to the planet but furthest from the P position in space, on the opposite side of barycenter B. When the planet occupies the aphelion position A (lower diagram), the sun is furthest from the planet but closest to the perihelion P position in space on the same side of the barycenter. Although the entire system may rotate and drift in space due to galaxy rotation and translation, the relative positions of A, B, and P are fixed with respect to each other. The center of mass at B does not exhibit a relative shift, while angular momentum is conserved, as the sun and planet orbit around it. Thus planets follow gravitational flux minima throughout an orbit, while continuously falling, as radial distances to the sun increase (from P to A) and decrease (from A to P) in cycles.

The old notion that the sun revolves around the earth was replaced, after detailed telescopic observations by Galileo, with the idea that the earth revolves around the sun. Both claims are partially correct and partially incorrect at the same time. We now know from Kepler’s observations that spatial objects orbit together around a common center, where for example the moon orbits the earth as the earth orbits the moon around the common center of mass barycenter. The earth and sun also both exhibit lateral velocity around a common point, the focus of the solar ecliptic. The largest motional effect on the sun is caused by Jupiter, the most massive of the planets at 1.9 x 10²⁷ kg with a closest approach of 7.4 x 10⁸ km. This means that the center of mass between Jupiter and the sun, the focus of the ecliptic plane about which the sun orbits, is approximately at the edge of the sun. The center of mass is obtained from$m_j{r}_j=M{r}_s$ . Rearranging, and since$r_e+r_s=R$ , the sun–Jupiter distance at any orbital position, then$r_j=RM\left(m_j+M\right)$ which at perihelion is 7.4 x 10⁸km (1.9 x 10²⁷kg)/(1.99 x 1030 + 1.9 x 10²⁷kg) = 7.1 x 10⁵ km, similar to the radius of the sun. The lateral velocity of the sun could be estimated knowing that$v=rw$ and that the angular velocity$w$ is constant for both the sun and Jupiter that rotate in synchrony, $v_s=r_{s}w$ and $v_j=r_{j}w$  where$v_s$ and$v_j$ are sun and Jupiter lateral tangential velocities and$r_s$ and$r_j$ are the distances from the sun and Jupiter to the common center of mass about which each rotate, so $v_s=r_s\left(v_j/r_j\right)=r_s[v_j/\left(R-r_s\right)$ . Using the average velocity of Jupiter at$v_j=47.4km/s$ , the lateral velocity of the sun would be about$v_s=46m/s$ . Because many planets all co–orbit the sun and each arrive at perihelion positions at various times, the sun actually traces out a spiral–like pattern around the focus of the solar ecliptic.⁵

Stars orbiting about a barycenter in a galaxy must also do this, and galaxies themselves rotating among each other also. In this way, the universe of matter can be in a regular equilibrium steady–state, rotating and perpetually “falling”, with conservation of sweep area, energy, and angular momentum throughout any cycle with the potential energy from a barycenter of mass that is twice its kinetic energy of motion around that point. There are an estimated 1 mole² or 600 billion trillion, light–emitting stars in the two trillion galaxies of 300 billion stars each in the known universe of matter, with innumerable planets all following these gravitational principles. The universe of space is infinite without limit, so the widely held notion that the “universe is expanding” requires clarification. The entire universe of matter is not expanding either, since planet distances from the sun for example are not expanding (other than slight increase due to loss of sun mass from fusion reactions). The idea that it is galaxies that recede from each other is complicated by the fact that galaxies undergo rotation around a common center so that some stars approach observers on earth while other stars are receding. Previous discussions have been presented on the possibility from entropy considerations that the galaxies of the universe may exist in a steady–state dynamic equilibrium condition.

Knowing that gravity intensity from any mass follows the inverse square law from the center of that mass, independent of any rotational motion of the mass, it is difficult to explain why all planets lie essentially on a flat planar ecliptic, rather than in randomly oriented orbits of differing radii. Although the dispute is endless, one common notion is that planets exploded from the ecliptic perpendicular to the spinning axis of the sun. This however is not consistent with the facts that 1) the sun axis actually is tilted from the ecliptic, and 2) Halley’s comet, which orbits the sun, follows a completely different plane. Similarly, the moon, also argued by some to have escaped from the earth, orbits${20}^o$ tilted from the earth spin axis. And objects thrown from a rotating body should spin in a direction opposite that of the body, and yet six planets rotate counterclockwise as does the sun. Venus spins clockwise and Uranus spins sideways. Also, several planets consist of gasses while the others are rock, all with differing chemical compositions.

Further drama is that the moon is annular, with a perfect diameter to block the sun’s rays during a full eclipse viewed from earth except for an outer ring of light. Also, no relationship is found between planet orbit radius, or kinetic energy, with the energy that would be released if the planet were to fall back into the sun (calculated as the fall potential in Table 1), whereas the 2:1 ratio of the removal potential energy, the energy required to remove a planet from its orbit out to infinity, with the kinetic energy of the planet holds for the entire solar system. So the planets appear to have been captured by the sun, rather than exploding from it.

Taken together, these phenomena are unlikely to be the result of a random explosion, and support the writings of Sir Isaac Newton that the solar system appears to function like a vast wound clock, not the result of an accidental random process. Extending this analogy, one may consider the revolution times for planets as comparing with the revolution times of the hands on a clock, except that the largest radius hand, Pluto, is the slowest hand with the largest period,$2\pi$ radians per 250 earth years, and the fastest hand, Mercury at$8\pi$ radians per earth year is at the shortest radius and smallest period. For planets, real data from NASA were used to plot orbit periods as a function of mean distances from the sun. The curve follows an exponential equation $t=4.4r^{1.5}$ and with t in quarter years and r is in hundreds of million miles (Figure 4). If the hands on a clock were masses held from the center by a gravitational inverse square law source, and the lengths of the hands were arranged properly so that the hour hand were the longest and slowest hand at$2\pi$ radians per day, then a similar exponential equation is followed (data not shown), The speed of the second hand is$2\pi$ radians per minute, and the minute hand$2\pi$ radians per hour. Planets do appear to behave like hands on a vast clock. Each orbit of the outermost planet Pluto corresponds to 1,000 Mercury orbit times and each Earth millennium is recorded in 4 Pluto orbits. In the 6,000 years of known human history since 4,000 B.C., Pluto has orbited 24 times.

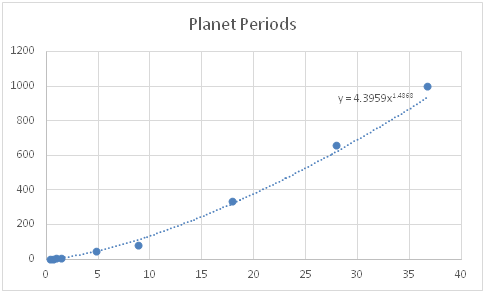
Figure 4 Revolution time of planets: The time to complete one orbit in Mars orbit units (= 3 months) is plotted for each planet on the vertical axis, as a function of distance from the sun (miles x 10⁸). Pluto requires 1,000 Mars obit units and Earth requires 4.

The precise circumferences for the orbits of all planets were computed with an elliptic integral and plotted as a function of mean distance from the sun (Figure 5). The circumferences of Saturn, Uranus, and Neptune are precisely 10, 20, and 30 Earth orbit circumferences respectively. Jupiter and Pluto are 12 and approximately 100 circumferences of Mercury. Continuing the analogy of planet orbits with electron orbitals around nuclei, planets also exhibit wavelike character while continuously wobbling from minimum to maximum radius in continuous cycles or waves, while conserving total energy in that particular orbital. So the solar system seems comparable in these ways with a giant atom, with the sun as its nucleus and planets as the wave–generating objects in orbit around it. The arrangement of quantized energy levels as in atoms may be necessary for stable resonance of each orbital without perturbing neighboring planetary orbits.

Figure 5 The precise orbit circumferences for each planet were computed with the Calculus integral and plotted as a function of average distance from the sun. Jupiter is 12 orbits of Mercury and Pluto is 100 orbits of Mercury. Saturn, Uranus, and Neptune are 10, 20, and 30 earth orbits, respectively. Uranus is 2 Saturn orbits and Neptune is 3 Saturn orbits.

The circumference integral employed is the elliptic integral where$C=4a{\displaystyle \underset{0}{\overset{1.57}{\int }}{\left[\left(1-e^2\right)si{n}^{2}x\right]}^{0.5}d}x$ . Here$e$ is the eccentricity given by$e=\left(a-b\right)/\left(a+b\right)$ where$a$ is the major axis radius at aphelion and$b$ is the minor axis radius at perihelion.

Thanks go to Palomar College students for suggesting this paper be written and for insight. Isaac Newton is again acknowledged for writing that the solar system is designed like a finely–tuned wound–up clock.

Author declares there is no conflict of interest.

1. Giancoli D. Physics for Scientists and Engineers. USA: Prentice Hall; 2009.
2. Williams DR. Planet Fact Sheet. USA: NASA Goddard Space Flight Center; 2106.
3. Larson R, Edwards BH. Calculus. 9th ed. USA: Brooks/Cole Publishing; 2010.
4. Lide DR. CRC Handbook of Chemistry and Physics. 88th ed. USA: CRC Press; 2004.
5. Sauerheber RD. Gravity Contrasted from Light and Other Fields, Energetics and Solar System Dynamics. Fundamental Journal of Mathematical Physics. 2016:1–11.
6. LIGO. Gravitational waves detected 100 years after Einstein’s prediction. USA: LIGO Hanford Press Release; 2016.
7. NASA. Solar System Exploration. USA: NASA; 2012.
8. Jones BW. Exoplanets: search methods, discoveries, and prospects for astrobiology. International Journal of Astrobiology. 2008;7:279-292.
9. Sauerheber R, Espinoza E. Characteristics of Light: Velocity, Massless Energy, and Special Relativity. Optik, International Journal for Light and Electron Optics. 2018;168:974-986.
10. Sauerheber R. Thermodynamics and Entropy in Natural and Artificial Systems. American Research Journal of Chemistry. 2018;2(1):1-26.