This study is based on latitude measurements at the helio-meridian of two trans-equatorial coronal holes. After applying a simple algorithm based on super-radial expansion to the observation times, and translating these times to Earth’s bowshock, the measurements are compared with those of solar wind speed observed by the Wind and ACE spacecraft at those times. These comparisons reveal a causal relationship between the latitude range of the coronal hole open flux and the solar wind speed at the bowshock. Regression formulae are provided for predicting the speed of the fast solar wind from the latitude range of the coronal hole boundary within $\pm {20}^{\circ }$ of the helioequator.

The existence of coronal holes as regions of open magnetic flux on the Sun was predicted in the 1960s,¹ and they were first observed in spectro-heliograms from rocket experiments.^2,3 Subsequently seen from space observations as striking dark features in X-ray and EUV (extreme ultraviolet) images of the Sun, they were confirmed by Krieger et al.⁴ to be sources of the recurrent high-speed solar wind streams. The Skylab CH1 coronal hole^5,6 was the first trans-equatorial structure to be observed.

It is now well known that the fast solar wind emerges primarily from coronal holes and expands to fill the majority of the heliospheric volume with speeds from 450 to 900 km/s,^7-9 whereas the slow component (250 to 450 km/s) is associated with coronal streamers^10,11 and may also have contributions arising from boundary flow along current sheets, the magnetic reconnection of closed-field loops, and the boundaries of coronal holes.¹² The passage of low-latitude coronal holes across the helio-meridian often results in weak to moderate magnetic storms within geospace,^13,14 the intensity being mainly dependent on the orientation of the IMF and the dynamic pressure of the solar wind. (For the purposes of this study, the helio-meridian is defined as the central, fixed (non-rotating) solar meridian on the Sun-Earth line.)

The two trans-equatorial coronal holes used in this study crossed the helio-meridian during August 26 to 28 1996 and June 28 to July 1 2005 (Figure 1). The images were recorded at the L1 Lagrangian point using the Extreme Ultraviolet Imaging Telescope (EIT) aboard the Solar and Heliospheric Observatory (SOHO) spacecraft.¹⁵ SOHO Coronal Diagnostic Spectrometer (CDS) measurements of the 1996 coronal hole by Bromage et al.¹⁶ show that such features appear most distinctly in Si XII at 2x10⁶ K, which is comparable with the EIT Fe XII $195\text{Å}$ image at 1.6x10⁶ K. Consequently, coronal holes are usually measured using images at this wavelength. (The variation of temperature with height is considered in the Discussion.)

The coronal hole boundaries were defined using a histogram-based threshold segmentation technique,^17-20 which searches for a dominant local minimum in the intensity distribution of the EUV image. (With this technique, the boundaries (shown in red in Figure 1) can be measured to an uncertainty not exceeding $\pm 1^{\circ }$ .) Using the IDL (Interactive Data Language) package ImageTool, the 2D SOHO EIT 195$\text{Å}$ images were then transformed into 3D and overlayed on a spherical grid, and each grid was rotated through the helio-meridian in 2-hour increments. At each increment the latitude coverage was measured (Figure 2).

Figure 1 Images of the Sun at 195 $\text{Å}$  from the EIT instrument aboard the SOHO spacecraft at L1: (left) August 26 1996 at 19:16 UTC; (right) June 29, 2005 at 21:48 UTC. (Courtesy of J.B. Gurman, NASA GSFC.) The boundaries (shown in red) were determined using threshold segmentation.

Figure 2 Variation of the latitude coverage of the two coronal holes: (a) August 26 to 28 1996; (b) June 29 to July 1 2005 (day 31 is July 1). (The uncertainty in the latitude coverage measurements is estimated not to exceed $\pm {\text{1}}^{\circ }$ )

From these measurements the latitude range between five selected latitude limits $(\pm {\left[10,20,30,40,50\right]}^{\circ })$ was determined (Figure 3). Within these five limits (four in the case of the 1996 event) the latitude range clearly increases to a peak value and then decreases (this tendency being more pronounced with increasing latitude). (A note on helio-latitude terminology: range defines the extent of the open flux between the specified limits, whereas coverage (from which the range is derived) quantifies the north-south extremities of the open flux.)

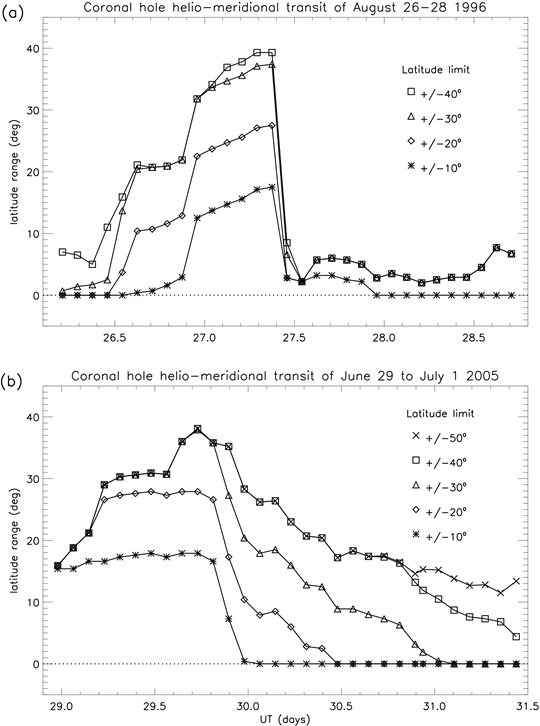
Figure 3 Variation of the latitude range of the two coronal holes, within the indicated latitude limits: (a) August 26 to 28 1996; (b) June 29 to July 1 2005 (day 31 is July 1). (Based on the latitude coverage, the uncertainty in the latitude range does not exceed $\pm {\text{2}}^{\circ }$ )

The particle flux emanating from these coronal holes resulted in an increase in the solar wind speed at Earth’s bowshock (Figure 4), this association having been confirmed for both events in the Reports on Solar and Geophysical Activity from NOAA (https://www.swpc.noaa.gov). Measurements of the solar wind and the IMF made by the Wind and ACE spacecraft in the vicinity of L1 are readily available from the Goddard Space Flight Centre (http://omniweb.gsfc.nasa.gov/), and it is these data (specifically, solar wind bulk speed translated to Earth’s bowshock) that have been used in this study.

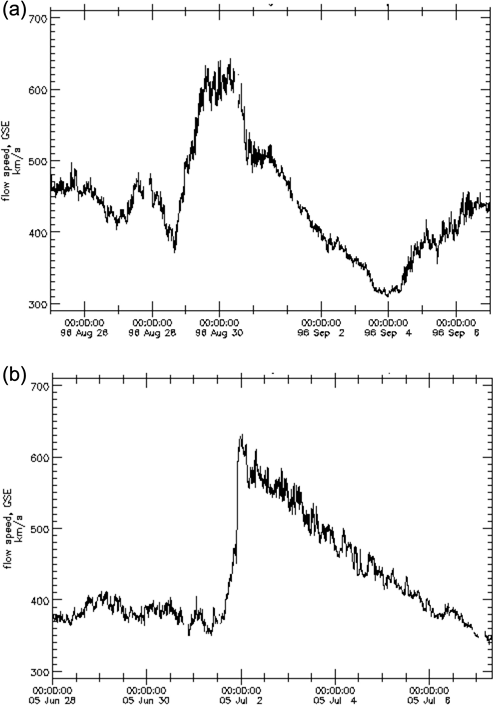
Figure 4 Solar wind bulk speed measured at L1 and translated to Earth’s bowshock: (a) August 28 to September 6 1996; (b) June 28 to July 6 2005. (From combined Wind and ACE data, courtesy of J.H. King and N. Papatashvilli, NASA GSFC, CDAWeb.)

In each case the general form of the time series for the solar wind speed is not dissimilar to that for the latitude range of the coronal holes themselves (though of about twice the duration). A fast solar wind stream undergoes super-radial expansion within about 2.25 solar radii of Sun-centre,^16,21,22 which might explain the longer duration of the solar wind speed time series. This conjecture will now be investigated.

Figure 5 shows the geometry of the super-radial expansion of the fast solar wind stream resulting from the coronal hole of August 26-28 1996. Analysis by Bromage et al.¹⁶ of observations with the SOHO Ultraviolet Coronograph Spectrometer (UVCS) reveals that the boundary of the hole subtended an angle at Sun-centre about ${10}^{\circ }$ wide at$1.0R_s,$  ${40}^{\circ }$ wide at 1.75 $R_s$ and ${60}^{\circ }$ wide at 2.25 $R_s$ , with radial propagation beyond that distance (see Discussion for further details). Dobrzycka et al.²³ found that the maximum super-radial expansion of a coronal hole boundary typically occurs at 1.5 $R_s$ , followed by an exponential reduction in the width of the boundary (with scale factor 0.5 $R_s$ ). Combining the results of these two studies, the red lines in Figure 5 estimate the boundary of the open field as it expanded into the corona, and indicate that, beyond 2.25 $R_s$ , the boundary subtended an angle of $\pm {30}^{\circ }$ from the Sun-Earth line in the ecliptic plane.

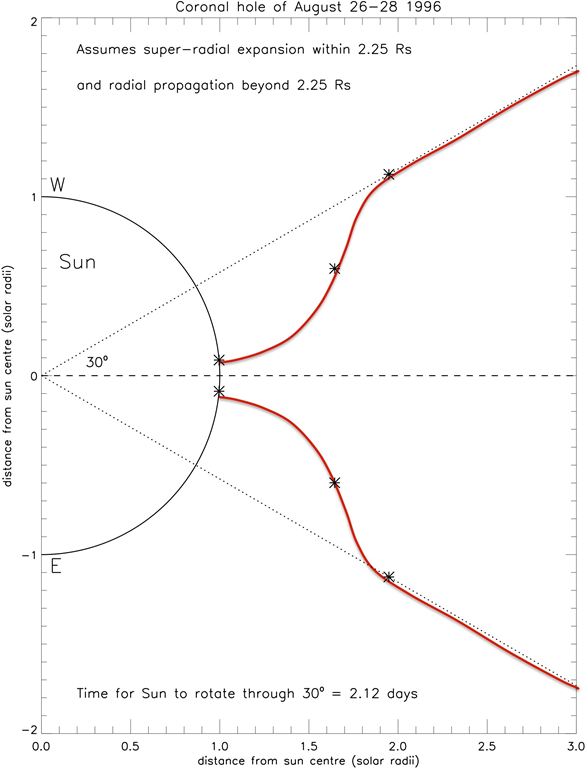
Figure 5 Super-radial expansion of the fast solar wind stream resulting from the coronal hole of August 26-28 1996.^16,23

With a Carrington sidereal solar rotation time of 25.38 days,${30}^{\circ }$ is equivalent to a duration of 2.12 days. In other words, the leading edge of the fast stream from the coronal hole will be directed at Earth 2.12 days ahead of the time when the corresponding leading edge of the coronal hole crosses the helio-meridian. Similarly, the trailing edge of the fast stream will be directed at Earth 2.12 days after the trailing edge of the coronal hole crosses the helio-meridian.

The four UTC time series used in this analysis $(t,t_s,t_{sb},t_b)$ are shown schematically in Figure 6 (using the 1996 event as an example), and are related as follows - 

Figure 6 Schematic showing the effect of applying super-radial expansion and translation on the time series for the coronal hole transit of August 26 to 28 1996 (days 32 to 34 are September 1 to 3): (a) symmetrical scaling; (b) offset scaling. (The blue lines show the effect on the time of the peak in the latitude range. The red lines are not scaled.$t$ = observation times at the Sun,$t_s$ = $t$ after scaling,$t_{bs}$ = $t_s$  translated to bowshock,$t_b$ = $t$ translated to bowshock).

1. $t$ : measurements of the latitude coverage at the helio-meridian;
2. $t_s$ : values of $t$ scaled according to super-radial expansion in the corona;
3. $\Delta t$ : translation time from the corona to the bowshock;
4. $t_{sb}$ : values of $t_s$ translated to the bow-shock by $\Delta t$ ;
5. $t_b$ : values of $t$ translated to the bowshock by $\Delta t$ , without scaling.

 The latitude range and the solar wind speed will be compared at times $t_{sb}$ (the solar wind speed being derived by interpolation from data files at 1-hour resolution). The solar wind speed at times $t_b$ (without scaling, shown in red in Figure 6) will also be used to compare with the results from super-radial expansion.

To account for super-radial expansion, time series $t$ in Figure 3 was scaled according to an algorithm based on the ${30}^{\circ }$ (2.12 day) angle in Figure 5. Two scaling methods were used: (1) symmetrical, and (2) asymmetrical (subsequently named offset, for clarity).

Symmetrical scaling

Let the time series $(t)$ of latitude coverage at the Sun be $t_0\mathrm{.....}{t}_n$ (t measured in decimal days), and the scaled time series ($t_s$ ) be $t_{s0}\mathrm{.....}{t}_{sn}$ . Applying the super-radial 2.12 day lead and lag times, the duration ($d$ ) of $t_s$ is then given by:

$d=\left(t_n+2.12\right)-\left(t_0-2.12\right)=t_n-t_0+4.24$   (1)

 and each element $t_{si}$ in the scaled time series ($t_s$ ) is given by:

$t_{si}=t_0-2.12+d\left(i/n\right)$   (2)

 The time series $t$ and $t_s$ are shown schematically in Figure 6a, in which the 2.12 day lead and lag times between $t$ and $t_s$ are clearly evident. The blue lines show the effect on the time of the peak in the latitude range, and it is clear that there is a discrepancy between the times with and without scaling.

Offset scaling

Symmetrical scaling is centred at the mid-point ( $t_{n/2}$ ) of time series $t$ , not necessarily at the time of peak latitude range ($t_p$ ). However, in cases when the variation in latitude range is not symmetrical ( $t_{n/2}\ne t_p$ , such as in these events), an alternative approach is to apply offset scaling. This is similar to symmetrical scaling, except that the rising and falling phases are treated separately. We assume that the centre of the peak in the latitude range occurs between elements $n1$ and $n2$ in time series $t$ . (A slight adjustment will be required if the peak occurs at a specific element, but the principle remains the same). Let $t_0\mathrm{.....}{t}_{n1}$ and $t_{n2}\mathrm{.....}{t}_n$ represent the rising and falling phases in the observed time series. Applying the super-radial 2.12 day lead and lag times, the rising and falling durations ($d_1,d_2$ ) are then given by:

$d_1=t_{n1}-\left(t_0-2.12\right)=t_{n1}-t_0+2.12$   (3)

$d_2=\left(t_n+2.12\right)-t_{n2}=t_n-t_{n2}+2.12$   (4)

 Each element ($t_{s1i},t_{s2i}$ ) in the rising and falling phases ($t_{s1},t_{s2}$ ) of the scaled time series ($t_s$ ) are then given by:

$t_{s1i}=t_0-2.12+d_{1}i/n_1$   (5)

$t_{s2i}=t_{n2}+d_{2}i/n_2$   (6)

 The scaled time series for the rising and falling phases are then combined to give $t_s$ :

$t_s=\left[t_{s1},t_{s2}\right]$   (7)

 The effect of offset scaling on the observation times at the Sun is shown schematically in Figure 6b.

Translation to the bowshock

The delay time ($\Delta t$ ) between the peak in latitude range ($tp$ ) and the peak in each of the speed profiles ($t_{vmax}$ ) can be readily determined:

$\Delta t=t_{vmax}-t_p$   (8)

For example, in Figure 3a the peak UTC ($t_p$ ) was estimated to occur at 27.1667 days (the mid-point between elements 9 and 16), whereas in Figure 3b (which has a clearly defined peak) element 10 was selected (29.7292 days). The UTCs of the peaks in solar wind speed were determined from the data files corresponding to Figure 4. In the case of the 2005 event $t_{vmax}$ is clearly defined and happens to be at 00:00 UTC on July 2. However, for the 1996 event $t_{vmax}$ is less obvious, so 550 km/s was chosen as the defining limit, and the mid-point (00:40 UTC on August 30) between the times of increasing and decreasing transition through this limit (08:08 UTC on August 29 and 17:13 UTC on August 30, respectively) was selected. The values of $\Delta t$ for the 1996 and 2005 events, expressed in the form dd:hh:mm, are therefore 02:21:40 and 02:05:30 (respectively). Time series $t_s$ , from both the symmetrical and offset scaling, are then translated to Earth’s bowshock by adding the delay time $\Delta t$ . If $t_{sb}$ represents the scaled time series ($t_s$ ) translated to the bowshock, then -

$t_{sb}=t_s+\Delta t.$   (9)

 The original non-scaled time series $t$ was also translated to the bowshock (shown by the red lines in Figure 6) -

$t_b=t+\Delta t.$   (10)

 By this means, the efficacy of translation alone can be compared with that of scaling and translation.

Effect of scaling and translation

Figure 7 compares the solar wind speed (dashed) and the latitude ranges with offset scaling applied, both plotted at times $t_{sb}$ , and in both events there appears to be a similarity between the time series of speed and latitude range, and hence the possibility of a significant correlation. For comparison, the red curve shows the original latitude range at $\pm {40}^{\circ }$ , plotted at times $t_b$ (i.e. without scaling applied). Similarly, Figure 8 shows the same comparison using symmetrical scaling, but in this case the peaks in the solar wind speed and the latitude ranges do not coincide. Consequently, in the case of symmetrical scaling, the correlation between speed and latitude range is expected to be less significant.

Figure 7 Solar wind speed (dashed) and latitude range (with offset scaling) at the bowshock (both plotted against $t_{sb}$ ): (a) August 26 to September 2 1996 (days 32 and 33 are September 1 and 2); (b) June 29 to July 5 2005 (days 31 to 35 are July 1 to 5). (The non-scaled latitude range for the $\pm {40}^{\circ }$ limit (plotted against $t_b$ , in red) is shown for comparison.)

Figure 8 Solar wind speed (dashed) and latitude range (with symmetrical scaling) at the bowshock (both plotted against $t_{sb}$ ): (a) August 26 to September 2 1996 (days 32 and 33 are September 1 and 2); (b) June 29 to July 5 2005 (days 31 to 35 are July 1 to 5). (The non-scaled latitude range for the $\pm {40}^{\circ }$ limit (plotted against $t_b$ , in red) is shown for comparison.)

The blue lines in Figure 6 show the effect of scaling and translation on the time of peak latitude range, and it can be seen that in the offset case the peaks are coincident, whereas in the symmetrical case they are not. In both events, because $t_{n/2}\ne t_p$ , symmetrical scaling skews $t_s$ such that, after translation $t_{vmax}$ ,no longer coincides with $t_p$ . The further is the peak from the mid-point, the greater is the discrepancy, and offset scaling compensates for this effect. Paradoxically, applying an offset might be thought to assume a result that is not yet proven: this issue is considered in the Discussion.

Having confirmed in Figures 7 and 8 that the time series of the solar wind speed and the latitude range have similar profiles, suggesting a possible correlation (particularly in the case of offset scaling), this conjecture will now be tested by combining the elements for both events. The fast component of the solar wind emanates from coronal holes at speeds $\gtrsim$ 450 km/s, and the transition from slow to fast occurs at $\approx$ (400 to 450) km/s, so a correlation test using speed thresholds might be revealing. In this test, the correlation of solar wind speed against latitude range is determined, in each of the 5 latitude bands, for speed thresholds from $>$ 350 to $>$ 540 km/s, in 5 km/s increments. (During the two events, at times $t_{sb}$ , the maximum solar wind speed was 626 km/s, but the sample sizes at speed thresholds beyond $>$ 540 km/s were found to be too small to provide a consistent correlation coefficient.) The disadvantage of using inclusive latitude limits ($\pm$ 10, 20, 30 and ${40}^{\circ }$ ) is that the speed associated with plasma from higher latitudes may be biased by that from lower ones (which is likely to be dominant). Consequently, differential latitude bands were used $(\pm {(0-10)}^{\circ },\pm {(10-20)}^{\circ },\pm {(20-30)}^{\circ },\pm {(30-40)}^{\circ }$ and $\pm {(40-50)}^{\circ }).$ These bands were derived by subtracting adjacent limits, for example $\pm {(20-30)}^{\circ }=\pm {30}^{\circ }-\pm {20}^{\circ }$ . (Of course, thelimit is not affected; only the higher latitude limits require conversion to differential bands.)

The results of the correlation tests are shown in Figure 9, including those without scaling applied for comparison with the effects of offset and symmetrical scaling. (It is emphasised that these are speed thresholds, so each value represents all speeds above that value.) The two dashed lines at $>$ 400 and $>$ 450 km/s mark the speeds which define the limits of the transition between the slow and fast solar wind, and the dotted lines mark the correlation coefficients above which the relation is considered to be significant $(\rho =0.6)$ and very significant $(\rho =0.8)$ . Because zero latitude ranges are valid samples, at any given speed threshold the sample counts for each of the five latitude bands are equal (and are the same as those for the latitude limits). Figure 9 reveals the following -

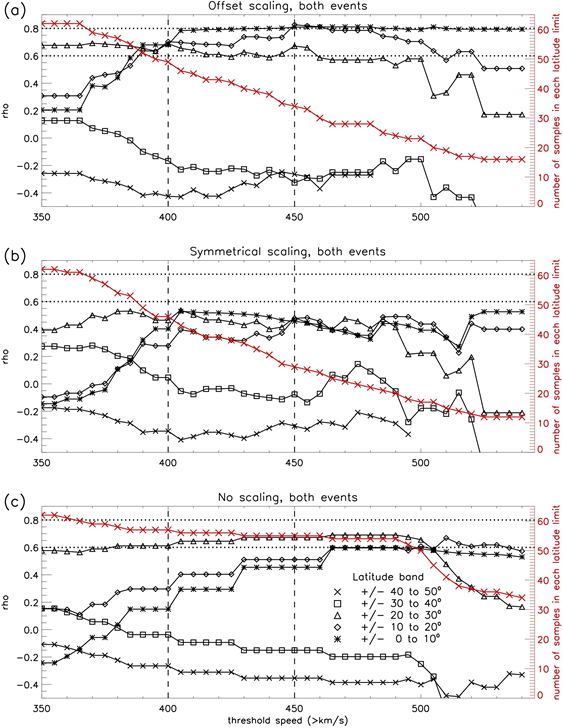
Figure 9 Variation of correlation coefficient (between latitude range and solar wind speed) with threshold speed, for differential latitude bands, for both events combined: (a) offset scaling; (b) symmetrical scaling; (c) without scaling.

• General comment: in all three cases (a, b and c), the higher latitude bands $(\pm {\left(30-40\right)}^{\circ } and\pm {\left(40-50\right)}^{\circ })$ all give very poor correlations $(\rho <0.3)$ , implying that the flux at these latitudes is not geo-effective.

1. Offset scaling. At speeds $>$ 400 km/s there is a distinct change in behaviour at lower latitudes $(\pm {\left(0-10\right)}^{\circ },\pm {\left(10-20\right)}^{\circ }and\pm {\left(20-30\right)}^{\circ })$ . Significant correlations are revealed at these latitudes, intermittently at $\pm {\left(20-30\right)}^{\circ })$ , and consistently at $\pm {\left(0-10\right)}^{\circ }and\pm {\left(10-20\right)}^{\circ }$ (in particular, at $>$ 450 km/s, these correlations peak, and are very significant),
2. Symmetrical scaling provides poor correlations at all latitudes $(\rho <0.55)$ .

• Without scaling, only the $\pm {\left(20-30\right)}^{\circ }$ band gives significant correlations at speeds $>$ 400 km/s.

Table 1 lists the correlations coefficients from Figure 9, at $>$ 450 km/s, for each latitude band, and it is evident that only offset scaling at $\pm {\left(0-10\right)}^{\circ }$ and $\pm {\left(10-20\right)}^{\circ }$ gives correlations with $\rho >0.8$ . These results demonstrate that the fast solar wind is dominant within ${20}^{\circ }$ of the helio-equator, and beyond that limit there is a much weaker contribution.

The spread of the samples for these two very significant correlations ( $\rho$ = 0.81, 0.83) are shown in Figure 10ab, together with the regression equations, sample sizes, correlation coefficients and standard errors, These statistics are summarised in Table 2 (columns 2 and 3), which also includes the 1$\sigma$  uncertainties. Also included are the statistics for $\pm {\left(0-20\right)}^{\circ }$ (Table 2 (column 4) and Figure 10c), which reveal an even more significant correlation ($\rho$ = 0.87). The $\pm 2^{\circ }$ measurement uncertainty for the latitude range does not exceed the standard errors for the X-on-Y correlations.

Figure 10 Scatter plots of solar wind speed against latitude range for the fast solar wind ( $>$ 450 km/s), derived using offset scaling: (a)$\pm {\left(0-10\right)}^{\circ }$ ; (b) $\pm {\left(10-20\right)}^{\circ }$ ; (c) $\pm {\left(0-20\right)}^{\circ }$ . (The statistics are summarised in Table 2. The latitude range in (b) is limited to ${10}^{\circ }$ because, in the $\pm {\left(10-20\right)}^{\circ }$ band, there is no coincident open flux in both the N and S hemispheres (see Figure 2). V = solar wind speed (km/s), $L_R$ = latitude range (deg), SE = standard error.)

To conclude, if super-radial expansion is taken into account using offset scaling, within $\pm {20}^{\circ }$ of the helio-equator the latitude range of the coronal hole open flux at the helio-meridian gives a reliable prediction of the fast solar wind speed at the bow-shock. However, at $\pm {(20-30)}^{\circ }$ the reliability of the prediction is in question, and at higher latitudes it is invalid. Furthermore, when using either symmetrical scaling or none at all the method is invalid.

Super-radial expansion: background

The SOHO EIT 195$\text{Å}$  images (Figure 1) were formed from the Fe XII line, emitted by coronal plasma at a temperature of about 1.6x10⁶ K. The darkness of the coronal holes is due to the lower density of the plasma, as well as its somewhat reduced temperature (about 8x10⁵ K), which is free to expand into space along the open field. The boundary of the coronal holes is quite irregular, reflecting the structure of the adjacent closed-field loops. SOHO CDS images used by Bromage et al. (2000) show the emission at four different wavelengths, representing the solar plasma at four different temperatures and, hence, emission from four different heights in the solar atmosphere: He I (3x10⁴ K); Mg IX (1x10⁶ K); Mg X (1.3x10⁶ K); Si XII (2x10⁶ K, comparable with the EIT Fe XII 195 images $\text{Å}$ ). An estimate was thereby obtained of the expansion of the coronal hole boundary with height, from the upper chromosphere to the corona.

The field lines at the boundary were found to make an angle with the radial direction of $37\pm 3^{\circ },$ consistent with the angle commonly seen in EIT images at the polar coronal hole boundaries above the limb. SOHO UVCS data obtained by Bromage et al. on August 23, when the most southerly part of the coronal hole was on the eastern limb of the Sun, show that the hole was about ${40}^{\circ }$ wide at 1.75$R_s$ from Sun-centre, and about ${60}^{\circ }$ wide at 2.25 $R_s$ (see Super-radial expansion of the fast solar wind stream). This clearly suggests that the boundaries of the hole were diverging super-radially within this range. Thereafter the plasma was found to travel radially, the angle subtended by the boundary of the coronal hole being $\pm {30}^{\circ }$ from the Sun-Earth line in the ecliptic plane. Evidence for this behaviour is also reported by Dobrzycka et al.,²³ who found that the maximum super-radial expansion of a coronal hole boundary typically occurs at 1.5 $R_s$ , followed by an exponential reduction in the width of the boundary (scale factor 0.5 $R_s$ ), with subsequent radial expansion beyond 2.25$R_s$ . Dobrzycka et al. also report that polar coronal holes appear to have super-radial geometry with a divergence factor ranging from 6.0 to 7.5. Though the detailed structure in the boundary of both coronal holes varied on a time-scale of hours, the overall features rotated quasi-rigidly for several months, as was the case with the Skylab CH1 hole.⁶ This quasi-rigid rotation has also been seen in other (although not all) low-latitude holes.²⁴

Assumption of peak-to-peak association

This paper investigates potential relationships between the latitude range of coronal hole open flux at the helio-meridian and the solar wind speed at geospace. The critical factor in such a test is one of timing: how should the time series of the solar observations be converted to one that can be used to compare the appropriate speeds at geospace? To do so, it is necessary to associate a distinct feature in the latitude range profile at the photosphere with another in the speed profile at geospace (say, at the bowshock), and hence determine the travel time between these two locations. Both profiles first rise then fall, and so the peak value is the obvious choice for such a reference point. If coronal hole open field emanated radially from the photosphere (with respect to Sun-centre) then no scaling would be required and the conversion would simply be a matter of translation, based on the travel time between the two peak reference points at the Sun and the bowshock.

However, super-radial expansion is a phenomenon that is well-documented in the scientific record.^16,21-23 Consequently, before translation is applied, it must be taken into account by linearly expanding the time series of the latitude coverage at the helio-meridian to take account of the 2.12 day lead and lag times resulting from the ${30}^{\circ }$ super-radial angle, using either symmetrical or offset scaling.

Given that the latitude coverage of the open flux is asymmetric (which is the case for these events, and probably for most, taking into account the stochastic nature of the medium), then symmetric scaling will not suffice because the further is the peak from the mid-point, the greater will be the discrepancy (as shown by the blue lines in Figure 6b). Offset scaling compensates for this discrepancy by assuming a direct association between the time of the peak in latitude range and the time of the peak solar wind speed at the bowshock. However, this assumption might be thought to bias the outcome: are we assuming a result before it has been proven? The NOAA Reports on Solar and Geophysical Activity clearly associate the helio-meridional transits of these coronal holes with the corresponding increases in solar wind speed at the bowshock shown in Figure 4, but only in qualitative terms. This study makes the assumption that the association is quantitative i.e. that the two peaks can be related for purposes of scaling and translation. The results herein certainly support this assumption, and it remains to be seen whether or not future research will provide further justification.

Correlation tests and linear regressions

The computations in this study were carried out in IDL. The correlation tests in Figures 9 and 10 were performed using the CORRELATE function, which computes the linear Pearson correlation coefficient. In addition, the linear regression lines in Figure 10 were generated by the POLYFIT function, which uses a least-squares fit and also provides the standard error values and the $1\sigma$ uncertainties. (These functions assume random errors for the points being fitted and correlated.)

Variation of solar wind speed with longitude coverage

This study focusses on the variation of solar wind speed with coronal hole latitude coverage. A question arises: what about the variation with longitudinal coverage? The two coronal holes used in this study were more variable in latitude than in longitude. Furthermore, though they are most certainly ’low-latitude’, they can only be described as ’trans-equatorial’ during no more than 50% of their helio-meridional transit. Coverage measurements, be they latitudinal or longitudinal, can only be made at a fixed reference line (i.e. along the helio-meridian or helio-equator, respectively). Consequently, these two coronal holes are more suitable for the analysis of latitude coverage, not longitude. It remains for future studies to cover this aspect of the subject using coronal holes which are more suited to the task. However, because trans-equatorial coronal holes usually result from the migration of open flux from the polar holes, coronal holes with sufficient variation in longitude at the helio-equator will be much less common.

1. Two coronal holes were selected for analysis, one which crossed the helio-meridian from August 26 to 28 1996, the other from June 29 to July 1 2005.
2. Using SOHO-EIT 195$\text{Å}$ images of these coronal holes, measurements of the helio-latitude coverage of the open flux were taken at the helio-meridian within selected latitude limits.
3. When the super-radial expansion of the coronal particle flux and the translation to the bowshock are taken into account, the time series of the latitude ranges for both events resemble those of the solar wind speeds at the bowshock (measured by Wind and ACE).
4. Using offset scaling to account for the expansion, correlation tests demonstrate that, within $\pm {20}^{\circ }$ of the helio-equator, the latitude range of the coronal hole open flux ($L_R$ degrees) gives a reliable prediction $\rho >0.87$ ) of the fast solar wind speed ($V>$ 450 km/s) at the bowshock, according to the relation:

$V=5.27L_R+479.5$   (11)

5. Within $\pm {(20-30)}^{\circ }$ the reliability of the prediction is considerably less significant $(\rho =0.67)$ , and at $>{30}^{\circ }$ the correlation is negative.

The authors thank Dr. T. Laitinen (Jeremiah Horrocks Institute for Mathematics, Physics and Astronomy, University of Central Lancashire) for his advice regarding the super-radial expansion model. We also acknowledge NASA GSFC for the SOHO EIT images and the solar wind speed data.

None.

1. Wilcox JM. The Interplanetary Magnetic Field. Solar Origin and Terrestrial Effects. Space Sci Rev. 1968;8:258–328.
2. Burton WM. Structure and development of active regions. IAU Symposium No. 35, ed. KO. Kiepenheuer (Dordrecht: Reidel), 1968;393.
3. Tousey R, Sandlin GD, Purcell JD. Structure and Development of Active Regions, 1 AU Symposium No. 35, ed. K. 0. Kiepenheuer (Dordrecht: Reidel), 1968;411.
4. Krieger AS, Timothy AF, Roelof EC. A coronal hole and its identification as the source of a high velocity solar wind stream. Solar Phys. 1973;29(2):505–525.
5. Huber MCE, Foukal PV, Noyes RW, et al. Extreme ultra-violet observations of coronal holes: initial results from Skylab. Astrophysic J. 1974;194:L115–L118.
6. Nolte JT, Krieger AS, Timothy AF, et al. Coronal holes as sources of solar wind. Solar Physics. 1976;46:303–322.
7. Cranmer S. Coronal holes and the high-speed solar wind. Space Science Reviews. 2002;101(3):229–294.
8. Cranmer S. Coronal holes, Living Rev Solar Phys. 2009;6:3.
9. Lukianova R, Holappa L, Mursula K. Centennial evolution of monthly solar wind speeds: Fastest monthly solar wind speeds from long-duration coronal holes. J Geophys Res Space Physics. 2017;122(3):2740–2747.
10. Einaudi G, Boncinelli P, Dahlburg RB, et al. Formation of the slow solar wind in a coronal streamer. J Geophysic Res. 1999;14(A1)521–534.
11. Ofman L. The origin of the slow solar wind in coronal streamers. Adv Sp Res. 2004;33(5):681–688.
12. Bravo S, Stewart GA. Fast and slow wind from solar coronal holes. Astrophysical Journal. 1997;489(2):992.
13. Sulistiani S, Herdiwijaya D. Solar coronal holes and their geo-effectiveness. J Physic Conf Series. 2019;1127(1):012052.
14. Verbanac G, Vrsnak B, Veronig A, et al. Equatorial coronal holes, solar wind high-speed streams, and their geoeffectiveness. Astronomy and Astrophysics. 2011;526(A20):1–13.
15. Delaboudiniere JP, Artzner GE, Brunaud J, et al. EIT: Extreme-Ultraviolet Imaging Telescope for the SOHO Mission. Solar Physics. 1995;162(1-2):291–312.
16. Bromage BJI, Alexander D, Breen A, et al. Structure of a large low-latitude coronal hole. Solar Physics. 2000;193(1/2):181–193.
17. Rotter T, Veronig AM, Temmer M, et al. Relation between coronal hole areas on the Sun and the solar wind parameters at 1 AU. Solar Physics. 2012;281(2):793–813.
18. Rotter T, Veronig AM, Temmer M, et al. Real-time solar wind prediction based on SDO/AIA coronal hole data. Solar Physics. 2015;290:1355.
19. de Toma G. Evolution of coronal holes and implications for high-speed solar wind during the minimum between cycles 23 and 24. Solar Phys. 2011;274:195–217.
20. Krista LD, Gallagher PT. Automated coronal hole detection using local intensity thresholding techniques. Solar Phys. 2009;256,87–100.
21. Del Zanna G, Bromage BJI. The Elephant’s Trunk: Spectroscopic diagnostics applied to SOHO/CDS observations of the August 1996 equatorial coronal hole. J Geophysic Res. 1999;104(5):9753–9766.
22. Zhao XP, Hoeksema JT, Scherrer PH. Changes of the boot-shaped coronal hole boundary during whole sun month near sunspot minimum. J Geophysic Res. 1999;104(A5):9735–9751.
23. Dobrzycka D, Strachan L, Panasyuk A, et al. Study of the latitudinal dependence of H I Lyman α and 0 VI emission in the solar corona: Evidence for the super-radial geometry of the outflow in the polar coronal holes. J Geophysic Res. 1999;104(A5):9791–9800.
24. Insley JE, Moore V, Harrison RA. The differential rotation of the corona as indicated by coronal holes, Solar Physics. 1995;160(1):1–18.