The presence of the perturbation on the torus around the black hole causes the torus material to be swallowed by the black hole and create a Papaloizou-Pringle Instability (PPI) in a few dynamical times. The growth in an instability and stationary accretion phase reached around the black hole show an indication of the presence of the Quasi-Periodic Oscillation (QPOs). In this paper, we present the 2D numerical hydrodynamical simulations of the torus around the black hole in a fixed space-time on the equatorial plane. We show that m = 1 nonaxisymmetric instability and QPOs are presented for the perturbation which is triggered by increasing the angular velocity of torus in equilibrium. Our results indicate that the perturbed black hole-torus system can be a good candidate to explain the high energetic phenomena observed in the center of the galaxies and Active-Galactic Nuclei (AGN).

Keywords: nonaxisymmetric instability, equatorial plane, galaxies, energetic phenomena, space-time, black hole, hydrodynamical equations

PPI, papaloizou-pringle instability; QPOs, quasi-periodic oscillation; AGN, active-galactic nuclei; GRH, general relativistic hydrodynamical

Many high energy astrophysical phenomena happen in a strong gravitational region close to the compact objects such as around the black holes and neutron stars. In order to understand the physics behind these phenomena happening close to the black hole horizon, we numerically need to solve the general relativistic hydrodynamical equations. Describing the dynamical instability and the power spectrums computed from the numerical simulations would allow us to understand physical mechanics behind the high frequency quasi-periodic oscillation. During the last few decades, the analytic and numerical investigations of the oscillatory modes of the torus around the black hole have been done.^1,2,3,4 These investigations revealed the existing of QPOs for a wide range of the physical parameters such as black hole spin and mass rations of torus and black hole, and also for using the pure general relativistic treatment or Newtonian one with approximate potential functions. In this paper, we report the numerical investigation the response of the black hole-torus system against to the linear and sinusoidal perturbations created by increasing the angular velocity of the stable torus in a moderate amount. We present some preliminary results from the numerical simulations. As a result, such perturbations can help us to understand the physical mechanisms behind the PPI and QPOs created close to the black hole in strong relativistic region.

Equations and initial setups

We have numerically modeled the perturbed black hole-torus system by solving General Relativistic Hydrodynamical (GRH) equation in 2D at equatorial plane in a fixed space-time. We setup the black hole-torus system by using the equation, initial setup of the torus, and boundary conditions used in.^5,6 We assume that the black hole is not rotating. We adapt the perfect fluid equation of state with $\Gamma =4/3$  to mimic the degenerate relativistic electron gas. The outer boundary is located at $r=200M$  and the resolutions used along the radial and angular directions are 3072 and 256, respectively. In order to develop the mode operation, we apply a perturbation to the torus increasing the angular velocity of the initial torus in a moderate amount. The applied perturbations to the angular velocities of the torus are given in Table 1. The variables used in the perturbations are: ${\nu }_p^{\varphi }$  s the new value of the angular velocity after the perturbation, ${\nu }^{\varphi }$ is the angular velocity of the stable torus, ${\nu }_{max}^{\varphi }=0.14699c$ is the maximum angular velocity of the stable torus, r is the radial coordinate. The detailed formulations, setup for initial torus, and the numerical explanations can be found our previous works.^5,6,7

The evolution of the maximum rest-mass density of the torus and its radial location as a function of time are given in Figure 1. It is seen that PPI is presented in all models, CP, S P1, and S P2. The instability grows very fastly and the maximum rest-mass density is approximately constant for model CP after the saturation is succeeded. But, for the other models, after the saturation, the maximum density tries to find a new quasi-equilibrium value. It is also observed in the top panel of Figure 1 that the the instability suddenly grows around the initial position of the torus for models S P1 and S P2 but the torus initially expands outward and later falls toward to the black hole in model CP. In order to reveal the how the sinusoidal perturbation affects the disk dynamic, we plot the different snapshots of the rest-mass density for model S P1 seen in Figure 2. It is seen that the nonlinear effects are more dominant and cause the dissipation of the matter of the torus compared to the model CP, seen also in Figure 1. The matter around the black hole tries to reach a new equilibrium position but it has newer achieved during the evolution of our numerical simulation, exactly. The growth of m = 1 nonaxisymmetric structure is observed and the instability is created. But the spiral wave contains a nonlinearity and it causes to dissipation of the torus‘s matter during the evolution. Therefore, after the saturation of PPI, the amplitude of the m = 1 mode slowly decreases.

Figure 1 Evolution of the normalized maximum density location (top panel) and maximum density (bottom panel) of the torus for models CP, S P1, and S P2.

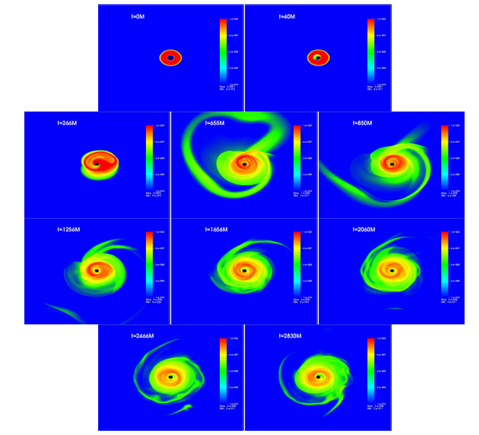
Figure 2 Snapshots of the logarithmic rest-mass density at different times for model S P1. The outer boundary of the each plot are located at $[Xmin,Ymin]\to [Xmax,Ymax]=[-100M,-100M]\to [100M,100M]$ .

The physical mechanisms behind the saturation of the instability in accretion disk or torus around the black hole have still uncertainties. Studying the perturbations in different scales for the torus’s parameters triggers the lower or higher amplitude of the instability.^8,9,10,7 The modification of the angular velocity of the stable torus in a moderate scale plays a crucial role in saturating the instability in torus around the black hole.^5,6 To understand and compare the growing instability in case of the different types of perturbations on the angular velocity of the torus, we plot m = 1 growing mode for linear (model CP) and sinusoidal (models S P1 and S P2) perturbations given in Table 1. As seen in Fig. 3, the first maximum point seen at $t=74M$ in model CP occurs due to linear perturbation applied to the angular velocity of the torus. Later, the nonlinear instability in torus is created and then the growing mode reaches to the saturation point around $t=1200M$ . Here after, the $m=1$  mode strength oscillates around the non-zero fixed value and it is considered that the saturation is successful. We have also perturbed the stable torus by perturbing the angular velocity of the torus with a sinusoidal function given in Table 1. It causes the $m=1$  mode growing with large amplitude, initially and it is saturated around 176M. Just after it reaches to the saturation point, $m=1$  growing mode is disrupted due to the large amount of angular momentum transferring of the disk outward direction, seen in Figure 3 for models S P1 and S P2. Therefore, the saturation does not perfectly successful for the sinusoidal types of perturbations. Our numerical simulations confirm a clear indication of creation of PPI which strongly depends on the types of instability and their strengths.

Figure 3 Evolution of the mode power form m = 1 for all models. The PPI is saturated around t = 1200M and then it shows an oscillation around the non-zero constant value for model CP. The saturations are seen around 176M for models S P1 and S P2 and then the amplitude of the instability is slowly decreasing with time.

The discovering the low and high frequency QPOs around the black hole^11,12 is an important milestone to determine the black hole properties such as the mass and spin. These frequencies can also be used to test the general relativity in the strong field regime. In order to understand what kinds of physical mechanics produce these types of frequencies, we perturb the initially stable tours rotating around the black hole and compute the power spectrum of the system after it reaches to the saturation point. The power spectrums of torus for different models are given in Figure 4. The left panel of Figure 4 shows the occurrence of the fundamental frequency at 93Hz as well as number of overtones at 32Hz, 134Hz, 186Hz, and 208Hz. Once the fundamental frequency is excited, the continues process of the nonlinear coupling of frequency creates the weakly presented new fundamental frequencies and overtones. All frequencies show a good harmonic sequence 1:2:3: .... The strengths of the peaks and their variation can be explained with the value of the maximum density of the initial stable torus and variations in the perturbation applied initially. The fundamental frequency 56Hz and overtones seen in the right panel of Figure 4 for model CP are not in good harmonic sequence like seen in the model S P1. It could be the results of the type of the perturbation used initially. Because the quasi-periodic behavior of the torus is developed depending on the initial kick in the stable torus. While the sinusoidal function with an amplitude (the amplitude various with ${\nu }_{max}^{\varphi }/r^2)$  is used as a perturbation for model S P1, the perturbation which triggers the instability in model CP has a value which varies with the angular velocity of the stable torus (linear perturbation).

Figure 4 Power density spectrum from the mass accretion rate of the quasi-steady state torus rotating around the black hole at radius r = 6.1M for models S P1 and CP. The non-rotating black hole has a mass M = 10M.

We have performed the numerical simulations using three different initial values for angular velocities presented as a perturbation. It is used either linear or sinusoidal perturbation in order to characterize the instability and QPOs of the black hole-torus system. It is found that the spiral mode of PPI grows for linear and sinusoidal perturbations. It survives for a long time around a nonconstant value for linear perturbation after the PPI growth saturation. But the m = 1 structure in the torus does not reach to quasi-equilibrium state for sinusoidal perturbations, exactly. The matter is still accreted toward to the black hole due to the nonlinear forces which exist in torus even in later time of simulation for these perturbations. The black hole-torus system having a PPI is a good candidate to explain the high energetic phenomena. The QPOs produced during theses instabilities may also be used to define the black hole mass.

All simulations were performed using the Phoenix High Performance Computing facility at the American University of the Middle East (AUM), Kuwait.

The author declares there is no conflict of interest.

1. Rezzolla L, Yoshida S, Zanotti O. Oscillations of vertically integrated relativistic tori – I. Axisymmetric modes in a Schwarzschild space-time. MNRAS. 2003;344(3):978–992.
2. Lee, WH, Abramowicz MA, Kluzniak W. Resonance in Forced Oscillations of an Accretion Disk and Kilohertz Quasi-periodic Oscillations. ApJ. 2004;603:L93–L96.
3. Mazur GP, Zanotti O, Sadowski A, et al. Oscillations of radiation pressure supported tori near black holes. MNRAS. 2016;456(3):3245–3252.
4. Parthasarathy V, Manousakisy A, Kluzniakz W. Quasi-periodic oscillations of perturbed tori. MNRAS. 2016;458(1):666–672.
5. Donmez O. Spherical-shell accretion onto the black hole–torus system. MPLA. 2015;30(14):1550071.
6. Donmez O. Angular velocity perturbations inducing the Papaloizou–Pringle instability and QPOs in the torus around the black hole. MPLA. 2017;32(20):1750108.
7. Donmez O. On the development of the Papaloizou–Pringle instability of the black hole–torus systems and quasi-periodic oscillations. MNRAS. 2014;438(1):846–858.
8. Zanotti O, Rezzolla L, Font JA. Quasi-periodic accretion and gravitational waves from oscillating ‘toroidal neutron stars’ around a Schwarzschild black hole. MNRAS. 2003;341(3):832–848.
9. Zanotti O, Font JA, Rezzolla L, et al. Dynamics of oscillating relativistic tori around Kerr black holes. MNRAS. 2005;356(4):1371–1382.
10. Donmez O. The dynamical evolution of the black hole–torus system perturbed by a Bondi–Hoyle accretion. IJMPD. 2014;23(5):1450050.
11. Strohmayer TE. Discovery of a 450 Hz quasi-periodic oscillation from the microquasargro J165540 with therossi X-ray timing explorer. ApJ. 2001;552:L49–L59.
12. Lamb FK. In X-ray Binaries and Gamma-Ray Bursts. In: EPJ van den Heuvel editor. (San Francisco: Astronomy Society of the Pasific). 2014.