The correct scientific and critical analysis of the generally accepted foundations of classical mechanics is proposed. The methodological basis for the analysis is the unity of formal logic and of rational dialectics. The main results of the analysis are as follows: (1) the correct starting point of kinematics is formulated: the informational definition of the concept of time; definitions of the concepts of motion, speed, and acceleration of material point in the metric system of coordinates; the principle of motion of quantum particle (photon); proof of the mathematical, physical, and formal-logical erroneousness (fallaciousness) of Lorentz transformations; (2) the correct starting point of dynamics is formulated: the definition of force as a physical property of the structure of the system of the interacting objects; (3) the correct starting point of the theory of gravitation is formulated: the condition of existence of the gravitational interaction which represents the condition of existence of the region of overlap (superposition, intersection) of the gravitational fields of the material objects; (4) the correct formulation of the law of gravitation within the framework of the system approach is given (the formulation represents the system of the proportions); (5) it is proved that the formulation of Newton’s empirical law of gravitation represents the formal-logical and dialectical errors.

PACS: 01.55.+b, 01.65.+g, 01.70.+w, 02.90.+p, 03.30.+p, 03.65.-w, 04.25.Nx, 45.05.+x, 45.20.-d, 45.20.D-

Keywords: general physics, special relativity, quantum mechanics, classical mechanics, formalisms in classical mechanics, newtonian mechanics, post-newtonian approximation, gravity, philosophy of science, history of science

Recently, the progress of sciences, engineering, and technology has given rise to a new problem: the problem of rationalization of the fundamental sciences (for example, theoretical physics and mathematics). Rationalization of sciences is impossible without rationalization of thinking and critical analysis of the foundations of sciences within the framework of the correct methodological basis: the unity of formal logic and of rational dialectics. Therefore, one should call achievements of classics of sciences in question within the framework of the correct methodological basis. As has been shown in works,^1–99 the foundations of theoretical physics, of mathematics, and of philosophy contain formal-logical and dialectical errors. This signifies that any generally accepted theory can be refuted if it contradicts to the formal-logical and dialectical laws.

As is known,⁹⁸,¹¹⁰ classical mechanics as a branch of physics arose from the needs of sciences and practice and has a long history of development. The important significance of classical mechanics is determined by the contribution of the prominent scientists of past time: Kepler J, Galileo Galilei, Newton I, Lagrange JL, Hamilton WR, and others. Since the end of the 20^th century, the place of classical mechanics in physics has been no longer that of an independent theory. Instead, classical mechanics is now considered an approximate theory to the more general quantum mechanics. Classical mechanics is a theory useful for the study of the motion of non-quantum mechanical, low-energy particles in weak gravitational fields. In the 21^st century classical mechanics has been extended into the complex domain and complex classical mechanics exhibits behaviors very similar to quantum mechanics.

However, the remarkable achievements of the prominent scientists do not signify that the problem of validity of classical mechanics is now completely solved or the foundations of classical mechanics are not in need of analysis within the framework of the correct methodological basis: the unity of formal logic and of rational dialectics. In my opinion, classical mechanics can be considered as a correct theory (scientific truth) if and only if it relies on the correct methodological basis. But there is no formal-logical and dialectical substantiation of classical mechanics in the scientific literature.^98–110

In my opinion, the foundations of classical mechanics are not free from scientific objection. The purpose of this work is to propose the critical analysis of the starting point of classical mechanics. The methodological basis for the analysis is the unity of formal logic and of rational dialectics.

As is known, correct methodological basis of sciences is the unity of formal logic and of rational dialectics. Use the correct methodological basis is a necessary condition for correct analysis to make distinction between truth and falsehood. However, this fact is ignored by majority of scientists until now. Therefore, the main statements of formal logic and of materialistic dialectics which are used in the present work must be stated.

1. The system is a set of elements that are in relations and connections with each other, forming certain integrity, unity.
2. The system principle reads as follows: the properties of the system are not a consequence of the properties of its elements; the system determines the properties of the elements; and the properties of the elements characterize the system.
3. The structure (construction, arrangement, order) is a set of stable connections (bonds) in object, which ensures its integrity and qualitative self-identity (i.e., which ensures the conservation of the basic properties) under different external and internal changes.
4. The system analysis of material system represents a task of finding the states of the material system. This task can be reduced to the task of finding quantitative (tabular or analytical) relationships between the characteristics of the elements of the material system under the condition of conservation of the structure (i.e., qualitative determinacy) of the system. The correct solution of the task should be based on the following practical operations (steps): (a) one chooses the element which must be subjected to a quantitative change (i.e., to a movement); the selected element undergoes the quantitative change without changing in the qualitative determinacy of the system; (b) one finds quantitative changes in other elements under changing in the selected element; these changes should not lead to a change in the structure of the system (i.e., to a change in the qualitative determinacy of the system); (c) one finds the boundaries of quantitative changes within which the system remains identical to itself; (d) one finds the elements which are not changed; (e) one finds a quantitative (tabular or analytic) relationships between the values and dimensions of the variables quantities which characterize elements. However, it should be emphasized that one can obtain an analytical solution of the task only in case of a simple statement of the problem or in the case of simple systems. In these cases, an analytical solution represents a proportion. The proportion represents linear relationship between the relative increments of the quantities describing the different elements.
5. Property is a philosophical category that designates such aspect of material object, which determines difference or commonality between other objects. Property is one of the aspects of the given object or phenomenon. Some properties express the qualitative determinacy of the object, others express the quantitative determinacy of the object;
6. Energy is a general quantitative measure of the quantitative and qualitative changes under interactions of material objects. Energy does not emerge (appear, spring up) from nothing and does not vanish (disappear; exterminate). It can only changes from one values and forms to another. Various (different) forms of energy are as follows: mechanical, internal, electromagnetic, chemical, nuclear and other forms. The law of conservation of energy reads as follows: the energy of an isolated system is conserved:

$E^{(isolatedsystem)}=const$

7. Energy is an inherent (inalienable) physical property of material objects, which characterizes changes in the states of the material objects under interactions of material objects. Energy represents a physical quantity.
8. The material object is a body, a field, a particle, as well as a system of bodies, of fields, of particles.
9. Physical quantity is the unity of qualitative determinacy and of quantitative determinacy of a material object. Mathematics describes the change in the quantitative determinacy of a material object (physical quantity). In terms of formal logic, mathematics does not describe changes in qualitative determinacy of an object.
10. Mathematics studies the quantitative determinacy belonging to the qualitative determinacy of the object. In accordance with formal logic, the left-hand side and right-hand side of the mathematical expression describing the property of a system should be relate and belong to the qualitative determinacy of this system, i.e.,

(the qualitative determinacy of the system) = (the qualitative determinacy of the system).

11. The left-hand side and right-hand side of the mathematical expression describing the property of the element should be relate and belong to the qualitative determinacy of this element, i.e.

(the qualitative determinacy of the element) = (the qualitative determinacy of the element).

12. Both the quantitative and qualitative determinacy of the object must obey logical laws. Therefore, according to the logical law of identity, the left-hand and right-hand sides of the mathematical equation must belong to the same physical object (i.e. to the same property of the physical object or the physical model of the object). And, according to the logical law of lack (absence) of contradiction, the left-hand and right-hand sides of the mathematical equation must not belong to different physical objects (i.e., to different properties, models).
13. The result of mathematical operations on physical quantities must have a physical meaning. Such mathematical operations are called admissible operations.

Mechanics is the science of the mechanical movement and interactions of material bodies. The mechanical interactions represent such actions of bodies on each other, which lead to a change in speeds of these bodies, deformations or attractions of these bodies. Classical mechanics is based on three of Newton’s laws which constitute the basis of mechanics.

The following questions arise: What is the cause (source) movement (as a change)? What are the essential features of the movement as the property of the interaction between the material objects?

Kinematics
As is known, kinematics is the part of mechanics, devoted to the study of the geometrical properties of the motion of material bodies without taking into consideration of their masses and forces acting on them. In other words, kinematics studies motion of material bodies without taking into consideration of causes of the motion. The main task of kinematics is the establishment (determination) of methods of representation of the motion of the material points or of bodies and the determination of the relevant kinematic characteristics of the motions (i.e., trajectory, speed, and acceleration of moving points; the angular velocity and the angular acceleration of the rotating bodies, etc.).

1. The motion of the material point can be given (represented) by one of three mutually complementary ways: vector, coordinate, and trajectory (natural) ways. The coordinate way (coordinate representation) is that the position of the point relative to the coordinate system (reference frame) is determined by certain three coordinates$x$ ,$y$ ,$z$  (i.e., by the Cartesian coordinates $x$ ,$y$ ,$z$ ) and the law of motion is given by three equations (i.e., by $x=x\left(t\right)$ , $y=y\left(t\right)$ , ). If one eliminates variable $z=z\left(t\right)$ height="15" src="PAIJ-02-00066_clip_image017.gif" /> from the equations, one can find the trajectory (i.e., line in the coordinate system) of the moving point. The trajectory (natural) way of describing is used if the trajectory of the moving point relative to the coordinate system (reference frame) is known. The position of the given point is determined by the distance between the reference point selected on the trajectory and the given point on the trajectory (the distance is measured along the trajectory). The law of motion is given by the equation expressing dependence of the traveled (traversed) distance on time:$l=l\left(t\right)$ . The basic kinematic characteristics of a moving point are the speed and acceleration of the point.
2.  Clock $C$  (i.e., a material device created by man) determines time$t$ ; time $t$ characterizes clock$C$ ; time $t$  is a property of clock$C$ . Time $t$  is the universal informational (i.e., non-physical) variable quantity.^{6,13,20,38,48,49} Therefore, time is not a property of natural material objects. The dimension of time is “second (s)”. If $t_0$  and $t_1$ are the values of the variable quantity $t$  (i.e., $t_0$  and $t_1$  are certain points of time), then the difference$\left(t_1-t_0\right)\equiv \Delta t_{10}$ represents the fixed increment of the value of the variable quantity$t$ from the value$t_0$ to the value$t_1$ . The difference $\left(t-t_0\right)\equiv \Delta t_0$  is the variable increment of the value ​​of the quantity $t$ from the value$t_0$ to some other value at that$\Delta t_0\ne 0$ .
3. The Cartesian metric coordinate system $XOY$  is the metric material system formed by the identical material scales $OX$  and $OY$  on the plane.^{50,73,77–81,89,91–94} Scales $OX$ and $OY$  have the dimension of “meter (m)”. The material point $M$  on the plane $XOY$  represents a material object$M$ . The set of possible positions (i.e., the geometrical states) of the object $M$  in the system$XOY$ is called geometric space of the states of the object$M$ . (Description of the positions of the material object $M$  in the system $XOY$ is called geometrical representation (coordinate representation) of the object$M$ ). The material object$M$ and the material system $XOY$  are the independent parts of the whole. Clock $C$  as a material object can be and move in the system$XOY$ . The material object $C$  and the material system $XOY$ are the independent parts of the whole. But time$t$ (as the property of $C$ clock ) does not exist in the system $XOY$ :$t$ does not represent a geometrical (material) object. Scale of time does not belong to the system $XOY$ and does not represent an extension of the system $XOY$  because time has no dimension of “meter (m)”. The quantity which has no dimension of “meter (m)” cannot be graphically represented in the system$XOY$ .^91–94 In other words, the quantity which has no the dimension of “meter (m)” does not exist in the coordinate system$XOY$ .
4. The positions of the material point (i.e., the material object) $M$ on the plane $XOY$  is determined by the coordinates (i.e., by the material projections, the segments of the scales) $x^M$ and$y^M$ which have the dimension of “meter (m)”. (Coordinate is the geometric concept which designates certain segment of the scale. Description of the positions of the material point $M$  in the system $XOY$ is called geometric representation (coordinate representation) of point$M$ ). Material point$M$ exists in the system$XOY$ if and only if the coordinates of point $M$ exists in the system$XOY$ . There are no coordinates in general, but there exist only the coordinates of the material point$M$ . The concepts “positions of material point $M$  on plane$XOY$ ” and “coordinates of material point $M$ on plane$XOY$ ” are identical ones. If point $M$  move on plane$XOY$ , then the coordinates of point$M$ are functions of time:$x^M=x^M\left(t\right)$ ,$y^M=y^M\left(t\right)$ .
5. If clock$C$ is in system$XOY$ and material object $M$ has no effect on the clock mechanism, then property of clock $C$  (i.e., time$t$ ) does not depend on the existence of object$M$ . If property of clock $C$  does not depend on clock positions in system$XOY$ , then time $t$ does not depend on rate of change in positions of the moving clock $C$  in system$XOY$ . Furthermore, time $t$  does not depend on the length of the path traveled by moving clock $C$ in system$XOY$ .
6. If point $M$  is moved on plane$XOY$ , then the positions of the point $M$ characterize the trajectory of the point$M$ : the path (i.e., the material line on plane$XOY$ ) is the locus of the positions of point$M$ . The length of the path (i.e., the length of the segment of line) traveled by point $M$  over (for) time $t$  is$l^M\left(t\right)$ . The concepts of “segment” and “length of line segment” are not identical ones: the segment of the line is a material object, and the length of the segment of the line is a denominate (dimensional) number (i.e., property, the quantitative determinacy of the material object). The line segment exists on plane$XOY$  , but the path length (as length of segment) do not exist on the plane$XOY$ . In other words, there are only geometrical (i.e., material) objects on plane$XOY$ : material points, material lines, and material figures on plane$XOY$ . The path length (i.e., the quantitative determinacy of the line segment) is measured by the use of a device; measurement results are denominate (dimensional) numbers. In other words, the path length exists as a set of denominate (dimensional) numbers. The length $l^M$  of the line segment has the dimension of “meter (m)”, but the quantity $l^M$  has no a graphical representation because $l^M$  is not the material segment of the line on plane$XOY$ . Therefore, the concepts “length of path of point$M$ ” and “coordinates of point$M$ ” is non-identical concepts.
7. The mathematical (i.e., quantitative) quantity $l^M$  has the properties of additivity and multiplicativity, but it is not characterized by the property of directivity on the plane$XOY$ . The property of additivity $l_1^M+l_2^M$  is geometrically (i.e., practically) interpreted as follows: two segments of straight line having lengths $l_1^M$  and $l_2^M$ are coincided with the scale$X$ ; origin of the first segment is coincided with the zero point of the scale $X$ ; the end of the first segment is connected with the origin of the second segment; the length of the connected segments is $l_1^M+l_2^M$ . The property of multiplicatively $l_1^M\times l_2^M$  is practically interpreted as follows: the first segment of straight line having length $l_1^M$  is coincided with the scale$X$ ; origin of the first segment is coincided with the zero point of the scale$X$ ; the second segment of straight line having length $l_2^M$  is coincided with the scale $Y$ ; origin of the second segment is coincided with the zero point of the scale$Y$ ; the area of ​​the rectangle constructed on these segments is $l_1^M\times l_2^M$ ; the quantity of the area does not exist in the system $XOY$ because the quantity of the area has no the dimension of “meter (m)”.
8. Measure of material object$M$ represents the unity of qualitative and quantitative determinacy of object$M$ . The measure of the material object $M$  is invariant under transformation of coordinates. The length of path (i.e., property of line segment, measure of line segment) is invariant under transformation of coordinates. In other words, the length of path is independent of choice of coordinate system. The concepts of “direction”, “direction of motion”, and “vector” in system $XOY$ represent the physical concepts (i.e., qualitative determinacy) and cannot be defined mathematically (i.e., in terms of quantity) in the system$XOY$ .^{65–68,70–75} In physical point of view, there exists a direction of motion. But, in geometric and mathematical points of view, there are only line segments and numbers. The length of the line segment (length of trajectory) is not characterized by a direction of motion, and the direction of motion does not determine the length of path. (Explanation is that the mathematical formalism does not contain motion as change in general. Changes are made by man. Vector is an illustration of direction). Thus, the path length is independent of the direction of the motion of point$M$ .
9. The quantity $l^M\left(t\right)-l^M\left(t_0\right)$  is called increment of the length of the path of point$M$ over (for) time $\Delta t_0\equiv t-t_0$  where$\Delta t_0\ne 0$ , $t_0$ is the initial time. The quantity

$\frac{l^M\left(t\right)-l^M\left(t_0\right)}{\Delta t_0}\equiv v^M\left(\Delta t_0\right)$

Is rate of change in the quantity$l^M$ . In other words, speed of motion of point $M$  is rate of change in quantity$l^M\left(t\right)$  . (Movement is change in general). By definition, the speed of the motion of point $M$ is the average speed over time$\Delta t_0$ . There is no “instantaneous speed” (i.e., speed at point of time$t$ ).⁶⁰ The speed of the motion is the essential feature (property, characteristic) of motion: speed is the rate of the change in number. The rate of the change in the quantity $l^M\left(t\right)$ has no a graphical representation in system$XOY$ because the quantity of the rate has no the dimension of “meter (m)”. The rate of the change in the quantity$l^M\left(t\right)$ is not defined and is not characterized by any direction because the quantity $l^M\left(t\right)$  is not defined and is not characterized by a direction of the motion of the point $M$  in the system$XOY$ . Thus, the rate of the change in the path length is independent of a direction of the motion of the point$M$ .

10. The variable quantity $v^M\left(\Delta t_0\right)$  takes on the values$v_1^M\left(\Delta t_{10}\right)$ ,$v_2^M\left(\Delta t_{20}\right)$ ,$v_3^M\left(\Delta t_{30}\right)$ under $\Delta t_{10}$ , $\Delta t_{20}$ , $\Delta t_{30}$ , respectively. If the interval (duration) of time is the variable quantity$\Delta t_0\equiv t-t_0$ , then the quantity$v^M\left(\Delta t_0\right)$ of the speed is a function of the argument$\Delta t_0\equiv t-t_0$ . The conventional concept of speed at point of time (at instant of time) $t$ (or at point of plane $XOY$ ) has no scientific and practical sense because the speed of the motion is determined by two (different) positions of the moving point $M$ on plane$XOY$ and by two (different) points of time: movement is change in general; but there is no change in position at point of time$t$ (or at point of plane $XOY$ ).
11. If the speed of the motion of point$M$ depends on time, then the quantity $\frac{v^M\left(\Delta t_0\right)-v_1^M\left(\Delta t_0\right)}{\Delta t_0}\equiv a^M$  is called acceleration of the point$M$ on the path length $l^M\left(t\right)-l^M\left(t_0\right)$  where $v_1^M\left(\Delta t_0\right)$  is certain value of speed, which is experimentally determined. Acceleration characterizes the motion of the point$M$ : acceleration is the essential feature (property, characteristic) of the motion of point$M$ . The quantity of the acceleration of the point$M$ has no graphical representation in the system$XOY$ because the quantity of the acceleration has no dimension of “meter (m)”. The quantities $l^M\left(t\right)$ and $a^M$  are connected by the following relationship:$l^M\left(t\right)-l^M\left(t_0\right)=a^M\times {\left(\Delta t_0\right)}^2$ .
12. Coordinate systems$XOY$ and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ represent the identical and mutually independent systems (Figure 1) if: (a) the unity of qualitative and quantitative determinacy of the system $XOY$  is identical with the unity of qualitative and quantitative determinacy of the system$X^{\prime }{O}^{\prime }{Y}^{\prime }$ ; (b) connection between the systems$XOY$  and$X^{\prime }{O}^{\prime }{Y}^{\prime }$  is only information ones. In other words, the coordinate systems$XOY$ and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ are the identical and mutually independent ones if: (a)$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ are the inertial systems; (b) the scales $X$ , $Y$  and $X^{\prime }$ , $Y^{\prime }$  are identical ones; (c) the characteristics of the clocks$C$ and$C^{\prime }$ are identical ones; d) there is no physical interaction between$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ . If coordinate systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ are identical ones, then the system$XOY$ is called “resting” system and the system $X^{\prime }{O}^{\prime }{Y}^{\prime }$  are called “moving” system (Figure 1). System$X^{\prime }{O}^{\prime }{Y}^{\prime }$ is in system$XOY$ . In the case of one-dimensional motion, system$X^{\prime }{O}^{\prime }{Y}^{\prime }$ moves along the scale$X$ . If some material object is in system$X^{\prime }{O}^{\prime }{Y}^{\prime }$ , then this material object is also in system$XOY$ .
13. If the identical systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ does not contain material objects, then the properties of the clocks$C$ and$C^{\prime }$ are identical ones:$C\equiv C^{\prime }$ ,$t\equiv t^{\prime }$ . In this case, the points$O$ and$O\text{'}$ can coincide at$t=t^{\prime }=0$ . If $C\ne C^{\prime }$  and the points$O$  and$O\text{'}$ coincide at$t=0$ , then$t^{\prime }$ can take the value$t^{\prime }=0$ . But, in this case, $t\ne t^{\prime }$  under$t>0$ . If system $XOY$ contains material objects but these material objects have no effect on the clock$C$ , then these material objects have no effect on the clock $C^{\prime }$ as well:$C\equiv C^{\prime }$ , $t\equiv t^{\prime }$ . If material objects have an effect on the clock$C^{\prime }$ only, then$t\ne t^{\prime }$ under$t>0$ . In this case, the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ are non-identical ones. But this contradicts to the condition of identity of the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ . Thus, the condition of identity of the systems$XOY$ and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ leads to the following requirement: $C\equiv C^{\prime }$ , $t\equiv t^{\prime }$ . This requirement represents the requirement of simultaneity of a certain event in the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ .
14. It follows from Figure 1 that

(Length of line segment$x^M$ ) = (length of line segment $x^{O\text{'}}{}^{}$  ) + (length of line segment$x{\text{'}}^M$ )

Where$x^M$ ,$x^{O\text{'}}$  and $x{\text{'}}^M$ are functions of time$t$ . In this case, the following relationships are valid:

(Length of line segment$x^M$ )/$t$  = (length of line segment $x^{O\text{'}}{}^{}$  )/$t$  + (length of line segment$x{\text{'}}^M$ )/$t$ ,
$l^M=l^{O\text{'}}+{l^{\prime }}^M$ , $l^M/t=l^{O\text{'}}/t+{l^{\prime }}^M/t$ ,
$v^M=V^{O\text{'}}+{v^{\prime }}^M$ , ${v^{\prime }}^M=v^M-V^{O\text{'}}$  
$v^M-{v^{\prime }}^M=V^M\equiv V^{O\text{'}}$

Where$v^M$ is the speed of the object $M$ in the system $XOY$ ; ${v^{\prime }}^M$  is the speed of the object $M$  in the system $X^{\prime }{O}^{\prime }{Y}^{\prime }$ ; $V^{O\text{'}}\equiv V^M$  is the speed of the relative motion of the systems $XOY$  and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ ; $V^M\equiv V^{O\text{'}}$  is also the speed of the relative motion of the object $M$  in the systems $XOY$  and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ . These relationships represent the correct formulation of the Galilean principle of relativity, i.e., the principle of relative motion of the classical (macroscopic) objects. These relationships do not impose restrictions on the values of the speeds$v^M$ , ${v^{\prime }}^M$  and$V^{O\text{'}}\equiv V^M$ . The Galilean principle of relativity in the coordinate representation has the following form:

$x^{\prime }{}^M\left(t\right)=x^M\left(t\right)-V^{O\text{'}}t$ ; $V^{O\text{'}}\equiv V^M$ .

This relationship is called Galilean transformation.

15. The motion of the quantum (microscopic) objects differs essentially from the motion of the classical (macroscopic) objects. The principle of relative motion of the quantum (microscopic) object is formulated as follows:^{3–7,21,34,48,49} the translational motion of a free quantum particle is the absolute motion, i.e., the speed of the motion of a free quantum particle does not depend on the choice of reference system because a free quantum particle cannot be at rest. In the case of light (i.e., a set of photons), this principle is formulated as follows: the speed of the light does not depend on the speed of the motion of the source or receiver of the light.
16. If the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ contain the mutually independent physical objects$L$ and$M$ (Figure 1) moving with different speeds, then a description of the motion (kinematics) of the object $L$  in the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$  is similar to the description of motion (kinematics) of the object$M$ under the condition that the object$L$ is not a microscopic object (for example, photon). If the object$L$ represents photon (quantum particle, microscopic object), then the mutually independent objects$L$ (microscopic object) and $M$ (macroscopic object) are non-identical ones:$L\ne M$ because these objects have different qualitative determinacy. But this fact does not lead to violation of the condition of identity of the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ because a photon has no effects on the scales$X$ ,$Y$ ,$X^{\prime }$ ,$Y^{\prime }$ and on the mechanisms of the clocks$C$ ,$C^{\prime }$ . In other words,$C\equiv C^{\prime }$ , $t\equiv t^{\prime }$  also in the case of motion of photon in systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ .
17. The mathematical formulation of the principle of relative motion of photon in the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ has the following form:

$v^L=v\text{'}{}^L$ , $v^L-v\text{'}{}^L\equiv V^L=0$ ; $v^{L}t=v\text{'}{}^{L}t$ ,$l^L={l^{\prime }}^L$

Where $v^L$ and $v\text{'}{}^L$ are the speeds of the motion of photon in the systems $XOY$  and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ , respectively;$l^L$ and ${l^{\prime }}^L$  are the lengths of the paths traveled by the photon in the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ , respectively. These relationships have the following form in the coordinate representation:

$x^L=x^{\prime }{}^L$ , $x^L=v^{L}t$ , $x^{\prime }{}^L=v^{\prime }{}^{L}t$ ;
$v^L=v\text{'}{}^L$ , $v^L-v\text{'}{}^L\equiv V^L=0$ .

Consequently, the correct formula of transformation of coordinates of photon in the systems$XOY$ and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ is as follows:

$x^L\left(t\right)=x^{\prime }{}^L\left(t\right)$ .

The correct formula contains neither$V^{O\text{'}}$  nor$t^{\prime }$ . Thus, the motion of photon (quantum particle) obeys neither the Galilean relativity principle nor the mathematical formulations of the Lorentz relativity principle. This means that the Lorentz transformations represent a logical error.^{3–5,10,19,20,34,38,48,49}

18. As is known, the Lorentz transformations are the result of the following mathematical operations:

1. Substitution of the Galilean transformation (in standard notations),

${x^{\prime }}_M\left(t^{\prime }\right)=x_M\left(t\right)-V_{O\text{'}\text{}}t$ , ${y^{\prime }}_M=y_M$ , ${z^{\prime }}_M=z_M$ ;$V_{O\text{'}}\equiv V_M$ ;$t^{\prime }\ne t$ ,

Into the equation of the front of the light wave in the system $X^{\prime }{O}^{\prime }{Y}^{\prime }$  (in standard notations),

${x^{\prime }}_L^2\left(t^{\prime }\right)+{y^{\prime }}_L^2\left(t^{\prime }\right)+{z^{\prime }}_L^2\left(t^{\prime }\right)=c^2{t^{\prime }}^2$ ; $t^{\prime }\ne t$ ,

Where$cXOY=yq=He9\; q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaqaafaaake\; aajugibiaadogaaaa@3A36@$ is the speed of the light (photons) in the systems and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ ;

2. Finding of the conditions under which the equation of the front of the light wave in the system$X^{\prime }{O}^{\prime }{Y}^{\prime }$ is transformed into the equation of the front of the light wave in the system$XOY$ ,

$x_L^2+y_L^2+z_L^2=c^2{t}^2$ .
The founded conditions are called Lorentz transformations and read as follows: the equation

${x^{\prime }}_L^2+{y^{\prime }}_L^2+{z^{\prime }}_L^2=c^2{t^{\prime }}^2$

Is invariant under the Lorentz transformations. (The concept of “invariance” signifies that the equation describing the wave front has the identical forms in the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ ).

19. Mathematical, physical meanings and logical sense of the Lorentz transformations become apparent in the following simple case. If$x_L\left(t\right)=ct$ , ${x^{\prime }}_L\left(t^{\prime }\right)=\text{}c{t}^{\prime }$  are the equations of the motion of the photon in the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ , respectively, then the substitution of the “Galilean transformation”,${x^{\prime }}_M\left(t^{\prime }\right)=x_M\left(t\right)-Vt$ ,$V\equiv V_{O\text{'}}$ ,$t^{\prime }\ne t$ , into the equations of the motion of the photon means that${x^{\prime }}_M\left(t^{\prime }\right)={x^{\prime }}_L\left(t^{\prime }\right)$ ,$x_M\left(t\right)=x_L\left(t\right)$ . This substitution leads to the following standard relationships:

$x_M-Vt=c{t}^{\prime }$ , $ct-Vt=c{t}^{\prime }$ , $t^{\prime }=t\left(1-\frac{V}{c}\right)$ ,$t^{\prime }=t-\frac{V{x}_L}{c^2}$ .

But, in my view,^{3–5,10,19,20,34,38,48,49} the Lorentz transformations are not free from the following objections.



Figure 1 Coordinate representation of moving material points$L$ ,$M$  and $O\text{'}$ in the inertial systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ . Systems $XOY$  and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ represent “resting” and “moving” systems, respectively;$x$ are coordinates of points.

Objection 1.

In formal-logical point of view, the relationship${x^{\prime }}_M\left(t^{\prime }\right)=x_M\left(t\right)-Vt$ ,$V\equiv V_{O\text{'}}$ ,$t^{\prime }\ne t$ is not the Galilean transformation,${x^{\prime }}_M\left(t\right)=x_M\left(t\right)-Vt$ ,$V\equiv V_{O\text{'}}$ , because${x^{\prime }}_M\left(t\right)\ne {x^{\prime }}_M\left(t^{\prime }\right)$ , i.e.,${x^{\prime }}_M\left(t^{\prime }\right)\ne x_M\left(t\right)-Vt$ ,$V\equiv V_{O\text{'}}$ ,$t^{\prime }\ne t$ .

Objection 2.

In mathematical point of view, the relationships (i.e., substitutions)${x^{\prime }}_M\left(t^{\prime }\right)={x^{\prime }}_L\left(t^{\prime }\right)$ , $x_M\left(t\right)=x_L\left(t\right)$ signify intersection of non-identical mathematical objects (i.e., equations) at any point of time. In physical point of view, these relationships signify: (a) coincidence of the mutually independent and non-identical material objects$M$ and$L$ (which are moved at different speeds!) at any point of time; (b) formation of the system$M+L$  (i.e., formation of bond, formation of connection, formation of the material unity of objects$M$ and $L$ ). In other words, the coincidence means that the coincident (bonded, connected) objects$M$ and $L$ are moved at different speeds at any point of time. But this contradicts to actual practice and, therefore, formal logic. In addition, it is contrary to the condition that the material objects$M$ and$L$ is mutually independent ones.

Objection 3.

By the condition, the systems$XOY$ and$X^{\prime }{O}^{\prime }{Y}^{\prime }$ are identical ones:$t=t^{\prime }$ . But the substitution${x^{\prime }}_M\left(t^{\prime }\right)={x^{\prime }}_L\left(t^{\prime }\right)$ , $x_M\left(t\right)=x_L\left(t\right)$ , $t^{\prime }\ne t$  leads to the following relationship:

$t^{\prime }=t\left(1-\frac{V}{c}\right)$ , $t^{\prime }\ne t$ .

This relationship contradicts to the condition of identity of the systems $XOY$  and $X^{\prime }{O}^{\prime }{Y}^{\prime }$ : $t=t^{\prime }$ . Really, the relationship $t^{\prime }\ne t$ signifies connection of the independent material objects$M$  and$L$ . Thus, formal-logical error is that the binding (connecting, conjunction) of the independent material objects $M$ and $L$  leads to the effect (action) on the clock$C^{\prime }$ in the system$X^{\prime }{O}^{\prime }{Y}^{\prime }$ and does not lead to the effect (action) on the clock$C$ in the system$XOY$ .

The above objections lead to the following conclusion: the standard mathematical formulation of the Lorentz principle of relativity (i.e., the Lorentz transformations) is mathematical, physical, and formal-logical errors. The only correct formulation of the principle of relative motion of light in the coordinate representation is as follows:

${x^{\prime }}_L^{}\left(t^{\prime }\right)=x_L\left(t\right)$ , ${y^{\prime }}_L^{}\left(t^{\prime }\right)=y_L\left(t\right)$ , ${z^{\prime }}_L^{}\left(t^{\prime }\right)=z_L\left(t\right)$ , $t^{\prime }=t$ ; ${v^{\prime }}_L=v_L\equiv c$ .

Thus, the Lorentz transformations – the essence of the special theory of relativity – represent the gross error.^{3–5,10,19,20,34,38,48,49} Elimination of this error leads inherently to the abolition of the special theory of relativity.

Dynamics
As is known, dynamics is the part of mechanics devoted to the study of the motion of the bodies under action of the forces applied to them. In other words, dynamics studies the motion of the material bodies, taking into consideration of the cause of the motion (i.e., interaction between the bodies). The quantity of the interaction between the bodies is measured by the use of a dynamometer. (Dynamometer is the device for measurement of force, consisting of the force link (elastic element) and measuring indicator). The basic concepts of dynamics are mass and force.

1. Mass is the essential (fundamental) physical property (essential feature) of a material object: mass$m$ is the amount of matter in the material object. The dimension of the mass is “kilogram (kg)”. Mass is an additive physical quantity. The property of additivity of mass$m^M$ of material object$M$ is expressed by the following relationship:$m^M=m_1^M+m_2^M$ . Where$m_1^M$ and $m_2^M$ are the masses of the parts of the object$M$ . Mass is not a multiplicative quantity: mass has no multiplicative property. Therefore, the expression $m_1^M\times m_2^M$  has no physical meaning and is an inadmissible expression in science.
2. Mass of a macroscopic object$M$ does not depend on the positions of the object$M$ in the system$XOY$ . Therefore, the mass of the macroscopic object$M$ is independent of the rate of change in the positions of the object$M$ in the system$XOY$ . The principle of independence of mass of macroscopic object$M$ on the speed of the object$M$ is formulated as follows: the mass and speed of the object$M$ are mutually independent physical quantities. There is no logical relation between the concepts of mass and speed of object$M$ : these concepts are incomparable ones. Therefore, the dependence of mass on the speed of the object $M$ in the special theory of relativity (Lorentz transformations) represents a formal-logical error. ^{3–5,10,19,20,34,38,48,49}
3. The product of mass and speed of the moving object$M$ represents the essential physical property (essential feature) of the moving material object:

$p^M\left(\Delta t_0\right)\equiv m^M\times v^M\left(\Delta t_0\right)$

Where the physical quantity $p^M\left(\Delta t_0\right)$  is called momentum of object$M$ . The dimension of the quantity of the momentum is$kgm{s}^{-1}$ . This definition of the momentum satisfies the formal-logical law of identity:

(Property of the moving object$M$ ) = (property of the moving object$M$ ).

In addition, the definition of the momentum satisfies the formal-logical law of lack (absence) of contradiction:

(Property of the moving object$M$ ) $\ne$ (Property of the moving object$non-M$ )

5. The rate of change in the momentum of the moving object $M$  represents the essential physical property (essential feature) of the motion of the material object. The rate of change in the momentum of the moving object$M$ is defined as follows:

$\frac{p^M\left(\Delta t_0\right)-p_1^M\left(\Delta t_0\right)}{\Delta t_0}=m^M\times \frac{\left[v^M\left(\Delta t_0\right)-v_1^M\left(\Delta t_0\right)\right]}{\Delta t_0}$ ,

$\frac{p^M\left(\Delta t_0\right)-p_1^M\left(\Delta t_0\right)}{\Delta t_0}=m^M\times a^M$

Where $p_1^M\left(\Delta t_0\right)$  is a certain value of the momentum, which is determined experimentally? The dimension of the quantity of the rate of change in the momentum is$kgm{s}^{-2}$ . The dimension $kgm{s}^{-2}$ characterizes the qualitative determinacy of the quantity of rate of change in the momentum. The definition of the rate of change in the momentum of the moving object satisfies the formal-logical law of identity:

(Property of the moving object$M$ )= (property of the moving object$M$ ).

In addition, the definition of the rate of change in the momentum satisfies the formal-logical law of lack (absence) of contradiction:
(Property of the moving object$M$ ) $\ne$ (property of the moving object $non-M$ )

7. The interacting material objects represent a system. Force is the cause of changes in the system. Force is an essential physical property (essential feature, characteristics) of the material interaction of the objects. Force is a physical property of the structure (i.e., of the material connection of the elements) of the system. The qualitative determinacy of the structure (i.e., of the material connection) is not identical with the qualitative determinacy of the elements of the system. Therefore, the property of the structure (i.e., the property of the material connection) is not identical with the property of any element of the system. In other words, force (as the property of the material connection between of the interacting objects) does not represent a property of the interacting objects. The quantity of force is measured by the use of a dynamometer and has the dimension of “kilogram-force (kgf)”. The dimension of “kilogram-force (kgf)” characterizes the qualitative determinacy of force (i.e., of the structure of the system). The dimension of “kilogram-force (kgf)” is the universal and independent dimension of force: this dimension does not depend on the type of interaction and cannot be reduced to another dimension.
8. If: (a) two material objects$N$ ,$M$  and material connection$D$ between objects$N$ ,$M$  (i.e.,$D$ connects objects$N$ and$M$ ) represent the system $S=N+D+M$  (where the property of the material connection $D$  is determined (measured) by a dynamometer); (b) the objects$N$ ,$M$ interact in such a way that the object $N$ is the cause of the motion of the object $M$ at an acceleration $a_M$ , –then the relationship between the force$F^D$ (which is measured by the use of a dynamometer) and acceleration$a_M$ represents the following proportion:

$\frac{F^D-F_1^D}{F_1^D}=\frac{a^M-a_1^M}{a_1^M}$ , i.e.,

$F^D=\left(\frac{F_1^D}{a_1^M}\right)\times a^M$ ,$F^D=\left(\frac{F_1^D}{m^M\times a_1^M}\right)\times \left(m^M\times a^M\right)$

Where $F_1^D$  is a certain value of variable quantity$F^D$ , which is the reading of the dynamometer; the quantity $F^D$  characterizes the structure of the system and has the dimension of$kgf$ ; the quantity $\left(m^M\times a^M\right)$  characterizes the element$M$ of the system and has dimension of$kgm{s}^{-2}$ . The dimensions of $kgf$  and $kgm{s}^{-2}$ characterizing the structure and element of the system have different qualitative determinacy and are non-identical ones:

(qualitative determinacy of force) $\ne$ (qualitative determinacy of rate of change in momentum).

Therefore, the concept of force does not represent the system of concepts of “kilogram”, “meter”, and “square second”. In other words, the concept of force and the concept of “rate of change in momentum” are in conflict with each other.

9. The correct relationships between quantity of force and some other physical quantities (such as length, mass, speed of material object) represent the proportions by quantity of force and some other physical quantities:

$\frac{F^D-F_1^D}{F_1^D}=\frac{l^M-l_1^M}{l_1^M}$ ,

$\frac{F^D-F_1^D}{F_1^D}=\frac{v^M-v_1^M}{v_1^M}$ ,

$\frac{F^D-F_1^D}{F_1^D}=\frac{m^M-m_1^M}{m_1^M}$ .

Thus, force is a property of the material structure of the system of the material elements (material objects). This property of structure does not depend on the properties of the elements of the system (Figure 2).

10. Force as a property of the material connection of the elements of the system of the interacting objects can be depicted as follows. The force of the interaction between two objects$N$  and $M$ is depicted as straight-line segment with two arrows at the endpoints. The two arrows show (indicate) the directions of the force. The endpoints of the segment represent the two points of application (apposition) of the force of the interaction: one end shows (indicates) the point of application (apposition) of the force to the object$N$ , the other end shows (indicates) the point of application (apposition) of the force to the object$M$ . The segment with only one point of application (apposition) of force and with only one arrow does not represent force in general and the force of the interaction because such segment has no physical meaning: force is always the force of the interaction. In other words, the interaction force is a single force,

$F^{NM}\equiv F^{MN}\text{}\equiv F^{(\mathrm{int}eraction)}$ ,

Which cannot be decomposed into two independent (opposite) components: the action force$F^{(action)}$ and the counteraction force$F^{(counteraction)}$ . The action force does not exist without the counteraction force; the counteraction force does not exist without the action force.

Mathematical expression
$F^{NM}-F^{MN}\equiv 0$

Signifies the complete extermination (or absence) of the interaction force, i.e.,

$F^{(\mathrm{int}eraction)}\equiv 0$ .

Therefore, the standard relationship
${\overrightarrow{F}}^{(action)}=-{\overrightarrow{F}}^{(counteraction)}$

Represents an error.

11. In the dialectical point of view, the force of the interaction of the material objects$N$ and $M$ represents the unity of opposite aspects: action and counteraction. The unity of opposites does not mean the identity of opposites because opposites have different qualitative determinacy.
12.  In formal-logical point of view, the concepts of “action” and “counteraction” are dissenting concepts. There are no relation of identity, relation of subordination, and relation of partial coincidence between these concepts. The logical relation between the concepts of “action” and “counteraction” is the relation of disagreement: one concept eliminates another concept; both the concepts cannot be applied to the same objects. (For example, the concept of “action” characterizes the active object$N$ , the concept of “counteraction” characterizes counteracting object$M$ ). These concepts are subordinate and contradictory ones: the scopes (volumes) of these two concepts enter into the scope of another – more general – concept of “interaction” as a “unity of opposites”. Therefore, the concepts of “action” and “counteraction” are connected by the formal-logical law of lack (absence) of contradiction:

(action) $\ne$ (counteraction).

The relationship

$F^{NM}\equiv F^{MN}\text{}\equiv F^{(\mathrm{int}eraction)}$

Satisfies the formal-logical law of identity:

(interaction force) = (interaction force).

Consequently, the standard assertion that

(action force) = (interaction force)

Represents violation of the formal-logical law of lack (absence) of contradiction. Thus, Newton's doctrine of force is incorrect.

The law of gravitational interaction

If interaction between material objects$A$  and$B$ represents the gravitational interaction, then one must consider the complete system $S=A+G^{AB}+B$  (Figure 3) within the framework of the system approach (i.e., within the framework of the unity of formal logic and of rational dialectics).

The system analysis consists in the following steps: detection of the elements of the system; detection of the connections between the elements; and finding of relationships between the physical quantities characterizing elements and connections.

1. Physical quantities relating to Figure 3 are defined as follows:


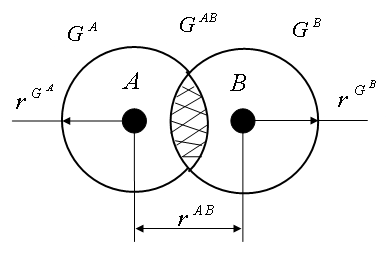
Figure 3 The gravitational interaction of the macroscopic objects $A$ and$B$ . Material objects $G^A$ and $G^B$ are the gravitational fields of the objects$A$ and$B$ ; material object $G^{AB}$ (shaded region) is the region of the overlap of the gravitational fields $G^A$  and$G^B$ .

1. The macroscopic material objects$A$ and$B$ represent the elements of the complete system $S=A+G^{AB}+B$ ;
2. $r^{AB}$  is the distance between macroscopic objects$A$ and$B$ ;
3. The macroscopic material objects $G^A$  and $G^B$  are the gravitational fields of the objects$A$ and$B$ , respectively;
4. $r^{G^A}$ and $r^{G^B}$  are the radii of the gravitational fields $G^A$  and $G^B$ , respectively;
5. The relationship $r^{AB}<r^{G^A}+r^{G^B}$ is a necessary condition for the gravitational interaction;
6. The macroscopic material object $G^{AB}$ (i.e., the shaded region) represents the region of the overlap of the gravitational fields $G^A$ and $G^B$ ;
7. $G^{AB}$  is the structure of the system; (in other words, $G^{AB}$  is the material element which connects the objects$A$ and$B$ );
8. $G^{AB}$  is a carrier of the gravitational interaction (the force interaction);
9. The force of the interaction is a property of the structure$G^{AB}$ .
2. The relationships between the physical quantities characterizing elements and connections in the complete system $S=A+G^{AB}+B$  can be defined in the following heuristic way:
1. The force interaction between the material objects $A$  and $B$  exist if $r^{AB}<r^{G^A}+r^{G^B}$ ; the force interaction between the material objects$A$ and$B$ do not exist if $r^{AB}>r^{G^A}+r^{G^B}$ ;
2. Mass is a property (attribute) of the gravitational field; the gravitational fields$G^A$ and$G^B$ are characterized by the masses$m^{G^A}$ and $m^{G^B}$ ;
3. The masses$m^{G^A}$ and $m^{G^B}$ of the gravitational fields$G^A$ and$G^B$ are directly proportional to the masses$m^A$ and $m^B$ of the objects$A$ and$B$ , respectively;
4. The mass$m^{G^{AB}}$ of the region of overlap of the gravitational fields $G^A$  and $G^B$ is directly proportional to the sum $\left(m^A+m^A\right)$ :

$m^{G^{AB}}\propto \left(m^A+m^B\right)$ ;

5. The mass $m^{G^{AB}}$ increases under decrease of the distance$r^{AB}$ :

$m^{G^{AB}}\propto \exp \left(-\frac{r^{AB}}{r^{G^A}+r^{G^B}}\right)$ .

(Remark: Inverse proportional function$y=1/x$ is not manifested (i.e., graph does not exist) in the metrical system $XOY$ because$y$ has no dimension of length (“meter”) if $x$ have the dimension of length (“meter”).^89–94 In addition, $y$  is an unbounded function which has no physical meaning);

6. The force $F^{G^{AB}}$  of the gravitational interaction is directly proportional to the mass $m^{G^{AB}}$ :

$F^{G^{AB}}\propto m^{G^{AB}}$

3. Within the framework of the system approach, the heuristic assertions lead to the following system of three proportions:

$\frac{F^{G^{AB}}-F_1^{G^{AB}}}{F_1^{G^{AB}}}=\frac{m^{G^{AB}}-m_1^{G^{AB}}}{m_1^{G^{AB}}}$ ;

$\frac{F^{G^{AB}}-F_1^{G^{AB}}}{F_1^{G^{AB}}}=\frac{\left(m^A+m^B\right)-\left(m_1^A+m_1^B\right)}{\left(m_1^A+m_1^B\right)}$ ;

$\frac{F^{G^{AB}}-F_1^{G^{AB}}}{F_1^{G^{AB}}}=\frac{\exp \left(-\frac{r^{AB}}{r^{G^{{}^A}}+r^{G^{{}^B}}}\right)-\exp \left(-\frac{r_1^{AB}}{r_1^{G^A}+r_1^{G^B}}\right)}{\exp \left(-\frac{r_1^{AB}}{r_1^{G^A}+r_1^{G^B}}\right)}$ ,

Where:
$F_1^{G^{AB}}$ is a certain value of the force of the gravitational interaction;
$m_1^{G^{AB}}$ is a certain value of the mass of the region$G^{AB}$ of the gravitational interaction;
$m_1^A$ and$m_1^B$ are certain values of the masses of the objects$A$  and $B$ , respectively;
$r_1^{AB}$ is a certain value of the distance between the objects$A$  and $B$ ;
$r_1^{G^A}$ and$r_1^{G^B}$  are certain values of the radii of the gravitational fields of the objects$A$  and $B$  respectively.

These values of the physical quantities are determined experimentally. The system of the proportions represents a system of mutually complementary relationships which satisfy the formal-logical and dialectical laws.

4. The system of the proportions leads to the following system of three mutually complementary (mutually additional) mathematical formulations of the law of gravitation:

$F^{G^{AB}}=\left(\frac{F_1^{G^{AB}}}{m_1^{G^{AB}}}\right)m^{G^{AB}}$ ,

$F^{G^{AB}}=\left(\frac{F_1^{G^{AB}}}{m_1^A+m_1^B}\right)\left(m^A+m^B\right)$ ,

$F^{G^{AB}}=\left[\frac{F_1^{G^{AB}}}{\exp \left(-\frac{r_1^{AB}}{r_1^{G^A}+r_1^{G^B}}\right)}\right]\exp \left(-\frac{r^{AB}}{r^{G^A}+r^{G^B}}\right)$ .

The law of gravity can be expressed in the following equivalent form:

$F^{G^{AB}}=\left(\frac{F_1^{G^{AB}}}{m_1^{G^{AB}}}\right)m^{G^{AB}}$ ,

$m^{G^{AB}}=\left(\frac{m_1^{G^{AB}}}{m_1^A+m_1^B}\right)\left(m^A+m^B\right)$ ,

$m^{G^{AB}}=\left[\frac{m_1^{G^{AB}}}{\exp \left(-\frac{r_1^{AB}}{r_1^{G^A}+r_1^{G^B}}\right)}\right]\exp \left(-\frac{r^{AB}}{r^{G^A}+r^{G^B}}\right)$ .

Remark: The system of the proportions is analogous (but not identical) to the following differential form:

$dF\left(M,R\right)={\left(\frac{\partial F}{\partial M}\right)}_{R}dM+{\left(\frac{\partial F}{\partial R}\right)}_{M}dR$

Where$M\equiv m^A+m^B$ , $R\equiv r^{AB}$  are the arguments of the function$F=F\left(M,R\right)$ . The difference between the differential form and the system of the proportions is that the differential and integral calculus is a false theory). ^{52–55,57,61,89,90‒94}

5. As is well known, the empirical formulation of Newton’s law of gravitation is as follows:

$F^{AB}=\gamma \frac{m^A{m}^B}{\left(r^{AB}\right){\text{}}^2}$

Where$\gamma$ is the gravitational constant. But Newton’s formulation is not free from the following objections:

1. The quantity $\left(m^A{m}^B\right)$ has no physical meaning because: the quantity$\left(m^A{m}^B\right)$ does not represents a property (feature) of material object; in accordance with practice, mass of an object is a additive (not multiplicative) quantity;
2. Quantities$1\text{}/\left(r^{AB}\right)$ and${1\text{}/\left(r^{AB}\right)}^2$ are not manifested (i.e., graph does not exist) in the metrical system $XOY$ ^89–94 because these quantities have no dimension of length (“meter”); quantity ${\left(r^{AB}\right)}^2$  is an area of the surface of non-existent material object. (What is this material object?). But the area of a surface does not characterize a distance.

Thus, Newton’s law of gravitation is incorrect because it does not satisfy the formal-logical and dialectical laws