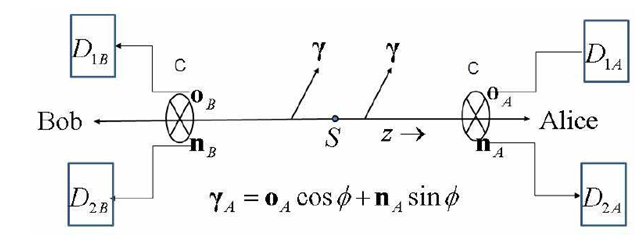The paper which introduced such notions as “weak measurements” and “weak values” is shown to be wrong. The correct description of the considered Stern Gerlach experiment is given. Some experimental works based on are criticized. Some other respectable pseudo sciences are also mentioned. In between them are EPR and EPRB paradoxes, Quantum cryptography, teleportation, computers, and researches about Kochen-Specker theorem. A scientific censorship against critical papers is demonstrated. Some real problems of Quantum Mechanics (QM) are listed.

Keywords: optics, polarization, stern-gerlach experiment, interference, weak measurements, weak value, entanglement, EPR paradox, bell’s inequalities

It, seems, not appropriate to criticize scientific papers strongly. Though they can contain some errors and not well based claims, you are permitted to point out defects only softly, because you are sure that defects in scientific papers are always accident. But, if some work, like that by Aharonov Y et al.,¹ with poor mathematics and “discovery” of physically absurd value, is accepted by many physicist as afflatus, if they even perform experiments based on “weak measurements” with “mind-boggling” precision, it all looks, as if there is a plot against the real science to fool all the scientific community. In such a case it is legitimate to raise a question, how can it happen? The question is like a fight, and the fight is difficult because the pseudo science is originated by respectable people. It is published in respectable journals like Phys. Rev. Lett., Phys. Rev. And others. Moreover, acceptance of fraud means that those groups, whose works were based on this pseudoscience, made no result. However it is necessary to start the fight and here is one of the attempts. Some, not essential, critical remarks against AAV paper were raised in.^2–4 The stronger criticism is given in the work,⁵ which is not published because of scientific censorship. What is readily published is alleluia^6–8 to absurd definition of the ”weak measuring devices”, where it was even said⁷ that “Weak measurement is increasingly acknowledged as one of the most promising research tools in quantum mechanics.”

In this my paper, which has also zero chances to be published, I directly claim that AAV paper is completely wrong, and all the science stemmed from it is the pseudo one. The AAV paper is wrong in mathematics, and in physics, and the introduced in it “weak values” are absurd ones. It is funny to watch how scientific community accepted and developed this pseudoscience. When people cannot formulate a physical problem they want to study, but they want to present their work as one of fundamental importance, they simply include in their experiment some small perturbation, which permits them to declare that they make outstanding “weak measurements”. However it is not a research, it is only a simulation of it.

It is necessary to point out that AAV paper was published in April 4 issue of Phys. Rev. Lett, so the publishers could consider it like an April fool joke. In that case my paper means that I am unable to appreciate how cool AAV paper is. However, I think that it is not a humor but an insult to the scientific community, a firm belief that scientific community is so stupid, that it will swallow everything that is produced by them. And (so funny) they turned out to be right.

Beside the AAV science there are many other pseudo sciences, like EPR paradox, Bell’s inequalities, quantum computers, and quantum cryptography and quantum teleportation. The reason for calling them pseudo sciences is common: they all based on entanglement of far separated particles, and existences of this entanglement have not yet been proved. It is also necessary to point out a crisis appeared in Physics. The job of many scientific groups is aimed at searching for something absent, like electric dipole moment of neutron, with higher and higher precision. Though there are indeed a lot of real problems in QM, which are worth of investigation, nobody tries even to touch them.

Let’s imagine a student’s laboratory experiment of Stern-Gerlach type shown in Figure 1. A beam of polarized particles (let’s call them neutrons), propagating along $y$ -axis, is transmitted through a system of inhomogeneous vertical and horizontal magnetic fields. After transmission its space distribution ${\rho }_z$ is analyzed by position sensitive detectors. The first vertical field is weak, so the beam after it becomes only wider in z-direction, but does not split into two separate parts. The second, horizontal field is strong, and it splits the beam into two separate parts with opposite polarizations $\mathrm{<mo>|</mo>}\pm x\rangle$ . The question is: what information about interaction of the neutron with the first weak vertical field can be extracted from the space distribution ${\rho }_z$ of registered neutrons? Such an experiment does not pose a scientific problem, but it gives an opportunity to calculate dynamics of a neutron in the fields and to compare the result with experimental data. Theoretically it is not a simple job for calculations, because it is necessary to solve the stationary Schrödinger equation with inhomogeneous fields, which are not known precisely enough. The scientists AAV¹ avoided all the difficulties and transformed such a problem into a quantum conundrum by introducing new concepts: “the weak measurements” and “weak values”. Let’s show how they tried to solve the problem.

Figure 1 Outline of the experimental setup. Neutrons pass first through a small vertical inhomogeneous field, where they feel acceleration  and their energy of the vertical motion increases or decreases by an amount $\propto a\delta z$ ($\delta z$ is their vertical shift in the weak field), and further they pass through the strong magnetic field, where the beam splits.

The AAV’s approach to the problem

They described transmission through the small field with gradient along z-axis as the transformation

$\mathrm{<mo>|</mo>}{\Psi }_{\text{f}}\mathrm{<mo\; stretchy="false">(</mo>}p\mathrm{<mo\; stretchy="false">)</mo>}\rangle \mathrm{<mo>=</mo>}\exp \left(-i{\displaystyle \int }H\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}dt\right)\mathrm{<mo>|</mo>}{\Psi }_{\text{i}n}\mathrm{<mo\; stretchy="false">(</mo>}p\rangle \mathrm{<mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}i\gamma q\widehat{A}\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\Psi }_{\text{i}n}\mathrm{<mo\; stretchy="false">(</mo>}p\rangle \mathrm{,}$             (1)

Where the Hamiltonian H(t) is $-g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}q\widehat{A}$ , $q$ is a position operator canonically conjugated to momentum $p$ , $g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ is some function of transmission through the z-field such, that ${\displaystyle \int }dtg\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\gamma$ characterizes weakness of the z-field,

$\mathrm{<mo>|</mo>}{\Psi }_{\text{i}n}\mathrm{<mo\; stretchy="false">(</mo>}p\mathrm{<mo\; stretchy="false">)</mo>}\rangle \mathrm{<mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}-p^2\mathrm{<mo>/</mo>4}{\Delta }^2\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle$         (2)

Is the initial wave function with the spinor part $\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle$ , which is a superposition of eigen states $\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>=</mo>}{a}_i\rangle$ of the operator $\widehat{A}$ in the Hamiltonian with eigen values $a_i$ :

$\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo>}{\displaystyle \sum _i}{\alpha }_i\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>=</mo>}{a}_i\rangle \mathrm{.}$              (3)

Substitution of (2) and (3) into (1) gives

$\exp \mathrm{<mo\; stretchy="false">(</mo>}i\gamma q\widehat{A}\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\Psi }_{\text{i}n}\mathrm{<mo\; stretchy="false">(</mo>}p\rangle \mathrm{<mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}p-\gamma \widehat{A}\mathrm{<mo\; stretchy="false">)</mo>}}^2\mathrm{<mo>/</mo>4}{\Delta }^2\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo>}{\displaystyle \sum _i}\exp \mathrm{<mo\; stretchy="false">(</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}p-\gamma a_i\mathrm{<mo\; stretchy="false">)</mo>}}^2\mathrm{<mo>/</mo>4}{\Delta }^2\mathrm{<mo\; stretchy="false">)</mo>}{\alpha }_i\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>=</mo>}{a}_i\rangle \mathrm{.}$             (4)

This result, in fact, is not acceptable because of energy non conservation. The composition of two fields does not vary with time, and, if there are no external fields before and after installation, which is presumed, then one can expect energy conservation for every spin component with the initial momentum $p$ . For AAV the solution (4) is also not acceptable, but because of different reason. They do not like that the change of energy is too small, when $\gamma$ is small. Therefore they decided to make an enhancement. They invented the enhancement not with installation, but on paper.

A genuine trick

From (1) one can calculate the probability amplitude to find spinor state $\mathrm{<mo>|</mo>}{\psi }_{\text{f}}\rangle$ in the final wave function. It is proportional to

$\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}i\gamma q\widehat{A}\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle \approx \langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>1}+i\gamma q\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo>}\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle +i\gamma q\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{.}$        (5)

AAV made a genuine trick. They continued (5) as follows

$\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle +i\gamma q\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo>}\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle \left(1+i\gamma q\frac{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle }{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }\right)\mathrm{<mo>=</mo>}\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle \exp \mathrm{<mo\; stretchy="false">(</mo>}i\gamma q{A}_w\mathrm{<mo\; stretchy="false">)</mo>,}$     (6)

Where $A_w$ is the introduced so called “weak value”:

$A_w\mathrm{<mo>=</mo>}\frac{\langle {\psi }_f\mathrm{<mo>|</mo>}A\mathrm{<mo>|</mo>}{\psi }_i\rangle }{\langle {\psi }_f\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_i\rangle }\mathrm{,}$ (7)

This is absurd, because it can be any large, when the denominator is small. So (7) has no physical meaning, but because of¹ it had now acquired a name, and because of publication in a respectable journal, it had became accepted very seriously by the scientific community. The AAV work now is cited as a “seminal”,^6,9 even landmark¹⁰ one, and the “weak values” are accepted as a “whole new window into the quantum world”.¹⁰

For not to have $A_w$ too large the choice of orthogonal initial and final states is forbidden, and some experimenters take this restriction seriously though frequently violate. After substitution of (7) the Equation (1) with account of (6) gives

$\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}i\gamma q\widehat{A}\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\Psi }_{\text{i}n}\mathrm{<mo\; stretchy="false">(</mo>}p\mathrm{<mo\; stretchy="false">)</mo>}\rangle \mathrm{<mo>=</mo>}\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle \exp \mathrm{<mo\; stretchy="false">(</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}p-\gamma A_w\mathrm{<mo\; stretchy="false">)</mo>}}^2\mathrm{<mo>/</mo>4}{\Delta }^2\mathrm{<mo\; stretchy="false">)</mo>.}$         (8)

It is not harmful if $\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle$ is small. To overcome the smallness one needs only to conduct an experiment a little bit longer to acquire sufficient number of neutrons.

A generalization to “super weak measurement”

Equation (6) can be easily generalized as follows

$\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle +i\gamma q\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo>}{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2\left(\frac{1}{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }+i\gamma q\frac{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle }{{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2}\right)\mathrm{<mo>=</mo>}$

$\mathrm{<mo>=</mo>}{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2\left(\frac{1}{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }-1+1+i\gamma q\frac{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle }{{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2}\right)\mathrm{<mo>=</mo>}{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2\left(\frac{1}{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }-1\right)+$

$+{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2\left(1+i\gamma q\frac{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo>}\widehat{A}\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle }{{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2}\right)\approx {\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2\exp \mathrm{<mo\; stretchy="false">(</mo>}i\gamma q{A}_{sw}\mathrm{<mo\; stretchy="false">)</mo>,}$    (9)

Where

$A_{sw}\mathrm{<mo>=</mo>}\frac{\langle {\psi }_f\mathrm{<mo>|</mo>}A\mathrm{<mo>|</mo>}{\psi }_i\rangle }{{\langle {\psi }_f\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_i\rangle }^2}$                                     (10)

Is a “superweak value”, and the first term in the right hand side of (9) with the wise choice of “pre and post selected” states can be neglected because it is small

${\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2\left(\frac{1}{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }-1\right)\mathrm{<mo>=</mo>}\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle -{\langle {\psi }_{\text{f}}\mathrm{<mo>|</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle }^2\ll \mathrm{1,}$                    (11)

And it gives a constant background which with sufficient number of neutrons can be easily excluded from the measured effect. With the superweak value one can measure shifts¹¹ of the order of femtoAngstrom and rotation angles¹² of the order of attoradians. Of course, the generalization can be generalized even more too super super weak value and so on, which demonstrates complete absurdity of this way enhancement.

How calculations with a weak stern-gerlach field can be done

All the calculations presented in¹ are irrelevant. Let’s show how they can be done. The first weak magnetic field can be modelled by a thin film of thickness $l$ with magnetic interaction $az{\sigma }_z$ . Where $a\mathrm{<mo>=</mo>}-dB\mathrm{<mo>/</mo>}dz$ is the neutron acceleration in the inhomogeneous magnetic field directed along $z$ -axis. Transformation of the neutron WF

$\mathrm{<mo>|</mo>}{\Phi }_{\text{i}n}\mathrm{<mo\; stretchy="false">(</mo>}p\mathrm{,}r\mathrm{<mo\; stretchy="false">)</mo>}\rangle \mathrm{<mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}ikr-i\omega t\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle$                                      (12)

Can be considered quasi classically. Suppose that the neutron with the wave vector along $k$ -axis enters the film at some point $z$ . Then it will be accelerated up or down, and during the time $t\mathrm{<mo>=</mo>}l\mathrm{<mo>/</mo>}k$ of passage through the film it will shift the distance $\delta z\mathrm{<mo>=</mo>}\pm a{l}^2\mathrm{<mo>/</mo>2}{k}^2$ and acquire component $k_z$ of the wave vector in $z$ direction equal to $k_z\mathrm{<mo>=</mo>}al\mathrm{<mo>/</mo>}k$ . At the exit from the film, the neutron will lose the energy $ma\mathrm{<mo>|</mo>}\delta z\mathrm{<mo>|</mo>}$ . Therefore its wave number in $y$ direction becomes $k_y\mathrm{<mo>=</mo>}\sqrt{k^2-2a\mathrm{<mo>|</mo>}\delta z\mathrm{<mo>|</mo>}}\mathrm{<mo>=</mo>}\sqrt{k^2-{\mathrm{<mo\; stretchy="false">(</mo>}al\mathrm{<mo>/</mo>}k\mathrm{<mo\; stretchy="false">)</mo>}}^2}$ . One can see that in the stationary WF the total energy $k^2\mathrm{<mo>/</mo>2}$ after transmission through the weak field does not change. For an arbitrary initial (preselected is a redundant terminology) polarization state

$\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo>}\alpha \mathrm{<mo>|</mo>}+z\rangle +\beta \mathrm{<mo>|</mo>}-z\rangle \mathrm{,}$        (13)

Where $\mathrm{<mo>|</mo>}\alpha {\mathrm{<mo>|</mo>}}^2+\mathrm{<mo>|</mo>}\beta {\mathrm{<mo>|</mo>}}^2\mathrm{<mo>=</mo>1}$ and $\mathrm{<mo>|</mo>}\pm z\rangle$ are eigen spinors of the Pauli matrix ${\sigma }_z$ with eigenvalues $\pm 1$ , the WF after transmission of the film with weak inhomogeneous field is representable as

$\mathrm{<mo>|</mo>}{\psi }_1\rangle \mathrm{<mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}i{k}_{1}y\mathrm{<mo\; stretchy="false">)</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}i{k}_z{\sigma }_{z}z\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}i{k}_{1}y\mathrm{<mo\; stretchy="false">)</mo>}\left[\alpha \mathrm{<mo>|</mo>}z\rangle \exp \mathrm{<mo\; stretchy="false">(</mo>}i{k}_{z}z\mathrm{<mo\; stretchy="false">)</mo>}+\beta \mathrm{<mo>|</mo>}-z\rangle \exp \mathrm{<mo\; stretchy="false">(</mo>}-i{k}_{z}z\mathrm{<mo\; stretchy="false">)</mo>}\right]\mathrm{.}$          (14)

Since

$\mathrm{<mo>|</mo>}\pm z\rangle \mathrm{<mo>=</mo>}\frac{1}{\sqrt{2}}\mathrm{<mo\; stretchy="false">[</mo><mo>|</mo>}x\rangle \pm \mathrm{<mo>|</mo>}-x\rangle \mathrm{<mo\; stretchy="false">]</mo>,}$          (15)

The WF after separation by the strong field in horizontal $x$ -direction becomes

$\mathrm{<mo>|</mo>}{\psi }_f\rangle \mathrm{<mo>=</mo>}\frac{1}{\sqrt{2}}\exp \mathrm{<mo\; stretchy="false">(</mo>}i{k}_{1}y\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo><mo>|</mo>}x\rangle \left[\alpha e^{i{k}_{z}z}+\beta e^{-i{k}_{z}z}\right]+\mathrm{<mo>|</mo>}-x\rangle \left[\alpha e^{i{k}_{z}z}-\beta e^{-i{k}_{z}z}\right]\mathrm{<mo\; stretchy="false">)</mo>.}$                                 (16)

So after horizontal separation one observes interference pattern along $z$ -axis in both parts, and these patterns are shifted by some phase. The total probability to find the final polarization (post selected is also redundant terminology) $\mathrm{<mo>|</mo>}\pm x\rangle$ is

$P\mathrm{<mo\; stretchy="false">(</mo><mo>|</mo>}{\psi }_{\text{i}n}\rangle \to \mathrm{<mo>|</mo>}\pm x\rangle \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{2}\left[1\pm 2\text{R}e\left(\alpha {\beta }^{\mathrm{<mo>*</mo>}}{e}^{2i{k}_{z}z}\right)\right]\mathrm{.}$                            (17)

There is no problem, if the initial state is $\mathrm{<mo>|</mo>}{\psi }_{\text{i}n}\rangle \mathrm{<mo>=</mo><mo>|</mo>}-x\rangle$ , and the final one is $\mathrm{<mo>|</mo>}{\psi }_{\text{f}}\rangle \mathrm{<mo>=</mo><mo>|</mo>}+x\rangle$ . Probability distribution is well definite. Of course, the distribution (17) is to be averaged over initial distribution of wave vectors. The experimental results can be fitted in the usual way to extract the parameter $al$ , and no “weak value” is needed.

An interesting physics problem with slightly split neutron beam

The discussed above the Stern-Gerlach experiment aimed at measurement the small parameter $al$ is not interesting. The more interesting is the following physical problem. If a single neutron is described by a wave packet (WP), say of de Broglie’s type, then after splitting in a magnetic field it is represented by a superposition of two WPs.¹³ The separation in the field is coherent, so the separated particle is the single one, but its parts propagate at an angle with the same speed, as shown in Figure 1.

The separated parts of the single neutron do overlap some time till they are separated to such a large distance, where they do not overlap anymore, so the single neutron should choose in which part finally to reside. Overlapping wave packets have common polarization rotating in the plane perpendicular to their quantization axis. When transmitted through an analyzer they produce intensity, shown in Figure 2, which depends on position of the analyzer. The decrease of oscillation contrast characterizes the WP size.

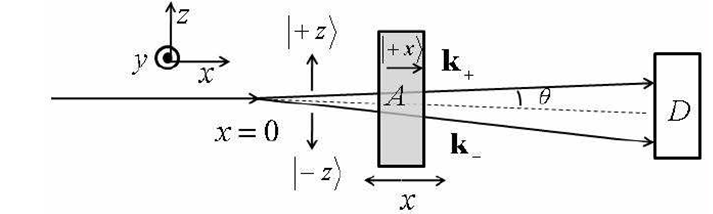
Figure 2 A neutron because of some coherent process splits into two oppositely polarized components, which move with the same speed, but at small angle $\theta \mathrm{<mo>=</mo>}al\mathrm{<mo>/</mo>}{k}^2$ to each other. Superposition of the two components passes through an analyzer, which transmits only neutrons polarized along $x$ -axis. The intensity registered by a detector will oscillate, as is shown in above figure, when the analyzer shifts along $x$ -axis.

If the WP of the neutron is represented by the normalized singular de Broglie’s WP

${\Psi }_{\text{d}B}\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{,}k\mathrm{,}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\sqrt{\frac{q}{2\pi }}\exp \mathrm{<mo\; stretchy="false">(</mo>}ikr-i\omega t\mathrm{<mo\; stretchy="false">)</mo>}\frac{\exp \mathrm{<mo\; stretchy="false">(</mo>}-q\mathrm{<mo>|</mo>}r-kt\mathrm{<mo>|</mo><mo\; stretchy="false">)</mo>}}{\mathrm{<mo>|</mo>}r-kt\mathrm{<mo>|</mo>}}\mathrm{,}$                          (18)

Where $\mathrm{1<mo>/</mo>}q$ is the WP size and $\omega \mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}{k}^2-q^2\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>2}$ , then oscillation is represented by the function

$f\mathrm{<mo\; stretchy="false">(</mo>}X\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>2}\eta {\displaystyle \underset{0}{\overset{1}{\int }}ds\cos \mathrm{<mo\; stretchy="false">(</mo>}sX\mathrm{<mo\; stretchy="false">)</mo>}\frac{\exp \left(-X\sqrt{1-s^2+{\eta }^2}\right)}{\sqrt{1-s^2+{\eta }^2}}\mathrm{,}}$                                      (19)

Shown in Figure 3, where $X\mathrm{<mo>=</mo>2}kx{\theta }^2$ , and $\eta \mathrm{<mo>=</mo>}q\mathrm{<mo>/</mo>}k\theta$ .

Figure 3 Results of numerical calculation according to (19) for $\eta \mathrm{<mo>=</mo>0.1}$ .

Criticism of some papers in the “weak measurements” field

One of the typical papers about”weak measurements”¹⁴ in fact is not related to it, because it uses (8) without “weak value”. In the experiment a laser beam with Gaussian front distribution was transmitted through two polarizers oriented at an angle to each other and registered by a position sensitive detector. To create a small perturbation a thin birefringent plate was placed between two polarizers. In this plate the beam splits into two perpendicularly polarized sub beams slightly shifted in transverse direction by the distance $l$ . One of the beams has gaussian distribution $\exp \mathrm{<mo\; stretchy="false">(</mo>}-x^2\mathrm{<mo\; stretchy="false">)</mo>}$ (for simplicity I put the gaussian width equal to unity), and the second one has distribution $\exp \mathrm{<mo\; stretchy="false">(</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}x-l\mathrm{<mo\; stretchy="false">)</mo>}}^2\mathrm{<mo\; stretchy="false">)</mo>}$ . In the case, when $\alpha \mathrm{<mo>=</mo>}\pi \mathrm{<mo>/</mo>2}$ (remember that “weak measurement” forbids orthogonality of initial and final states), distribution of intensity on the detector is proportional to the function

$F\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\left(e^{-x^2}-e^{{\mathrm{<mo\; stretchy="false">(</mo>}x-l\mathrm{<mo\; stretchy="false">)</mo>}}^2}\right)}^2\mathrm{,}$                                         (20)

 which has two humps (Figure 4) separated by the distance much larger than $l$ . It is erroneously claimed that this large separation of humps is an enhancement of the small separation $l$ . In fact, we see that bad resolution does not permit to notice weak perturbations. There are now a lot of papers published under the banner “weak interaction”. They all are only simulation of research. It is common for all them that there are no problems resolved but only some weak perturbation is included in the experiment and the “weak measurement” is demonstrated by large distribution measured on a detector. There is no other result. Review of all them is a boring and thankless job.

Figure 4 Function $F\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}$ for different $l$ : F1 corresponds to $l\mathrm{<mo>=</mo>0.1}$ , F2 – to $l\mathrm{<mo>=</mo>0.01}$ and F3 – to $l-0.001$ . It is seen that the value of the function decreases with $l$ , but the distance between humps is almost independent on $l$ . Therefore the value of $l$ can be found only by fitting of the experimental data, and the large separation of the humps is not the result of the weak value enhancement.

History of attempts to publish this paper

First I submitted the paper in the Russian journal Uspekhi. It was immediately rejected by Rubakov VA because “the paper contains discussion with another one not published in Uspekhi, and it is not in appropriate form for publication.” The second attempt was Rev. Mod. Phys. It was quickly rejected by Debbie Brodbar Journal Manager Rev. Mod. Phys. Because “it is not suitable for publication in any APS journal.” Next I tried Found. Phys. It was quickly rejected by Fedde Benedictus Managing Editor because “this work is not suitable for publication in Foundations of Physics”.

The science of “weak measurements” is not the only pseudo science. I can mention also EPR paradox, Bell’s inequalities, following from them quantum computing, quantum cryptography, teleportation, and also experimental research related to the Kochen-Specker theorem.

Pseudo EPR paradox

In the "seminal" EPR paper¹⁵ the paradox is formulated as follows: it is possible to predict existence of particles with simultaneously precisely defined momentum and position, but it is forbidden by the uncertainty relations (UR). Therefore the Quantum Mechanics (QM) is not complete. It requires some additional hidden parameters. In fact, resolution of the paradox is trivial. Particles really have precisely defined momentum and position simultaneously, and UR has nothing to do with it. Indeed, the paradox stemmed from incorrect definitions of what are the momentum and position of a particle, and disappears after correction of the definitions. In EPR paper¹⁵ momentum is defined as an eigen value of the momentum operator, i.e. it can exist only in the states, which are eigen vectors of the momentum operator. The only such states are plane waves $\psi \mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}ikx\mathrm{<mo\; stretchy="false">)</mo>}$ . But then, it is impossible to define a probability $w$ to find a particle somewhere. EPR defined it as

$w\mathrm{<mo>=</mo>}{\displaystyle {\int }_a^b}\mathrm{<mo>|</mo>}\psi \mathrm{<mo\; stretchy="false">(</mo>}x{\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}}^{2}dx\mathrm{<mo>=</mo>}b-a\mathrm{,}$                                       (21)

Which is not acceptable, because such a probability is dimensional. The recipe, proposed to students in all the text books on QM, to use plane waves in the form $\psi \mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\exp \mathrm{<mo\; stretchy="false">(</mo>}ikx\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}\sqrt{L}$ with some large scale $L$ , is also unacceptable. Though probability becomes dimensionless $w\mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}b-a\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}L$ , it can be larger than unity, if $b-a\mathrm{<mo>></mo>}L$ . To avoid such cases it is necessary to limit space by impenetrable walls. But then the wave function between the walls is not a plane wave, but $\sin \mathrm{<mo\; stretchy="false">(</mo>}\pi nx\mathrm{<mo>/</mo>}L\mathrm{<mo\; stretchy="false">)</mo>}$ , which is not an eigen function of the momentum operator. We arrive at contradiction, which can be resolved by redefinition of momentum as an expectation value for a given WF representable by a WP. In such a case momentum and position can be defined precisely simultaneously and UR has nothing do not with it. Of course, with such a definition there appear dispersions $\Delta p$ and $\Delta q$ . However for an individual particle they are not statistical uncertainties but characteristics of the WP, which must be studied in experiments. So, in some respect EPR are right that QM is incomplete and requires some new parameters, but they do enrich QM and not make it similar to classical one.

Pseudo EPRB paradox

The EPR paradox related to momentum and position was reformulated by Bohm et al.¹⁶ to polarization of particles. They considered decay of a scalar particle into two spin 1/2 particles and introduced entanglement of the two flying far away particles. According to them, if spin in decay should conserve, then after decay of a scalar particle the state of the daughter particles is described by the common wave function

$\mathrm{<mo>|</mo>}\Psi \rangle \mathrm{<mo>=</mo><mo>|</mo>}\uparrow \rangle \mathrm{<mo>|</mo>}\downarrow \rangle -\mathrm{<mo>|</mo>}\downarrow \rangle \mathrm{<mo>|</mo>}\uparrow \rangle \mathrm{,}$                                              (22)

Where $\mathrm{<mo>|</mo>}\updownarrow \rangle$ denote the states with polarization along any space direction, because the state (22) is invariant with respect to space rotation. However, in their paper the authors contradict to themselves. On one side, discussing the Furry paper,¹⁷ which is in accord with the vision of this my paper, they write:

It is true that in any single case, the total angular momentum will not be conserved (just because the fluctuations of the two particles are now uncorrelated). On the other hand, the uniform probability of all directions will lead to the experimentally observed fact of conservation on the average. But on the other side they write that such vision of QM untenable and require conservation of spin in the decay of a scalar particle into two spinor ones. Violation of angular momentum in individual decay events is evident, for instance, in the decay of a scalar particle into two scalar ones. In an individual event a symmetrical WF of the initial particle is transformed into non symmetrical one after decay. The non symmetrical WF is a superposition of functions with all possible, even and odd, angular moments $L$ . The presence of odd $L$ in such a superposition automatically means violation of space parity. The only limitation in the decay is the requirement that projection of the angular moment on any space direction should be equal to zero. And this requirement is satisfied. But non conservation of angular momentum in an individual event means that there are no ground to believe the spin conservation, and no ground to describe wave function of two particles with the common WF (22).

Pseudo violation of the Bell’s inequalities

It is because of the belief that spin at decay is conserved entanglement of states of far separated particles is accepted for granted and Bell S et al.¹⁸ claimed that the inequalities, which he obtained, are violated in QM. However, if angular momentum in an individual decay is not conserved, then one cannot require conservation of the spin.^19–21 Therefore the particles after decay are not described by the common spinor function (22), but by the integral over angular distribution

$\mathrm{<mo>|</mo>}\Psi \rangle \mathrm{<mo>=</mo>}{\displaystyle \int }\frac{d\Omega }{4\pi }\mathrm{<mo>|</mo>}{\uparrow }_{\Omega }\rangle \mathrm{<mo>|</mo>}{\downarrow }_{\Omega }\rangle \mathrm{,}$                                            (23)

Where $\mathrm{<mo>|</mo>}{\updownarrow }_{\Omega }\rangle$ describe the states of individual particle polarized along the direction $\Omega$ . The probability $d\Omega \mathrm{<mo>/</mo>4}\pi$ is QM probability of transition from initial to a final state. The similar arguments are related to photons going apart after decay.

In absence of entanglements all the Bell’s inequalities are not violated. Let’s look at the Figure 5, which represents scheme of an experiment with photons for demonstration of Bell’s inequality violation. In the experiment the source S emits two photons to Alice and Bob. The photons cross analyzers, the birefringent crystals with axes along vectors $o$ . If the source with probability $d\varphi \mathrm{<mo>/</mo>2}\pi$ around direction of propagation emits two independent photons with parallel polarizations directed at some azimuthal angle $\varphi$ with respect to $o{}_A$ , then electric field of the photon going to Alice is represented as $E\mathrm{<mo>=</mo>}o{}_A\cos \varphi +n{}_A\sin \phi$ . With probability ${{\displaystyle \cos }}^2\varphi$ the photon will be registered by the detector $D^{1A}$ , and with probability ${{\displaystyle \sin }}^2\varphi$ it will be registered by the detector $D^{2A}$ . If axis $o{}_B$ of Bob’s analyzer is turned at an angle $\theta$ with respect to $o{}_A$ , then the going to Bob photon with the same direction of the electric field will be registered with probability ${{\displaystyle \cos }}^2\mathrm{<mo\; stretchy="false">(</mo>}\varphi +\theta \mathrm{<mo\; stretchy="false">)</mo>}$ by the detector $D^{1B}$ and with probability ${{\displaystyle \sin }}^2\mathrm{<mo\; stretchy="false">(</mo>}\varphi +\theta \mathrm{<mo\; stretchy="false">)</mo>}$ it will be registered by the detector $D^{2B}$ .

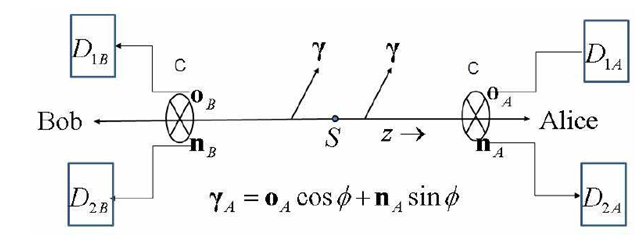
Figure 5  An experiment to demonstrate the EPR paradox in nonlocal quantum mechanics. S-the source of photon pairs with parallel polarization $\gamma$ , flying in two opposite directions to the experimenter Alice and Bob. C-birefringent crystals, analyzing polarization . The crystals have an anisotropy axis $o$ . Photons polarized along $o$ , are registered by the detector $D_1$ , and photons polarized along perpendicular vector $n$ , are recorded by the detector $D_2$ . Photons of the decay have parallel polarizations along vector $\gamma {}_A$ , where $\varphi$ is the azimuthal angle of the polarization vector $\gamma$ with respect to $o{}_A$ .

The goal of the experiment is to measure the correlation

$E\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo>=</mo>}{\theta }_b-{\theta }_a\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{N_{11}+N_{22}-N_{12}-N_{21}}{N_{11}+N_{22}+N_{12}+N_{21}}\mathrm{,}$                               (24)

Where $N_{ij}$ is coincident count rate of detectors $D^{{}_{jA}}$ and $D^{{}_{iB}}$ . In the case of independent photons the averaged over $d\varphi$ correlation is equal^20,21

$E\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>2}\theta \mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>2}\le \mathrm{0.5.}$                                        (25)

However majority of physicists²² believes that the source S emits not photons but a Bell’s entangled wave function

$\mathrm{<mo>|</mo>}\Psi \rangle \mathrm{<mo>=</mo><mo>|</mo>}x\rangle \mathrm{<mo>|</mo>}x\rangle +\mathrm{<mo>|</mo>}y\rangle \mathrm{<mo>|</mo>}y\rangle \mathrm{,}$                          (26)

Where $x$ and $y$ are two arbitrary orthogonal vectors. In such a case the particles going to Alice and Bob become photons only after measurements. The correlation in that case becomes

$E\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>2}\theta \mathrm{<mo\; stretchy="false">)</mo>.}$                                      (27)

Inequality, which is investigated, is a combination of four correlations (24). First ${\theta }_a$ is put to zero and correlation is measured at ${\theta }_b\mathrm{<mo>=</mo>}\pm \pi \mathrm{<mo>/</mo>8}$ . Then analyzer of Alice is turned to ${\theta }_a\mathrm{<mo>=</mo>}-\pi \mathrm{<mo>/</mo>4}$ and measurements at ${\theta }_b\mathrm{<mo>=</mo>}\pm \pi \mathrm{<mo>/</mo>8}$ are repeated. For local theories one should expect

$S\mathrm{<mo>=</mo>}E\mathrm{<mo\; stretchy="false">(</mo>}\pi \mathrm{<mo>/</mo>8<mo\; stretchy="false">)</mo>}+E\mathrm{<mo\; stretchy="false">(</mo>}-\pi \mathrm{<mo>/</mo>8<mo\; stretchy="false">)</mo>}-E\mathrm{<mo\; stretchy="false">(</mo>}\pi \mathrm{<mo>/</mo>4}+\pi \mathrm{<mo>/</mo>8<mo\; stretchy="false">)</mo>}+E\mathrm{<mo\; stretchy="false">(</mo>}\pi \mathrm{<mo>/</mo>4}-\pi \mathrm{<mo>/</mo>8<mo\; stretchy="false">)</mo><mo><</mo>2,}$                                         (28)

Which is satisfied for (25). However for (27) it is violated, because $S\mathrm{<mo>=</mo>2}\sqrt{2}\mathrm{<mo>></mo>2}$ .

It is funny that Bell’s inequalities are formulated for four measurements, whereas it is possible to check them in a single one. If it is impossible to discriminate two correlations (25) and (27) in a single measurement, how then reliable can be a result of four measurements?

In fact it is easy to falsify violation of Bell’s inequalities. It is sufficient to look at (24). To determine count rate $N_{ij}$ it is necessary to subtract a background from the measured countrate. Subtraction of sufficiently large background decreases denominator and increases the correlation as much as you like. For instance, in the paper²³ it is said that the denominator in (24) is equal to 80 per sec. But in determination of $N_{ij}$ the accident coincidence rate equal to 10/sec was subtracted. If not to subtract this value, then denominator will be 120/sec and the reported value S=2.7 will decrease to S=1.8, and there will be no violation of the Bell’s inequality (28). Nobody yet proved that entanglement of separated particles exists. To prove it, it is necessary to shift Alice closer to the source and to use a source with rare controllable photon pairs. If one chooses only those pairs that are detected by $D^{{}_{1A}}$ and at $\theta \mathrm{<mo>=</mo>0}$ looks how many of the photons of these pairs are detected by $D^{{}_{2B}}$ , then one easily concludes: if this number is zero, then entanglement is proven without doubts and inequalities.^24,25

However instead of real research people prefer simulations. A bright example is the recently published two articles,^26,27 where the number of authors become larger than number of players in two football teams. It looks like publication of the similar results by two competing groups. However the fact of simultaneous publication is a demonstration that there is no competition but an agreement to publish simultaneously for not to question priority. The both papers claim loophole free test of Bell’s inequalities (or realism) though the sources in their their experiments emit only partly entangled particles, and they do not consider, what is the fate of the not entangled ones.

Shocking publication on photons entanglement in downconversion²⁵

The above criticism of entanglement of particles outgoing after decay, seems to be invalid, when one considers downconversion²⁵ in a nonlinear BBO crystal of ultraviolet photons with energy E into two photons with energies E/2, as is shown in Figure 6. Since the crystal can create photons with only horizontal, (H), and vertical, (V), polarizations, one can expect that with probabilities 1/2 two photons have individual polarizations HV or VH. To check this suggestion one can look for coincidence counts, when Alice arranges her analyzer to register only V or H photons, then Bob, rotating his analyzer, will see the coincident count rate proportional to ${{\displaystyle \sin }}^2\theta$ , where $\theta$ is the angle between axes of his and Alice’s analyzers. In this model of independent photons with orthogonal polarizations, if Alice arranges her analyzer at angle $\pi \mathrm{<mo>/</mo>4}$ with respect to the vertical direction, then coincidence count rate will not depend on angle $\theta$ of Bob’s analyzer.

Figure 6 Downconversion of photons in a nonlinear BBO crystal. If anisotropy axis lies in the vertical plane, as is shown, the two beams, going to Alice and Bob, with probability 1/2 have polarizations $H_A\mathrm{,}{V}_B$ or $V_A\mathrm{,}{H}_B$ . However, according to,²⁸ the two beams have an entangled state.

However in²⁸ it is declared that the two photons can be prepared in one of the four Bell entangled ${\psi }^{\pm }\mathrm{<mo>=</mo>}HV\pm VH$ or ${\varphi }^{\pm }\mathrm{<mo>=</mo>}HH\pm VV$ states. As a proof of it is demonstration of violation of the Bell’s inequality in all the four Bell states. But a careful examination creates a suspicion that experiment was not done, but only composed with results expected by the authoritative community.

Indeed, on the third page of this paper there is a table, which is represented here (Table 1) by first 3 columns. The S-value is calculated according to (29)

$S\mathrm{<mo>=</mo>}E\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}+E\mathrm{<mo\; stretchy="false">(</mo>}{{\theta }^{\prime }}_1\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}+E\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{{\theta }^{\prime }}_2\mathrm{<mo\; stretchy="false">)</mo>}-E\mathrm{<mo\; stretchy="false">(</mo>}{{\theta }^{\prime }}_1\mathrm{,}{{\theta }^{\prime }}_2\mathrm{<mo\; stretchy="false">)</mo>,}$                      (29)

 Where

$E\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}+C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1^{\perp }\mathrm{,}{\theta }_2^{\perp }\mathrm{<mo\; stretchy="false">)</mo>}-C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1^{\perp }\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}-C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2^{\perp }\mathrm{<mo\; stretchy="false">)</mo>}}{C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}+C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1^{\perp }\mathrm{,}{\theta }_2^{\perp }\mathrm{<mo\; stretchy="false">)</mo>}+C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1^{\perp }\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}+C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2^{\perp }\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}$                    (30)

${\theta }_1\mathrm{<mo>=</mo>}-\pi \mathrm{<mo>/</mo>8}$ , ${{\theta }^{\prime }}_1\mathrm{<mo>=</mo>}+\pi \mathrm{<mo>/</mo>8}$ , ${\theta }_2\mathrm{<mo>=</mo>}-\pi \mathrm{<mo>/</mo>4}$ , ${{\theta }^{\prime }}_2\mathrm{<mo>=</mo>0}$ and ${\theta }^{\perp }\mathrm{<mo>=</mo>}\theta +\pi \mathrm{<mo>/</mo>2}$ , and $C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}$ are coincidence countrate.

Direct calculations of S according to (29)-(30) with given parameters leads to values shown in the fourth column. They do not coincide with measured values, presented in the 3-rd column, therefore there is a contradiction, and no proof of the entanglement. This contradiction is not resolved in the next article.²⁹

It is necessary to point out that, if the photons emitted in the down conversion process are independent, then coincidence count rate is proportional to

$C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1\mathrm{,}{\theta }_2\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{4}\mathrm{<mo\; stretchy="false">[</mo>}{{\displaystyle \sin }}^2\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1+{\theta }_2\mathrm{<mo\; stretchy="false">)</mo>}+{{\displaystyle \sin }}^2\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_1-{\theta }_2\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>,}$                            (31)

And again the calculated quantity S in (29) is also zero.

To compare with down conversion experiments it would be worth to perform the similar experiment with a single photon split coherently in a birefringent prism.³⁰

Impossibility of discussion in present days physics

I submitted a comment about²⁸ to Phys. Rev. Lett. On March 27. After their acknowledgement, I replied. “Dear editors, thank you for the information, I hope you will consider my submission seriously. I tried to send my doubts to the authors, but received no response. I think they have nothing to reject my criticism.” However on March 28 I received the rejection. “We note the paper is more than two decades old and has received much notice - well over 1000 citations. Errors in the paper, if any, have apparently not been significant. Furthermore your Comment is not collegial. It questions the scientific integrity of the authors. This is not acceptable. Accordingly we return the matter to your hands. Yours sincerely, George Basbas Consulting Editor”

My reply was: “Dear George, this paper is fraud. Therefore all the papers based on it are also fraud. I can improve my comment to make it more collegial, if you propose me some changes. I tried to contact the authors; they replied me nothing, because they have nothing to answer my doubts. I understand that you must defend your Esprit de corps. May I ask you, nevertheless, to send them my comment and ask them to reply it even without publication? They will not ignore you. And you will send me their reply, for me to be ashamed to suspect them in fraud. May I hope to continue our correspondence? With respect and understanding, V.Ignatovich” After some correspondence I corrected my comment and made it more collegial. On April 5 I received the letter from George Basbas: “The use of this two-decade old source of entangled photons is ubiquitous, as the current count of over 1400 citing articles illustrates. This in itself is a kind of proof of the correctness of the Letter you criticize. In principle, you can appeal but I see no basis for doing so.”

My reply: “I am grateful for your criticism, it helps me very much. I hope that the new version will satisfy you, but I am ready to improve it even more, if you find it is necessary.”

On May 27 I received: “The complete file concerning the above manuscript has been reviewed by a Divisional Associate Editor. The appended comments advise against publication in Physical Review Letters. The Editors accept this advice. Your appeal has been considered, and our decision to reject is maintained. George Basbas Consulting Editor” The letter contained the decision of Jian-Wei Pan Divisional

Associate Editor:

“The technique of spontaneous parametric down-conversion and the particular setup by P. Kwiat PRL 1995 has been widely used in almost all the laboratories on optical quantum information processing worldwide. This manuscript should be rejected completely.”

My reply: “Dear George, tell me, please, whether Kwiat replied to my comment? Or you did not send it to him? If yes, why? I myself is amused how it can happen. I am sure that the similar installations can be used, but all the Bell’s inequalities can be falsified by subtracting too much background. Can you imagine, if someone submit to you a paper, in which honestly shown that the Bell’s inequality is not violated. I am sure you will reject it as erroneous, because there are million experiments, which have shown the opposite. Entanglement can be checked without inequality, but why to do that, if you will reject any paper, which will doubt it? You know, I was expelled from arXiv, when started to criticize EPR paradox. If you publish my comment, people will be braver. My comment is not erroneous, you can calculate yourself. Rejecting my comment you suppress any discussion in science and therefore resist its development. Tell me, please, whether I am not right. Situation in science is horrible. Hope to get your reply.”

And George Basbas replied: “Kwiat et al.,²⁹ state in their letter that $S<=2$ for any local realistic theory. They do not calculate S. You do and get a result that satisfies the inequality. They measure S and get a result that violates the inequality. This is the way nature is, not an error. We found no justification for consulting Kwiat about this. Your persistence in the matter led us to consult an editorial board member (Divisional Associate Editor). The DAE confirms our decision not to consider the paper further. This email necessarily ends our communications on your Comment. We have to move on.”

I was shocked: “Dear George, I see from this your letter, that you do not understand well the situation. I would like to explain it to you, if you agree to continue our correspondence. However, if you will understand, you will be ashamed, and at the same time you will not be able to change your decision, because it will be dangerous for your career. So, do you want to continue?” He did not.

Laboratory work for students

In^24,25 a scheme of an experiment was proposed for obtaining an entangled photon pairs. It uses two beta barium borate crystals of 0.1mm thickness with an anisotropy axis directed at an angle of ${29}^0$ to the normal to the largest crystal face. In the first crystal, the plane of the anisotropy axis and the normal to interface is vertical, and a laser beam with horizontal linear polarization (an ordinary ray in the crystal) passes through the crystal freely, but a photon with vertical polarization (extraordinary) splits into two ordinary horizontally polarized photons, as shown in Figure 7.

Figure 7 In each crystal an extraordinary beam splits into 2 ordinary rays. Due to the fact that the refractive index of an extraordinary ray is less than the ordinary, the born photons propagate along the generatrix of the cone with an angle at the vertex determined by the law of conservation of the momentum.

In the second crystal, rotated by ${90}^0$ with respect to the first one, a horizontally polarized photon is split into 2 vertically polarized photons. The incident laser beam is polarized at an angle $\theta$ to the vertical. It is asserted that along the two opposite generatrices of the cone, an entangled state of the type

$\mathrm{<mo>|</mo>}{H}_A\mathrm{,}{H}_B\rangle \cos \theta +e^{i\varphi }\mathrm{<mo>|</mo>}{V}_A\mathrm{,}{V}_B\rangle \sin \theta \mathrm{.}$        (32)

Is generated. In this case, the entangled state of two photons is imperceptibly replaced by entanglement of two pairs of photons. In fact, the two pairs are in no way related to each other, because they arise from different laser photons. With probability ${{\displaystyle \cos }}^2\theta$ one pair of photons with individual horizontal polarizations is generated, and with probability ${{\displaystyle \sin }}^2\theta$ another pair of photons with individual vertical polarizations is generated. Moreover, if the first pair generated in the first crystal consists of photons at the top and bottom points of the emission cone, then in the second crystal the generated pair of photons only with small probability $\Delta \varphi \mathrm{<mo>/</mo>2}\pi$ will be at the same points, where $\Delta \varphi$ is the resolution angle of the installation. Therefore, it is wrong to consider pairs of photons with horizontal and vertical polarizations as related to one laser photon. The VF of photons is the mixed one, i.e. with probability ${{\displaystyle \cos }}^2\theta$ photons are polarized horizontally, and with probability ${{\displaystyle \sin }}^2\theta$ they are polarized vertically. One can even not discuss the phase $\varphi \mathrm{<mo>=</mo>2}\pi d\mathrm{<mo>/</mo>}\lambda$ in (32), where $\lambda$ is the wavelength of the incident photon, and d is the distance between the splitting points of split photons in the two crystals. The phase uncertainty at $\lambda \mathrm{<mo>=</mo>405}$ nm and the crystal thickness of 0.1mm is very high, and it cannot be compensated by any optical device. This proves once again that the two terms are in no way connected with each other. If the analyzers of Alice and Bob are rotated to angles ${\theta }_A$ and ${\theta }_B$ , respectively, then the probability of registration in coincidence by a single detector at each of them is

$C\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{,}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{{\displaystyle \cos }}^2\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}{{\displaystyle \cos }}^2\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}{{\displaystyle \cos }}^2\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}+{{\displaystyle \sin }}^2\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}{{\displaystyle \sin }}^2\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}{{\displaystyle \sin }}^2\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>.}$         (33)

Suppose, however, that the entanglement does really exist and then the count rate in coincidence will be

$P_{AB}\mathrm{<mo>=</mo>}\langle \mathrm{<mo>|</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}+e^{i\varphi }\sin \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}\sin \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}\sin \mathrm{<mo\; stretchy="false">(</mo>}\theta {\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}}^2\rangle \mathrm{<mo>=</mo>}$   
$\mathrm{<mo>|</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}\theta {\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}}^2+\mathrm{<mo>|</mo>}\sin \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}\sin \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}\sin \mathrm{<mo\; stretchy="false">(</mo>}\theta {\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}}^2\mathrm{,}$                 (34)

Where the angle brackets mean averaging over the phase. The obtained result proves (7); which testifies in favor of locality. However, the authors of²⁴ fixed the phase at will and, used the expression

$N\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{,}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}A\mathrm{<mo>|</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}\cos \mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}+e^{i\varphi }\sin \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_A\mathrm{<mo\; stretchy="false">)</mo>}\sin \mathrm{<mo\; stretchy="false">(</mo>}{\theta }_B\mathrm{<mo\; stretchy="false">)</mo>}\sin \mathrm{<mo\; stretchy="false">(</mo>}\theta {\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo>}}^2+C$              (35)

With unknown parameters $A$ , $\varphi$ , $\theta$ and C. The value ${\chi }^2$ that only characterizes the quality of the fit, they do not report. It is necessary to note that the countrate of single pulses in this work is 100 times higher than the countrate in coincidences. Therefore, there is no confidence in these results.

Massive attack on locality

In 2015, two publications^26,27 appeared in one issue of Phys. Rev. Lett, in which the number of co-authors exceeds the number of 2-3 football teams. A simple analysis of the works shows that they are not related to the announced problem, and a large number of co-authors testify to the desire, with the help of masshood, to give them a "greater credibility." In both works, the entanglement of two photons is replaced by the artificially devised²⁴ entanglement of two pairs of photons, which has nothing to do with the problem originally formulated in the EPRB. In the first paper two pairs of photons are created in the same ppktp crystal as shown in Figures 8 (A & B) when laser photons with orthogonal polarization traverse it in opposite directions, and in the second paper the laser photons with orthogonal polarizations traverse the same ppktp crystal at two separate points. In both works partially entangled states are considered. If such states were possible, it would mean that with some probability quantum mechanics is local, and with another probability it is nonlocal. It means an introduction of a new parameter, which, according to EPR, makes quantum mechanics more complete, though does not resolve the paradox.

Figure 8 The scheme for obtaining entangled states of two pairs of photons. The incident laser photon is linearly polarized at angle $\theta$ with respect to vertical axis. In the left panel²⁶ vertically and horizontally polarized parts of the incident photon traverse the nonlinear ppktp crystal in different directions. In the right panel²⁷ vertically and horizontally polarized parts of the incident photon traverse the nonlinear ppktp crystal at two different points. The two photons are sent to Alice and Bob, who have analyzers and one detector each. HWP stands for a half-wave plate, and DM for a dichromatic mirror. Many optical elements are omitted.

Pseudo bell states

Last years it became usual to generalize the notion of the Bell state by adding position or momentum degrees of freedom to polarization ones. Typical example is the work³¹ where in the Si neutron interferometer a neutron after splitting in the first crystal and polarization in two paths is represented by the wave function

$\mathrm{<mo>|</mo>}\Psi \rangle \mathrm{<mo>=</mo>}\frac{1}{\sqrt{2}}\left(\mathrm{<mo>|</mo>}+x\rangle \mathrm{<mo>|</mo>}I\rangle \pm \mathrm{<mo>|</mo>}-x\rangle \mathrm{<mo>|</mo>}II\rangle \right)\mathrm{,}$           (36)

Where $\mathrm{<mo>|</mo>}\pm x\rangle$ denote neutron polarization states along or against $x$ -axis, and $\mathrm{<mo>|</mo>}I\mathrm{,}II\rangle$ denote positions of the neutron along the two paths after splitting. The state (36) is not an entangled one. It is a superposition of states of a single neutron, but it looks like (22), and because of that it was called an entangled state with different degrees of freedom. There was even devised a Bell’s inequality dependent on two phases: $\alpha$ , related to spin degree, and $\chi$ , related to path degree. And for some combination of these phases it was found that the value of $S$ , similar to (29), is larger than 2, which proves entanglement of two degrees of freedom. It is evident that such works are not research in the field of fundamental physics, but only a simulation of it.

Since entanglement of separated particles has not been proven yet, all the sciences with manipulation of entangled particles, like quantum computers, quantum cryptography and teleportation, are only the pseudo ones. They permit manipulations with symbols on a paper and will never bring a result, which can be physically realizable.

Quantum cryptography

There are mainly two protocols of creation of a secret key with the help of quantum mechanics. One is so called BB [84] protocol is without entangled particles,³² and the other one³³ with them. In the first one Alice sends to Bob photons with, say, randomly linear or circular polarizations. And Bob randomly measures them with linear or circular analyzers. They should tagg these photons for not to miss a single one. After sending a sequence, Alice connects to Bob via public phone and asks him which analyzer he used for every photon. They discard those photons, for which Bob did not guess correctly the analyzer, and remaining photons (suppose there was no eavesdropping) will produce a key number composed of 0 and 1. For instance, in the case of linear polarization horizontal one means 1, and vertical one means 0. In the case of circular polarization the left one means 1, and the right one means 0. It is not explained how do Alice and Bob secretely exchange the convention which polarization is zero, and which one is 1. There are some publications about experiments in literature. One of them³⁴ reports quantum key distribution via BB⁸⁴ protocol over distance 144km on Canary islands via a low earth satellite. In the experiment mainly technical problems with multi photon pulses are discussed, and, of course, in conclusion it was said “The current outdoor experiment definitely shows the feasibility of secure key exchange with low-earth-orbit satellites.”

Pseudo quantum cryptography

In the case of use of entangled states Alice and Bob accumulate in their refrigerators (to avoid decoherence) a lot of labelled entangled pairs, and at fixed time Alice starts to measure her photon, immediately preparing polarization of the Bob’s companion. Bob measures his photon with his analyzer, and again after some measurements calls to Alice to report which analyzer he used for every pair. Of course, for the sake of economy of entangled particles Alice should tell to Bob by public phone, which type of measurement she will do, for Bob should know exactly what he must do. Such communication will not help to eavesdroppers, because they will not know the results of measurements. But Alice and Bob beforehand should make somehow a secret convention, which result to get as 0 and 1. This method was not yet checked experimentally because there is still no in the world a company, which can produce enough number of high quality entangled pairs successfully resisting all the decoherences in our noisy environment.

Pseudo quantum teleportation

The teleportation means that Alice wants to send an unknown to her photon state $\alpha \mathrm{<mo>|</mo>0}\rangle +\beta \mathrm{<mo>|</mo>1}\rangle$ to Bob. To do that Alice and Bob should have in their disposal an entangled photon pair $\mathrm{<mo>|</mo>0}\rangle \mathrm{<mo>|</mo>0}\rangle +\mathrm{<mo>|</mo>1}\rangle \mathrm{<mo>|</mo>1}\rangle$ . For teleportation Alice manipulates with her photon common with Bob and the unknown photon. As a result the three photons become in the state³⁵

$\mathrm{<mo>|</mo>0}\rangle \mathrm{<mo>|</mo>0}\rangle \mathrm{<mo\; stretchy="false">(</mo>}\alpha \mathrm{<mo>|</mo>0}\rangle +\beta \mathrm{<mo>|</mo>1}\rangle \mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{<mo>|</mo>1}\rangle \mathrm{<mo>|</mo>0}\rangle \mathrm{<mo\; stretchy="false">(</mo>}\alpha \mathrm{<mo>|</mo>0}\rangle -\beta \mathrm{<mo>|</mo>1}\rangle \mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{<mo>|</mo>0}\rangle \mathrm{<mo>|</mo>1}\rangle \mathrm{<mo\; stretchy="false">(</mo>}\alpha \mathrm{<mo>|</mo>1}\rangle +\beta \mathrm{<mo>|</mo>0}\rangle \mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{<mo>|</mo>1}\rangle \mathrm{<mo>|</mo>1}\rangle \mathrm{<mo\; stretchy="false">(</mo>}\alpha \mathrm{<mo>|</mo>1}\rangle -\beta \mathrm{<mo>|</mo>0}\rangle \mathrm{<mo\; stretchy="false">)</mo>.}$ (37)

After that Alice measures her two photons and informs Bob about the result. If she finds the result $\mathrm{<mo>|</mo>00}\rangle$ , Bob knows that he has just that unknown photon, which Alice wanted to teleport to him. If her measurement is, say $\mathrm{<mo>|</mo>10}\rangle$ , then Bob should change a phase of his photon to get the teleported one, and so on.

It is necessary to mention that in literature there are publications on experimental teleportation. However there are no experiments with manipulation of three photons as was discussed above. In³⁶ only two photons were used, and entanglement of polarizations was replaced by entanglement with different degree of freedom, like path or momentum. So it is not a real teleportation, but a simulation of it.

A vanity around kochen-specker theorem

In the literature one can find a lot of discussion of the Kochen-Specker theorem. Even full conferences are arranged in its honor. It is a sophisticated intellectual exercise, which is practically useless. It proves that QM cannot be reduced to classical one, like wave mechanics cannot be reduced to simple mechanics, which is evident, and experiments like^31,37,38 and equilibristic with terminology like contextuality and non-contextuality are only a simulation of activity in the fundamental physics research. The essence of the theorem is: if we have commuting operators $A$ , $B$ and $C\mathrm{<mo>=</mo>}AB$ , all having eigenvalue -1, then we cannot ascribe to $A$ and $B$  noncontextual, i.e. classical, values $v\mathrm{<mo\; stretchy="false">(</mo>}A\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}B\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-1$  such that $v\mathrm{<mo\; stretchy="false">(</mo>}C\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}A\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}B\mathrm{<mo\; stretchy="false">)</mo>}$ . And experimenters proved it. They measured an averaged value $\langle S\mathrm{<mo>=</mo>1}-A-B-C\rangle$ , which in classical case should be less than 2, and in the case of quantum mechanics should be less than 4. They were proud to get $\langle S\rangle \mathrm{<mo>=</mo>3.138}\pm \mathrm{0.015<mo>></mo>2}$ , which proves, that quantum mechanics cannot be described in classical terms, which is absolutely evident even without any measurement.

On quantum computers

The theory of quantum computers is very sophisticated and it is impossible to characterize it in few words. But it is a pseudoscience, when it deals with entangled states at different registers. Moreover, the goal of quantum computers is to factorize big numbers with the help of the Shor algorithm. It is necessary to point out that such a factorization was recently achieved in an optical experiment.³⁹

One of the ways to factorize a big number is to look at the so called truncated Gauss sum

$f\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{,}N\mathrm{,}M\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{M}{\displaystyle \sum _{m\mathrm{<mo>=</mo>1}}^M}\exp \left(2\pi i{\mathrm{<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo>}}^2\frac{N}{x}\right)\mathrm{.}$            (38)

In fact, it is possible to quickly factorize quite large numbers with a personal computer. On Figure 9 there is shown function $F\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}-f\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{,}N\mathrm{,}M\mathrm{<mo\; stretchy="false">)</mo>}$  for $N\mathrm{<mo>=</mo>1133<mo>*</mo>1153}$  and $M\mathrm{<mo>=</mo>18}$  calculated in several seconds.

Figure  9 Factorization for several seconds on a computer of the number N=1133*1153 with the function $F\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}-f\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{,}N\mathrm{,}M\mathrm{<mo\; stretchy="false">)</mo>}$ where M=18, and $F\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{,}N\mathrm{,}M\mathrm{<mo\; stretchy="false">)</mo>}$ is the truncated Gauss sum.³⁸

A remark on other pseudosciences

In between pseudo sciences I would like to mention also experiments on searching something, which is absent, with higher and higher precision. For instance, present day experiments on neutron electric dipole moment, experiments on neutron life time, and experiments on searching violation of the weak principle of equivalence. They played positive role in science at an initial stage of technology development, but now have lost their actuality.

In fact QM is really incomplete. It contains many contradictions and it requires introduction of new parameters. Here I present a list of 8 real physics problems worth of investigation, and other people can enlarge this list.

Proof of the entanglement

We need not an evidence of entanglement like violation of Bell’s inequality. This evidence can be falsified. We need a direct proof. For that Alice should be closer to the source of the entangled particles. Analyzers of Bob and Alice should be arranged parallel to each other. All the pairs should be tagged and Bob should register only those particles, which correspond to particles registered by the specific Alice’s detector. Then probability of registration by different Bob’s detectors will prove existence or not existence of the entanglement of far separated particles.²¹

To check contradiction of the density matrix in quantum mechanics

In⁴⁰ it is shown that, if a nonpolarized beam is split into two polarized ones, and then polarized beams are united, one gets again nonpolarized beam, which however contains the fixed quantization axis. Direction of this quantization axis can be experimentally measured, though according to quantum mechanics it is impossible. My paper submitted to JETP was rejected. Referee wrote that the paper is evidently erroneous. The problem is only how to find the error, but this is the task for the author.

Contradictions of the quantum scattering theory

QM contains contradictions.⁴¹ First of all description of scattering with spherical functions is not legitimate. Scattering process must describe transition of a free particle to the free ones. Spherical waves contain part, which can be interpreted as a bound state to scattering center. It renormalizes scattering on a crystalline plane to zero,⁴² and therefore forbids diffraction from crystals, which contradicts to observations. It was shown^41–43 that, if one excludes from spherical wave the binding part, one gets a superposition of free particles after scattering. However the new superposition gives only probability of scattering and the problem arises how to find a cross section. It seems that presentation of the wave function with wave packet can help. But an attempt to describe scattering of a WP on a point scatterer⁴³ shows that the cross section in linear theory does not depend on whether WP covers the scatterer or not. It depends only, if the Schrödinger equation contains nonlinear parts, which also requires some new parameters. Moreover, the corrected scattering theory predicts different results, when calculations are made directly in Laboratory reference frame, or after transmission of calculations made in the center of mass reference frame.

My paper about crystalline plane submitted to Am. J. Phys was rejected by a referee, who wrote: "Paradoxes and ": contradictions in present day scattering theory:" arise because of author’s misleading interpretations of some fundamental results of the scattering theory." I am sure he will not be able to point out what fundamental results have misleading interpretation. But an author is not permitted to argue with referees.

Neutron holography without reference beam

It is possible to use spin property of neutrons to produce two waves that interfere with each other after scattering and produce a hologram.⁴⁴ It is also possible to use the visible coherent light to enlighten the hologram and to observe the internal structure, magnetic or not magnetic in visible light. However nobody tried yet to realize such an opportunity.

Experiments on creation of an object similar to the ball lightning

It is well known that internal total reflection of light from an interface between two media usually is accompanied with absorption and decrease of the reflection coefficient. Therefore, if one sends a photon into a spherical glass shell in a mode of whispering gallery, the photon will soon disappear. However, if the glass shell is surrounded by an excited gas with excitement energy matching the photon frequency, then reflection coefficient at every internal reflection is larger than unity,⁴⁵ and electromagnetic energy accumulates during travelling of the photon along the whispering gallery. In milliseconds time energy can reach many Joules, the glass at such energy melts, but liquid glass will not drop down because of electrostriction forces. Nobody tried yet to check this idea.

Investigation of the neutron wave packet properties

New parameters are required in quantum mechanics to describe WP of particles,¹³ its size and form. These parameters can be found experimentally as was discussed above.

 To check non conservation of energy in reflection and transmission of a neutron by a mirror. There are many interesting experiments related to properties of particles and predictions of QM: one of them is related to violation of energy conservation at an individual act of neutron reflection from a foil.^46,47

To consider singular states in hydrogen atom and their relation to cold nuclear synthesis. It is possible to get a new unexpected result in quantum mechanics for even such a completely studied system as a hydrogen atom.^48,49 But all the publications of something new are completely suppressed by those, who consider QM complete, enjoy philosophy of nonlocality, and think that knowledge presented in textbooks is the last holy truth.

None.

Author declares there is no conflict of interest.

1. Aharonov Y, Albert DZ, Vaidman L. How the Result of a Measurement of a Component of the Spin of a Spin-1/2 Particle Can Turn Out to be 100. Physical Review Letters. 1988;60(14):1–4.
2. Leggett AJ. Comment on How the Result of a Measurement of a Component of the Spin of a Spin- z Particle Can Turn Out to be 100. Physical Review Letters. 1989;62(19).
3. Peres A. Quantum Measurements with Postselection. Physical Review Letters. 1989;62(19).
4. Duck M, Stevenson PM, Sudarshan ECG. The sense in which a weak measurement of a spin 1/2 particle’s spin component yields a value 100. Physical Review D. 1989;40:2112–2117.
5. Parrott S. What do quantum weak measurements actually measure? Cornell University Library, USA. 2009.
6. Svensson BEY. Pedagogical Review of Quantum Measurement Theory with an Emphasis on Weak Measurements. Quanta. 2013;2(1):1–33.
7. Tamir B, Cohen E. Introduction to Weak Measurements and Weak Values. Quanta. 2013;2(1):1–11.
8. Dressel J, Malik M, Miatto FM, et al. Colloquium: Understanding Quantum Weak Values: Basics and Applications. Reviews of Modern Physics. 2014;86(1):1–10.
9. Starling DJ, Dixon PB, Jordan AN, et al. Precision frequency measurements with interferometric weak values. Physical Review A. 2010;82(6).
10. Bow E. Are weak values quantum? Don’t bet on it. Perimeter Institute for Theoretical Physics, Canada. 2014.
11. Dixon PB, Starling DJ, Jordan AN, et al. Ultrasensitive Beam Deflection Measurement via InterferometricWeak Value Amplification. Physical Review Letters. 2009;102(17):1–4.
12. Magaáa-Loaiza OS, Mirhosseini M, Rodenburg B, et al. Amplification of Angular Rotations Using Weak Measurements. Physical Review Letters. 2014;112(20).
13. Ignatovich V. Proposal of an Experiment to Investigate Properties of the Neutron Wave-Packet. SCIREA Journal of Physics. 2016;1(1):1–12.
14. Ritchie NWM, Story JG, Hulet RG. Realization of a Measurement of a Weak Value. Physical Review Letters. 1999;66(9).
15. Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Physical Review Journal Archive. 1935;47(10):777–780.
16. Bohm D, Aharonov Y. Discussion of experimental proof for the paradox Einstein, Rosen, and Podolsky. Physical Review Journal Archive. 1957;108(4):1070–1076.
17. Furry WH. Note on the Quantum-Mechanical Theory of Measurement. Physical Review Journal Archive. 1936;49(5).
18. Bell JS. On the Einstein-Podolsky-Rosen paradox. Physics. 1964;1(3):195–200.
19. Bell JS. Speakable and unspeakable in quantum mechanics. Cambridge University press, UK, 2004. p. 1–14.
20. Ignatovich VK. On EPR paradox, Bell’s inequalities and experiments which prove nothing. Concepts of Physics. 2008;5(2):227–278.
21. Ignatovich VK. Closer Look at EPR Paradox and Bell’s Inequality. American Journal of Modern Physics and Application. 2015;2(2):16–20.
22. Ignatovich VK. Single Measurement Bell’s Inequality with Detection Efficiencies. Physics Journal. 2016;2(1):1–5.
23. Mermin ND. Hidden variables and the two theorems of John Bell. Reviews of Modern Physics. 1993;65(3):803–815.
24. Aspect A, Grangier P, Roger G. Experimental Realisation of Einstein-Podolskii-Rosen-Bohm Gedanken experiment: A new violation of Bell’s inequalities. Physical Review Letters. 1982;49(2):1–4.
25. Dehlinger D, Mitchell MW. Entangled photon apparatus for the undergraduate laboratory. American Journal of Physics. 2002;70 (9):898–902.
26. Dehlinger D, Mitchell MW. Entangled photons, nonlocality, and Bell inequalities in undergraduate laboratory. American Journal of Physics. 2002;70(9):903–910.
27. Giustina M, Versteegh MAM, Wengerowsky S, et al. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Physical Review Letters. 2015;115(25):1–7.
28. Shalm LK, Meyer-Scott E, Christensen BG, et al. Strong Loophole-Free Test of Local Realism. Physical Review Letters. 2015;115(25):1–10.
29. Kwiat PG, Mattle K, Weinfurter H, et al. New High-Intensity Source of Polarization-Entangled Photon Pairs. Physical Review Letters. 1995;75(24):1–6.
30. Kwiat PG, Waks E, White AG, et al. Ultrabright Source of Polarization-Entangled Photons. Physical Review A. 1999;60(2).
31. Ignatovich VK, Ignatovich FV. A Proposal for Optical Experiments on Nonlocality with a Linear Anisotropic Crystal. Theoretical Physics. 2016;1(1):14–17.
32. Hasegawaa Y, Loidla R, Badureka G, et al. Violation of Bell-type inequality in single-neutron interferometry: quantum contextuality. Nuclear Instruments and Methods in Physics Research A. 2004;529(1–3):182–186.
33. Bennett CH, Brassard G, Mermin ND. Quantum cryptography without Bell’s theorem. Physical Review Letters. 1992;68(5):557–559.
34. Ekert AK. Quantum Cryptography Based on Bell’s Theorem. Physical Review Letters. 1991;67(6):661–663.
35. Schmitt-Manderbach T, Weier H, Furst M, et al. Experimental Demonstration of Free-Space Decoy-State Quantum Key Distribution over 144 km. Physical Review Letters. 2007;98(1):1–4.
36. Rieffel E, Polak W. An Introduction to Quantum Computing for Non-Physicists. ACM Computing Surveys. 2000;32(3):300–335.
37. Boschi D, Branca S, Martini FD, et al. Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Physical Review Letters. 1998;80:1121–1125.
38. Hasegawa Y, Loidl R, Baron M, et al. Quantum contextuality in neutron interferometer experiments. Physica B: Condensed Matter. 2006;385–386(2):1377–1380.
39. Hasegawa Y, Loidl R, Badurek G, et al. Quantum Contextuality in a Single-Neutron Optical Experiment. Physical Review Letters. 2006;97(23).
40. Tamma V, Zhang H, He X, et al. New factorization algorithm based on a continuous representation of truncated Gauss sums. Journal of Modern Optics. 2009;56:2125–2132.
41. Ignatovich VK. Contradiction of the DENSITY MATRIX Notion in Quantum Mechanics. Universal Journal of Physics and Applications. 2013;1(2):189–195.
42. Ignatovich VK. Contradictions in scattering theory. Old and New Concepts of Physics. 2004;1(1):1–53.
43. Ignatovich VK. Diffraction off a crystalline plane as another example of contradictions in the quantum scattering theory. Proceedings of ISINN. 2013;21:42–54.
44. Ignatovich VK. Apocrypha of Standard Scattering Theory (SST) and Quantum Mechanics of the de Broglie wave packet. Proceedings of ISINN. 2010;9:116–127.
45. Gahler R, Ignatovich VK. Neutron holography without reference beam. Physics Letters A. 2010;362(5–6):393–400.
46. Ignatovich VK, Ignatovich FV. A proposed experiment on ball lightning model. Physics Letters A. 2011;275(40):3537–3540.
47. Ignatovich VK. Change of neutron energy at reflection from and transmission trough a matter layer. SCIREA Journal of Physics. 2013;1(1):41–51.
48. Utsuro M, Ignatovich VK, Geltenbortb P, et al. Experimental test of the de Broglie wave packet nature of the neutron. Proceedings of SPIE. 1999;3767:372–379.
49. Ignatovich VK. Singular Bound States and Cold Nuclear Fusion. Physics Journal. 2016;2(1):6–10.