In this article we have revisited the orbital calculations for a celestial mechanical system using the relativistic Lagrangean formalism. The differential equations obtained through this procedure, involving a perturbative expansion of the relativistic Lagrangean constituted on an effective gravitational potential based on the classical gravitational potential, presented good solutions for planetary orbits at our solar system. The validity of the trajectories obtained was carefully observed for Mercury, interacting only with the sun, a typical two body problem. Its natural precession, predicted by general relativity, can be recovered with the perturbed Lagrangean, and Mercury trajectory seems to be chaotic in the sense of KAM theorem when we analyzed the Poincare Map in planet phase space.

Keywords: relativistic mechanic, euler-lagrange, effective potential, chaotic motion

The measurements studies associated with plan¬etary orbits for our solar system has been casted as main task for many scientists and natural philoso¬phers before Tycho Brahe and Johannes Kepler, but all of them used a geometric description in their works. However, from the XVII century, with the advent of Newtonian mechanical laws and differential and integral calculus, it was established the unification of geometry with the dynamical prescription, now known as celestial mechanics.¹ Nowadays, the the¬ory of special and general relativity are used to de¬scribe with greater precision the planets motion and cosmological entities. Motions that, in generally, given the nonlinear features of the differential equations in¬volved seems to present chaotic behavior.^2–7 The complexity of these systems, become more evident when numerical techniques are used to solve the nonlinear relativistic equations^8,9 that arises for example at studies of galaxies dynamics; universe expansion; orbital precession; besides several other phenomena in different scales. In this article we revisited the Mercury perihe¬lion issue. This problem is widely known and there are some works regarding this subject,^10,11 as observed by Peters¹² in 1987 using only special relativity. In addition we take into account some information"s about the chaotic aspect of the system beyond the use of a Lagrangean formalism with a more simple mathematical approach considering an effective gravitational potential based on the classical gravitational potential, similar to the one proposed by Phipps¹³ inspire that for simplicity we consid-ered that the system center of mass is coincident with the sun position.. In order to achieve this, our article is organized as: a brief overview on the Newtonian (non relativistic) problem, later we deal with the rela¬tivistic Lagrangean formulation of the problem, pre¬senting the perturbative Lagrangean obtained and the correspondent motion equations that were numeri¬cally solved and discussed from the chaotic point of view.

Newtonian and relativistic lagrangean formal­ism

The Newtonian model for objects under the ac­tion of a central potential has been known for cen­turies and can be found in appropriate literature^14,15 The fundamental equation that is used in order to obtain orbits, and also for solving countless other problems in physics, is Newton’s, well-known, second law${\displaystyle \sum \overrightarrow{F}=d\overrightarrow{p}/dt.}$

The solution of this equation under the influence of the gravitational potential gives us the equation for $\text{r(}\theta \text{)}$ (using polar coordinates with the sun or the most massive object at the center of the reference frame) and, consequently, Kepler’s 1st Law, the orbits law. We can note this by observing that the equation of $\text{r(}\theta \text{)}$ , which follows below and is a solution for the newtonian motion equation in this case, is an ellipse equation

$r\left(\theta \right)=\frac{\frac{L^2}{GM{m}^2}}{1+Acos\left(\theta -{\theta }_0\right)},$

Where$A,e,\theta$ are integration constants, L is the object (planet) conserved total angular momentum, G is the gravitational constant, M is most massive object mass, and m is the other(smaller) mass. This solution depends only on system constants, but we can write them from the elliptical geometrical parameters, as well as, eccentricity, semi major-axis and semi minor-axis. Thus, applying NASA website planetary data of our solar system¹⁶ on equation (1) and adjusting the respective parameters, the graphic in Figure 1 is obtained.

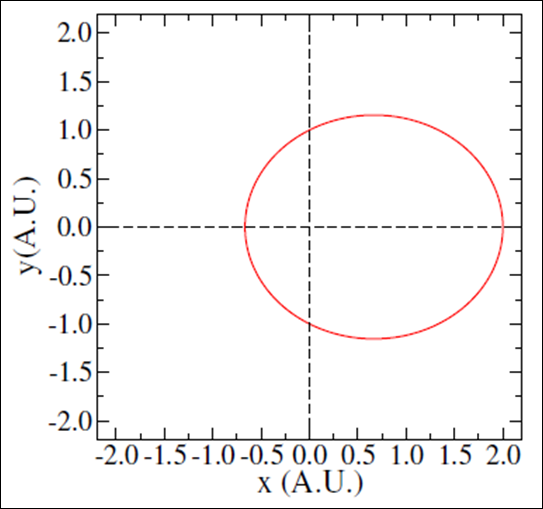
Figure 1 A typical elliptical planet orbit, for the case $\frac{L^2}{GM{m}^2}=1.0$ and A = 0.5.

Einstein’s Special Relativity (SR), established since 1905, shows that the orbits of the planets, which are very close to highly massive objects, as our sun, cannot be described as perfect ellipses.

The success of the SR is detected by its application in various fields of modern technology, such as in telecommunications, mobile devices, supercomputers, the Internet, even in the great theories of elementary particles, currently tested in the LHC-CERN. Einstein established that the velocity of light in the vacuum$\text{c = 299}\text{.792}\text{.458m/s,}$  is a limiting speed of the universe, and nothing could travel with a velocity higher than it, and no massive bodies can be accelerated to this value. In order to carry out this information the Lorentz transformations of coordinates must be used. At that configuration, the Lorentz factor,^17,18 plays an important role.

We have considered a conservative system where the relativistic Lagrangean associated with the classical Newtonian potential is written as

$\mathcal{L}=-m{c}^2{\left[1-\frac{v^2}{c^2}\right]}^{1/2}+\frac{GMm}{r}. \left(1\right)$

Here v is the module of its velocity. Here again the most massive object is at rest, positioned at the system center of mass, and the other orbits around it. The proposed lagrangean implies on a correction to the original classical Lagrangean in similar terms to the one developed in perturbation theory.^19,20

This type of derivation was previously performed in details by Lemmon²¹ and D’Elisio²² separately. Considering the following change of variables

$\frac{\gamma }{R_0}=x, \frac{\dot{r}}{R_0}=\dot{x}, \frac{\mathcal{L}}{m{c}^2}=\stackrel{}{\tilde{\mathcal{L}}}, \alpha =\frac{GM}{R_0{c}^2}, \tau =\frac{R_0}{c}$

Converting the original Lagrangean into

$\stackrel{}{\tilde{\mathcal{L}}}=-{\left[1-{\tau }^2\left({\dot{x}}^2+x^2{\dot{\theta }}^2\right)\right]}^{1/2}+\alpha \frac{1}{x} \left(2\right)$

Here, we assume that $R_0=1A.U.$ (Astronomical Unity-A.U.), hence the equation (2) is partially dimensionless since $\tau$ is the necessary time to the light to cover 1A.U.

The normalized Lagrangean with respect to the rest energy of the planet $\tilde{\mathcal{L}}=\tilde{\mathcal{L}}(x,\theta ,\dot{x},\stackrel{\cdot }{\theta }$ was proposed in order to have the associated Euler-Lagrange equations where is possible to define the associated momentum with respect to the variable $\theta$  as$\frac{\partial \tilde{\mathcal{L}}}{\partial \theta }={\tilde{P}}_{\theta }.$

For the proposed analysis we have set ${\tilde{P}}_{\theta }=L/m{c}^2=l/c^2$ , where $l=L/m$ . Notice that, the angular equation associated with the motion can be casted as

$\frac{\partial \tilde{\mathcal{L}}}{\partial \dot{\theta }}=\frac{\dot{\theta }{\tau }^2{x}^2}{\sqrt{1-{\tau }^2\left({\dot{x}}^2+x^2{\dot{\theta }}^2\right)}}={\tilde{P}}_{\theta }.$

Hence,

$\dot{\theta }=\frac{\tilde{P}\theta }{\tau x}\sqrt{\frac{1-{\tau }^2{\dot{x}}^2}{\left[{\tau }^2{x}^2+{\tilde{P}}_{\theta }^2\right]}}.$

We may use this relation to adjust $\tilde{\mathcal{L}}$ as

$\tilde{\mathcal{L}}=-{\left[1-{\tau }^2\left({\dot{x}}^2+\frac{{\tilde{P}}_{\theta }^2}{{\tau }^2}\frac{\left(1-{\tau }^2{\dot{x}}^2\right)}{\left[{\tau }^2{x}^2+{\tilde{P}}_{\theta }^2\right]}\right)\right]}^{1/2}+\alpha \frac{1}{x}. (3)$

Now it is possible to determine the correspondent radial equation associated with the planet motion as

$\ddot{x}=\frac{1}{\Xi }\left\{\left[\frac{x{\tau }^2\left(1-{\dot{x}}^2{\tau }^2\right)}{{\gamma }^2\left(x^2{\tau }^2+{\tilde{P}}_{\theta }^2\right)}-\frac{1}{x}\right]\frac{{\tilde{P}}_{\theta }^2{\dot{x}}^2}{\left({\tilde{P}}_{\theta }^2+{\tau }^2{x}^2\right)}+\frac{{\tilde{P}}_{\theta }^2}{\left({\tilde{P}}_{\theta }^2+{\tau }^2{x}^2\right)x{\tau }^2}-\frac{\alpha \left(x^2{\tau }^2+{\tilde{P}}_{\theta }^2\right)\gamma }{{\tau }^4{x}^4}\right\},$

Where

$\gamma =\sqrt{1-{\tau }^2\left({\dot{x}}^2+\frac{{\tilde{P}}_{\theta }^2}{{\tau }^2}\frac{\left(1-{\tau }^2{\dot{x}}^2\right)}{\left[{\tau }^2{x}^2+{\tilde{P}}_{\theta }^2\right]}\right)}$

And

$\text{Ξ}=\left(1+\frac{{\dot{x}}^2}{{\gamma }^2}\frac{x^2{\tau }^4}{x^2{\tau }^2+{\tilde{P}}_{\theta }^2}\right).$

The last procedure to convert the related equation into a pure dimensionless form is to redefine$\text{t=t=}\tau$ , then

$t=\tau \tilde{t}, \frac{d}{dt}=\frac{1}{\tau }\frac{d}{d\tilde{t}}, \frac{d^2}{d{t}^2}=\frac{1}{{\tau }^2}\frac{d^2}{d{\tilde{t}}^2}, P_{\theta }^{*}=\frac{P_{\theta }}{\tau }.$

Now, the equations of motion can be written as

$\dot{\theta }=\frac{P_{\theta }^{*}}{x}\sqrt{\frac{1-{\dot{x}}^2}{\left[x^2+P_{\theta }^{*2}\right]}}. \left(4\right)$

$\theta \approx 0.42rad$

with

$\text{Ξ}=\left(1+\frac{{\dot{x}}^2}{{\gamma }^2}\frac{x^2}{x^2+P_{\theta }^{*2}}\right) \left(6\right)$

$\gamma =\sqrt{1-\left({\dot{x}}^2+P_{\theta }^{*2}\frac{\left(1-{\dot{x}}^2\right)}{\left[x^2+P_{\theta }^{*2}\right]}\right)} \left(7\right)$

The proposed differential equations are very similar to the first-order orbit equations proposed by D’Eliseo.²² In order to determine the initial values of ${{\rm P}}_{\theta }^{*}$ firstly, we must determine the correspondent module of the angular momentum

$l=\frac{L}{m}=b\sqrt{\frac{GM}{a}}, P_{\theta }^{*}=\frac{1}{\tau c^2}$

where a is the semimajor-axis of the ellipse and b the semiminor-axis, given by $b=a\sqrt{1-{\epsilon }^2}$ , with $\epsilon$ being the elongation of the ellipse. The initial associated radial velocity $\dot{x}=0$ was determined as

$\dot{x}={\left(\frac{v^2{\tau }^2}{R_0^2}-\frac{P_{\theta }^{*2}}{x^2+P_{\theta }^{*2}}\right)}^{1/2}.{\left(1-\frac{P_{\theta }^{*2}}{x^2+P_{\theta }^{*2}}\right)}^{-1/2}$

the initial position r(0) was considered as the perihelion where the velocity of the planet is maximum.

At the next section we shall determine some of the orbit trajectories associated with Mercury.

The motion equations integration was performed using numerical techniques Runge Kutta Fehlberg (RKF-45)²³ with variable integration step. Given the nonlinearity of the obtained motion equations that are quite different from the ones obtained in literature, for example, by the first-order approximation method proposed by D’amour and Derelle.²⁴ The precision requirement for the RKF45 were chosen as maximum error ${10}^{-8}$ per step, and maximum number of iterations of ${10}^6$ per step. The implementation and validation of the code produced was performed with an accurate comparison between the results obtained with similar nonlinear deferential equations solved by the function ODE2 from the WxMaxima software.²⁵

Considering the parameters shown in (Tables 1&2) the motion equations were integrated until the planet complete one revolution1 (1The integration starts at angular position $\theta (0)=\pi$ ). A typical result comparing the classical and the relativistic approximation can be observed at Figure 2 and a magnification of the radial difference at the trajectories is presented in Figure 3.

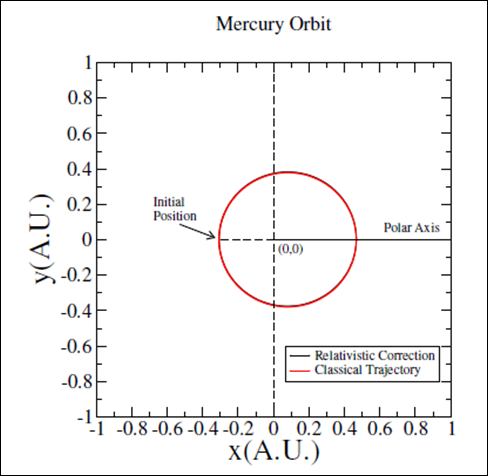
Figure 2 Mercury orbit at Cartesian coordinates system, the red curve represents the classical elliptical orbit, and the black curve represents the orbit with the proposed relativistic correction.

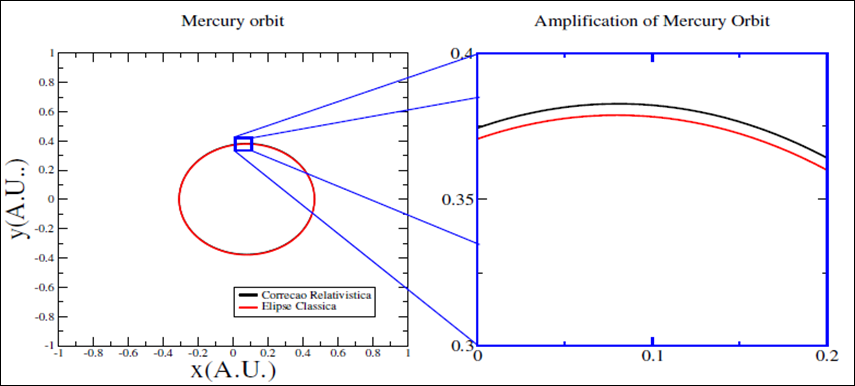
Figure 3 Mercury orbit at cartesian coordinates system, the red curve represents the classical elliptical orbit, and the black curve represents the orbit with the proposed relativistic correction. It is shown a magnification at the region near of angular position $3\pi /2$ , where the separation and divergency between the two orbits are more visible.

We have also determined the radial difference defined $\delta R(\theta )\equiv R_{cla}(\theta )-R_{rel}(\theta )$  between the classical $R_{cla}$ and relativistic corrected trajectories$R_{rel}$ . This result is shown in Figure 4.

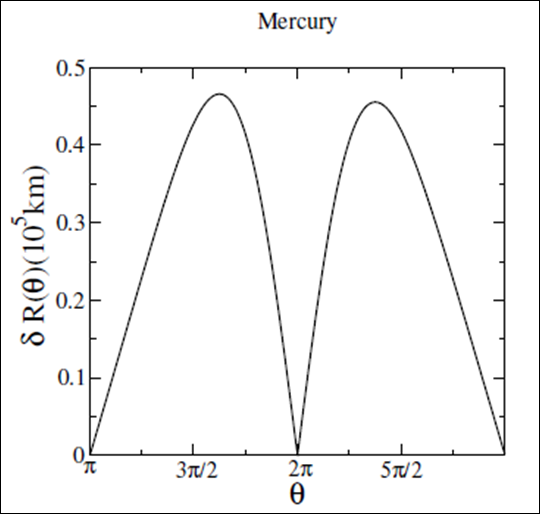
Figure 4 Determination of the radial difference between the classical and the relativistic corrected trajectory, as a function of $\theta$ for one revolution of Mercury.

The difference between the two trajectories can be detected even for the polar plot of the associated radial position x (t) and at the angular position $\theta \left(t\right)$  as depicted in Figure 5.

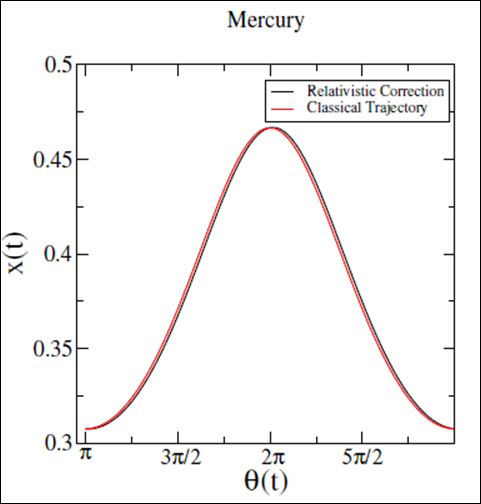
Figure 5 Graphic $x(t)\times \theta (t)$ for one revolution of Mercury. Here is possible to observe the none asymptotic behavior the trajectories. The red curve represents the classical trajectory and the black curve represents the relativistic corrected trajectory.

Another graphic where is possible to visualize the difference between the classical and the relativistic correction at the trajectories is the Phase Space associated with the variable x, this plot $\dot{x}\times x$ can be seen in Figure 6. Notice that, for a typical elliptic trajectory the curve at the phase space would be approximately a circle that is completely different from the D-shaped curve observed in Figure 6.

Figure 6 Phase Space Diagram, associated with the variable x(t) one revolution of Mercury

The mercury precession

The precession of a planet occurs taking into account the center of a reference frame, in this case the sun. Similar to the geometrical procedure observed at Figure 7, after some time $\stackrel{\sim }{{\displaystyle T}}$ , given the influence of pure relativistic influence, the planet may change the plane of its trajectory realizing a certain precession, with respect to the$\varphi$ angle. To determine this precession angle, we get the perihelion and the aphelion belonging to a line that contains the Sun, at the initial orbit (first revolution) and at the final orbit (last revolution) and determine the relative inclination angle.

For Mercury the angle $\varphi$ as a function of the revolutions can be observed at Figure 8, where after 400 revolutions are approximately $\varphi 400\approx 43\text{'}\text{'}$ , which is a very close result when compared to the value predicted by general relativity. Hence, we could say that the perturbation procedure here proposed is a very good approximation to determine the influence of general relativity using a more simple mathematical approach from the point of view of theoretical physics.

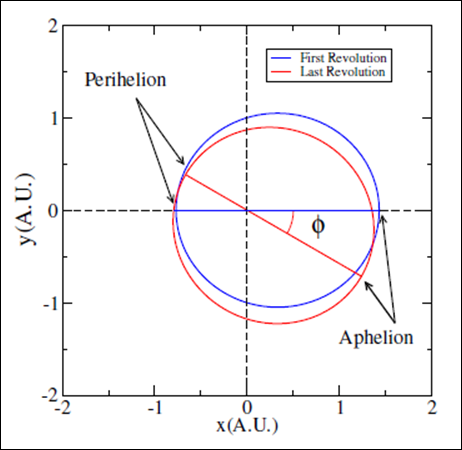
Figure 7 Schematic diagram to determine the precession effect at the planets orbits due to the relativistic correction of the orbits.

Figure 8 Determination of the precession angle $\varphi$ as function of the number of revolutions n, for Mercury. The approximate value of $\varphi (200)\approx 43\text{'}\text{'}$ quite agrees with the expected value predicted by general relativity 0.4

Considering the precession imposed by the relativistic correction term, we can observe that Mercury’s orbit is not intrinsic periodic, since the set of points associated with the Poincare’ map - see Figure 9 - related to the variables $(\theta ,\theta )$ do not have a finite dimension, on other words, in spite of the huge number of revolutions computed, the object (Mercury) do not recover the exactly same dynamical configuration. As predicted by the KAM theorem,¹⁵ it is a purely chaotic dynamical system, even for just one interaction between the planet and the sun. These chaotic approaches have not been discussed by other studies.^12,13,21,22 Otherwise, as can be observed, the present work gives rise for new investigations from the perspective of stability and nonlinear phenomena.

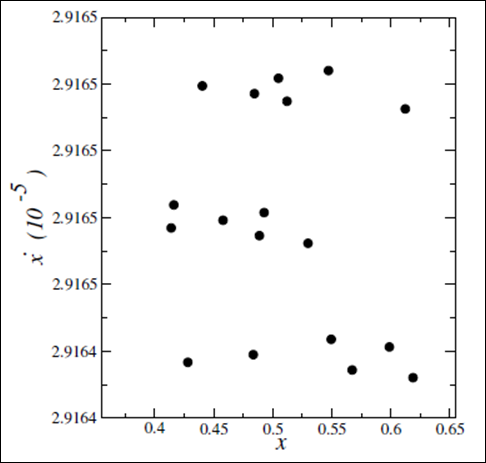
Figure 9 Determination of the Poincare Map for the Mercury trajectory over approximately 200 years. Under the position $\theta \approx 0.42rad$ .

A more precise approximation could be performed taking into account the interaction between more than two bodies. For example, considering the interactions with Saturn and Jupiter.

The relativistic celestial dynamic correction proposed by an effective relativistic Lagrangean, built with a proper classical gravitational potential, can recover, with a good numerical accuracy, the orbits obtained by general relativity, which calculations are quite more complex to perform. Given the proximity of Mercury to the Sun, the analysis of its perihelion precession through 100 years achieved good agreement with the experimental result $\varphi \approx 43\text{'}\text{'}s$ . In addition, from the perspective of nonlinear dynamic, the Poincare’ map with a huge number of points for the same angular orbit plane, shows a non periodic motion by a nonlinear as predicted by the KAM theorem, showing that is possible to investigate this nonlinear phenomena with other numerical and theoretical tools, even when classical interaction potentials are used.

We would like to thanks the Federal Institute of Education, Science and Technology of Espírito Santo for the opportunity and the Brazilian agency CNPq for the financial support.