A pressure-less flat-dust universe model is an oversimplification solution to the Einstein's Field equations. This led to a drastic failure in predicting the missing mass and the accelerating expansion of the universe. Geometry is the study of the local structures of the manifold, by means of measurement and observations. Topology is the study of the global structures of the manifold, mathematically. In General Relativity Theory, gravity is geometry. In order to modify the laws of gravity; a natural first step is to modify the geometry itself. Hence, we develop the modified laws of gravity from the updated non-Euclidean geometry. We propose that the geometry of the universe is globally hyperbolic. We develop the laws of gravity in the hyperbolic space-time. Such laws fit the current observed data and ruling out both dark matter and dark energy. Hence, the universe is not dark.

Keywords: hyperbolic universe modified gravity, dark matter, dark energy

Cosmology, in its broadest definition, is the study of the cosmos. It aims to provide an accurate description of the universe. Throughout much of the history of science, the development of cosmology was hampered by the lack of a universal physical theory. Observational tools were extremely limited, and there was no mathematical formulation for physical laws. Cosmology depends upon a fundamental premise. As a science, it must deal strictly with what can be observed, but the observable universe forms only a fraction of the whole cosmos. One is forced to make the fundamental but unverifiable assumption that the portion of the universe which can be observed is representative of the whole universe, and that the laws of physics are the same throughout the whole universe. Once we make this assumption, we can construct a model of the universe based on a description of its observable part.¹ The satellite"s observations of the cosmic microwave background radiation (CMB) indicate that the universe is geometrically –locally- flat, or pretty close to it. Not even perfectly flat. In the flat Universe where the curvature is zero and the density is the critical density, new hypothetical objects, dark energy and dark matter are essential to bridge the gap between theory and observation. It is clear that these new ingredients, dark energy and dark matter, arose as a consequence to the false flat universe paradigm. Without them, there would be a fatal contradiction between the observations made by astronomers and the predictions of the Big Bang Theory.² The realization from the rotation curves of galaxies that there is considerably more matter with attractive gravity, called dark matter, than we can see via electromagnetic radiation (the visible matter) complicates things. With attractive gravity between the components of the universe the expectation was that the expansion velocity of the universe, the so called Hubble velocity, would decrease with time, i.e. a decelerating universe. The recent discovery that the Hubble velocity is increasing with time, an accelerating universe, was an immense surprise. This led to the postulation of the existence of a new component of the universe, dark energy, with some very unusual properties, not the least among which is that it has, in some sense of the word, repulsive gravity that drives the acceleration. A flat-dust universe with zero pressure models is an oversimplification solution to the Einstein's Field equations. This led to drastic failure in predicting the missing mass and the accelerating expansion of the universe. We may question the accuracy of our solutions to the equations of General Relativity, which depend on some approximation scheme. These approximations provided analytical solutions which enabled most of the early progress in General Relativistic cosmology and astrophysics. We may question whether General Relativity is valid, given that the universe cannot be modeled sufficiently accurately by General Relativity without invoking either a cosmological constant, or some additional, unknown component of the universe. We modify the laws of gravity based on a hyperbolic spacetime rather than a flat spacetime.³ Such a modification explains the accelerating expansion of the Universe without need for dark energy and inflation and also explains the flat rotation curve without need for dark matter. Although perspective for nearby objects in hyperbolic space is very nearly identical to Euclidean space (i.e. the geometry of the Universe locally is approximately flat consistent with local observations), the apparent angular size of distant objects falls off much more rapidly, in fact exponentially. The topology of the Universe globally is hyperbolic as proposed and analysed mathematically "The Hyperbolic Geometry of the Universe and the wedding of General Relativity Theory to Quantum Theory”.⁴ The Hyperbolic Universe solution predicts the equation of state of cosmology, P = −ρ, consistent with accelerating expansion. The hyperbolic structure of the spacetime causes the accelerated expansion of the universe equivalent to its negative pressure.

"The accelerating expansion of the universe was discovered when astronomers were doing research on type 1a supernova events.⁵ Because all type 1a supernova explosions are remarkably similar in brightness, if we know how bright a star should be, we can compare the apparent luminosity with the intrinsic luminosity, and we get a reliable figure for how far any given object is from us. Incidentally, along with helping us make these key determinations about the locations of objects in the universe, these supernova explosions also gave us a sneak preview of one of the strangest observations ever made about the universe. To measure the approximate distance of an object, like a star, and how that distance has changed, astronomers analyze the spectrum of light emitted. Scientists were able to tell that the universe is increasing in expansion because, as the light waves make a long journey to Earth−billions of light-years away−the universe continues to expand. And as it expands, it stretches light and all electromagnetic waves through the process of redshifting towards longer wavelengths (“red” by analogy with the longest wavelength of visible light). The more redshifted this light is, the faster the expansion is inferred to be”. Many years of painstaking observations (made by many different astronomers) have confirmed that this expansion is still ongoing and increasing because (as previously mentioned) the farther away an object is, the more redshifted it is, and (thus) the faster it is moving away from us".⁶ The 1990's two teams of astronomers, the Supernova Cosmology Project (Lawrence Berkeley National Laboratory) and the High-Z Supernova Search (international) were looking for distant Type Ia supernovae in order to measure the expansion rate of the Universe with time.⁷−⁹ They expected that the expansion would be slowing, which would be indicated by the supernovae being brighter than their redshifts would indicate. Instead, they found the supernovae to be fainter than expected from a uniformly expanding universe. Hence, the expansion of the Universe was accelerating! Anyone with even a passing interest in space science is familiar with this unforeseen development that occurred in 1998. In that year the research focuses into the decay of distant supernovae events revealed that these objects are actually considerably farther from us than had been expected. The findings were so contrary to theory that at first there was considerable doubt. It was only after another study, by an independent team " High-Z Supernova Search (international)",⁹ came to the same conclusion (that these "standard candle" exploding stars were 20% to 25% farther than expected) that the crisis hit home. The standard theories of the universe, the hot big bang model and inflationary big bang model, had predicted that the matter in the universe thrown out by the "big bang" should decelerate as gravity acts to slow down this matter and eventually pull it all inward in a "big crunch." But now, it seems, the opposite is true: the speed of expansion of the universe is increasing! Mysteriously, the universe is now accelerating −or so it is believed. And so, in 1998 astronomers and physicists convinced themselves that the universe is accelerating −getting bigger and bigger, faster and faster. Now there is a new mystery! What"s driving this thing? Why is the universe accelerating? You can coast along on "expansion" but you need a force when you bring in "acceleration." No exception. Forget the minimal mystery of why the universe is expanding in the first place; now there is the utterly baffling mystery of why it is expanding with a vengeance! In other ways this new dark [acceleration leads to dilution which leads to darkness] universe is utterly baffling, a road map to new mysteries. Dr. Marc Davis, a cosmologist at the University of California at Berkeley, called it "a universe chock full of exotics that don"t make sense to anybody (Figure 1)."⁸

Figure 1 Type 1a supernova depicted here at the lower left hand corner. Image credit: High-Z Supernova Search Team, HST, NASA.⁹

The hyperbolic universe inflates exponentially producing an accelerated expansion of the universe without cosmological constant or scalar field. We have shown that general relativity doesn"t break down at large cosmological scale since it predicts both the accelerated expansion of the universe (without invoking dark energy) and predicts the galaxy flat rotation curve (without invoking dark matter). General relativity didn"t break down at Planck scale as we had shown.⁴ The Type 1a supernova as standard candles can be used to measure the expansion history of the universe i.e. the plot of the scale factor of the universe when the supernova light was emitted versus the time in the past when the supernova explosion occurred. This is done by measuring the apparent brightness L of the supernova and its redshift z. Comparing the apparent brightness to the presumably known intrinsic brightness of the supernova determines its distance and from the distance the time in the past when the supernova exploded can be inferred knowing the velocity of light. The redshift gives the scale factor of the universe at the time of the supernova explosion via a(t) = 1/(1+z). Each supernova then yields a point in the a(t) versus t plot, and a large sample of supernovae thus measure the expansion history of the universe. Given the high level of interest in understanding the underlying reasons for the acceleration of the universe and the nature of dark energy, a vigorous program is planned worldwide to measure the cosmological parameters to a higher level of precision. In particular there is a focus on the measurement of the equation of state parameter w, which can distinguish between a cosmological constant (w= − 1) or some other form of dark energy with $w<-1/3$ but not exactly −1. The present dependence of w, which would be inconsistent with a cosmological constant, is very poorly constrained by the present data. It is results, w = −0.93±0.16 is consistent with the cosmological constant but higher precision may yet show a deviation from −1. The parameter wa that dark energy is due to a nonzero cosmological constant, a value of ΩΛ in the vicinity of 0.7 would be implied. Such a small value of ${\Omega }_{\Lambda }$ would lead to one of the most dramatic inconsistencies in modern physics called the cosmological constant problem. Modern field theory of particle physics predicts that the energy density of the vacuum contributes to the cosmological constant with a value 120 orders of magnitude larger than the experimentally observed value. Actually this problem would persist even if the dark energy turned out to be something else than the cosmological constant, with $\Lambda =0$. Even though many theorists have tried, there is no explanation in sight to this fundamental disagreement. Accelerating, ruling out a nonaccelerating universe and a zero cosmological constant with a very high level of confident. All of the surveys are consistent with w = −1, assuming a constant w and a flat universe. We exhibit the hyperbolic structure of the universe that explains the accelerating expansion of the universe without need for an additional components, dark energy and dark matter (Figure 2).¹⁰

Figure 2 In the Euclidean geometry space is divided into cubes and one experiences the ordinary, familiar perspective: the apparent angular size of objects is proportional to the inverse of their distance. Stuart Levy of the University of Illinois, Urbana-Champaign and Tamara Munzer of Stanford University.¹⁰

In addition, measurements of the cosmic microwave background indicate that the Universe has a flat geometry on large scales. Because there is not enough matter in the Universe either ordinary or dark matter to produce this flatness, the difference must be attributed to a "dark energy". This same dark energy causes the acceleration of the expansion of the Universe. In addition, the effect of dark energy seems to vary, with the expansion of the Universe slowing down and speeding up over different times. One explanation for dark energy is that it is a property of space. The simplest explanation for dark energy is that it is simply the "cost of having space": that is, a volume of space has some intrinsic, fundamental energy.

Some astronomers identify dark energy with Einstein`s Cosmological Constant. In the context of dark energy, the cosmological constant represents (mathematically) energy that scales as the Universe expand, like dark energy. Applied to the supernova data, it would distinguish effects due to the matter in the Universe from those due to the dark energy. Another explanation for how space acquires energy comes from the quantum theory of matter. In this theory, "empty space" is actually full of temporary ("virtual") particles that continually form and then disappear. But when physicists tried to calculate how much energy this would give empty space, the answer came out wrong-wrong by a lot. The number came out 10¹²⁰times too big. Particle physics predicts a natural value of 1 in reduced Planck units, leading to a large discrepancy. It's hard to get an answer that bad. More recently, the WMAP seven-year analysis gave an estimate of 72.8% dark energy, 22.7% dark matter and 4.6% ordinary matter. The cosmological constant has negative pressure equal to its energy density and so causes the expansion of the universe to accelerate. The reason why a cosmological constant implies has negative pressure can be seen from classical thermodynamics; Energy must be lost from inside a container to do work on the container. A change in volume dV requires work done equal to a change of energy −P dV, where P is the pressure. But the amount of energy in a container full of vacuum actually increases when the volume increases (dV is positive), because the energy is equal to $\text{ρV}$, where $\text{ρ}$ is the energy density of the cosmological constant. Therefore, P is negative and, in fact, P = $-\rho$.

An alternative hypothesis is provided by a time-dependent homogeneous minimally coupled scalar field $\varnothing \left(t\right)$ called Quintessence It is well known that such a field can be viewed as a commoving perfect fluid with

$\begin{array}{ccc}{\rho }_{\varphi }=\frac{1}{2}\dot{\varphi }+V\left(\varphi \right)& and& p_{\varphi }=\frac{1}{2}\dot{\varphi }-V\left(\varphi \right)\end{array}$      (1)

Where p is the pressure and ρ is the energy density. Hence the corresponding equation of state parameter is

$\begin{array}{cc}{w}_{\varphi }=\frac{p_{\varphi }}{{\rho }_{\varphi }}=& \left(\frac{1}{2}\dot{\varphi }-V\left(\varphi \right)\right)/\left(\frac{1}{2}\dot{\varphi }+V\left(\varphi \right)\right)\end{array}$          (2)

We see that ${\text{w}}_{\varnothing }$  can be sufficiently negative in this case provided the kinetic energy is small enough compared to the potential energy. This mechanism is actually used in implementing the inflationary scenario in the very early universe. Though ${\text{w}}_{\varnothing }$  is generically dynamical, it can never cross the boundary w=−1 a. Hence time-varying equation of state parameter is a natural outcome for quintessence models with the important restriction that there is no phantom phase.¹¹

f(R) gravity is a class of effective theories representing a new approach to the gravitational interaction. The paradigm is that Einstein's General Relativity has to be extended in order to address several shortcomings emerging at ultraviolet and infrared scales. These are essentially due to the lack of a final, self-consistent theory of quantum gravity. From the astrophysical and cosmological viewpoints, the goal is to encompass phenomena like dark energy and dark matter under a geometric standard related to the possibility that gravitational interaction depends on the scales. This geometric view, in principle, does not need the introduction of further particle ingredients and preserves all the well-posed results of General Relativity, being based on the same fundamental principles (Equivalence Principle, diffeomorphism invariance, gauge invariance, etc.). The main criticism to this approach is that, until now, no f(R) model, or any Extended Theory of Gravity, succeeds in addressing the whole phenomenology ranging from quantum to cosmological scales. Besides, the f(R) description of dark side of the universe is substantially equivalent to that related to the hypothesis of dark material constituents. The recently reported gravitational wave detection, GW170817, was accompanied by electromagnetic radiation.¹¹ Both signals arrived on Earth almost simultaneously, within a time-window of a few seconds. The observation is difficult to explain with some variants of modified gravity because in these models electromagnetic and gravitational radiation travel differently. This is a big problem for some alternatives to dark matter (such as Bekenstein"s TeVeS and Moffat"s Scalar-Vector-Tensor theory) as this new paper lays out: GW170817 Falsifies Dark Matter Emulators (Figure 3).¹²

Figure 3 Hyperbolic space shown here is tiled with regular dodecahedra. In Euclidean space such a regular tiling is impossible. The size of the cells is of the same order as the curvature scale. Although perspective for nearby objects in hyperbolic space is very nearly identical to Euclidean space, the apparent angular size of distant objects falls off much more rapidly, in fact exponentially, as can be seen in the figure. Stuart Levy of the University of Illinois, Urbana-Champaign and by Tamara Munzer of Stanford University.¹⁰

Although perspective for nearby objects in hyperbolic space is very nearly identical to Euclidean space (i.e. the Universe locally is approximately flat consistent with local observations), the apparent angular size of distant objects falls off much more rapidly, in fact exponentially. The Universe is globally hyperbolic as we proposed and analysed mathematically. Such a solution predicts the equation of state of cosmology. We solved the dynamical equations of cosmology (Friedmann`s equation)⁴

${\dot{R}}^2+k=(8\pi /3)\rho R^2$       (3)

$2R\ddot{R}+{\dot{R}}^2+k=-8\pi p{R}^2$    (4)

Where R is the scale factor, p is the pressure, $\rho$ is the energy density of the cosmological fluid and k is the curvature. We use c=G=1. The solution of Eq. (3), is

$R=-i\sqrt{3k/8\pi {\rho }_j}\sinh t\sqrt{8\pi {\rho }_j/3}$

A simple analysis shows that R(t), the scale factor, represented in the last equation is complex if k is positive, vanishes if k is zero and positive if k is negative. Since k is normalized, k = -1 in order R(t) to be positive, real and nonzero.

$\begin{array}{l}k=\text{-}1\\ R=\sqrt{3/8\pi {\rho }_j}\sinh t\sqrt{8\pi {\rho }_j/3}\end{array}$          (5)

Hence the universe is hyperbolic.

Note that the solution represented by Eq. (5) is evaluated only for the values simultaneously associated with,

${\rho }_j$ namely $\left(R_j,t_j\right)$

$R_j=\sqrt{3/8\pi {\rho }_j}\sinh t_j\sqrt{8\pi {\rho }_j/3}$               (6)

Eq. (6) is valid at the Planck scale, since it exactly predicts the Planck length. Substitute Planck density (3.8789×10⁶²cm) and Planck time (5.4×10^-44 ×2.997×10¹⁰cm) ,in geometrical units, in the RHS of Eq. (6):

$\begin{array}{l}{R}_p=\sqrt{3/8\pi \times 3.8789\times {10}^{62}}\sinh [5.4\times {10}^{-44}\times 2.997\times {10}^{10}\\ \times \sqrt{8\pi \times 3.8789\times {10}^{62}/3}]=1.62\times {10}^{-33}cm=L_p\end{array}$    (7)

We shall see that the solution of equation (4) satisfies the second order differential equation (5) in order to be consistent. We have from the solution of Eq. (4) for any chosen value ${\rho }_j$ .

$R=\sqrt{\frac{3}{8\pi {\rho }_j}}\sinh t\sqrt{\frac{8\pi {\rho }_j}{3}}$    (8)

$\dot{R}=\cosh t\sqrt{\frac{8\pi {\rho }_j}{3}}$                                                                              (9)

$\ddot{R}=\sqrt{\frac{8\pi {\rho }_j}{3}}\sinh t\sqrt{\frac{8\pi {\rho }_j}{3}}=\frac{8\pi {\rho }_j}{3}R$        (10)

Substitute these values in Eq. (2), and put $k=-1$ , yields:

$2R\stackrel{\mathrm{..}}{R}+{\dot{R}}^2-1=-8\pi p{R}^2$       (11)

$2R\left(\frac{8\pi {\rho }_j}{3}R\right)+{\cosh }^2\sqrt{\frac{8\pi {\rho }_j}{3}}-1=-8\pi p{R}^2$         (12)

$2R^2\left(\frac{8\pi {\rho }_j}{3}\right)+{\sinh }^2\sqrt{\frac{8\pi {\rho }_j}{3}}=-8\pi p{R}^2$          (13)

$2R^2\left(\frac{8\pi {\rho }_j}{3}\right)+\frac{8\pi {\rho }_j}{3}{R}^2=-8\pi p{R}^2$           (14)

$\begin{array}{l}8\pi {\rho }_j{R}^2=-8\pi p{R}^2\\ p=-{\rho }_j\end{array}$             (15)

Friedmann`s equation in the presence of the cosmological constant are given by

${\dot{R}}^2+k-\Lambda R^2/3=(8\pi /3)\rho R^2$     (16)

$2R\ddot{R}+{\dot{R}}^2+k-\Lambda R^2=-8\pi p{R}^2$   (17)

$\because \Lambda =8\pi {\rho }^{{}^{vacuum}},k=-1$              (18)

${\dot{R}}^2-1-8\pi {\rho }^{{}^{vacuum}}{R}^2/3=(8\pi /3)\rho R^2$         (19)

$2R\ddot{R}+{\dot{R}}^2-1-8\pi {\rho }^{{}^{vacuum}}{R}^2=-8\pi p{R}^2$      (20)

The solution of Eq. (19), is

$R=\sqrt{3/8\pi \left({\rho }^{{}^{vacuum}}+{\rho }_j\right)}\sinh t\sqrt{8\pi \left({\rho }^{{}^{vacuum}}+{\rho }_j\right)/3}$        (21)

Substitute Eq. (21) in Eq. (20)

$8\pi \left({\rho }^{vacuum}+{\rho }_j\right)R^2-8\pi {\rho }^{{}^{vacuum}}{R}^2=-8\pi p{R}^2$           (22)

${\rho }^{vacuum}+{\rho }_j-{\rho }^{{}^{vacuum}}=-p$             (23)

$\therefore p=-{\rho }_j$     (24)

So the cosmological constant (the vacuum energy) disappeared in the solution of the second differential Eq. (20). Just the ordinary energy density state ${\rho }_j$  remains in the Hyperbolic Universe to derive the accelerating expansion equivalent to its negative pressure. Hyperbolic Universe involves zero¹³ cosmological constant (the vacuum energy). The negative pressure $p=-{\rho }_j$  is the property of the hyperbolic structure of the Universe. The hyperbolic structure of the space-time –not the cosmological constant- causes the apparently observed accelerating expansion of the Universe (Figure 4).¹⁴

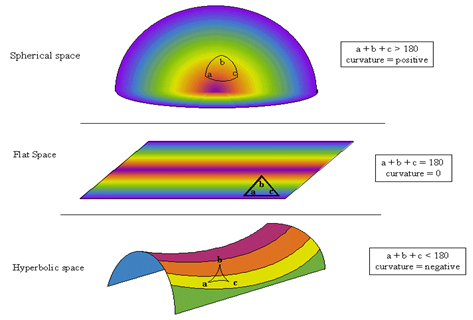
Figure 4 Curvature of space-time. Martha Haynes and Stirling Churchman.⁴

Zero pressure-dust universe is decelerating universe:Einstein postulates¹⁵ that the matter dominated universe could be modeled as dust with zero pressure in order to simplify and solves Friedmann`s equations.

${\dot{R}}^2+k=(8\pi /3)\rho R^2$      (25)

$2R\ddot{R}+{\dot{R}}^2+k=0$      (26)

$\therefore 2R\ddot{R}=-(8\pi /3)\rho R^2$        (27)

$\therefore \ddot{R}=-(4\pi /3)\rho R<0$       (28)

Guarantees a decelerating expansion of the universe. The pressureless form, Eq. (26), describes a decelerating expansion state of the universe which is described by the energy tensor of matter for dust where $\rho =0.$  We solved the second dynamical equation of cosmology in it is pressureless form:

$2R\ddot{R}+{\dot{R}}^2-1=0$           (29)

$\therefore R=t$       (30)

Substitute $R=t$  and k = -1 in Eq. (25)

${\dot{R}}^2+k=(8\pi /3)\rho R^2$        (31)

$\therefore 1-1=(8\pi /3)\rho t^2$         (32)

$\therefore \rho =0$       (33)

Hence the zero pressure does not lead to a dusty universe. In fact a zero pressure Universe is an empty space, since $\rho =0.$  In the presence of pressure, the hyperbolic universe possesses an accelerated expansion as follows;

${\dot{R}}^2+k=(8\pi /3)\rho R^2$      (34)

$2R\ddot{R}+{\dot{R}}^2+k=-8\pi p{R}^2$    (35)

$\begin{array}{l}\therefore \ddot{R}=-\frac{4\pi }{3}\left(3p+\rho \right)R\\ \because p=-\rho \end{array}$      (36)

$\therefore \ddot{R}=\frac{8\pi }{3}\rho R>0$        (37)

Guarantees an accelerated expansion of the Universe. Moreover the hyperbolic evolution equation of the Universe predicts the large structure of the observable

Universe 10²⁸cm associated with 14 × 10⁹ yr.³. Note

1 sec = 2.997×10¹⁰cm

1 gram = 7.425×10^-29cm

1 yr = 3.16×10⁷ s

The age of the Universe (approximately) $t_{now}=14\times {10}^{9}yr$

Substitute the above data in the hyperbolic time evolution equation of the Universe, yields

$R_j=\sqrt{3/8\pi {\rho }_j}\sinh \left[t_j\sqrt{8\pi {\rho }_j/3}\right]$

$R_{now}=\sqrt{3/8\pi {\rho }_{now}}\sinh \left[t_{now}\sqrt{8\pi {\rho }_{now}/3}\right]$

$\begin{array}{l}{R}_{now}=\sqrt{3/\left(8\pi \times 7.425\times {10}^{-60}\right)}\times \\ \sinh \left[\begin{array}{l}{\text{14×10}}^{\text{9}}\times 3.16\times {10}^7\times \text{2}{\text{.997×10}}^{\text{10}}\\ \times \sqrt{8\pi \times 7.425\times {10}^{-60}/3}\end{array}\right]\end{array}$            (38)

$R_{now}=1.6\times {10}^{29}\times \sinh 0.08287$         (39)

$R_{now}=1.3\times {10}^{28}cm$     (40)

Newton`s laws of gravity do no longer hold in non-Euclidean geometry. Geometry is the study of the local structures of the manifold, by means of measurements and observations. Observations being made are not complete in themselves; they interpreted within a theory (a paradigm). Topology is the study of the global structures of the manifold, mathematically. In General Relativity Theory, gravity is geometry. In order to modify the laws of gravity; first we should modify the underlying geometry itself.¹⁵ Hence, we establish the modified laws of gravity from the updated non-Euclidean geometry. We prove that the topology of the universe is globally hyperbolic. We develop the laws of gravity in the hyperbolic spacetime. Such modified laws fit the current observed data and successively predict the accelerated expansion of the universe without invoking Dark Energy. The observed average density of the universe is 3x10-31g/cm3. This density implies an open universe (hyperbolic universe) (Table 1).¹⁶

A general observation of galaxy rotation can be stated as: galaxies with a central bulge in their disk have a rotation curve which is flat from near the centre to the edge, i.e. stars are observed to revolve around the centre of these galaxies at a constant speed over a large range of distances from the centre of the galaxy. However, it was expected that these galaxies would have a rotation curve that slopes down from the centre to the edge in the same way as other systems with most of their mass in the centre, such as the Solar System of planets or the Jovian System of moons following the prediction of Kepler's Laws. Something else is needed to account for the dynamics of galaxies besides a simple application of the laws of gravity to the observed matter. It is also observed that galaxies with a uniform distribution of luminous matter have a rotation curve sloping up from center to edge. Most low surface brightness galaxies rotate with a rotation curve that slopes up from the center, indicating little core bulge. The galaxy rotation problem is the discrepancy between observed galaxy rotation curves and the ones predicted assuming a centrally-dominated mass that follows the luminous material observed. If masses of galaxies are derived solely from the luminosities and the mass-to-light ratios in the disk and core portions of spiral galaxies are assumed to be close to that of stars, the masses derived from the kinematics of the observed rotation do not match. This discrepancy can be accounted for if there exist a large amount of dark matter that permeates the galaxy and extends into the galaxy's halo. Many physicists are nowadays convinced that some form of dark matter has to exist to explain for instance the discrepancy between the flat rotation curves of stars within a galaxy and the rotation curves expected from Kepler's third law. Assuming flat space and circular orbit, astronomers use the Virial theorem to determine the masses of the galaxies: $\text{M}={\text{V}}^2\text{R}/\text{G}$ . M is the mass of the galaxy, V is the speed of the galaxy, R is the distance of the galactic center and G is the gravitational constant (Figure 5).¹⁷

Figure 5 The rotation curve of a galaxy (also called a velocity curve) is the plot of the orbital speed (in km/s) of the stars or gas in the galaxy on the y-axis against the distance from the center of the galaxy on the x-axis.¹⁷

Rotational Velocity: Using the power of the Doppler Shift, scientists can learn much about the motions of galaxies. They know that galaxies rotate because, when viewed edge-on, the light from one side of the galaxy is blue shifted and the light from the other side is red shifted. One side is moving toward the Earth, the other is moving away. They can also determine the speed at which the galaxy is rotating from how far the light is shifted. Knowing how fast the galaxy is rotating, they can then figure out the mass of the galaxy mathematically. As scientists look closer at the speeds of galactic rotation, they find something strange. The individual stars in a galaxy should act like the planets in our solar system, the farther away from the center, the slower they should move. But the Doppler Shift reveals that the stars in many galaxies do not slow down at farther distances. And on top of that, the stars move at speeds that should rip the galaxy apart; there is not enough measured mass to supply the gravity needed to hold the galaxy together. These high rotational speeds suggest that the galaxy contains more mass than was calculated. Scientists theorize that, if the galaxy was surrounded by a halo of unseen matter, the galaxy could remain stable at such high rotational speeds. Another method astronomers use to determine the mass of a galaxy (or cluster of galaxies) is simply to look at how much light there is. By measuring the amount of light reaching the earth, the scientists can estimate the number of stars in the galaxy. Knowing the number of stars in the galaxy, the scientists can then mathematically determine the mass of the galaxy. Astronomers use the Mass – Luminosity equation to determine the mass of a star $\text{M}=\sqrt[4]{\text{L}}$ . M=the star`s mass. L = the star`s Luminosity. Fritz Zwicky used both methods described here to determine the mass of the Coma cluster of galaxies over half a century ago. When he compared his data, he brought to light the missing mass problem. The high rotational speeds that suggest a halo reinforce Zwicky's findings. The data suggest that less than 10% of what we call the universe is in a form that we can see. Now scientists are diligently searching for the elusive dark matter, the other 90% of the universe. Throughout the 1970s, however, Rubin and other astronomers found the same pattern again and again, in galaxy after galaxy, until theorists had little choice but to reach a consensus: Galaxies are embedded within a vastly much larger, stabilizing halo of matter we can’t detect in any range of the electromagnetic spectrum −that is, matter that’s “dark.” Theorists even identified the properties of what the hypothetical matter might be, and experimenters began designing instruments that in principle would be able to detect the particle or collection of particles. Some theorists and observers have been pursuing that possibility since the early 1980s, though the community generally has seen their work as somewhat contrarian. The longer that dark matter went undetected, Rubin said, the more likely she thought the solution to the mystery would be a modification to our understanding of gravity. Maybe the discovery of dark matter was not possible. Maybe dark matter doesn’t exist. Maybe what she detected in the 1960s and 1970s was evidence that gravity doesn't work on large scales in the manner that Newton taught us.¹⁸

Most scientists think that dark matter is composed of non-baryonic matter. The lead candidate, WIMPS (weakly interacting massive particles), have ten to a hundred times the mass of a proton, but their weak interactions with "normal" matter make them difficult to detect. Neutralinos, massive hypothetical particles heavier and slower than neutrinos, are the foremost candidate, though they have yet to be spotted. The smaller neutral axion and the uncharched photinos are also potential placeholders for dark matter. Then there are the Weakly Interacting Massive Particles (WIMPs), which possess mass, yet do not interact with ordinary matter (baryons such as protons and neutrons) because they are composed by something unknown. Dark (missing) matter (DM) even comes in two flavors, hot (HDM) and cold (CDM). The CDM is supposedly to be in dead stars, planets, brown dwarfs ("failed stars") etc., while HDM is postulated to be fast moving in particles floating throughout the universe. It should be constituted by neutrinos, tachyons etc. But where is all of this missing matter? The truth is that after many years of looking for it, there is still no definitive proof that WIMPs exist. The latest results from two direct detection experiments have ruled out theoretically attractive dark matter candidates, including WIMPs. Scientists from two of the world"s biggest dark matter detectors have reported that their latest experiments, like all earlier attempts, have produced no sign of the elusive substance. Scientists from two of the world"s biggest dark matter detectors have reported that their latest experiments, like all earlier attempts, have produced no sign of the elusive substance. In a pair of papers published in Physical Review Letters, researchers from the XENON1T¹⁹ and PandaX-II²⁰ collaborations have ruled out some theoretical possibilities for dark matter particles.

There are the Massive Compact Halo Objects (MACHOs), objects like black holes, and neutron stars that purportedly populate the outer reaches of galaxies like the Milky Way. Some scientists are revisiting an old idea that black holes born at the dawn of time are a prime suspect for all that missing mass. Researchers call these speculative black holes "massive compact halo objects," or MACHOs, since dark matter lurks in a "halo" in and around big galaxies. But a new study in The Astrophysical Journal Letters offers a serious reality check to the idea that MACHOs are dark matter. Timothy Brandt, an astrophysicist at the Institute for Advanced Study, wrote the study after he took a close look at 11 dim, feeble, and weird little galaxies. The stars there are choking with dark matter, at least compared to larger galaxies like the Milky Way or Andromeda, but the little galaxies don't seem to show any obvious signs of harboring a flotilla of old black holes."These galaxies would be less dense and larger than we see," Brandt told Business Insider. Instead they're inexplicably compact. And that could represent a big threat to the MACHO hypothesis. Meanwhile, ultra-faint dwarf galaxies are roughly 99% dark matter."The dark matter is holding them together and preventing them from flying apart," Brandt told Business Insider. And that's where Brandt realized he could see if a bunch of old black holes between 20 to 100 times the mass of the sun (a size range for MACHOs that has yet to be ruled out) really exist there. If so, they'd accelerate stars as they passed nearby, causing the entire cluster or galaxy to "puff" outward over billions of years. A diffuse cloud of dark matter particles, on the other hand, would keep the cluster glued together.²¹ Most early massive galaxies are strongly dominated by normal matter: The theory is that galaxies contain dark matter and that this makes them gravitationally stable in the standard model of physics. McCulloch is skeptical about dark matter and he says that it is an implausible theory to explain dwarf galaxies, which are super-tiny galaxies containing only between 1,000-10,000 stars that revolve around the Milky Way. There are 20 dwarf galaxies in existence from Segue-1 (the smallest) to Canes Venatici-1 (the largest), and dark matter is only meant to work by spreading out across a wide distance, but it is still used to explain dwarf galaxies, even though this requires dark matter to be concentrated within these systems, which is implausible. "In a study published in Nature, researchers have now looked at six massive, star-forming galaxies from when the universe was around four billion years old. These distant galaxies were observed using the ESO's Very Large Telescope, which allowed researchers to measure the rotation of the galaxies. Their findings were something of a surprise. Unlike the spiral galaxies we see today, the outer regions of the six observed appear to be rotating far slower than the areas close to their centers – a finding that is at odds with simulations of how early galaxies form. It also suggests that there is less dark matter present compared to galaxy we see today. Reinhard Genzel, lead author of the study, explained: "Surprisingly, the rotation velocities are not constant, but decrease further out in the galaxies. There are probably two causes for this. Firstly, most of these early massive galaxies are strongly dominated by normal matter, with dark matter playing a much smaller role than in the Local Universe. Secondly, these early discs were much more turbulent than the spiral galaxies we see in our cosmic neighborhood” (Figure 6).²²

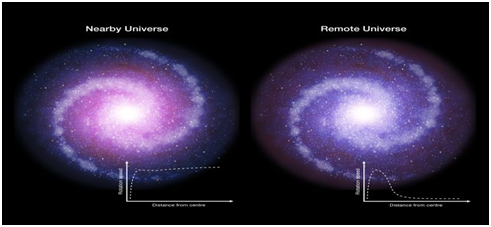
Figure 6 Most early massive galaxies are strongly dominated by normal matter. PR Image eso1709a.¹⁷

The greatest challenge to modified gravity theories, and also the clearest direct evidence of Dark Matter, comes from observations of a pair of colliding galaxy clusters known as the Bullet Cluster in which the stars and Dark Matter separate from the substantial mass of ionized gas. The Dark Matter follows the less substantial stars and not the more massive gas. Since the new bullet cluster is less massive and the merger slower, weighing its dark matter could be harder. The dark matter hypothesis for the bullet cluster is contradicted by the cold dark matter ΛCDM model. The initial relative velocity of the two colliding clusters would need to be around 3000 km/s in order to explain the observed shock velocity, X-ray brightness ratio and morphology of the main and sub-cluster. Jounghun et al.²³ have shown that such a high infall velocity is incompatible with the predictions of the cold dark matter ΛCDM model Figure 7.²⁴ The probability that such an event could occur is roughly one in 10 billion!²³

Figure 7 The Matter of the Bullet Cluster.¹⁷

An alternative to Dark Matter is to explain the missing mass by means of modification of gravity at large distances or more specifically at small accelerations. In 1983, Morderhai Milgrom proposed phenomenological modification of Newton’s law which fits galaxy rotation curves. The theory, known as Modified Newtonian Dynamics (MOND) automatically recovers the Tully-Fischer law. The theory modifies the acceleration of a particle below a small acceleration ${\text{a}}_0={10}^{-10}{\text{ms}}^{-2}$ . This therefore enters the theory as a universal constant. The gravitational acceleration at large distances then read $sa=\sqrt{{\text{GMa}}_0}/\text{r}$  at large distances, instead of the Newtonian $\text{a}=\sqrt{\text{GM}}/\text{r}$.¹ There are two main difficulties with MOND. First, it does not explain how galaxy clusters can be bound without the presence of some hidden mass. Second, attempts to derive MOND from a consistent relativistic field theory have failed. One such attempt is the Tensor-Vector-Scalar. Many models are unstable or require actions which depend on the mass M of the galaxy, thereby giving a different theory for each galaxy. Moreover modified gravity theories have serious difficulties reproducing the CMB power spectrum. Modified gravity theories can give an excellent phenomenological fit through an adjustment of the values of the extra parameters, but there is no universal principle to determine these values. This requirement for simplicity and predictivity is met by General Relativity. The modifications of gravity proposed as alternative to the Dark Matter paradigm illustrate the need for tests of GR at large distances and low accelerations. For the versions of MOND, the basic idea is this: there is no dark matter, but there are two different metrics −metrics are space-times coupled to matter. One metric is coupled to ordinary matter. Gravtitational waves, on the other hand, have an entirely different metric that, is warped out of shape. Its warped shape is what we perceive as dark matter. So there is no dark matter−instead the space-time is naturally warped in the absence of dark matter. These two seemingly independent metrics can explain the structures of galaxies and of collisions between galaxy clusters, but the idea has consequences. For instance, if a something should emit both gravitational waves and light, the two waves will travel by different paths depending on the masses they encounter. So, light and gravitational waves won't arrive at a distant observation point at the same time. When two neutron stars spiraled into each other and merged, they released a huge amount of energy as both light and gravitational waves. The light and the gravitational waves travel along the direct line of sight to us, curling around the gravity wells of intervening galaxies along the way. As a result, the initial burst of light and gravitational waves hid a little gem: the time difference between the arrival of the gravitational waves and the light. All 1.7 seconds of it.²⁵ The measured delay was so much shorter than the difference predicted by double metric theories. Yes, that was the recorded delay between the two signals. This is a dead MOND.²⁶

Hyperbolic space-time and hyperbolic trajectory, not dark matter, resolves the discrepancy between the flat rotation curves of stars within a galaxy and the rotation curves expected from Kepler's third law. The orbital velocity of a body traveling along hyperbolic trajectory in flat space can be computed as Vallado theorem.²⁷

$V=\sqrt{\frac{2\mu }{r}-\frac{\mu }{a}}$           (41)

Where: $\mu$  is standard gravitational parameter, r is radial distance of orbiting body from central body and a is the hyperbola negative semi-major axis.

The orbit of Mercury around the sun doesnt obey Newton's law of gravity that governs the rest of the plant`s orbits. This is due to the curved spacetime near the sun. According to Newton's law of gravity the orbit of Mercury around the sun should be a perfect ellipse with the sun at one focus. That's just Kepler's first law. Mercury was not precisely following its predicted orbit. The sun has the strongest gravitational field of any object in the solar system. Since, according to general relativity the curvature of spacetime is a direct measure of the strength of a gravitational field. As Mercury tries to move along an elliptical orbit, the orbit itself slowly moves. This effect called the precession of Mercury's perihelion. The gravity near the sun is strong enough to warp space-time. Far away from the sun the space-time turns flat, the other planets obey Keplerian elliptical orbit. The same analogy can be applied to describe the trajectory of a galaxy within the hyperbolic space-time of its parent cluster. The hyperbolic space-time causes the galaxy to speed up as moved away from the center. Far away from the center the space-time return flat, while one could apply Vallado theorem for the hyperbolic trajectory in the flat spacetime. The body traveling along hyperbolic trajectory will attain in infinity an orbital velocity called hyperbolic excess velocity  that can be computed as

$V_{\infty }=\sqrt{-\frac{\mu }{a}}$       (42)

Where: $\mu =\text{Gm}$ is standard gravitational parameter and a is the negative semi-major axis of orbit’s hyperbola.

Kepler's third law and consequently Virial theorem does no longer hold for Non-Euclidian space. In the hyperbolic space-time, galaxies furthest away from the center are moving fastest until they reached large distance from the center the space-time return flat. They possessed hyperbolic trajectory, according to Vallado theorem, with constant speed, called hyperbolic excess velocity, ${\text{V}}_{\infty }=\sqrt{-\frac{\text{μ}}{\text{a}}}$  that account for the flat curve.

To seek completeness, it remains to develop an equation of motion describes the speed up motion in the hyperbolic space-time and predicts the flat curve. To do this, I will follow the following strategy

1. Seek for an equation $v=f\left(r\right)$  such that $v=\underset{r\to 0}{\lim }f\left(r\right)=0$
2. $v=f\left(r\right)\stackrel{l\arg e.r}{\to }\sqrt{\mu \left(\frac{2}{r}-\frac{1}{a}\right)}\stackrel{r\to \infty }{\to }\sqrt{-\frac{\mu }{a}}$
3. I guess the required equation –fits the data- should be

 $v=f\left(r\right)=e^{-\frac{1}{r}}\sqrt{\mu \left(\frac{2}{r}-\frac{1}{a}\right)}.$       (43),

1. The final step in the mathematical problem solving method is to prove the conjecture

$v=f\left(r\right)=e^{-\frac{1}{r}}\sqrt{\mu \left(\frac{2}{r}-\frac{1}{a}\right)}.$

To find such an equation of the radial motion in the galaxy`s hyperbolic space-time, we proceed as follows: The required modified Schwarzschild spherically symmetric metric will be

$d{\tau }^2=e^{\nu }d{t}^2-e^{\lambda }d{r}^2-r^{2}d{\Omega }^2$    (44)

$\begin{array}{l}d{\tau }^2=\left(1+\nu +\left(1/2\right){\nu }^2+\mathrm{...}\right)d{t}^2\\ -\left(1+\lambda +\left(1/2\right){\lambda }^2+\mathrm{...}\right)d{r}^2-r^{2}d{\Omega }^2\end{array}$ (45)

For which the Schwarzschild metric is just an approximation

$d{\tau }^2=\left(e^{\nu }\right)d{t}^2-\left(e^{\lambda }\right)d{r}^2-r^{2}d{\Omega }^2$      (46)

$d{\tau }^2\approx \left(1+\nu \right)d{t}^2-\left(1+\lambda \right)d{r}^2-r^{2}d{\Omega }^2$           (47)

The Ricci tensor

$\begin{array}{l}0=R_{tt}=-\left(1/2\right)e^{\nu -\lambda }\left({\nu }^{″}+{{\nu }^{\prime }}^2/2-{\nu }^{\prime }{\lambda }^{\prime }/2+2{\nu }^{\prime }/r\right),\mathrm{...}(i)\\ 0=R_{rr}=\left(1/2\right)\left({\nu }^{″}+{{\nu }^{\prime }}^2/2-{\nu }^{\prime }{\lambda }^{\prime }/2+2{\lambda }^{\prime }/r\right),\mathrm{...}(ii)\\ 0=R_{\theta \theta }=-\left\{1-{\left(e^{-\lambda }r\right)}^{\prime }+e^{-\lambda }r\left(\frac{{\nu }^{\prime }+{\lambda }^{\prime }}{2}\right)\right\},\mathrm{...}(iii)\end{array}$    (48)

From $R_{tt}=R_{\theta \theta }=0$  web have ${\nu }^{\prime }+{\lambda }^{\prime }=0$ ,

So $\nu +\lambda =k$     (49)

K is constant. Write simply $\lambda =-\nu +\log k$ . Equation (i) is now just

${\left(e^{\nu }r\right)}^{{\prime }^{\prime }}=0$     (50)

$e^{\nu }r=-\alpha +\beta r$      (51)

Equation (iii) is

${\left(e^{-\lambda }r\right)}^{\prime }=1$      (52)

${\left(e^{\nu }r\right)}^{\prime }=k$      (53)

$\therefore \beta =k$     (54)

Now we have the complete solution

$e^{\lambda }={\left(1-2\mu /kr\right)}^{-1}\approx {\left(e^{-2\mu /kr}\right)}^{-1}=e^{2\mu /kr}$           (55)

$e^{\nu }=k\left(1-\alpha /kr\right)=k\left(1-2\mu /kr\right)=\left(k-2\mu /r\right)$      (56)

For radial motion, $d{\Omega }^2=0$ . The Schwarzschild metric will be

$d{\tau }^2=e^{\nu }d{t}^2-e^{\lambda }d{r}^2$       (57)

$d{\tau }^2=\left(k-2\mu /r\right)d{t}^2-e^{2\mu /kr}d{r}^2$         (58)

The free fall from rest of a star (of mass m and energy E) far from the center possesses

$\frac{E}{m}=\left(1-\frac{2\mu }{r}\right)\frac{dt}{d\tau }=1$     (59)

${\left(\frac{d\tau }{dt}\right)}^2={\left(1-\frac{2\mu }{r}\right)}^2$        (60)

${\left(\frac{d\tau }{dt}\right)}^2=\left(k-2\mu /r\right)-e^{2\mu /kr}{\left(\frac{dr}{dt}\right)}^2$      (61)

${\left(1-2\mu /r\right)}^2=\left(k-2\mu /r\right)-e^{2\mu /kr}{\left(\frac{dr}{dt}\right)}^2$            (62)

To our purpose for the hyperbolic spacetime, the velocity far away from the center would be $V_{\infty }=\sqrt{-\mu /a}$  and consequently $k=1-\mu /a$

$\left(1-4\mu /r+{\left(2\mu /r\right)}^2\right)=\left(1-2\mu /r-\mu /a\right)-e^{2\mu /\left[\left(1-\mu /a\right)r\right]}{V}^2$      (63)

Neglect the term ${\left(2\mu /r\right)}^2$ and rearrange

$\left(1-4\mu /r\right)=\left(1-2\mu /r-\mu /a\right)-e^{2\mu /\left[\left(1-\mu /a\right)r\right]}{V}^2$          (64)

$e^{2\mu /\left[\left(1-\mu /a\right)r\right]}{V}^2=\left(2\mu /r-\mu /a\right)$           (65)

$V=e^{-\mu /\left[\left(1-\mu /a\right)r\right]}\sqrt{2\mu /r-\mu /a}$      (66)

$V=e^{-a\mu /\left[\left(a-\mu \right)r\right]}\sqrt{2\mu /r-\mu /a}$ $V=e^{-a\mu /\left[\left(a-\mu \right)r\right]}\sqrt{2\mu /r-\mu /a}$    (67)

$\begin{array}{l}\because -a>>\mu \\ \therefore a-\mu \approx a\end{array}$      (68)

$\left(1-\mu /a\right)\left(km/s\right)\approx 1\left(km/s\right)$      (69)

$V=e^{-\mu /r}\sqrt{2\mu /r-\mu /a}$    (70)

Example 1

A typical galaxy of ordinary enclosed mass (e.g. Milky Way or Andromeda) where $M_{\odot }$  is the mass of the sun:²⁸

$M={10}^{11}{M}_{\odot }={10}^{11}\times 2\times {10}^{30}kg$     (71)

$\mu ={10}^{11}\times 2\times {10}^{30}\times 7.4\times {10}^{-31}km$      (72)

$\mu =1.5\times {10}^{11}km$            (73)

$\mu =1.5\times {10}^{11}km\times \left(s/s\right)$       (74)

$\mu =1.5\times {10}^{11}km\times \left(3\times {10}^{5}km/s\right)$      (75)

$\mu =4.5\times {10}^{16}\left(k{m}^2/s\right)$            (76)

$210=\sqrt{\mu /-a}$       (77)

${\left(210\right)}^2=\mu /-a$              (78)

$V=e^{\mu /r\left(kpc\right)}\sqrt{2\mu /r\left(kpc\right)-\mu /a}$     (79)

$\begin{array}{l}V=e^{-4.5\times {10}^{16}\left(k{m}^2/s\right)/\left(1\left(km/s\right)\times r\left(3.1\times {10}^{16}km\right)\right)}\times \\ \sqrt{{}^{9\times {10}^{16}\left(k{m}^2/s\right)/\left(1\left(km/s\right)\times r\left(3.1\times {10}^{16}km\right)\right)+{210}^2}}\end{array}$          (80)

$V=e^{-1.45}\sqrt{{}^{2.9/r+{210}^2}}$        (81)

The curve of this equation by visual math program as follows (Figure 8)

Figure 8 The curve describes the motion of a star in the Milky Way (or Andromeda) galaxy. The vertical axis represents the velocity, while the horizontal axis represents the distance from the center of the galaxy.

Example 2

A typical cluster of galaxies of ordinary enclosed mass

$M={10}^{14}{M}_{\odot }={10}^{14}\times 2\times {10}^{30}kg$     (82)

$\mu ={10}^{14}\times 2\times {10}^{30}\times 7.4\times {10}^{-31}km$     (83)

$\mu =1.5\times {10}^{14}km$           (84)

$\mu =1.5\times {10}^{14}km\times \left(3\times {10}^{5}km/s\right)$        (85)

$\mu =4.5\times {10}^{19}\left(k{m}^2/s\right)$         (86)

$1000=\sqrt{\mu /-a}$        (87)

${\left(1000\right)}^2=\mu /-a$      (88)

$V=e^{-\mu /(r{\rm M}pc)}\sqrt{2\mu /r(10{\rm M}pc)-\mu /a}$    (89)

$V=e^{-4.5\times {10}^{19}/\left(3.1\times {10}^{19}\times r\right)}\sqrt{2\times 4.5\times {10}^{19}/\left(3.1\times {10}^{19}\times r\right)+{\left(1000\right)}^2}$            (90)

$V=e^{-1.45/r}\sqrt{2.9/r+{\left(1000\right)}^2}$      (91)

The curve of this equation by visual math program as follows (Figure 9):

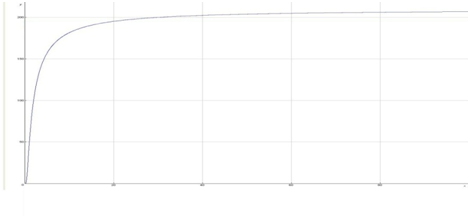
Figure 9 The curve describes the motion of a cluster of galaxies. The vertical axis represents the velocity, while the horizontal axis represents the distance from the center of the cluster.

The dark matter halo is nothing but instead of it we have a cell of same hyperbolic negative curvature as the negative curvature of the whole Hyperbolic Universe. Virial theorem $\text{V}=\sqrt{\frac{\text{MG}}{\text{r}}}$  does no longer hold for Non-Euclidian space. We developed the equation of motion in the hyperbolic spacetime: $\text{V}={\text{e}}^{-\text{μ}/\text{r}}\sqrt{\text{μ}\left(2/\text{r}-1/\text{a}\right)}$ , that describes the speed up motion in the hyperbolic space-time and predicts the flat curve. Farther away from the center the exponential factor ${\text{e}}^{\frac{-1}{\text{r}}}$  drops to one. Galaxies furthest away from the center are moving fastest until they reached large distance from the center the space-time turns flat and they possessed hyperbolic trajectory: $\text{V}=\sqrt{\text{μ}\left(2/\text{r}-1/\text{a}\right)}$  , according to Vallado theorem, with constant speed called hyperbolic excess velocity: ${\text{V}}_{\infty }=\sqrt{-\frac{\text{μ}}{\text{a}}}$  that can account for the galaxy flat rotation curve problem, a is the negative semi-major axis of orbit's hyperbola.

Newton's laws of gravity is valid only in an Euclidean space. Newton's laws of gravity do no longer hold in the large structure non-Euclidean geometry. Any attempt to modify Newton's laws of gravity (e.g. MOND) would not help, for it didn't take into account the relativistic physics of the large structure. For large structure scale and cosmological scale the curvature of the spacetime would no longer be ignored, where General Relativity dominated. We neither need a new theory for gravity nor modify the General Relativity Theory. We need to overcome the shortcoming of the General Relativity Theory at extreme scales. Such a shortcoming is a consequence of the approximations and the oversimplification assumptions made to simplify Einstein's Field Equations in order to solve the associated Friedmann's differential equations. The pressureless–dust flat universe model is an oversimplification solution to the Einstein's Field equations. This led to a drastic failure in predicting the missing mass and the accelerating expansion of the universe. Our main failure is that we accept an unverifiable assumption that the portion of the universe which can be observed (which is flat) is representative of the whole (which is curved), and that the laws of physics are the same throughout the whole universe. It is an oversimplification to generalize that the universe is globally flat and the laws of physics are the same throughout the globe universe. In General Relativity Theory, gravity is geometry. In order to modify the laws of gravity, a natural first step is to modify the geometry itself. Hence, we establish the modified laws of gravity from the updated non-Euclidean geometry. We prove that the topology of the universe globally is hyperbolic. We develop the laws of gravity in the hyperbolic space time. Such laws fit the current observed data and ruling out both dark matter and dark energy. Hence, the universe is not dark.

According to Occam's razor the model should be aesthetically pleasing, that is "If you have two theories that both explain the observed facts, then you should use the simplest with the fewest assumptions. We compare between the Flat Universe paradigm and the Hyperbolic Universe paradigm via the Table 2. The Hyperbolic Universe is aesthetically pleasing since it satisfies the Occam's razor.

None.

1. Debono I, Smoot GF. General Relativity and Cosmology: Unsolved Questions and Future Directions. Universe. 2016;2(4):23.
2. E Lerner. An Open Letter to the Scientific Community. A Cosmology Group. 2004.
3. Mabkhout SA. The Big Bang Universe Neither Needs Inflation Nor Dark Matter and Dark Energy. Phys Essays. 2013;26(3):422.
4. Mabkhout SA. The Hyperbolic Geometry of the Universe and the Wedding of General Relativity Theory to Quantum Theory. Phys Essays. 2012;25:112.
5. S Perlmutter, G Aldering, Goldhaber, et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. The Astrophysical Journal. 1999;517(2):565.
6. Charles Baltay. The accelerating universe and dark energy. International Journal of Modern Physics. 2014;23(6):1430012.
7. Riess AG, Filippenko AV, Challis P, et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal. 1998;116:1009.
8. Dennis Overbye. In the Beginning. USA: The New York Times. 2002 .
9. High Z Supernova Search. Team, HST, NASA.
10. Low Density Inflationary Universes. Stuart Levy of the University of Illinois, Urbana-Champaign and Tamara Munzer of Stanford University.
11. LIGO Scientific Collaboration. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. The Astrophysical Journal Letters. 2017;848(2):27.
12. David Polarski. Dark energy. Int J Mod Phys D. 2013;22(14):1330027.
13. Sibel Boran, Shantanu Desai, Emre Kahya, et al. GW170817 Falsifies Dark Matter Emulators. Phys Rev D. 2018;97:041501.
14. James B Hartle. Gravity An Introduction To Einstein's General Relativity. San Francisco: Addison Wesley; 2003. p. 582.
15. Geometry of the universe.
16. A Einstein. The Meaning of Relativity. New Jersey: Princeton University Press; 2005. p. 117−118.
17. A Review of the Universe - Structures, Evolutions, Observations, and Theories.
18. Dark Matter.
19. Vera Rubin Didn't Discover Dark Matter. 2016.
20. E Aprile. First Dark Matter Search Results from the XENON1T Experiment. 2017;119:181301.
21. Xiangyi Cui. Dark Matter Results from 54-Ton-Day Exposure of PandaX-II Experiment. 2017;119:181302.
22. Timothy D. Brandt, Constraints on MACHO Dark Matter from Compact Stellar Systems in Ultra-Faint Dwarf Galaxies. The Astrophysical Journal Letters. 2016;824(2):1−5.
23. Reinhard Genzel. VLT observations of distant galaxies suggest they were dominated by normal matter. Dark Matter Less Influential in Galaxies in Early Universe. Release no: eso 1709.
24. Jounghun L, Eiichiro K. Bullet Cluster: A Challenge to LCDM Cosmology. The Astrophysical Journal. 2010;718(1):60.
25. Maxim Markevitch. Chandra observation of the most interesting cluster in the Universe. 2005.
26. Hyperbolic trajectory.
27. Eric Chaisson, Steve McMillan. Astronomy Today. 6th ed. USA: Addison Wesley; 2008. p. 636.