We put the question, how gravitational fields are communicated to space, and how they are recognized in space by moving objects. The general answer given to this question in these days is that field quanta of the gravitational field, called gravitons, are responsible for the communication of such fields. This answer is taken serious here, and then consequently is put into serious doubts when studying several physically coherent consequences.  We start by investigating the gravitational influence of cosmic mass associations on moving massive objects when hereby the effect of propagating gravity field quanta, i.e. the gravitons, communicating the position of gravity sources, is taken into account. It is shown that moving objects are affected by gravity sources from a relativistically displaced position, like stars are seen under an aberration angle compared to the true source position. The astonishing effect of that mislocation is that a moving object at its passage through the center of a centrally symmetric galactic mass association undergoes a permanent gravitational deceleration of its relative motion. Furtheron it is shown that under this new view the problem of a planetary object, orbiting a central mass like the sun, takes a non-Keplerian solution, because the orbiting planet permanently should lose orbital angular momentum, since it permanently experiences a gravitational force component antiparallel to its orbital motion. From that an orbital decay time can be derived which predicts that a terrestrial planet should have a spiralling-in period of only a few ${10}^4$  years which, compared to the expected age of the Earth of about $4.5$  Billion years, represents a big problem of understanding. In addition, in view of the presumed action of gravitons from an aberrated source position, this article studies the propagation of cosmic photons over the photospheric limbs of stars. We show that when the center of the gravity field acts from a relativistically displaced position, then no energy change of limb photons when again propagating to larger distances should occur - which does confirm Einstein‘s view - , but also no deflection from the original propagation direction of the photon should occur - which contradicts Einstein‘s derivations. In this article we do not yet offer a rational solution of these newly pinpointed problems, but we simply end with the recommendation to perhaps reinvestigate the theoretical concept of gravitons, thought as to be the quantum messengers of gravitational fields.

Since investigations of the English astronomer James Bradley (1728) it has become general astronomical standard knowledge that the apparent position at which stars appear at the sky for an observer at earth depends on the phase of the year. Followed over the whole year, the position varies along ellipses on the sky. Quickly after this finding it became clear that the position of the respective star varies with the orbital velocity $\begin{array}{l} \hfill \\ \hfill \end{array}\overrightarrow{U}$  of the earth which serves as the moving platform in space from where astronomers observe the stellar constellations. Since the orbital velocity $\begin{array}{l} \hfill \\ \hfill \end{array}\overrightarrow{U}$  of the earth has an annual periodicity, the apparent positions of stars at the sky show this same periodicity with the vector of the earths orbital velocity around the sun. This general aberration phenomenon of "fix"- stars could well be understood as consequence of Michelson-Morley‘s epoch making prove that the propagation velocity of light is finite and amounts to $c=300000km/s$ .¹ The light arriving from the star comes into the astromomer‘s telescope focus from a slightly variable direction dependend on the actual velocity $\overrightarrow{U}=\overrightarrow{U}\left(t\right)$  of the earth. This classic aberration phenomenon is well known amongst astronomers since James Bradley (1728) and nowadays taken as a solid fact.

Now an urgent consequent and subsequent question may be provocated concerning the analogous mis-location of gravitational cosmic sources, instead of electromagnetic sources. Of course, stellar gravity fields are not radiation fields in the usual sense, rather they may in general appear as constant source-related fields in space. But one should keep in mind that according to modern physical understandings gravity fields are quantum fields, just like electromagnetic fields. The location of the sources of cosmic gravity fields thus is communicated to cosmic space by the outflow of gravitons as the quanta of this fields. Since, however, these gravitons according to our present understanding have a limited propagation velocity equal to that of light , i.e. $c_g=c_{el}=c$ , an aberration effect similar to that of radiating stars should also cause that the centers of stellar gravity appear dislocated from their true positions, dependend on the velocity $\overrightarrow{U}$  of the gravity sensors. In this respect "gravity sensors" are represented by massive objects, particles or photons reacting to cosmic gravity fields. That idea should allow to conclude that centers of stellar gravity fields consequently influence and affect moving objects, particles or photons from an apparently aberrated position. In the following we shall briefly investigate related effects and consequences of such "gravitational aberrations" in sections 2. to 4. , and then in section 5. look for conclusions which should be drawn from this challenging new view.

The cosmic deceleration of moving objects at crossings of galaxy clusters

Recently it has been investigated how massive, cosmic objects are affected, when moving along their trajectories with a peculiar velocity $\overrightarrow{U}$  through the gravitational fields of the ambient masses of the universe and do see the positions of discrete cosmic mass sources like stars, galaxies or galaxy clusters relativistically displaced with respect to their real positions given in the cosmic rest frame.^2,3 This "gravitational aberration" phenomenon, well known amongst astronomers by its electromagnetic analogue as "stellar aberration", should have most interesting, surprising effects on the gravitationally influenced motion of such objects.

The above mentioned authors considered the situation that the locations of the sources of gravity, due to the finite propagation velocity $v_g=c$  of gravitons, are recognized or perceived by gravitationally influenced moving particles or photons at "relativistically retarded" positions. Hence the apparent direction of the gravitational pull with respect to the location of the real mass source experiences an aberration, meaning that it appears as displaced by a certain angle$\delta \theta$ . If a corresponding mass element $\delta M_C$  on a spherical mass shell of a cluster at a radial distance $r$  is "gravitationally" seen by an object at rest with respect to the cluster center under an angle $\theta$ , it instead acts upon a moving particle or photon effectively not from this direction $\theta$ , but from an apparently different direction $\theta `=\theta +\delta \theta$ , when viewed by the moving particle with velocity $\overrightarrow{U}=U$  $\overrightarrow{k}$  or by the photon with a velocity $\overrightarrow{c}=c$  $\overrightarrow{k}$ .

According to SRT- relations these two angles $\theta$  and ${\theta }^{\text{'}}$  for an object moving with a velocity $\begin{array}{l} \hfill \\ \hfill \end{array}\overrightarrow{U}=U\overrightarrow{k}$  are connected by the following relation:⁴

$\text{cos}{\theta }^{\text{'}}=\frac{cos\theta +\beta }{1+\beta cos\theta }$   (1)

where $\beta$  is given by $\beta =U/c$ . Imagining now an object at a distance $R$  from the center of a cluster (see Figure 1 for illustration), then it is evident that this object is attracted by the gravitation of a mass element $\delta M_C$  under an angle ${\theta }^{\text{'}}$  given by the formula above, when this mass element , judged from the rest frame of the cluster, is located under an angle $\theta$ .

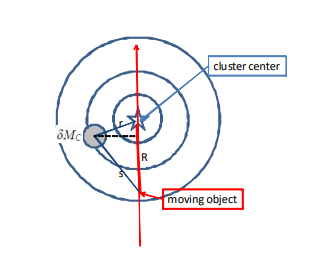
Figure 1 Illustration of a moving object crossing a radially symmetric cluster mass system.

This, however, means that along the trajectory an effective, attractive force acts given by

$\overrightarrow{k}\cdot \delta \overrightarrow{K}=-G\delta M_C\frac{\text{cos}{\theta }^{\text{'}}}{R{\text{'}}^2+r^2+2rR\text{cos}\theta }$   (2)

which lead to unexpected new effects.

One can easily agree to the point that forces perpendicular to $\overrightarrow{k}$  cancel as long as the object is moving on a central line crossing right through the center of the spherically symmetric mass cluster at $r=r_c=0$ . But calculating now the integrated forces $\overrightarrow{K}$  in direction $\overrightarrow{K}$   of the motion, acting on the moving object at the place $R$  , one obtains the following, surprising result^2,3 when assuming spherically symmetric mass distribution according to $\begin{array}{l} \hfill \\ \hfill \end{array} \rho \left(r\right)={\rho }_{C,0}\text{exp}\left[-r/r_0\right]$ :

$K=-G\pi {\rho }_{c,0}\int \theta \int r\exp \left[-\frac{r}{r_o}\right]\sin \theta d\theta \frac{\frac{\cos \theta +\beta }{1+\beta \cos \theta }}{R^2+r^2+2rR\cos \theta }{r}^{2}dr$   (3)

For the case $R=0$ , i.e. the object is located just in the center of the cluster, this expression is simplified to the following, easily handable expression:

$K=-G\pi {\rho }_{c,0}{\int }_0^{\infty }\exp \left[-\frac{r}{r_o}\right]dr\cdot {\int }_0^{\pi }\frac{\cos \theta +\beta }{1+\beta \cos \theta }\sin \theta d\theta$   (4)

making evident that even in the cluster center at $R=0$ , being surrounded by a spherically symmetric mass distribution of the cluster, the moving object experiences a net force given by the following evaluated expression:

$K=-G\pi {\rho }_{c,0}{r}_0{\int }_0^{\pi }\frac{\cos \theta +\beta }{1+\beta \cos \theta }\sin \theta d\theta =-\frac{3}{4}G\frac{M_c}{r_0^2}\left[\frac{1-{\beta }^2}{{\beta }^2}In\left[\frac{1+\beta }{1-\beta }\right]-\frac{2}{\beta }\right]$   (5)

where $M_C$  denotes the total mass of the cluster. In Figure 2 the force $K\left(\beta \right)$  is shown as function of $\beta =U/c$  making it also evident that for $U=\beta =0$  this force $K\left(\beta =0\right)$  vanishes.

Figure 2 The force $K\left(\beta \right)$ normalized by $[3G{M}_C/4r_0^2]$ is shown as function of $\beta =U/c$ .

The above result at first glance appears counter-intuitive, since, as is generally known, in the center of a symmetric mass distribution one would normally not expect any net gravitational force, i.e. in the center of the Sun or the Earth there is no gravitational force. In case, however, when the object in the center is moving with velocity $U$ , then in fact there is a net acting force given by the upper expression. Only for the case of $\beta =U=0$   there exists no force. Also the general scientific wisdom, that inside a spherical mass shell no gravitational field is felt, obviously does not hold for an object in motion with $\beta \ge 0$ . This is because a moving object recognizes the surrounding single mass elements on the spherical shell at asymetrically displaced positions, and hence no spherical gravitational symmetry is valid for this object. This appears surprising and we may keep this result in mind as a challenge for our further investigations.

Aberration of the gravity source for the moving object at Keplerian motions

Regarding the relativistic dislocation of a planetary object orbiting the central gravity source, the Sun, in a quasicircular orbit, it is interesting to pay attention to the already pronounced difference between the situation $A:$  in the Suns rest frame, and $B:$  in the frame of the moving planetary object.  In the Suns rest frame the object moving in a circular orbit around the sun, at its actual position with respect to the direction of its circular motion $\overrightarrow{U}$ , sees the center of gravity, i.e. the sun, at an angle $\theta =\pi /2$  or $\text{cos}\theta =0$ .  In its own rest frame moving with $\overrightarrow{U}$ , however, the object recognizes the gravity center at an angle ${\theta }^{\text{'}}$  which latter as already presented in the section ahead depends on $\beta =U/c.$ This means that instead of seeing the center of gravitation from the moving planet under the angle $\theta ={90}^{\circ }$ , under these prerequisites it sees it under the angle ${90}^{\circ }+\delta \theta$ , with $\delta \theta =-U/c$  (see Equ. (??)) which implies that there permanently exists a gravitational force component acting on the moving planet at its circular motion antiparallel to its orbital velocity $\overrightarrow{U}$  .

Hence evidently this force tends to reduce the orbital velocity $U$  by the following amount

$m\frac{d\overrightarrow{U}}{dt}=-\text{cos}\theta \frac{Gm{M}_s}{R^2}$   (6)

consequently causing a decrease of the orbital velocity $U$  and leading to the following first-order equation of motion under the action of the first-order perturbation force $K_{\parallel }=-\left(U/c\right)K$  :

$\frac{d\overrightarrow{U}}{dt}=-\frac{U}{c}\frac{G{M}_s}{R^2}$   (7)

or with introduction of the orbital period of the Earth around the Sun with $\begin{array}{l} \hfill \\ \hfill \end{array}{Y}_E=2\pi R_E/U_E=1$   leading to:

$U\left(t\right)=U_E\text{exp}\left[-\frac{c}{U_E}\frac{2\pi G{M}_s}{c^2{R}_E}\frac{\left(t-t_0\right)}{Y_E}\right]$   (8)

With the Schwartzschildradius of the sun, $r_{SS}=(2G{M}_s)/c^2$  , this thus leads to:

$U\left(t\right)=U_E\text{exp}\left[-\frac{c}{U_E}\frac{\pi r_{SS}}{R_E}\frac{\left(t-t_0\right)}{Y_E}\right]$   (9)

This formula tells us that a typical relativistic decay period of the quasi-circular spiralling-in orbital motion of e.g. the Earth is given by about a period of ${\tau }_E=\left(U_E/c\right)\left(R_E/\pi r_{SS}\right)\simeq 1.6\cdot {10}^3{Y}_E$  and does indicate the very astonishing result that circumsolar orbits at distances smaller than or equal to $R=R_E$  should have a decay period of only a few thousand years. How under these circumstances the solar system and its planets could have reached an age of 4.5 Billion years? - That represents another challenge to this theory of relativistically mislocated gravity sources.

Propagation of cosmic photons over stellar limbs

Challenged by the above results, we now shall study the effect of how, in view of the new auspices mentioned in this present article here, a central gravity source like a star should influence a photon propagating on a straight line just passing over the limb of the stellar photosphere of this star. As elaborated in detail by Fahr²¹ a photon with the energy $E_{\nu }=h\nu$  passing along the $x$ -axis over the limb $y=r_s$  of a star will undergo an energy change per increment $dx$  on the $x$ -axis (for an illustrative view see Figure 3) given by:

Figure 3 Propagation of a photon just over the limb of a stellar photosphere.

$d\left(h\nu \right)=-dx\frac{h\nu }{c^2}\frac{GM}{\left[x^2+y^2\right]}\text{cos}{\vartheta }^{\text{'}}$   (10)

where in this case the relativistically relevant angle ${\vartheta }^{\text{'}}$ , associated with the real position angle $\vartheta$ , for the photon with ß $=U/c=1$  is given by:

$cos\vartheta `=\frac{\text{cos}\vartheta +1}{1+\text{cos}\vartheta }=\pm 1$   (11)

while (see Figure 3) in the stellar rest frame the position angle $\vartheta$  is given by $\begin{array}{l} \hfill \\ \hfill \end{array}cos\vartheta =x/\sqrt{x^2+y^2}$ .

Consequently at the propagation of a photon from $x=-\infty$  to $x$ , in view of the physical work done by the photon, the photon frequency $v(x)$  changes as given by the following relation:

$\nu \left(x\right)={\nu }_{\infty }\text{exp}\left[-\frac{1}{c^2}\underset{-\infty }{\overset{x}{{\displaystyle \int }}}dx\frac{GM}{x^2+y^2}\text{cos}\vartheta `\right]$   (12)

Here $G$  is the gravitational constant, and $M$  is the stellar mass. For a photon propagating from $x=-\infty$  to $x=+\infty$  one, when inserting $\text{cos}{\vartheta }^{\text{'}}=\pm 1$ , the following frequency change:

$\nu \left(-\infty ,+\infty \right)={\nu }_{\infty }\cdot \text{exp}\left[-\frac{1}{c^2}\underset{-\infty }{\overset{x=0}{{\displaystyle \int }}}dx\frac{GM}{x^2+y^2}+\frac{1}{c^2}\underset{x=0}{\overset{+\infty }{{\displaystyle \int }}}dx\frac{GM}{x^2+y^2}\right]={\nu }_{\infty }$   (13)

namely no! change of the photon frequency occurs, as already obtained by Einstein⁶ or later by Sexl and Sexl.^7,8

But opposite to Einstein‘s result we now find that under the new auspices of a mis-location of the gravity source one obtains (see Fahr⁵) that the photon at such a limb passage also remains undeflected from its original $x-$ axis due to the permanent vanishing of force components perpendicular to this axis along the whole $x-$ axis , proven by the expression:

$K_{\perp }\left(h\nu ,x\right)=-\frac{h\nu }{c^2}\frac{GM}{x^2+y^2}\frac{\sqrt{1-{\text{cos}}^2\vartheta +{\text{cos}}^2\vartheta -1}}{1+\text{cos}\vartheta }=0$   (14)

This is in opposition to Einstein‘s findings that a deflection of the photon by an angle $\delta =2GM/y{c}^2$  $=R_s/y$  should occur with $R_S$  denoting the Schwarzschild radius of the star with mass $M$ .

In this article we have made use of the standpoint justified by Fahr and Heyl^2,3,9,10 that - not only electromagnetic radiation sources -, but as well gravitational sources in space seen from moving objects, like massive particles in motion or propagating photons, should appear at aberrated, dis-located positions. This gravitational source aberration should evidently occur - just like in the analogous electromagnetic case (see: stellar aberration, James Bradley, 1728) - as long as gravitational fields are communicated to space by gravitons, analogous to electromagnetic radiation fields by electromagnetic photons, and as long as both field quanta propagate with the same velocity $c=c_g=c_e$ , as is the physical knowledge of our present epoch. Based on this knowledge one has to expect aberrations in the recognition of gravitational source positions by moving massive objects or photons as already discussed by the above mentioned authors.

In this article here it is shown that due to this relativistic mis-location of a gravitational source, e.g. like a star, aberrational effects should occur in many important cases when photons or massive particles move over extended distances in cosmic space being influenced by cosmic masses, or scratch closely over photospheric limbs of surrounding stars. As we have shown (see section 4) in the latter case the photon, due to this aberrational effect, will not change its energy at such a limb passage, however, due to this aberrational effect at the same time will also always see the center of the stellar gravity field displaced in such a way that no force component perpendicular to its passage line appears. This means the photon should pass the star undeflected, which would be in contrast to Einstein‘s prediction of a deflection angle by $\delta =2GM/r_s{c}^2$  and to observations made by Fomalont.^11,12 Also the lensing effects observed at recent times by astronomers at stars appearing for us behind a massive foreground galaxy need to be newly interpreted in the light of this new view. We are waiting impatiently for a timely solution of this embarrassing scientific situation.

Especially the general, cosmic "deceleration effect" presented in section 2 needs to be understood, i.e. the effect that peculiar velocities of massive objects are permanently reduced in magnitude at the progress of cosmic time, and the analogue effect onto cosmic photons that they are permanently increasing their redshifts, the longer they propagate through the universe. These effects are most surprising in all their indicated consequences and have encouraged us here in this paper to apply these relativistic gravitational aberration effects in ambient cosmic gravity fields also now to more local and smaller-scaled motions like those of objects and photons through the gravity fields of galaxy clusters or even to Keplerian motions of planetary bodies orbiting their parent central stars. And again at these new applications the results which we derive here are highly surprising, shocking and still looking for observational confirmations and interpretations.

In this paper here we are not presenting a very conclusive result, but we are essentially only raising questions putting the finger on something unexplained and want to excite other scientists from the astronomical community to follow us in these thinkings. Maybe in view of these results we are going so far as to say that the physics and doctrine of gravitons - thought to be the light-fast messengers of gravitational fields - has to be newly conceived.

Even though the theory of a Keplerian object under relativistic gravity effects of the Sun presented in section 4 was simplified in many theoretical respects, the shocking result implying orbital decay times of terrestrial planets of only a few ${10}^3$  years nevertheless is fairly solid and unavoidable. The presented calculation had assumed a planetary orbit which at its loss of orbital angular momentum stays quasicircular over the whole decay period. This of course is not exactly true, but the permanent loss of angular momentum of the planetary object under the given conditions would turn the circular into an elliptical orbit, and a more reliable numerical calculation should be carried out, however, as can easily be proven, would not change the decay time period by an order of magnitude.

At the end of this article this means we do in fact at this moment not see any rational explanation for the very short orbital decay time periods of planets under this special-relativistic gravitational action of the Sun. What kind of a solution of these indicated problems could be imagined? Perhaps the whole concept of gravitational fields being propagated to other gravitationally attracted massive bodies derived in a linearized version of the GRT field equations by Einstein¹³ or later e.g. by Goenner¹⁴ must become again a subject of reinvestigations. Perhaps one must finally even dare to presume that there are in fact no gravitons, and that gravity fields in fact are no quantum fields, even though their existence since long ago,¹⁵ has been claimed for - or these gravitons are perhaps faster than light, gradually removing the presented challenge with $c_g⋗c$ .

At least since up to now there has been no success in the attempt to quantize gravity fields, i.e. Einstein‘s General Relativistic gravity fields, it must be allowed to also hesitate believing in the up to now given concept of gravitons as the quantum bosons of gravitational fields, expected as mass-less and with spin "2". It is perhaps an error to believe that with the recently installed big gravity wave antennas the existence of gravitons had been clearly verified. Maybe gravitational waves have been proven to exist with LIGO- or Virgo-,^16,17 but gravitons up to the present have not been confirmed with these antenna devices.¹⁸ But if in fact gravitational fields are no quantum fields, then one also might find therein the evident solution of the above presented "orbit decay problem".

1. Michelson AA, Morley EW. American Journal of Science. 1887;34:333.
2. Fahr HJ, Heyl M. A universe with constant expansion rate abolishes the need for vacuum energy. Physics & Astronomy Intern Journal. 2020a;4(4):156‒163.
3. Fahr HJ, Heyl M. Redshifting cosmic photons in a non‒expanding universe, Advances in Theoret. & Computat. Physics. 2020b;3(3):220‒227.
4. French AP. In: Special Relativity, Massachusetts Institute of Technology, 1968.
5. Fahr HJ. Passage of cosmic photons over stellar limbs. Advances in Theoret and Computational Physics. 2021;4(4):301.
6. Einstein A. Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. Annalen der Physik. 1911;35.
7. Sexl R, Schmidt HK. Braunschweig/Wiesbaden. 1979.
8. Sexl R, Sexl H. Weisse Zwerge ‒ Schwarze Löcher, Vieweg Verlag. Braunschweig. 1979.
9. Fahr HJ, Heyl M. Stellar matter distribution with scale‒invariant hierarchical structuring. Physics & Astronomy Intern Journal. 2019;3(4):146‒150.
10. Fahr HJ, Heyl M. Energy change of particles and photons at crossing gravity fields of galaxy clusters or single stars: The concept of gravitatons. Advances in Theoretical & Computational Physics. 2020a;3(4):239‒242.
11. Fomalont EB, Sramek RA. Measurement of the solar gravitational deflection of radiowaves in agreement with general relativity. Phys Rev Lett. 1976;36:1475‒1478.
12. Fomalont EB. The deflection of radiowaves by the Sun. Comments in Astrophysics. 1977;7:19‒33.
13. Einstein A. Näherungsweise Integration der linearisierten Feldgleichungen der Gravitation, Sitzungsberichte d. Preuß. Akad. Wiss., Berlin, Math. Nat. Kl. 1916;688‒696.
14. Goenner, H. Einführung in die spez. und allgem. Relativitätstheorie, Spektrum Akad. Verlag, Heidelberg‒Berlin‒Oxford, 1996, pp. 325‒350.
15. Davies PCW. The search for gravity waves, Cambridge University Press, 1980.
16. Abbott BP. Observation of gravitational waves from a binary black hole merger. Physical Rev Letters. 2016;116(6).
17. Castelvecchi D, Witze W. Einstein‘s gravitational waves found at last. NATURE NEWS 11. 2016.
18. Dyson F. Is a graviton detectable?, Int Journal of Modern Physics A. 2013;25.