Gluon jets evolution in the quest for new physics

doi:10.15406/paij.2023.07.00293

eISSN: 2576-4543

Physics & Astronomy International Journal

Review Article Volume 7 Issue 2

Gluon jets evolution in the quest for new physics

Katongo Judith, Davy Kabuswa Manyika

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Mulungushi University, School of Natural and Applied Science, Department of physics, Zambia

Correspondence: Davy Kabuswa Manyika, Mulungushi University, School of Natural and Applied Science, Department of physics, Zambia

Received: April 08, 2023 | Published: May 5, 2023

Citation: Judith K, Manyika DK. Gluon jets evolution in the quest for new physics. Phys Astron Int J. 2023;7(2):109-111. DOI: 10.15406/paij.2023.07.00293

Download PDF

Abstract

In this paper, our task is to review the evolution of Gluon Jets in view of the quest for physics beyond the Standard Model (SM) – the so called New Physics (NP). One of the major goals of the Large Hadron Collider (LHC) is to understand a new mode of matter called the Quark Gluon Plasma (QGP). This seemingly new form of matter consists of a confinement of quarks and gluons observed at very high temperature and density. This paper focuses on heavy ion collisions in order to get an understanding of the interaction of high momentum partons. It is these highly sophisticated interactions that probe quantum chromodynamics theorem at very high temperatures and densities. This results in the QGP phase of NP via propagation of very energetic Gluon Jets.

Keywords: Gluon jets, new physics, heavy ion collisions.

Introduction

From the time Gluon Jets were discovered, their evolution has sparked a lot of interest forcing physicists to study their nature in the quest to understand physics beyond the SM.¹ In simple terms, jets can be viewed as narrowly rays of light or particles made accurately parallel to each other. Due to heavy ion collisions in high energy physics, jets are generated as final stated particles. This phenomenon is realized when a system of quarks and gluons is bombarded with high energy.² Let us now break down this phenomenon into simpler terms for our better understanding. When energy exceeding the quark mass energy is added to this system of quarks and gluons, the quarks tend to ‘repel’ each other resulting in the gluons stretching further.³ This change in energy can be mathematically be described as

$Δ E = 2 m_{q} c^{2}$ (1)

As more and more energy is added to the system, the gluon strings snap resulting in the excess energy being converted into other pairs of quarks whose magnitude cannot be observed by an electronic microscope.⁴ Here what we observe is a spray like or spark of particles (hadronic particles) which have come to be known as jets. In this paper, we shall trim our focus only on gluon jets despite the Quantum Chromodynamics (QCD) jets coming in different varieties. Since there first observation, gluon jets have been a subject of interest despite physicists failing to interpret theoretically the physical meaning of their internal properties.⁵ In the quest for the above information, experiments rely on jet algorithms to isolate gluon jets from other events.

QCD lagrangian and gluon jets evolution

The QCD Lagrangian from Yang-Mills theory can be described as

$L_{Q C D} (ψ_{a}, A) = {\sum \bar{ψ}}_{a} (i γ^{μ} D_{μ} - m_{a}) ψ_{a} - \frac{1}{4} F_{a η ν} F_{a}^{μ ν}$ (2)

Where $ψ_{a}$ are interacting fields, A is the gluon field and D is the covariant derivative given by

$D_{μ} = \partial_{μ} + i g_{s} A_{μ}^{a} t^{a}$ (3)

with the gluon field taking the indices values of $a = 1, ..., N_{c}^{2} - 1 = 8$ .

Further more, here we note that the generators take the form

$t^{a} = \frac{1}{2} λ^{a}$ , $T r [t^{a} t^{b}] = T_{F} δ^{a b}$ , $T_{F} = 1 / 2$ , $[t^{a} t^{b}] = i F^{a b c} t^{c}$ (4)

Thus, the dependence of the strength sensor on the gluon field is given by

$F_{μ ν} = \partial_{μ} A_{ν} - \partial_{ν} A_{μ} - g_{s} F^{a b c} (A_{μ}, A_{ν})$ (5)

From Equation 5, the bare coupling constant for the field strength is given by

$g_{s} = \sqrt{4 π α_{s}}$ (6)

Rewriting Equation 6 give us

$α_{s} = \frac{g_{s}^{2}}{4 π}$ (7)

where the QCD running coupling constant is momentum dependent. By combining Equations 6 and 7 and using the energy squared scale we finally obtain

$α_{s} (Q^{2}) = \frac{α_{s} (μ^{2})}{1 + B α_{s} (μ^{2}) I n (\frac{g^{2}}{μ^{2}})}$ (8)

In summarizing this section, it is vital to mention that at high scale energy, there is weak interaction (gluon self-interaction) resulting in asymptotic freedom.⁶ This phenomenon is what brings about gluon jet production. At low energy, mesons and baryons undergo confinement due to strong interactions.⁷

Gluon Jets in Proton-antiproton Collision

By restriction ourselves to the initial state heavy hadronic collisions, the factorization theorem [8] gives us

$\frac{d σ}{d x} = \sum_{j i} f_{j} (x_{1}, Q_{i}) f_{k} (x_{2}, Q_{i}) \frac{d σ_{j k} (Q_{i}, Q_{f})}{d \dot{x}} F (\dot{x} \to x, Q_{i}, Q_{f})$ (9)

In order for the structure to be maintained by the proton via gluon jet discharge, two gluon exchange is a requirement. In this process, loop integral computation over large momenta can be used to find the contribution of the hard gluons. We can express this contribution in a mathematically form as

$\int_{Q} \frac{d^{4} q}{q^{6}} \sim \frac{1}{Q^{2}}$ (10)

In addition, in proton-proton (pp) collisions, gluon jet emission depends on the scale and can be illustrated as in Figure 1.

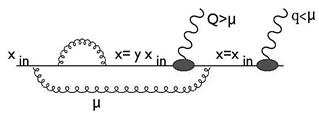
Figure 1 Gluon jet emission.

From Figure 1, the variation in the gluon jet emissions follows that

$f (x, Q) = f (x, μ) + \int_{x}^{1} d x_{i n} f (x_{i n}, μ) \int_{μ}^{Q} d Q^{2} \int_{0}^{1} d y P (y, Q^{2}) δ (x - y x_{i n})$ (11)

where P(y,Q²) is the probability of a quark emitting a gluon. The total derivative of Equation 11 then becomes

$\frac{d f (x, Q)}{d μ^{2}} = 0$ (12)

which implies that

$\frac{d f (x, μ)}{d μ^{2}} = \int_{x}^{1} \frac{d y}{y} f (y, μ) P (\frac{x}{y}, μ^{2})$ (13)

Thus, further computation proves that

$P (x, Q^{2}) = \frac{α_{s}}{2 π} \frac{1}{Q^{2}} P (x)$ (14)

Equation 14 brings us to the so called Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) equation described by

$\frac{d f (x, μ)}{d \log μ^{2}} = \frac{α_{s}}{2 π} \int_{x}^{1} \frac{d y}{y} f (y, μ) P_{q q} (\frac{x}{y})$ (15)

Thus the final evolution equation takes the form

$\frac{d f (x, Q)}{d t} = \frac{α_{s}}{2 π} \int_{x}^{1} \frac{d y}{y} [q (y, Q) P_{q q} (\frac{x}{y}) + g (y, Q) P_{q g} (\frac{x}{y})]$ (16)

while the gluon density one finally becomes

$\frac{d g (x, Q)}{d t} = \frac{α_{s}}{2 π} \int_{x}^{1} \frac{d y}{y} [g (y, Q) P_{g g} (\frac{x}{y}) + \sum_{q q \to q (y, Q)} P_{g q} (\frac{x}{y})]$ (17)

Gluon Jets in Electron-positron Collision

Let us consider a scenario as shown in Figure 2.

Figure 2 e+e-→Z.

This process results in the emission of a gluon as shown in Figure 3.

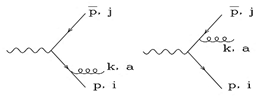
Figure 3 Emission of a gluon.

Thus, from Figure 3, the final amplitude for a soft gluon becomes

$A_{s o f t} =_{} \bar{v} (p) \in (k) (i g) \frac{- i}{p + k} Γ_{v}^{U} (p) λ_{i j}^{a} + \bar{v} (p) Γ^{U} \frac{i}{p + k} (i g) \in (k) v (p) λ_{i j}^{a}$
$= [\frac{g}{2 p . k} \bar{v} (p) \in (k) (p + k) Γ_{v}^{U} (p^{-}) - \frac{g}{(2 p^{-}) . k} \bar{v} (p) Γ^{U} (p + k) \in (p^{-})] λ_{i j}^{a}$ (18)

and by utilizing the Dirac Equation we obtain

$A_{s o f t} = g λ_{i j}^{a} (\frac{p . \in}{p . k} - \frac{p^{-} . \in}{p^{-} . k}) A_{B o r n}$ (19)

This shows that indeed positron-electron annihilations brings about gluon emissions resulting in the generation of gluon jets.

New physics

Today, Gluon jets evolution has given rise to more questions than answers in nuclear and particle physics. The quest to discover the fundamental particles under experiments has led to so many debates of whether the results are still under the confinements of the SM. This has led to physics beyond the SM which today is referred to NP. The main objective of theory and experiments is to search for phenomenology beyond the SM. The phenomena discussed in this paper of properties of heavy ion collisions provide us with a great opportunity to study hot and dense medium in our quest for NP. This is because in order to enter the QGP phase, we require matter that is interacting very strongly.

Conclusion

In conclusion, we wish to stress that in order for one to confront the infrared divergence in this computation and better understand such an expression, one must do some work in order to simplify it. This, as seen from above, is achieved by extracting such an expression and evaluating the divergent part of the integral. Thereafter a compulsory result can be arrived at. In addition, collisions are a very important component in the discovery of both new particles and their structures. Such collisions have given birth to the discovery of gluons as well as gluon jets. At the moment, it is not yet very clear how much energy is carried by gluon jets in view of each gluon involved. With this quest for NP, we hope this will soon be achieved.

Acknowledgments

I humbly forward my heartfelt diverse gratitude and appreciation to my supervisor, Dr. Davy Kabuswa Manyika, for his best mentorship. I would also like to thank my family members who supported me both directly and indirectly from the inception of the research work.