In this manuscript, we have performed an applied geomagnetic inversion study in the Chenar ferrous mine near Asadabad-Hamedan of Iran. The principal purpose of this study was to depict and visualize the ore massif of the Chenar ferrous mine in details and to find the suitable locations for geological drilling cores. In this study, 4300 Geomagnetic readings were acquired over a ten-day data acquisition period with a Canadian-built 2019 GEM-GSM19T magnetometer. The analyzes of the geomagnetic data in the Chenar ferrous mine successfully identified the susceptible zones in the area of study, and we have suggested the location of six drilling points in the mining area for further investigation and verifying of geophysical data. Our results depict four massifs which are extended as veins. According to the dimensions of the magnetic halos, our geophysical result estimates the ore deposit to be about two and a half million tons for three of the massifs in the Eastern part and 250 thousand tons for the fourth massif in the Western part of the study region.

Keywords: geomagnetic, geophysics, ferrous mines, exploration

Geomagnetic surveying is usually done nowadays to map a geological feature mainly at exploration stages detections of mines. The problem facing requires an inverse solution. The Gauss’ theorem¹ implies that if one knows the field distribution on a bounding surface, infinitely many equivalent sources distributions inside the boundary can produce the known field. Thus, any geomagnetic field measurement performed on the surface of the Earth can be reproduced by an infinitesimally thin zone of magnetic dipoles beneath the surface. From a mathematical perspective, this means there is no depth resolution inherent in magnetic field data. An approach for inverting geomagnetic data is to divide the Earth into a large number of cells of fixed size but of unknown susceptibility. Although the problem is not unique, if we choose an objective function for the model to fit the data using a global minimization technique such as,² minimization of a weighted model norm for a reference model is considered. This method allows the interpreter to guide the inversion by varying the weighting according to the available information³ choose to minimize the total volume of the causative body so that the final model is compact and structurally simple⁴ minimized the moment of inertia of the causative body for the centere of gravity or an axis passing through it. Their inversion result is guided by the estimate of the central depth and dip of the causative body. These approaches have merit, but they are not flexible enough to handle problems we are concerning. The⁵ presented an inverting method for magnetic data to recover 3-D susceptibility models. To allow the maximum flexibility for the model to represent geologically realistic structures, they discretized the 3-D model region into a set of rectangular cells, each having a constant susceptibility. The number of cells is generally far greater than the number of the data available, and thus they solved an underdetermined problem. Solutions are obtained by minimizing a global objective function composed of the model objective function and data misfit. The algorithm can incorporate a priori information into the model objective function by using one or more appropriate weighting functions. The inversion model can be either susceptibility of its logarithm. If susceptibility is chosen, a positivity constraint is imposed to reduce the nonuniqueness and to maintain physical realizability. In this study, we use the⁵ method to delineate the magnetic ores in the study area. The study presented here is typical and similar studies can be done to detect various ferrous mines.

The Chenar ferrous mine is located within the 5 km vicinity of Chenar village placed in 16 km north of Asadabad city of Hamadan Province of Iran. The access road to the mine is the road which connects the Chenar village to Asadabad city. The geographical location and the access road to Chenar ferrous mine are shown with green colour in Figure 1 (A). The area of interest is shown in red colour. A selected portion of Figure 1 (A) is shown in Figure 1 (B). The black box indicated in Figure 1 (B) is the top view projection of an imaginary box used to illustrate our analysis. The data was acquired in 4300 pre-planned location using a Canadian GEM-GSM 19 T series magnetometer in 10 days. The spatial resolution of the data in each line was 20 meters Figure 1 (C).

Figure 1 (A) Location of the study mine in the satellite image and the way of green access to the mine. (B) The black box shows the top view of the analysis cubes in the study area. (C) The data acquisition points where the magnetometer was placed and recorded the magnetic value of the Earth.

Variogram and magnetic intensity

The background Gamma intensity in the study area is 47847 gammas. The lowest and the highest recorded values are 39319 and 54650 gammas, respectively. Therefore, a positive range of 8528 and a negative range of 6803 gammas can be considered to illustrate the residuals from background gamma intensity.The data was transferred to the processing Computer; and various corrections were done, including outlier data reduction to reach a modified data. Figure 2 (A) shows the variogram of the magnetic data and Figure 2 (B) shows the total geomagnetic intensity map in the study area.

Figure 2 (A) Variogram of magnetic data of Chenar ferrous mine. (B) Total Geomagnetic Intensity map of the Chenar ferrous mine.

Although Figure 2 (B) provides the visual information, it is better to use the local anomaly map by applying the residual filters which are the difference between the total geomagnetic intensity with the local geomagnetic intensity to map the anomalies Figure 3 (A). In geomagnetic explorations, regional anomalies are usually removed in order to better show the remaining anomalies from the observed anomalies. In anomaly maps showing the potential field, the effects of deep masses have a large contribution, and conversely, the surface effects would include only on small areas. Therefore, the residual anomaly values will be expressed according to Eq.1:

$A_{residual}=A_p–A_{regional}$ (1)

Where A_residual is the residual anomaly, A_p is the potential field anomaly, and A_regional is the regional anomaly. The local anomaly map is a basic map for all further calculations, modelling and generating of other geomagnetic maps and sections of the mine. The transfer to pole method is used to analyze geomagnetic data Figure 3 (B). The shape of a magnetic anomaly depends on the physical dimensions, magnetic susceptibility, polarization of the mass, and the direction of the regional field. For symmetric masses in the magnetic poles, where the directional field and polarization direction are perpendicular to each other, produces a symmetric anomaly. In reality, the geomagnetic anomalies are not symmetrical, and the directional field and polarization direction are not perpendicular in the location of data acquisition. Therefore, the transfer to pole method is used for removing asymmetries created by regional fields and non-vertical polarization. In other words, the transfer to pole method is used to eliminate the effects of deformation due to changes in inclination angles and deviation of magnetic polarization, assuming that the polarization is only due to the geomagnetism of the earth. If we remove the geomagnetic effect of the deep anomalies, we can detect the shallow anomalies. Derivative method is a powerful tool for detecting components with longer wavelengths in an anomalous field. In derivational maps, because of the linear properties of in-depth anomalies, the effect of regional and deep anomalies would fade away and become very weak, and the surface anomalies can be more clearly visible. The derivative method depicts the approximate form of the anomaly but disperses the amplitude of the anomaly. This method increases the noise and may show false anomalies which are unrelated to geology and also causes an increment in the gradients along the edges of shallow magnetic sources. Therefore, this method is often used to locate the edges of magnetic deposits and detect shallow sources Figure 3 (C). In order to depict the limits of the anomaly, we use the analytical signal method. The value of the analytical signal function is calculated at all grid points of the network, and its maximum value represents the corners of the subsurface anomaly Figure 3 (D).

Figure 3 (A) Map of local anomalies. (B) Map of Transfer to pole. (C) Map of the vertical derivatives. (d) Analytical signal map.

By the aid of downward extension method, the potential field data are mathematically projected from a primary base surface to another surface below the primary base surface. This method increases the effect of high wavenumber components and sources of surface anomalies. This method is a powerful tool for studying near-surface sources; its usefulness depends on how to eliminate the noise that can cause instability of the answers. The results of the downward expansion method will be highly questionable when there is inherent uncertainty in the position and size of the geological structures represented by the magnetic intensity data Figure 4 (A). The upward extension method in magnetic field data is widely used in geophysics to augment and detect more in-depth source responses where shallower sources are also available. In this method, potential field data are mathematically projected from a base surface to level surfaces above the primary base surface. Thus the surface effects are eliminated, and the depth effects are defined more clearly (precisely opposite of the downward extension). This method eliminates anomalies with shorter wavelengths and reduces the amplitude of the anomalies and reduces noise. Therefore, this method works as a low-pass filter. The upward extension method seems noiseless comparing to the downward extension method Figure 4 (B–D).

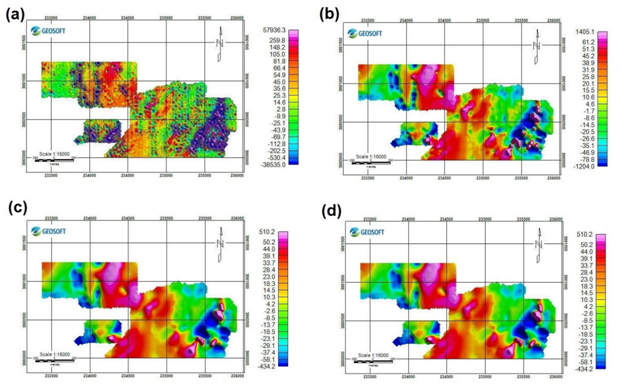
Figure 4 (A) Downward continuation map to 8 m. (B) Upward continuation map to 20 m. (C) Upward continuation to 40 m. (D) Upward continuation to 80 m.

Geomagnetic inversion modeling

We use the⁵ algorithm for 3D inversion of the magnetic anomalies. In this inversion approach, an initial value is considered for the searching variable, which is itself a function of self-sufficiency of the searching magnetic anomaly. Next, a multi-component objective function is constructed that has sufficient flexibility to produce a variety of models. This objective function deals to minimize the roughness in three spatial directions and has a three-dimensional weight based on the distribution of magnetic susceptibility with depth. Auxiliary functions for 3D weighting in the objective function can be used to combine more information about the model. Such information may be obtained from other geophysical data, geological data, or the interpreter's quantitative and qualitative understanding of the geological structure and its relationship to the magnetic susceptibility of rocks. The numerical solution for this inverse problem is achieved by dividing the earth into a large number of cells. The final solution would provide a vision of the complex geological objects beneath the ground. Choosing proper initial guesses as the start of the inversion, including magnetic susceptibility, position, and shape of the searching object can lead us to a more realistic model.

The⁵ starts from Eq. (2):

$d=Gk$ (2)

Where d is the actual data, G is the sensitivity matrix, and k is the magnetic self-susceptibility of the rocks in an orthogonal, meshed block intended for inversion. The inverse problem is formulated as an optimization problem to reproduce an objective function of the model, given the limitations of the minimized equation and the data, with an acceptable error. Details and descriptions can be found in⁵ As it can be seen in the three-dimensional Figure 5(A) and two-dimensional shapes Figure 5(b,c), the final model is similar to this shape which has been obtained using 20-meter mesh blocks. Note that this model is definitely not entirely in line with the reality of the Earth, but it is the best model that has been obtained by the inversion method, which aids us about the formation and expansion of the ore deposits. The magnetic anomalies are shown in Figure 5(D,E). While Figure 5(E) remaps the area of interest with the black box, the detected ore deposits are shown in the Figure 5(G) by red colour.

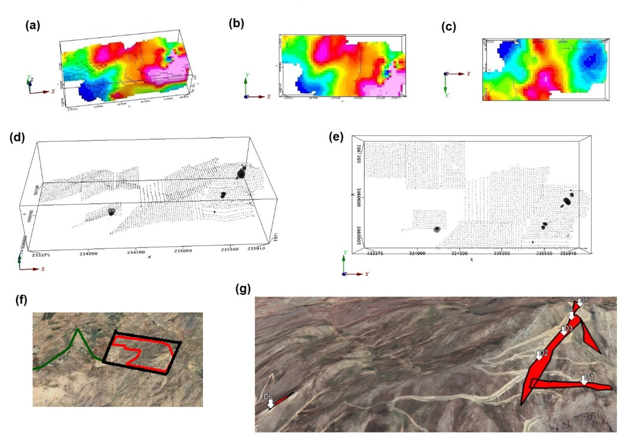
Figure 5 (A) A 3D numerical modelling of the magnetic data. (B) Plan view of (A). (C) Bottom view of (A). (D-E) 3D and plan view of detected Magnetite anomalies. (F) The black box shows the area considered in plots (A-E). (G) The final location of the four detected ore veins and the points proposed for drilling shown on the Google Earth map.

According to the data, maps and inverse modelling, the eastern part of the Chenar ferrous mine, three veins of magnetite (according to the figures of the magnetic field) with excellent quality and quantity have been identified. These three veins intersect at an angle with each other forming a 3D orthogonal structure, in other words, a massive ore has spread in three directions and is injected into its host rock Figure 5 (G). The centere of the largest vein (vein #1) including proposed drilling points D2-D5, which extends to the southwest, has a UTM coordinate of (235460,3860310). The length of this anomaly in the Northeast direction is 700 m, and its width in the east direction is about 30 m. The vein which has an extension to the west side including D1 (vein #2), has a length of 300 meters and a variable width of 30 meters. The centere UTM Coordinates of this vein is (235398,3860211), and this vein intersects vein #1. The last vein in the eastern part (vein #3) has a north-south direction, and its origin intersects with vein #1, the length of this vein is 200 meters in the north direction, and its width varies from 10 to 50 meters.

The total area of ​​these three anomalies is about 40,000 square meters. After the detection of these anomalies with geophysical inversion, a detailed search was conducted in the area with a high amount of magnetic susceptibility and the outcrops were identified. The thickness of the deposit match with the modelling and field observations and is about 15 meters. The geophysical estimated reserve deposit for these three veins can is estimated about two and a half million tons. The proposed drilling points to estimate the exact reservoir in the eastern part are shown in lines 1-5 of Table 1. Apart from the large anomaly mentioned in the western part of the mine, a small vein of magnetite was detected in the study region. The centre coordinates of this vein are (234270,3860308) with a length of 150 meters and a width of 5 to 10 meters. The Western vein is accessible from the ground and the thickness of the deposit according to the modelled dimensions, is about 6 meters. The geophysical estimation for this reservoir is about 25,000 tons and can be considered for this section, borehole D6 is intended for drilling in this section.

The data was acquired by the GeoMine company of Iran for Hamid Reza and Atisa Salahchin. The geomagnetic inversion analysis was done using GeoSoft® software. We would like to thank our colleagues in the GeoMine Company of Iran, North Drilling company of Iran, and International Institute of Earthquake Engineering and Seismology for their useful help in this manuscript.

The author declares there is no conflict of interest.

1. Gauss CF. Theoria Attractionis Corporum Sphaeroidicorum Ellipticorum Homogeneorum Werke. Springer. 1877. p. 3–22.
2. Green WR. Inversion of gravity profiles by use of a Backus-Gilbert approach. Geophysics. 1975;40(5):763–772.
3. Last B, Kubik K. Compact gravity inversion. Geophysics. 1983;48(6):713–721.
4. Guillen A, Menichetti V. Gravity and magnetic inversion with minimization of a specific functional. Geophysics. 1984;49(8):1354–1360.
5. Li Y, Oldenburg DW. 3-D inversion of magnetic data. Geophysics. 1986;61(2):394–408.