In this paper the formation and characterization of non uniform single side loaded and double side loaded optical gratings is done. The non uniform long period reversible optical grating is practically induced in communication grade single mode fiber. In reversible optical fiber gratings the fiber is subject to periodical stress, which results in alternated regions under compression and stretching that modulate the refractive index via the photo elastic effect. The spectral responses of single side loaded optical grating is then compared with double side loaded optical grating.

Keywords: reversible gratings, non uniform grating, single sided loading, double sided loading

Long period fiber grating (LPFG) can be realized with permanent modification of fiber such as UV induced refractive index changes and etching or temporary alternation of fiber propagation characteristics. LPFG by UV light exposure with amplitude phase mask are popular, but their spectra can hardly be tuned once they have been fabricated, which may limit applications of LPFG. The temporary or reversible grating can be implemented through the application of acoustic wave to the fiber^1,2 or periodical loading onto the fiber.³ Reversible optical fiber gratings need neither a special fiber nor an expensive writing device for fabrication. These gratings also offer advantages of being simple, inexpensive, erasable, reconfigurable, and also give flexible control of transmission spectrum. Depending upon refractive index profile and grating period variation, gratings are of different types. The grating period can be uniform or graded, and either localized or distributed in structure. Uniform optical fiber grating yields highly undesirable side-lobes due to the sharp boundaries of the grating.⁴ A well-discussed method to reduce these side lobes is to apodize the grating coupling strength along the grating by gradually tapering the refractive index modulation amplitude to zero at both end of the grating. Periodic refractive index perturbations in an optical grating with single sided loading could be primarily stress induced, since the points of stress would be those where the plate presses the fiber against the grooved plate. While in an optical grating with double sided loading refractive index perturbation is due to the periodic microbend.

Non uniform (apodized and chirped) gratings are modeled mathematically in the following section.⁴ Consider a bare three-layer step-index fiber that has a core with an index of 1.45 and a radius of 4.15μm, a cladding with an index of 1.444 and a radius of 62.5μm. The surrounding medium is air. A non uniform grating in this fiber is divided into a number of concatenated uniform grating sections, and the coupling strength, period and the resonance wavelength are allowed to vary from section to section. It has following effective index variation along the core of a fiber as shown in Figure 1.

Figure 1 Multisection Apodized LPFG with (a) varying average index along the length of grating    (b) varying period along the length of grating.⁴

$\Delta n(z)=\Delta n_{dc}(z)+\Delta n_{ac}(z)\sin \left(\frac{2\pi z}{\Lambda }+\phi \right)$ (1)

Where z is distance along fiber $\left(0\le z\le L\right)$ , L is grating period, L is grating length, $\Delta n_{dc}\left(z\right)$ is background index variation, $\Delta n_{ac}\left(z\right)$ is grating amplitude variation, $\phi$ is a constant phase. The dc component $\Delta n_{dc}\left(z\right)$ can be positive or negative, while the ac amplitude $\Delta n_{ac}\left(z\right)$ is taken to be positive. $\Delta n_{dc}\left(z\right)$ and $\Delta n_{ac}\left(z\right)$ are slowly varying functions of z. The grating has 8 sections with lengths $z1,z2,z3,z4andz4,z3,z2,z1$ with different periods. Over the spectral range of interest, LP01 core mode couples to 2, LP0m (m>1) cladding modes. A nominal resonance wavelength of ideal apodized LPFG that has $\Delta n_{dc}\left(z\right)=0$ is given by following equation,

${\lambda }_0=\left[N_{01}({\lambda }_0)-N_{0m}({\lambda }_0)\right]\Lambda$ (2)

Where N01 and N0m are the effective indices of LP01 and LP0m modes of fiber in absence of grating. In presence of average index variation effective indices and grating periods in different sections are in general different, which results in different resonance wavelengths. The resonance wavelength in i^th section is

${\lambda }_{0i}=\left[N_{01}({\lambda }_{0i})-N_{0mi}({\lambda }_{0i})\right]\Lambda$           (3)

${\lambda }_{0i}$  is larger or smaller than λ0 depends on sign of dc index change and sign of modal dispersion factor γ.

${\lambda }_{0i}={\lambda }_0+\gamma \Delta n_{dci}({\eta }_{01}-{\eta }_{0m})\Lambda$ (4)

$\gamma =\left[1-\Lambda (\frac{d{N}_{01}}{d\lambda }-\frac{d{N}_{0m}}{d\lambda })\right]$   (5)

Where

${\eta }_{01}\&{\eta }_{0m}$  are confinement factor of LP01 and LP0m mode in core area.

$\begin{array}{l}\Delta n_{dc}(z)=a_{0}A(z)\\ \Delta n_{ac}(z)=a_{1}A(z)\end{array}$         (6)

Where A (z) is normalized apodization profile function, a0 & a1 are amplitudes of corresponding index changes. In an apodized LPFG having dc index variation, the spread of the resonance wavelength depends on value of modal dispersion factor γ. For a typical fiber, γ is positive for low-order cladding modes and negative for high-order cladding modes [5]. For a positive dc index change, a positive γ gives red shift in resonance wavelength i. e. a red shift is observed for low order cladding modes. While for a negative dc index change, a negative γ gives blue shift in resonance wavelength i. e. a blue shift is observed for high order cladding modes.⁶

Characterization of non uniform gratings

Hardened steel block of 7x2x1cm (L x W x T) with periodical corrugations on L x W plane were prepared. Circular grooves of 50% duty cycle, 800μm in depth and varying period (600-2400μm) were fabricated with mechanical processes. A commonly used communication fiber (corning SMF-28) is used in experimentation. The experimental set up is as shown in Figure 2. Single sided loading is done; the bottom plate is plain, while the upper plate is specially designed corrugated plate. For characterization the light from broadband superluminacent LED with output power of -8dBm, center wavelength 1530nm and bandwidth of 69nm was passed through the grating under test and the transmitted signal was analyzed with the help of optical spectrum analyzer covering the wavelength range from 1250nm to 1650nm. Coupling coefficient can be adjusted through changing the pressure applied on the fiber. Because of photo-elastic effect and microbend effect, the pressure controls the refractive index modulation depth, and changes the coupling state between the core and the cladding modes.^3–7 Another way to obtain apodization is by changing the pressure distribution along the grating length.8 Respective changes in ac and dc index are shown in Figure 1.

Figure 2 Experimental set up for characterization of single sided loading of fiber.

Double sided loading in reversible gratings

Fill In an optical grating with double sided loading refractive index perturbation is due to the periodic microbend as shown in Figure 3. The experimental set up is as shown in Figure 4. The bottoms as well as the upper plate are identical corrugated plates with 1200µm plain corrugations. For characterization the light from broadband superluminacent LED was passed through the grating under test and the transmitted signal was analyzed with the help of optical spectrum analyzer covering the wavelength range from 1250nm to 1650nm.The positions and depths of transmission spectral depressions varied with pressure applied on grating as shown in Figure 5 and Figure 6.

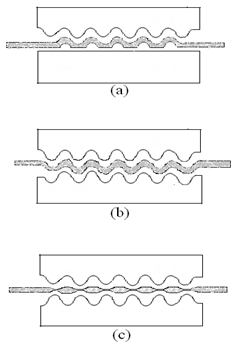
Figure 3 Fiber deformations in (a) single sided loading (b) double sided loading for π relative phase between two plates (c) double sided loading for 0 relative phase between two plates (crest to crest matching).

Figure 4 Fiber deformations in (a) single sided loading (b) double sided loading for π relative phase between two plates (c) double sided loading for 0 relative phase between two plates (crest to crest matching).

Figure 5 Transmission spectrum of reversible LPFG (L=1200μm) with π relative phase.

Figure 6 Transmission spectrum of reversible LPFG (L=1200μm) with 0 relative phase.

In double sided loading the positions and depths of transmission spectral depressions varied with pressure applied on grating. Another interesting observation in double sided grating is the appearance of new peaks. In this configuration, one clearly induces microbends in the fiber, which is different from the case where the fiber is pressed with a flat surface on one side. When the two periodical structures are exactly in phase i. e. crests are exactly matched, all spectral depressions start gradually disappearing (broadened and reduced amplitude) with increase in load.

This work is partially supported by the Department of Science and Technology of India.

1. R Faced, C Alegria, MN Zervas. Acoustooptic attenuation filters based on tapered optical fibers. IEEE J Sel Top Quantum Electron. 1999;5(5):1278–1288.
2. WF Liu, IM Liu, LW Chung, et al. Acoustics induced reflection wavelength switching in a fiber Bragg grating. Opt Lett. 2000;25(18):1319–1321.
3. S Savin, MJF Digonnet, GS Kino, et al. Tunable mechanically induced long period fiber gratings. Opt Lett. 2000;25(10):710–712.
4. Sunita P Ugale, Vivekanand Mishra. Formation and characterization of non uniform long and ultralongperiod reversible optical fiber gratings. Optik. 2014;125:3822–3824.
5. X Shu L, Zhang, I Bennion. Sensitivity characteristics of long-period fiber gratings. Journal of Lightwave Technology. 2002;20(2):255–266.
6. Yanju GU and Kin Seng CHIANG. Effects of Average Index Variation in Apodized Long-Period Fiber Gratings. Photonic Sensors. 2013;3(2):102–111.
7. Cong Yin, Xiaojun Zhou, Zhiyao Zhang, et al. Second order optical differentiator based on a mechanically induced LPFG with a single π-shift. Frontiers of Optoelectronics. 2012;5(3):261–265.
8. Chen Kai, Sheng Qiu-Qin, Dong Xiao-Yi. A new method for Filter Design based on Long-Period Fiber Grating. Chin Phys Lett. 2004; 21(2):332.