Cluster size distribution to characterize the first–order phase transitions of equilibrium systems

doi:10.15406/paij.2018.02.00112

eISSN: 2576-4543

Physics & Astronomy International Journal

Research Article Volume 2 Issue 4

Cluster size distribution to characterize the first–order phase transitions of equilibrium systems

Lima FWS

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Department of Physics, Federal University of Piaui, Brazil

Correspondence: Francisco Welington De Sousa Lima, Department of Physics, Dietrich Stauffer Computational Physics Lab, Federal University of Piaui, 64049?550, Teresina?PI, Brazil, Tel 5586 3237 1424

Received: July 30, 2018 | Published: August 17, 2018

Citation: Lima FWS. Cluster size distribution to characterize the first–order phase transitions of equilibrium systems. Phys Astron Int J. 2018;2(4):375-376. DOI: 10.15406/paij.2018.02.00112

Download PDF

Abstract

Through Monte Carlo simulations we study cluster size distribution (CSD) of equilibrium systems. The system is simulated by applying the Wolff algorithm or single cluster Monte Carlo update algorithm. Our results show that CSD is a good tool in the identification of first–order transitions.

Keywords: phase transition, potts model, clusters, wolff

Introduction

Equilibrium systems such as the Potts model with q–states in two–dimension presents two types of phase transition. Continuous or second order and one explosive or first order.^1,2 To identify the type of phase transition we have some useful tools such as examining the minimum free energy^3,4 by considering the probability distribution of energy,⁵ the distribution function of the system order parameter PDF,^6,7 fourth–order Binder cumulant^8,9 and CSD.^10–12

In systems that exhibit first–order phase transition the most common feature is the coexistence of ordered and disordered states in the phase transition region. In the region of ordered phase the large clusters are dominant and in the disordered phase, small clusters are dominant. The existence of both small and large clusters in a first–order phase transition region gives rise to double–peak energy behavior and PDFs. Studying the Potts model in two dimensions Aydin et al.,¹⁰ and Gündüç et al.,¹¹ observed that global operators related to cluster size are more sensitive to structural changes in a phase transition than energy–related local operators and the order parameter of the system. Notably, the CSD may give a better indication of the order of phase transition for small networks than the distribution of energy.

In this work, we investigate the CSD to study the phase structure of the 8–state Potts model on Voronoi–Delaunay random lattices (VDRL)¹³ concerning quenched randomness on the links in a range of alpha values a= 0 to 0.5

Model and simulations

We consider the Potts model whit q=8 states on VDRL by a set of spin variables taking the values situated on every site i of a VDRL with N sites. In this random lattice, we start from a two–dimensional random lattice consisting of sites linked to their k (where 3<k<20) and different for each site of network nearest neighbors by both outgoing and incoming links.

The Hamiltonian of the Potts model whit q=8 states can be writen as

$- KH= \sum_{i,j} J_{ij} δ_{σ_{i} σ_{j}}$ (1)

where $K= 1 / k_{B} T$ , T is the temperature $δ_{σ_{i} {,σ}_{j}}$ ,is the delta of Kronecker $k_{B}$ ,is the Boltzmann constant, the sum goes over all nearest–neighbors pairs of sites. Here, we assumethat the coupling factor $J_{ij}$ depends on the relative distance $r_{ij}$ between sites i and j and is given by

$J_{ij} {=J}_{0} e^{- {ar}_{ij}},$ (2)

where $J_{0}$ is a constant and $a \geq o$ a model parameter. In the simulations, we apply the Wolff update algorithm^14–17 on differents VDRL to generate different sizes of the cluster and perform simulations comprising a number N= 4000 of sites of random lattices. For each system quenched averages over the connectivity disorder are approximated by averaging over R=100 independent realizations. For each simulation, we have started with a uniform configuration of spins. We ran 3x10⁵ Monte Carlo steps (MCS) per spin with 2X10⁵ configurations discarded to reach steady state.

Results and discussions

From CSD we calculate the average cluster size defined by

ACSD= \frac{1}{N_{C}} 〈 \sum_{i= 1}^{N_{C}} C_{i} 〉

(3) where

N_{C}

and

C_{i}

are the number and sizes of clusters generated by the Wolff algorithm, respectively. In the above equations

< ... >

stands for thermodynamic averages. In Figure 1 we show the histogram of the energy for the values

a = 0.1, 0.15, 0.29, 0.23, 0.25, 0.27, 0.50

and for

N = 4000

sites. From

a = 0.0

0.20

we have a double peak structure indicating that a first order phase transition to the Potts model

q = 8

with states, while for

a = 0.5

we have a single Gaussian peak structure that represents an indication for a second order phase transition. To further clarify this behavior we use the mean distribution of clusters as seen in Figure 2. As shown in Figure 2 the peaks in the region of small clusters indicate the presence of first–order transition.

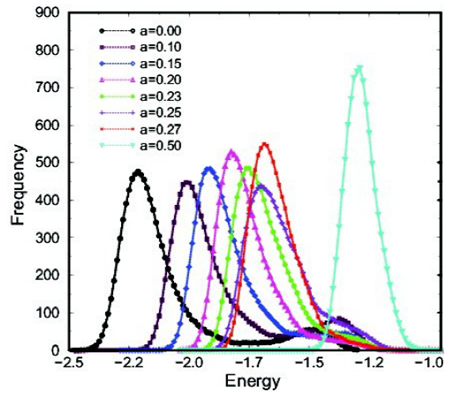
Figure 1 Histogram of the energy for some values of $a = 0.1, 0.15, 0.29, 0.23, 0.25, 0.27, 0.50$ and $N = 4000$ sites.

Figure 2 Distribution of the average sizes of clusters to several values of a on a VDRL of sites $N = 4000$ and with $q = 8$ .

Conclusion

In summary, the energy histogram is very useful in identifying a first–order phase transition as long as the systems structures are regular as the square lattice, triangular, and other two–dimensional archimedean lattices. In the case here, that is, on VDRL or others random lattices where the Wolff algorithm can be used we have seen that the ASCD is more appropriate for the identification of first–order phase transitions.