
Research Article Volume 2 Issue 1
Charged wormholes supported by 2-fluid immiscible matter particle
Islam S,1
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Shaikh A,1 Das TK,1 Rahaman F,2 Rahaman M2
1Faculty of Physics, Harish-Chandra Research Institute, India
2Department of Mathematics, Jadavpur University, India
Correspondence: Farook Rahaman, Department of Mathematics, Jadavpur University, Kolkata 700032, India, Tel 9831907279
Received: December 15, 2017 | Published: January 19, 2018
Citation: Islam S, Shaikh A, Das TK, et al. Charged wormholes supported by 2-fluid immiscible matter particle. Phys Astron Int J. 2019;2(1):39-46. DOI: 10.15406/paij.2018.02.00046
Download PDF
Abstract
We provide a 2-fluid immiscible matter source that supplies fuel to construct wormhole spacetime. The exact wormhole solutions are found in the model having, besides real matter or ordinary matter, some quintessence matter along with charge distribution. We intend to derive a general metric of a charged wormhole under some density profiles of galaxies that is also consistent with the observational profile of rotation curve of galaxies. We have shown that the effective mass remains positive as well as the wormhole physics violate the null energy conditions. Some physical features are briefly discussed.
Keywords: general relativity, electric field, wormholes, stability, rotational velocity, energy conditions
Introduction
The existence of Lorentzian wormholes has been a speculative issue though there are views that it can exist at the planck scale of 10-35 meters.1 Though wormholes are designated as tunnels connecting two distinct universes or regions of the same universe but their actual physical significance was first proposed by Morris & Thorne2 and their possible locations in the galactic halo and central regions of galaxies further studied by Rahaman F et al.3,4 Exact solutions of the wormhole with extra fields such as scalar field and static electric charge have been studied by Kim SW et al.,5 and derived self-consistent solutions. We are acquainted with the fact that wormhole spacetimes are predictions of the GTR and need to be supported by observations. The modified extended metric for the charged wormhole model of Kim and Lee has been developed by Kuhfittig PKF6 to represent a charged wormhole that is compatible with quantum field theory. The field equations without the charge Q have been studied by Buchdahl7 who found physically meaningful solutions.
Kuhfittig PKF et al.,8 studied the modified wormhole model in conjunction with a noncommutative-geometry background to overcome certain problems with traversability. Further in view of quantum field theory, the modified metric in6 is studied as a solution of the Einstein fields equations representing a charged wormhole. Stable phantom-energy wormholes admitting conformal motions is discusssed in.9 Here it is shown that the wormhole is stable to linearized radial perturbations whenever
. The author has also studied macroscopic traversable wormholes with zero tidal forces inspired by noncommutative geometry10 where it is shown that whenever the energy density describes a classical wormhole, the resulting solution is incompatible with quantum-field theory.
The Friedmann-Robertson-Walker model with a wormhole has been studied by Kim SW11 and found the total matter to be nonexotic, while it is exotic in the static wormhole or inflating wormhole models, considering the matter distribution of the wormhole shape function as divided into two parts. The flare-out condition for the wormhole with the Einstein equation and the finiteness of the pressure is discussed.12 The possibility that inflation might provide a natural mechanism for the enlargement of Lorentzian wormholes of the Morris-Thorne type to macroscopic laws size has been explored by Roman TA.13 An analytical electrically charged traversable wormhole solution for the Einstein Maxwell-anti-dilaton theory as well as the deflection angle of a light-ray passing close to this wormhole has been discussed by Goulart P.14
The traversability of asymptotically flat wormholes in Rastall gravity with phantom sources is studied in.15 It is also observed16 that cosmic acceleration with traversable wormhole is possible without exotic matter like dark and phantom energy unless the scale factor of the universe obeys a power law dominated by a negative fractional parameter. 7-dimensional universe and the existence of a static traversable wormhole solution in the form of the Lovelock gravity are studied by El-Nabulsi RA.17 The cosmological implications of a four-dimensional cosmology dominated by quintessence with a static traversable wormhole by means of an additional bimetric tensor in Einsteins field equations is discussed in.18 Extra-Dimensional cosmology with a traversable Wormhole has been studied in.19 The author discuss many features of a higher-dimensional cosmology with a static traversable wormhole dominated by a variable effective cosmological constant and depending on the scale factor
.
Hererra L20 has investigated the conditions under which general relativistic polytropes for anisotropic matter exhibit cracking and/or overturning. The dynamics of test particles in stable circular orbits around static and spherically symmetric wormholes in conformally symmetric spacetimes is discussed in.21 In this paper we thrive to derive a general metric of a charged wormhole under some density profiles of galaxies which should also be consistent with the observational profile of rotation curve of galaxies.
The stress in this paper is on the anisotropic matter distribution where we have considered a combined model of quintessence matter and ordinary matter along with charge distribution. A valid wormhole also exists under the isotropic condition where
. We iterate that such a combination could in fact support a wormhole in Einstein-Maxwell gravity. One could also like to invite the prospect of theoretical construction of such wormhole with the assumption of zero tidal forces.
The aim of our paper is envisaged as follows:
In section 2. We have solved the Einstein-Maxwell field equations pertaining to our proposed metric and deduce the wormhole solutions. Section 3. Deals with the profile curve and the embedding diagram. The geodesics study in section 4. Reveal the observational phenomena pertaining to gravity on the galactic scale which is attractive. In section 5 & 6. We study the equilibrium conditions and the effective gravitational mass. Energy conditions and tidal forces are discussed in sections 7. The validity of our metric is further confirmed in our study of wormhole in the Galactic Halo region in section 8. The study ends with a concluding remark.
A particular class of solutions
We propose a general wormhole spacetime metric with charge for circular stable geodesic motion in the equatorial plane to be represented by the line element
(1)
Here
and
are the effective redshift function and effective wormhole shape function having functional dependence on the radial coordinate r and
(2)
The effective redshift function and the effective wormhole shape shape function are chosen in such a way that it does not violate the wormhole flare-out conditions as defined below. Also the spacetime is asymptotically flat, i.e
as
. The presence of charge inflicts a minor change in the graph of
vs. r as against
vs. r, keeping in parity the desired wormhole flare-out conditions. We further show that for particular choice of the shape function and redshift function, the wormhole metric in the context does not violate the energy condition at or near the wormhole throat.
We consider the geometric units
, in the EM field equations and presumably set the wormhole spacetime with an effective and positive constant electric charge Q. Such a form of charge is valid in the wormhole metric as evident in.5 As the charge is static, there is no radiation by the fields. If
, the metric reduces to the form observed by Rahaman F et al.,3 and if also
along with
, it reduces to the more generalized form of Morris-Thorne wormhole.2 Further if
, it reduces to the RN black hole with a vanishing mass. Here
denote the characteristic scale radius and l is a constant defined by
, being the rotational velocity of a test particle in the same gravitational field in a stable circular orbit in the galactic halo region.3 The stability of such an orbit depends on the effective positive radial velocity and will be studied later.
The flare-out conditions need to be studied which prevent wormholes to be physical and making it open, thereby paving a way for traversibility. These are as: (1) There should be no event horizon, hence the redshift function,
should be finite. (2) The wormhole shape function should obey the conditions, (i)
for
being the throat radius (ii)
(iii)
(iv)
and (v) As
approaches 2M, the Schwarzschildt mass,1,22 which is the mass function of the wormhole. Hence
should be a positive function.
We propose that the matter sources consist of two non-interacting fluids, one being real matter in the form of perfect fluid and the second as anisotropic dark energy which is responsible for the acceleration of the universe.23
The following self consistent Einstein-Maxwell equations for a charged fluid distribution is proposed as,
(3)
Where
and
are the contributions to the effective energy-momentum tensor for matter fluid, exotic matter and charge respectively.
The most general energy-momentum tensor compatible with static spherical symmetry for anisotropic distribution of matter (the matter is exotic in nature and is a necessary ingredient for construction of wormhole, thereby violating the energy conditions) is,
(4)
Where
and
are respectively, effective matter-energy density, effective radial fluid pressure, effective transverse fluid pressure, four velocity, and radial four vector of the fluid element. The case
, corresponds to the isotropic fluid when the anisotropic force vanishes.
In our consideration, the four velocity and radial four vector satisfy,
.
From equations (3) and (4) we get the following set of equations,
(5)
(6)
(7)
Where
, and
are the contributions due to the presence of charge.
We consider that the dark energy radial pressure is proportional to the dark energy density24,25 as,
(8)
And the dark energy density is proportional to the mass density as,
(9)
As the universe expands at a fixed rate, the curvature of spacetime is constant. Hence the density of dark energy which is responsible for the expansion of the universe is also constant. Also from the first Friedmann equation, we find
, Here H is the Hubble parameter related with the expansion rate of the universe. This expansion rate is driven by mass density
.
We employ the following standard equation of state (EOS):
(10)
Where m is a parameter corresponding to normal matter.It needs to be verified if equation (1) satisfies the Einstein’s equation self-consistently or nor.
The Einstein-Maxwell field equations with matter distribution as equation (3), using equations (5)-(7), are analogous with the transformations,
(11)
(12)
(13)
Using equations (2), (8), (9) and (10), the above equations (11)-(13) reduce to,
(14)
(15)
And
(16)
The matter terms due to charge are given by,5
(17)
Hence from equations (14) and (15) we find,
(18)
Where p is a variable. The effective wormhole shape function is found as,
(19)
From eqns. (14) and (17) we get expression for the energy density function as,
(20)
The following relations are evident,
(21)
(22)
(23)
And a big expression for the dark energy tangential pressure as,
(24)
-
The wormhole shape function is plotted below [Assuming
].
It is evident from the Figure 1, that the throat occurs at
. The flare-out conditions,
and
is also satisfied. As the wormhole shape function
and the energy momentum tensor
self-consistently satisfy the E-M equations, hence the wormhole spacetime metric in equation (1) is valid (Figures 2–4).
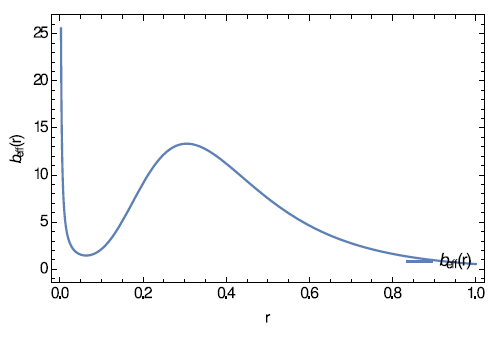
Figure 1 The shape function of the wormhole against
.
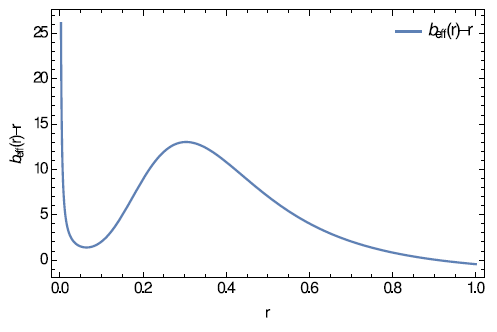
Figure 2 The throat occurs where
cuts the r-axis.
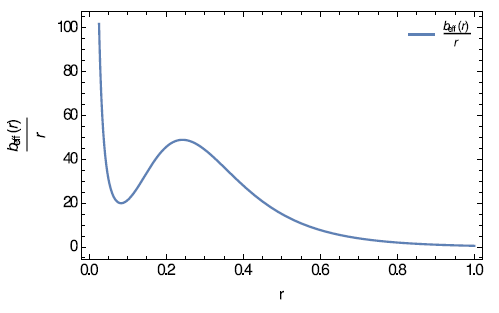
Figure 3
is plotted against
.
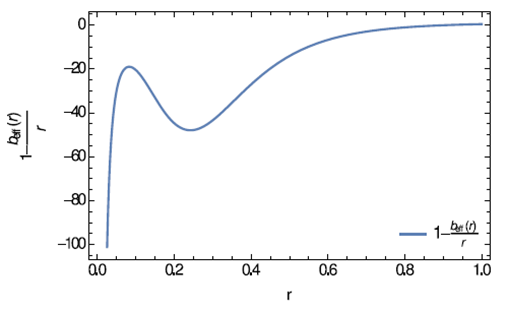
Figure 4
is plotted against
.
The electric field5 is given below and plotted graphically in Figure 5,
(25)
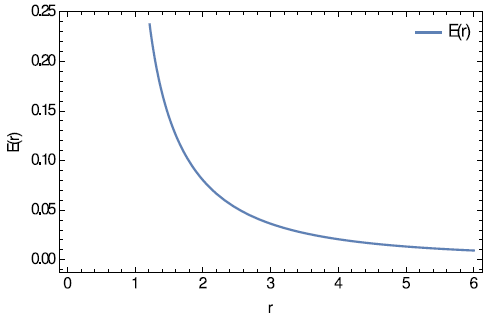
Figure 5 The elctric field is plotted against
.
The wormhole metric is valid throughout the galactic halo region. Also the test particle and the wormhole itself are in the same gravitational field of the galactic halo. Hence, the flat rotation curve for the circular stable geodesic motion of a test particle on the outer regions of the galactic halo and in the equatorial plane yields the tangential velocity26–28 as,
(26)
Using equation (2) we find,
(27)
The velocity profile is shown in Figure 6 which is also consistent as per observations,
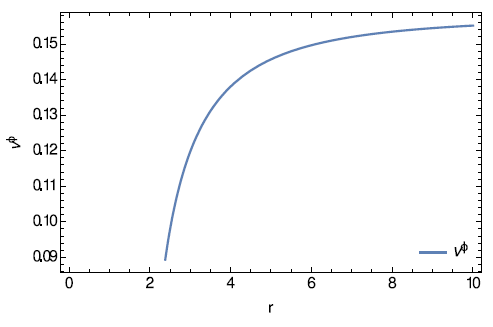
Figure 6 The velocity of galactic rotation curve is shown against
.
However, if
, then Q should also vanish simultaneously for a static and uncharged wormhole solution. For a positive circular rotational velocity, when i is considered as a parameter dependent on r we find,
(28)
Where the Lambert W-function also called omega function is the inverse function of
. For static and charged wormhole, l(r) decreases as r increases and is shown in Figure 7.
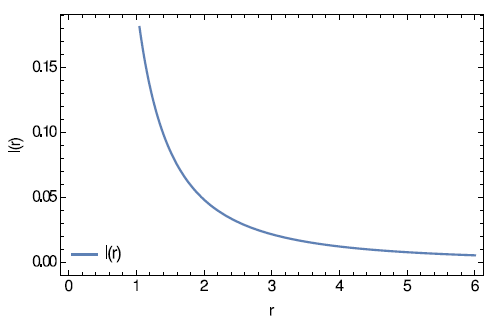
Figure 7 l(r) is shown against r.
Profile curve and embedding diagram of the wormhole
The profile curve is of the wormhole is defined by,2,29
(29)
The embedding diagram for a particular choice of parameters
, is obtained by rotating the profile curve about the z-axis as follows (Figure 8),
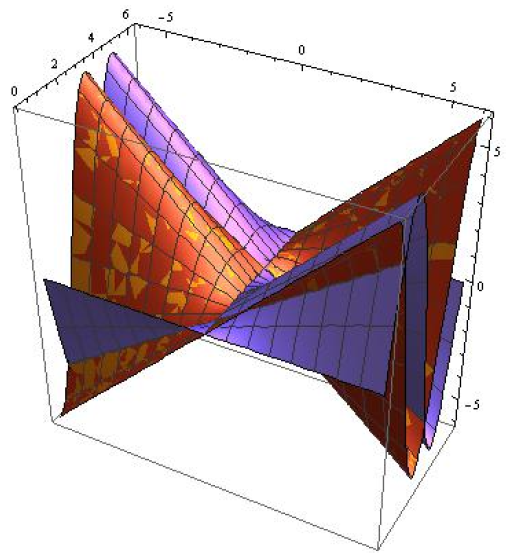
Figure 8 Embedding diagram of the wormhole.
We observe that the wormhole is valid in a particular region upto
, the throat occuring at
from its center.
According to Morris and Thorne,2 the r-coordinate is ill-behaved near the throat, but proper radial distance must be well behaved everywhere i.e. we must require that l(r) is finite throughout the spacetime. The proper radial distance L(r) from the throat to a point outside is
(30)
Which is always positive taking
.
Geodesic equations
We now study the geodesic equation for a test particle placed at some radius. The radial equation is found as,
(31)
Whereandare arbitrary constants. From the equations we find that
, is negative at
[considering
and
]. Also the quantity in the square bracket is positive. Hence the centrepetal force is directed towards the center of rotation indicating that the motion is stable. Thus particles are attracted towards the center. This result confirms with the observational phenomena pertaining to gravity on the galactic scale which is attractive (clustering, structure formation etc.).28
Equilibrium conditions
Following,30 we write the TOV Eq. for an anisotropic fluid distribution, in the following form
(32)
Where
the effective is gravitational mass within the radius and is given by
(33)
Which can easily be derived from the Tolman-Whittaker formula and the Einstein’s field equations. Obviously, the modified TOV equation (32) describes the equilibrium condition for the wormhole subject to gravitational (
) and hydrostatic (
) plus another force due to the anisotropic nature (
) of the matter comprising the wormhole. Therefore, for equilibrium the above Equation can be written as
(34)
Where,
(35)
(36)
(37)
(38)
Where the proper charge density
is given by,
(39)
The profiles of
and
for our chosen source are shown in Figure 9. The figure indicates that equilibrium stage can be achieved due to the combined effect of pressure anisotropic, electrical, gravitational and hydrostatic forces. It is to be distinctly noted that the anisotropic force is balanced by the combined effects of the forces electrical, gravitational and hydrostatic forces.
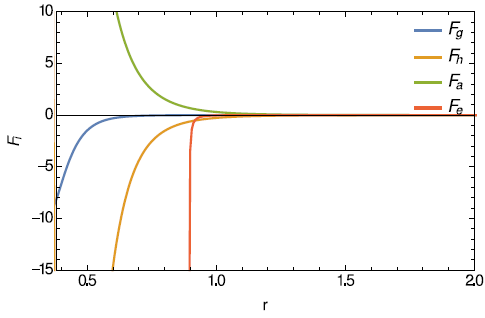
Figure 9 The various forces acting on the system in equilibrium are show against
.
Effective gravitational mass
In our model the effective gravitational mass, in terms of the effective energy density
, can be expressed as
(40)
The effective mass of the wormhole of throat radius, say,
upto
is obtained as
. One can observe that the active gravitational mass
of the wormhole is positive. This indicates that seen from the Earth, it is not possible to alienate the gravitational nature of a wormhole from that of a compact mass in the galaxy.
Energy conditions and tidal forces
We observe that
, which is in violation of the null energy condition to support wormholes. We observe that the wormhole has two distinct regions, in the region
, whereas in the region
as
(Figure 10).
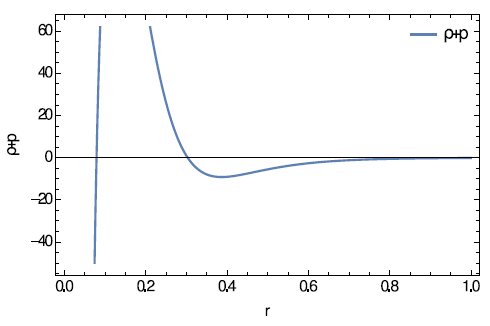
Figure 10 Null energy condition plotted against against r in k.p.c.
Density profile in the galactic halo region
We further consider the density profile of galaxies and their clusters in this region which takes the following form,31,32
(41)
Where
as defined earlier and
is the corresponding density, and search for further validity of our wormhole metric.
Hence the wormhole shape function is obtained from equation (14) as,
(42)
When,
(43)
We now consider the charge to be dependent on the wormhole shape function as,6
(44)
That is when,
(45)
Thus we get from equation (14),
(46)
Equation (17) and (46) implies,
(47)
And hence the wormhole charge within the throat radius is given by,
(48)
Which is constant for a suitable choice of positive parameter, n. The electric field is given by5
(49)
The wormhole shape function for suitable choice of parameters
and
is plotted below Figure 11,
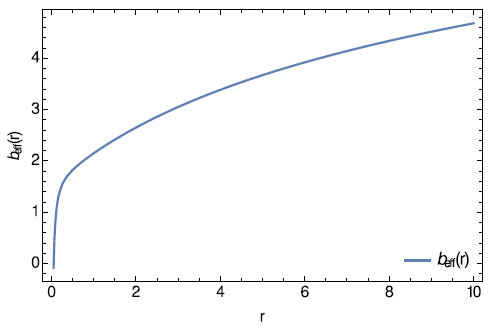
Figure 11 The shape function of the wormhole against r(
).
The other conditions are plotted in Figures 12 & 13, Figure 13 indicates that the throat of the wormhole occurs at
. Also as
, the conditions for a valid wormhole are satisfied.
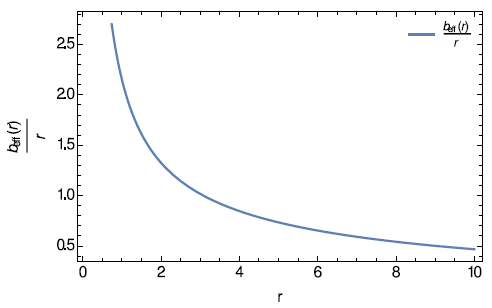
Figure 12 The asymptotic behaviour of shape function against
.
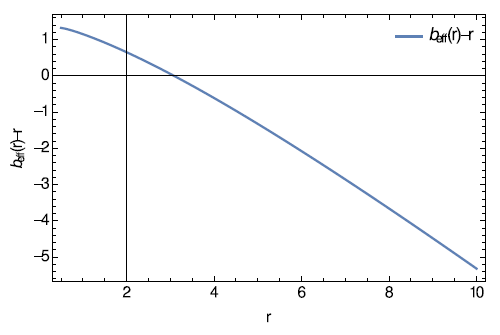
Figure 13 The throat occurs where
cuts the r-axis.
Final remarks
The possibility of generalizing the wormholes discussed here to wormholes with (slow) rotation has been discussed in.33 In the case of slow rotation a small nondiagonal polar-angle-time
component of metric is included. The
Einstein equation can be written using the tetrad components introduced with the basic 1-forms
26 and using
as,
(50)
Hence equation (1) is reduced to the self-sustained static wormhole metric,
(51)
Where
is the angular velocity of rotation. The static metric
is assumed to exist as a self-consistent solution of static semiclassical Einstein equations andis considered to be arbitrarily small.
We can also extend the original model of wormhole to a more generalized cosmological traversable wormholes by introducing the fifth coordinateas detailed in,34 such that
(52)
Thus using
equation (1) reduces to the 5-dimensional metric as,
(53)
It is known that the presence of a nonminimal interaction between dark matter and dark energy may lead to a violation of the null energy condition and to the formation of a configuration with nontrivial topology like a wormhole.35 Here the violation of N.E.C takes place only in the inner high-density regions of the configuration both between
and
.
The present observational data also suggest an exotic form of dark energy with equation of state
, violating the weak energy condition.36,37 This violation allows for exotic solutions of general relativity such as wormholes and warp drives and the possibility of time travel associated with them. Dark energy with
, is called super-quintessence or phantom energy.38
We observe via equation (1) that as the metric components are positive, the spacetime metric is devoid of any horizon resulting in a positive wormhole mass. Also the shape function is dependent on the charge Q, the characteristic scale length
, the corresponding density
and the positive constant n. Moreover for traversable wormhole the charge is considered sufficiently small yet positive for feasible geometric configuration. The validity of the metric is further confirmed by our extended study of wormholes in the galactic halo region. But whatever be the value of the charge the wormhole throat in our model occurs at a distance
from the center whereas in the Galactic Halo region the throat occurs at a distance
from the center for suitable choices of the above values. Hence we may conclude that any charge inside the wormhole is static in nature and could not affect any change in the wormhole configurations.
We iterate that such a metric is useful for wormhole study in other regions of the galaxy under different forms of gravity as well. Such study is in progress.
Acknowledgments
FR would like to thank the authorities of the Inter- University Centre for Astronomy and Astrophysics, Pune, India for providing the research facilities. FR and MR are also thankful to DST-SERB and UGC for financial support. We are grateful to the referee for his valuable comments.
Conflicts of interest
Authors declare there is no conflict of interest.
References
- Visser M. Lorentzian Wormholes. AIP Press, New York, USA. 1996.
- Morris MS, Thorne KS. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. American Journal of Physics. 1988;56(5):395–412.
- Rahaman F, Kuhfittig PKF, Ray S, et al. Possible existence of wormholes in the galactic halo region. The European Physical Journal C. 2014;74(2).
- Rahaman F, Salucci P, Kuhfittig PKF, et al. Possible existence of wormholes in the central regions of halos. Annals of Physics. 2014;350:561–567.
- Kim SW, Lee H. Exact solutions of a charged wormhole. Physical Review D. 2001;63(6).
- Kuhfittig PKF. On the feasibility of charged wormholes. Central European Journal of Physics. 2011;9(5):1144–1150.
- Buchdahl HA. General Relativistic Fluid Spheres. II. General Inequalities for Regular Spheres. Astrophysical Journal. 1996;160:1512.
- Kuhfittig PKF, Gladney VD. Noncommutative-Geometry Inspired Charged Wormholes with Low Tidal Forces. Journal of Applied Mathematics and Physics. 2017;5:574–581.
- Kuhfittig PKF. Stable phantom-energy wormholes admitting conformal motions. International Journal of Modern Physics D. 2017;26(3):1–8.
- Kuhfittig PKF. Macroscopic traversable wormholes with zero tidal forces inspired by noncommutative geometry. International Journal of Modern Physics D. 2015;24(3).
- Kim SW. Cosmological model with a traversable wormhole. Physical Review D. 1996;53(12):68890–6892.
- Kim SW. Flare-out condition of a Morris-Thorne wormhole and finiteness of pressure. Journal of the Korean Physical Society. 2013;63(10):1887–1891.
- Roman TA. Inflating Lorentzian wormholes. Physical Review D. 1993;47(4).
- Goulart P. Phantom wormholes in Einstein–Maxwell-dilaton theory. Classical and Quantum Gravity. 2017;35(2).
- Moradpour H, Sadeghnezhad N, Hendi SH. Traversable asymptotically flat wormholes in Rastall gravity. Canadian Journal of Physics. 2017;95(12):1257–1266.
- El-Nabulsi RA. Wormholes in fractional action cosmology. Canadian Journal of Physics. 2017;95(6):605–609.
- El-Nabulsi RA. Wormholes in Higher Dimensions with Non-Linear Curvature Terms from Quantum Gravity Corrections. Journal of the Korean Physical Society. 2011;59(5):2963–2970.
- El-Nabulsi RA. Quintessence cosmology with a traversable wormhole, massive decaying gravitons and with varying G and Lambda. Astrophysics and Space Science. 2010;325(2):277–281.
- El-Nabulsi RA. Extra-Dimensional Cosmology with a Traversable Wormhole. Chinese Physics Letters. 2009;26(9).
- Herrera L, Fuenmayor E, León P. Cracking of general relativistic anisotropic polytropes. Physical Review D. 2016;93(2).
- Böhmer CG, Harko T, Lobo FSN. Wormhole geometries with conformal motions. Classical and Quantum Gravity. 2008;25(7).
- Einstein A, Rosen N. The Particle Problem in the General Theory of Relativity. Physical Review journals Archive. 1935;48(1):1–5.
- Rahaman F, Maulick R, Yadav AK, et al. Singularity-free dark energy star. General Relativity and Gravitation. 2012;44(1):107–214.
- Kuhfittig PKF. Wormholes Supported by a Combination of Normal and Quintessential Matter in Einstein and Einstein-Maxwell Gravity. Journal of Modern Physics. 2013;4(1):30–34.
- Rahaman F, Saibal R, Islam S. Wormholes supported by two non-interacting fluids. Astrophysics and Space Science. 2013;346(1):245–252.
- Chandrasekhar S. Mathematical Theory of Black Holes, Oxford University Press, UK. 1983.
- Landau LD, Lifshitz EM. The Classical Theory of Fields. Pergamon Press, UK, 1975. p. 1–387.
- Rahaman F, Nandi KK, Bhadra A, et al. Perfect fluid dark matter. Physics Letters B. 2010;694(1):10–15.
- Morris MS, Thorne KS, Yurtsever U. Wormholes, Time Machines, and the Weak Energy Condition. Physical Review Letters. 1988;61(13).
- Ponce de León J. Limiting configurations allowed by the energy conditions. General Relativity and Gravitation. 1993;25(11):1123–1137.
- Novarro JF, Frenk CS, White SDM. The Structure of Cold Dark Matter Halos. Astrophysical Journal. 1996;462:563–575.
- Novarro JF, Frenk CS, White SDM. A Universal Density Profile from Hierarchical Clustering. The Astrophysical Journal. 1997;490(2):493–508.
- Khatsymovsky VM. Rotating vacuum wormhole. Physics Letters B. 1998;429(3–4):254–262.
- Kao WF, Soo C. A note on 4-dimensional traversable wormholes and energy conditions in higher dimensions. Cornell University Library, USA. 2003.
- Folomeev V, Dzhunushaliev V. Wormhole solutions supported by interacting dark matter and dark energy. Physical Review D. 2014;89(6).
- Faraoni V, Israel W. Dark energy, wormholes, and the big rip. Physical Review D. 2005;71(6).
- El-Nabulsi AR. Accelerated expansion of the Universe in the presence of a static traversable wormhole, extra-dimensions and variable modified Chaplygin gas. Astrophysics and Space Science. 2010;326(2):169–174.
- Pedro FGD, Prado MM. Wormholes in the accelerating universe. Cornell University Library, USA. 2007.

©2018 Islam, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


