For dealing with the MOLPRO, for example, the quality of results improves when one uses better basis-set, besides the use of the best available method. The best available basis-set is the aug-cc-pVnZ, where n denotes the number of zeta used. With the increase of the value of n, the requirement of memory-size and the computer-time becomes beyond the affordable limit. A possible solution for the requirement of memory-size and computer-time may be the extrapolation of basis-set, where two exponents α and β are used. These α and β are the indices for the power laws for reference energy (HF) and the energy of correlations (COR), respectively, are used. In the calculations, for a given system, the exponents are taken as constant. We find that the α and β are not constant, but vary from position to position in a system. Taking the case of calculation of potential energy surfaces, we have discussed the way for dealing with such situation. We have discussed the method for calculation of the values of α and β for various points in the system.

Keywords: ISM: molecules, potential energy surface, basis sets

For reliable results in the scattering phenomenon, accurate interaction potential is required.^1–7 The interaction potential may be calculated with the help of MOLPRO (Werner et al., 2012), for example, where one has to use the best available method and the best available basis-set. The best method available is the couple dcluster with Single and Double, and perturvative Triple excitations CCSD(T).⁸ The best basis-set available may be the aug-cc-pVnZ, where n denotes the number of zeta used and it stands for one of the D (Double-zeta), T (Triple-zeta), Q (Quadruple-zeta), 5 (Quintuple-zeta), etc. The prefix ’aug’ denotes the augmented version of the basis set. With the increase of n, the accuracy increases, and one would like to have n=∞. But, the requirement of memory size and computer-time increases extremely fast with the increase of n, which is not affordable, beyond n=6 (say). Truhlar⁹ proposed a nice concept for extrapolation of basis-set, where total energy is expressed as the sum of the reference energy (HF) and the energy of correlations.

$E^{tot}=E^{HF}+E^{cor}$ (1)

Each of the components of the energy is assumed to approach its basis-set limit according to the power laws:

${{\displaystyle E}}_n^{HF}={{\displaystyle E}}_{\infty }^{HF}+A^{HF}{n}^{-\alpha }$ (2)

And

${{\displaystyle E}}_n^{cor}={{\displaystyle E}}_{\infty }^{cor}+A^{cor}{n}^{-\beta }$ (3)

where the exponents α and β are the indices for the power law for HF and COR respectively and they are real and positive numbers. The energy with the suffix ∞ denotes the limiting value, corresponding to n=∞. The $A^{HF}$ and $A^{cor}$ are some parameters for the interacting system. The n has the values 2, 3 or 4 when the basis-set used are the aug-cc-pVDZ, aug-cc-pVTZ, aug-cc-pVQZ, respectively. Let use consider n=2 and n=3 and have

${{\displaystyle E}}_2^{HF}={{\displaystyle E}}_{\infty }^{HF}+A^{HF}{2}^{{}^{-\alpha }}$ (4)

And

${{\displaystyle E}}_3^{HF}={{\displaystyle E}}_{\infty }^{HF}+A^{HF}{3}^{{}^{-\alpha }}$ (5)

Equations (4) and (5) can be rearranged as (Truhlar, 1998) as

${{\displaystyle E}}_{\infty }^{HF}=\frac{3\alpha }{3\alpha -2^{\alpha }}{{\displaystyle E}}_3^{HF}-\frac{2\alpha }{3\alpha -2^{\alpha }}{{\displaystyle E}}_2^{HF}$ (6)

Similarly, for the energy of correlations, one can get (Truhlar, 1998)

${{\displaystyle E}}_{\infty }^{cor}=\frac{3\alpha }{3\alpha -2^{\alpha }}{{\displaystyle E}}_3^{cor}-\frac{2\alpha }{3\alpha -2^{\alpha }}{{\displaystyle E}}_2^{cor}$ (7)

Equations (6) and (7) show that by using the energies corresponding to n=2 and n=3, one can calculate the energies corresponding to n=∞, which one would like to have. This method of extrapolation is a nice idea and has been used for the calculation of potential energy surfaces (PES).¹⁰ In the calculations, the values of α and β are taken constant for all positions in the system.^9,10 In the present investigation, we find that the α and β are not constant, but they vary from position to position in the system. The effect of the variations of α and β is discussed. In section 2, we have presented the method for calculation of α and β. The effect of the variation of α and β is presented in section 3. Summary of the work is given in section 4.

Calculation of α and β

In order to calculate the values of α and β, we consider one more basis set corresponding to n = 4 in equations (2) and (3), to have

${{\displaystyle E}}_4^{HF}={{\displaystyle E}}_{\infty }^{HF}+A^{HF}{4}^{{}^{-\alpha }}$ (8)

And

${{\displaystyle E}}_4^{cor}={{\displaystyle E}}_{\infty }^{cor}+A^{cor}{4}^{{}^{-\beta }}$ (9)

That is, we have to perform calculations with one more basis-set, aug-cc-pVQZ. From equations (4), (5) and (8), we get

$\frac{{{\displaystyle E}}_4^{HF}-{{\displaystyle E}}_2^{HF}}{{{\displaystyle E}}_3^{HF}-{{\displaystyle E}}_2^{HF}}=F\left(\alpha \right)$ (10)

where

$F\left(\alpha \right)=\frac{4^{-\alpha }-2^{-\alpha }}{3^{-\alpha }-2^{-\alpha }}$ (11)

Similarly, for the energy of correlations, we get

$\frac{{{\displaystyle E}}_4^{cor}-{{\displaystyle E}}_2^{cor}}{{{\displaystyle E}}_3^{cor}-{{\displaystyle E}}_2^{cor}}=F\left(\beta \right)$ (12)

Where

$F\left(\beta \right)=\frac{4^{-\beta }-2^{-\beta }}{3^{-\beta }-2^{-\beta }}$ (13)

Equations (11) and (13) can be combined as

$F\left(\gamma \right)=\frac{4^{-\gamma }-2^{-\gamma }}{3^{-\gamma }-2^{-\gamma }}$ (14)

where $\gamma$  is either α or β, depending on the kind of energy. In Figure 1, we have plotted $F\left(\gamma \right)$ versus $\gamma$ . This is a smooth curve, and can be used for finding the value of $\gamma$ , corresponding to the known value of $F\left(\gamma \right)$ . For the known values of $E_2^{HF},E_3^{HF}$ and $E_4^{HF}$ we can calculate F(α) from equation (10), and corresponding to F(α), the value of α can be obtained from Figure 1. Similarly, for the known values of ${{\displaystyle E}}_2^{cor}$ , ${{\displaystyle E}}_3^{cor}$ and ${{\displaystyle E}}_4^{cor}$ , we can calculate $F\left(\beta \right)$  from equation (12), and corresponding to $F\left(\beta \right)$ , the value of β can be obtained from Figure 1. For better accuracy, this graphical method is replaced by the numerical interpolation.

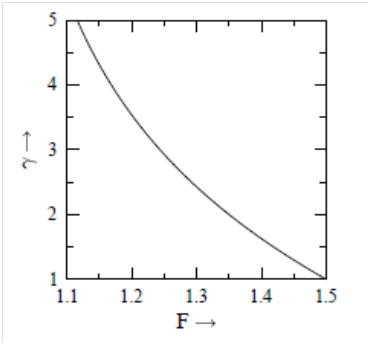
Figure 1 Variation of $F\left[=\left(4-\gamma -2-\gamma \right)/\left(3-\gamma -2-\gamma \right)\right]$ versus $\gamma$ . The F is plotted on the horizontal axis and $\gamma$ on the vertical axis.

We consider themolecule thioformaldehyde (H2CS), for example, whose identification¹¹ in some cosmic object was considered as an achievement, because earlier attempts made several times remained unsuccessful, though they were based on very accurate laboratory studies. For analyzing spectrum, one considers an appropriate number of energy levels. These levels are connected through radiative and collisional transitions between them. Calculation of collisional cross sections is the most difficult task in the investigation. But, the scientists are interested to have accurate cross sections for collisional transitions. The collisions are due to the most abundant molecule H₂. However, many scientists do not consider internal structure of H2, and therefore they replace H2 by the He atom,^2–7,12 as both of the H2 and He have two electrons and two protons, and the interaction potential depends on the charges of the interacting particles.^13–15 For the calculation of collisional cross sections, the interaction potential between the H2CS and He is required, for which the scientists are putting their best efforts. We have calculated interaction potential between the H2CS and He with the help of MOLPRO by using the best method CCSD (T) and three basis-sets, -cc-pVDZ, aug-cc-pVTZ and aug-cc-pVQZ, separately. The position of He atom relative to the center-of-mass of H2CS is expressed in terms of the spherical polar coordinates (r, θ, φ). The interaction potential between the H2CS¹⁶ and He is calculated for various positions (r, θ, φ). We have considered^17,18 532 positions specified by (r, θ, φ), with r=2 (0.25) 6.5 Å, θ=0◦ (30◦) 180◦, φ=0◦ (30◦) 90◦. The obtained values of α and β, are plotted in Figure 2 and Figure 3, respectively, as a function of position. Figure 2 and Figure 3 show that neither α nor β is constant. Both of them vary from position to position in the system.

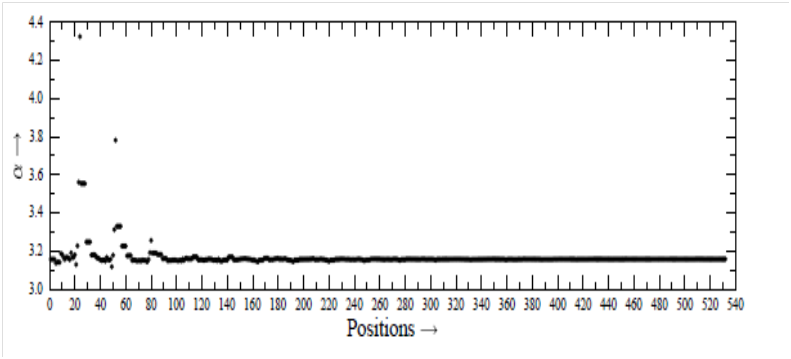
Figure 2 Values of $\alpha$  for various positions. We have r =2 (0.25) 6.5 Å. Each r has 28 positions.

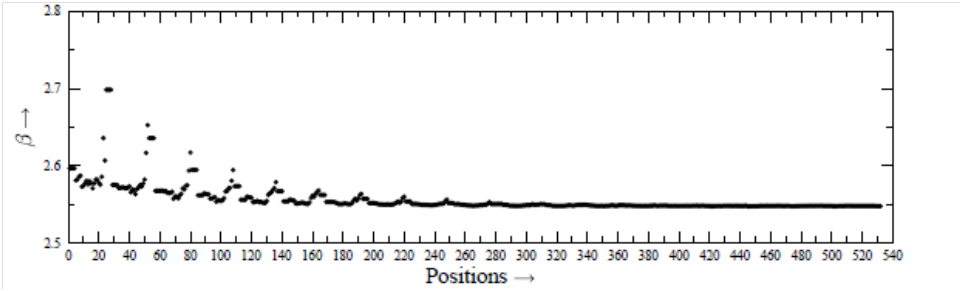
Figure 3 Values of $\beta$ for various positions. We have r=2 (0.25) 6.5 Å. Each r has 28 positions.

For very large r, the α and β attain the limiting values, denoted by α₀ and β₀. The limiting values are α₀=3.157 and β₀=2.548, which can also be obtained with the help of the statistical methods and are used by the scientists. For small r, the deviations of α and β with respect to α₀=3.157 and β₀=2.548, are very significant. With the increase of r, the deviations decrease. Using the constant values α₀ = 3.157 and β₀=2.548, we have calculated the total energy E₀ at each position. For the values of α and β at each position, we have calculated total energy E, and plotted in Figure 4, the value of (E−E₀) as a function of position. The values of (E−E₀) are found to have the value up to the order of 10⁻² atomic unit (A U). The deviations shown in Figure 4 are quite significant, in particular for the small value of r, as the total energy is generally calculated up to the accuracy of 10⁻⁸ A U. Finally, by using these values of α and β at each position, the HF (reference energy) and the energy of correlations, and finally the total energy, corresponding to n=∞, can be calculated, and very accurate PES can be generated.^19–23

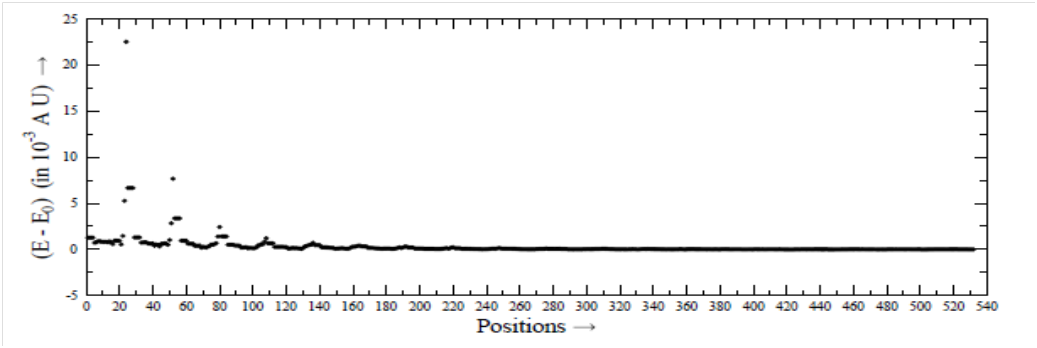
Figure 4 Values of (E−E0) for various positions. We have r = 2 (0.25) 6.5 Å. Each r has 28 positions.

Using the best method, CCSD (T) and three basis-sets, aug-cc-pVDZ, aug-cc-pVTZ, aug-cc-pVQZ, separately, we have calculated energies for H2CS-He system. We have shown that the exponents α and β used for the basis-set extrapolation are not constant, but vary from position to position in the system. The deviations of α and β are very significant for low values of r. For very large r, α and β approach to the constant values α₀ and β₀. Finally, we have calculated the deviations of energy E corresponding to the α and β from the energy E0 corresponding to the α0 and β₀. The values of (E−E₀) is of the order of 10⁻² A U, while the energies are generally calculated up to the accuracy of 10⁻⁸ A U. Thus, the α and β cannot be taken as constant.

None.

1. Daniel F, Faure A, Wiesenfeld L, et al. Collisional excitation of singly deuterated ammonia NH₂D by H₂. MNRAS. 2014;444:2544–2554.
2. Dumouchel F, Faure A, Lique F. The rotational excitation of HCN and HNC by He: temperature dependence of the collisional rate coefficients. MNRAS. 2010;406(4):2488–2492.
3. Faure A, Wiesenfeld L, Scribano Y, et al. Rotational excitation of mono- and doubly-deuterated water by hydrogen molecules. MNRAS. 2012;420(1):699–704.
4. Flower DR, Lique F. Excitation of the hyperfine levels of ¹³CN and C¹⁵N in collisions with H₂ at low temperatures. MNRAS. 2015;446(2):1750–1755.
5. Gotoum N, Nkem C, Hammami K, et al. Rotational excitation of aluminium monofluoride (AlF) by He atom at low temperature. Astr Space Sci. 2011;332(1):209–217.
6. Machin L, Roueff E. Collisional excitation of monodeuterated ammonia NH₂D by helium. A&A. 2006;460(3):953–958.
7. Machin L, Roueff E. Collisional excitation of doubly deuterated ammonia ND₂H by helium. A&A. 2007;465(2):647–650.
8. Pople JA, Head-Gordon M, Raghavachari K. Quadratic configuration interaction. A general technique for determining electron correlation energies. J Chem Phys. 1987;87(10):5968.
9. Truhlar DG. Basis-set extrapolation. Chem Phys Lett. 1998;294(1-3):45–48.
10. Wheeler MD, Ellis AM. A new potential energy surface for He–H2CO. Chem Phys Lett. 2003;3(4):392–399.
11. Sinclair MW, Fourikis N, Ribes JC, et al. Detection of Interstellar Thioformaldehyde. Austral J Phys. 1973;26:85–92.
12. Sarrasin E, Abdallah DB, Wernli M, et al. The rotational excitation of HCN and HNC by He: new insights on the HCN/HNC abundance ratio in molecular clouds. MNRAS. 2010;404(1):518–526.
13. Pottage JT, Flower DR, Davis SL. The rotational excitation of methanol by para-hydrogen. MNRAS. 2004;352(1):39–43.
14. Rabli D, Flower DR. The rotational structure of methanol and its excitation by helium. MNRAS. 2010a;403(10):2033–2040.
15. Rabli D, Flower DR. The rotational excitation of methanol by molecular hydrogen. MNRAS. 2010b;406(1):95–101.
16. Rabli D, Flower DR. Rotationally and torsionally inelastic scattering of methanol on helium. MNRAS. 2011;411(3):2093–2098.
17. Sharma M, Sharma MK, Verma UP, et al. Collisional rates for rotational transitions in H2CO and their application. Adv Space Res. 2014a;54(2):252–260.
18. Sharma MK, Sharma M, Verma UP, et al. Collisional excitation of vinylidene (H₂CC). Adv Space Res. 2014b;54(9):1963–1971.
19. Sharma MK, Sharma M, Verma UP, et al. Radiative transfer in silylidene. Serb Astron J. 2014c;188:37.
20. Sharma MK, Sharma M, Verma UP, et al. Collisional excitation of thioformaldehyde and silylidene. Adv Space Res. 2015;55(1):434–439.
21. Troscompt N, Faure A, Wiesenfeld L, et al. Rotational excitation of formaldehyde by hydrogen molecules: ortho-H2CO at low temperature. A&A. 2009;493(2):687–696.
22. Wernli M, Wiesenfeld L, Faure A, et al. Collisional excitation of sulfur dioxide in cold molecular clouds. A&A. 2007a;464:1147.
23. Wernli M, Wiesenfeld L, Faure A, et al. Rotational excitation of HC₃N by H₂ and He at low temperatures. A&A. 2007b;464(3):1147–1154.