Difficulties of the analytical approach to a solution of the problem of acoustic radiation transfer through the outdoor atmosphere call for the application of numerical methods, from which the most promising, in our opinion, is the method of statistical simulation (Monte Carlo). This method allows sound scattering on refractive index fluctuations caused by wind and temperature in homogeneities to be correctly taken into account for the most realistic models of the propagation medium and geometrical parameters of the problem to be solved. A review of authors’ works devoted to the application of the Monte Carlo method to a solution of the problem of acoustic radiation transfer through the lower 500-meter layer of the plain-stratified turbulent atmosphere is presented in the report. The acoustic model of the atmosphere is considered, and the structure and special features of the computational algorithm of the Monte Carlo method are discussed. The influence of the outer scale of atmospheric turbulence on the distribution of the transmitted acoustic radiation intensity is investigated for sound frequencies in the range 1–4 kHz. Regional and seasonal variations of the contribution of multiple scattering to the transmitted radiation intensity as well as the effect of cloudiness and source altitude are investigated. The calculated dependences of the transmitted acoustic radiation intensity and of the multiple scattering contributions on the angle of source divergence and source altitude above the Earth’s surface are discussed. Calculations were performed for a point sound source and a source with circular aperture and uniform and Gaussian radiation distributions. Good agreement of calculated values of the total sound attenuation with the available experimental data confirms the reliability of the results of statistical simulation. PACS: 43.28.-g; 43.28.+h

Keywords: atmospheric acoustics, monte-carlo method, statistical simulation, acoustic radiation transfer

Investigations of sound propagation in the atmosphere are necessary for its prediction, finding direction to a sound source, and quantitative interpretation of results of acoustic sounding.¹ In the outdoor atmosphere, the sound propagation is influenced by a great number of factors, the main of which are the vertical atmospheric stratification, viscosity, turbulence, and angular beam divergence. Difficulties of analytical approach call for the application of numerical methods from which,^2,3 by our opinion, the Monte Carlo method first used in⁴ for statistical estimation of the multiple scattering contribution to the distribution of the transmitted acoustic radiation intensity over detector zones depending on the sound frequency and outer scale of atmospheric turbulence is most promising. This method allows sound scattering on the acoustic refractive index fluctuations caused by wind velocity and temperature in homogeneities to be taken into account for the most realistic models of the atmosphere and concrete geometry of numerical experiment.

The main results obtained by the authors can be found in.^4–11 Calculations by the Monte Carlo method were performed for the acoustic model of the atmosphere based on the theoretical estimates of sound scattering by the atmospheric turbulence presented in¹² for the von Karman model of the spectra of atmospheric temperature and wind velocity fluctuations. In calculations of the vertical profiles of the acoustic absorption and scattering coefficients, the vertical profiles of the atmospheric temperature, pressure, and sound velocity were taken from the standard model of the mid-latitude summer atmosphere. Both conventional computational procedures¹³ and procedures developed in^6,14,15 with allowance for the specifics of the interaction of sound with the atmosphere were used. The flow chart of the computational algorithm was presented in.¹⁰ Calculations were performed for a point source with coordinates $x= 0,y = 0,z = H_s$ , where$0\le H_s\le 35 m$ , and a source with circular aperture 1 m in diameter and power of 1 W, sound frequencies $1000 Hz \le F \le 4000 Hz$ , and the outer scale of atmospheric turbulence L₀=10–100 m. The angle of source divergence was$\varphi = 2.5–25°$ . The receiver was placed at an altitude of 500 m. The radiation distribution over the horizontal plane of the detector depending on the distance Нfrom the vertical axis passing through the source (over the detector zones with H =10–100 m with a step of 10 m and then with a step of 50 m to H =500 m) was estimated with allowance for the contribution of multiply scattered radiation. The acoustic radiation of the source propagated through the plane-parallel atmospheric layers with constant within these layers coefficients of classical,${\sigma }_{\text{cl}}\left(j\right)$ and molecular absorption, ${\sigma }_{\text{mol}}\left(j\right)$ and scattering on turbulent fluctuations of the temperature,${\sigma }_T\left(j\right)$ and wind velocity,${\sigma }_V\left(j\right)$  where$j=1,\dots ,25$ . The 500-meter plain-stratified turbulent atmosphere was subdivided into 25 layers 20 m each. Calculations were performed on a personal computer for 10⁶–10⁷ phonon histories that provided error in the range 3–10%. Time of calculating the individual realization did not exceed 15 min.

As an example, Figure 1 shows the altitude dependence of the total attenuation coefficient ${\sigma }_{\text{att}}\left(j\right)={\sigma }_{\text{cl}}\left(j\right)+{\sigma }_{\text{mol}}\left(j\right)+{\sigma }_T\left(j\right)+{\sigma }_V\left(j\right)$  for frequencies in the range 1000-4000 Hz and outer scale of turbulence L0 = 80 m (a) and the phonon scattering probability$P_{sc}\left(j\right)=\left[{\sigma }_T\left(j\right)+{\sigma }_V\left(j\right)\right]/{\sigma }_{\text{att}}\left(j\right)$  (b). Results of calculations demonstrated that for a frequency of 2 kHz, most often used in sodars, the turbulent attenuation becomes comparable with the molecular absorption in the surface layer of the atmosphere already for L0 = 15 m ($P_{sc} \ge 0.5$ ). For L0 = 80 m, $P_{sc }> 0.56$ in the examined frequency range (Figure 1). In the surface layer, the total attenuation coefficient increases approximately by an order of magnitude when L₀ increases from 10 to 80 m.

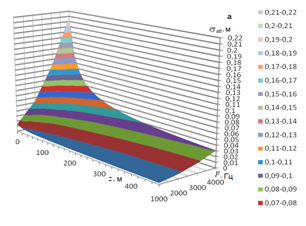
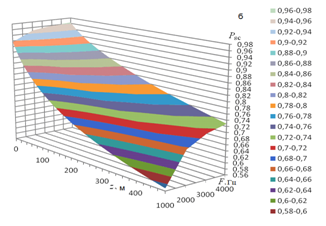
Figure 1 Altitude dependence of the total sound attenuation coefficient (a) and phonon survival probability (b) for frequencies F=1000–4000 Hz and outer scale of turbulence L₀=80 m.

Figure 2 shows the normalized phase functions of sound scattering on temperature (a) and wind velocity fluctuations (b). Results of calculations demonstrated that their elongation in the forward direction increases with the outer scale of turbulence. Thus, the portion of radiation scattered in the forward direction increases by a factor of 15 when L₀ increases from 10 to 40 m; it increases by a factor of 63 for L₀=80 m. it should also be noted that good agreement of the calculated coefficients and scattering phase functions with the available experimental data was demonstrated.¹²

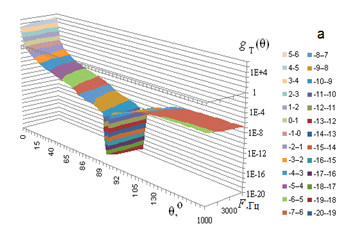
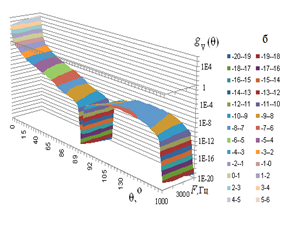
Figure 2 Normalized phase functions of sound scattering on temperature (a) and wind velocity fluctuations (b) for frequencies F =1000–4000 Hz and outer scale of turbulence L₀ = 80 m.

Results of calculations by the Monte Carlo method of the total attenuation of acoustic radiation, in dB, for vertical sound propagation at frequencies of 2800 Hz (the dashed curve) and 4000 Hz (the solid curve) are shown in Figure 3. Symbols here show the results of measurements¹⁶ with a tethered balloon. Good agreement of the results of our calculations by the Monte Carlo method with the experimental data can be seen, which confirms the efficiency of the suggested computational algorithm.

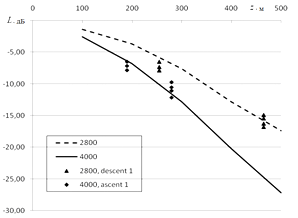
Figure 3Total sound attenuation for its vertical propagation. Here the dashed curve shows the results of calculations by the Monte Carlo method and closed triangles show the data measured¹³ with the ascending tethered balloon at F =2800 Hz; the solid curve shows the results of our calculations and closed diamonds show the data measured¹³ with the descending tethered balloon at F =4000 Hz.

The influence of the source aperture and the form of radiation distribution is illustrated by Figure 4 which shows the distributions of the transmitted (I_tr) and multiply scattered (I_msc) radiation intensities, in W/m², over the detector zones for the point sound source and the source with the circular aperture 1 m in diameter and uniform and Gaussian radiation distributions over the source aperture for F=3000 Hz,$\varphi = 2.5°$ , and L0=10 m. From the figure it can be seen that the intensity of transmitted radiation in the first detector zone I_tr ($0°, 2.5°$ ) increases by 66–68% for the source with the circular aperture and Gaussian radiation distribution in comparison with the point source. For the source with the circular aperture and uniform radiation distribution, it remains almost unchanged.

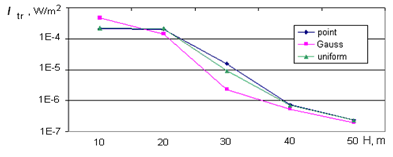
Figure 4 Distributions of the intensity of transmitted (I_tr) and multiply scattered (I_msc) acoustic radiation over the detector zones for the point source and the source with circular aperture and uniform and Gaussian radiation distributions over the source aperture.

Figure 5 from¹⁰ shows the dependence of the distribution of transmitted and multiply scattered radiation over the detector zones for frequencies of 1.7 and 4 kHz and angles of source divergence $\varphi = 5$  and 15°. Results of calculations demonstrate that for F=1.7 kHz, the contribution of multiple scattering to the transmitted radiation intensity increases with the outer scale from ~10% for L₀=10 m to ~90% for L₀=60 m; for L₀=80 m, the transmitted radiation intensity is almost completely determined by the contribution of multiple scattering. In this case, the sharp decrease of Itr is caused by the exit from the source radiation cone.

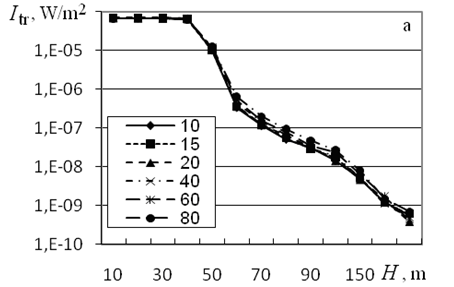
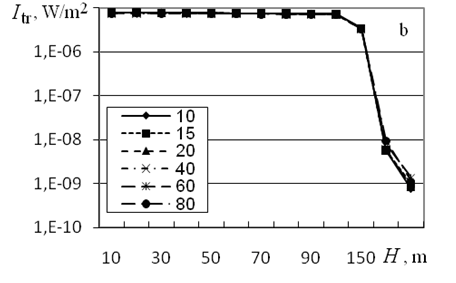
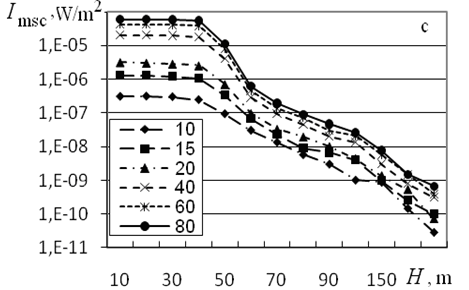
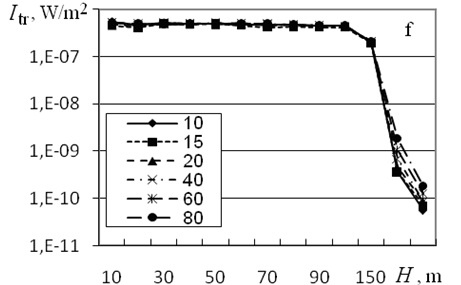
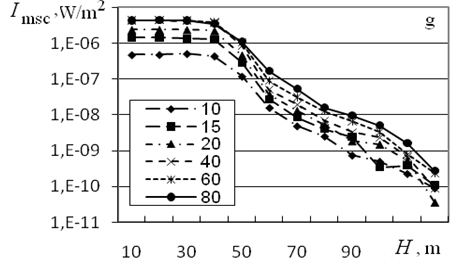
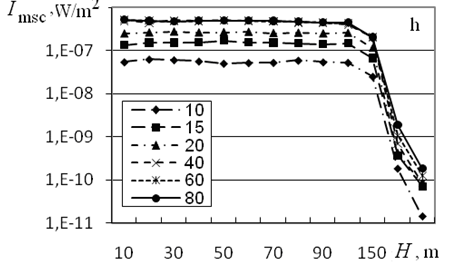
Figure 5 Distributions of the transmitted (I_tr, W/m²) and multiply scattered radiation intensity (I_msc, W/m²) over the detector zones for F =1.7 kHz, $\varphi = 5$ (a and c) and 15 (b and d); F = 4 kHz, $\varphi = 5$ (e and g) and 15 (f and h) and indicated values of the outer scale of turbulence, in meters.

The contribution of multiple scattering within the source radiation cone increases from 4.7×10^–7 to 4.3×10^–6 W/m², that is, by 89% when L₀ increases from 10 to 80 m. This increase in the multiple scattering contributions compensates for the corresponding decrease of the transmitted radiation intensity due to the increase in the outer scale of turbulence and, as can be seen from Figure 5A, I_tr for $H< 50$ m remains virtually independent of L₀.

The dependence of the transmitted radiation intensity for the first detector zone on the angle of source divergence is well described by a quadratic power-law dependence:$I_{tr}(0°,\varphi ) = A\times {\varphi }^{–2}$ , where $I_{tr}$  is in W/m² and $\varphi$  is in degrees. Thus, for F=1000, 2000, 3000 and 4000 Hz, A =2.8×10^–3, 1.4×10^–3, 2×10^–5 and 4×10^–6, respectively. When the angle of source divergence increases from 5 to 25°,$I_{tr}$ decreases by 96%, which confirms the necessity of application of massive protective shields in sodars.

Figure 6 from⁵ shows the calculated dependences of the multiple scattering contribution (I,%) to the transmitted radiation intensity for the first detector zone with radius H=10 m on the source altitude H_s for L₀=10 Figure 6(A) and 20 m Figure 6(B). Sound frequencies F are plotted on the y axis. From the figure it can be seen that the multiple scattering contribution essentially decreases as the source altitude increases from 5 to 20 m. With further increase in the source altitude, it changes only slightly. Therefore, the source altitude Н_s=20 m can be recommended as optimal for acoustic sounding taking into account that the multiply scattered signal represents noise in the interpretation of the data of acoustic sounding.

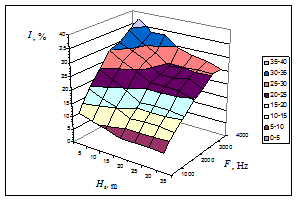
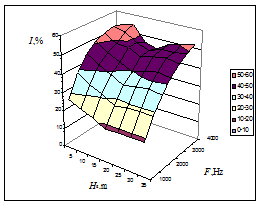
A                                          B

Figure 6 Dependence of the multiple scattering contribution to the transmitted radiation intensity on the source altitude H_s above the Earth’s surface for L₀ =10 (A) and 20 m (B).

The influence of cloudiness is illustrated by Figure 7 which shows statistical estimates of the multiple scattering contribution, MRS, in %, to the transmitted radiation intensity for frequencies in the range 500–3000 Hz in clear and cloudy winter days (for the average relative surface air humidity in winter u = 67 and 81%.17

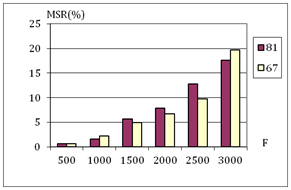
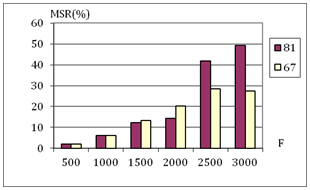
A                                          B

Figure 7 Contribution of multiple scattering to the transmitted acoustic radiation intensity in the first detector zone in clear and cloudy days for H_s = 35 m and L₀ =10 (A) and 20 m (B).

From the figure it can be seen that for L₀=20 m and sound frequency of 3000 Hz, variations of the multiple scattering contribution caused by cloudiness are ~20%; moreover, the contribution of multiple scattering increases in cloudy days. To investigate seasonal variations of the multiple scattering contribution, calculations were performed with summer¹⁸ and winter^17,19 standard mid-latitude models of the atmosphere. Results of calculations are shown in Figure 8.⁸

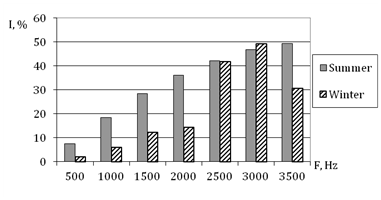
Figure 8 Seasonal (winter-summer) variability of the multiple scattering contribution to the transmitted radiation intensity for the first detector zone, H_s =35 m, and L₀ =20 m.

From the figure it can be seen that in summer for L₀=20 m the contribution of multiple scattering to the transmitted radiation intensity is by 4–17% larger than in winter. In addition, the seasonal dependence is complex in character. For larger L₀ values, the seasonal dependence is intensified. For L₀=5 m, the difference does not exceed 4%; for L₀=10 m, it is 10% for the acoustic frequency F=2500 Hz; and for L₀=20 m, it reaches 17%.

Statistical estimates of the regional variability of the multiple scattering contributions were obtained for Moscow and Novosibirsk. It was established that in winter for L₀=20 m and F=3000 Hz, the contribution of multiple scattering for the first detector zone was 34% for Moscow and 50% for Novosibirsk, which demonstrates its essential regional variability.

Results were obtained with support under Project No. 5.3279.2017/PSN of the Assignment of the Ministry of Education and Science of the Russian Federation and under the Project No. IX.138.2.5 of the Program of Basic Research of the Siberian Branch of the Russian Academy of Sciences.

Authors declare there is no conflict of interest.

1. Krasnenko NP. Acoustic sounding of the atmospheric boundary layer. Russia: Publishing House “Vodolei”; 2001. 278 p.
2. Golitsyn GS, Romanova NN. Vertical propagation of sound waves in the atmosphere with the altitude-dependent viscosity. Izvestiya Akademii Nauk Sssr Seriya Fizicheskaya. 1968;4(2):118–120.
3. Matuschek R, Mellert V, Kephalopoulos S. Model calculations with a fast field programme and comparison with selected procedures to calculate road traffic noise propagation under definite meteorological conditions. Acta Acustica United with Acustica. 2009;95(5):941–949.
4. Baikalova RA, Krekov GM, Shamanaeva LG. Statistical estimates of multiple scattering contributions for sound propagation in the atmosphere. Atmospheric and Ocean Optics. 1988;1(5):25–30.
5. Shamanaeva LG, Burkatovskaya YB. Statistical estimates of multiple scattering contributions to the intensity of acoustic radiation transmitted through the lower 500-meter layer of the atmosphere. Russian Physics Journal. 2004;2:71–76.
6. Shamanaeva LG, Burkatovskaya YB. Study of multiple scattering effects on the acoustic wave propagation through a turbulent atmosphere. In: Anderson P, Bradley S, et al. editors. UK: Proceeding 12th International Symposium on Acoustic Remote Sensing and Associated Techniques of the Atmosphere and Oceans; 2004:145–148.
7. Shamanaeva L, Burkatovskaya Y. Statistical estimates of the multiple scattering contributions to the transmitted acoustic radiation intensity. International Symposium for the Advancement of Boundary Layer Remote Sensing. In: Emeis S, editor. Germany; 2006:14–16.
8. Shamanaeva LG, Burkatovskaya YB. Variations of the multiple scattering contribution to the transmitted acoustic radiation intensity. Russian Physics Journal. 2007;50(10):1056–1060.
9. Belov VV, Burkatovskaya YB, Krasnenko NP, et al. Statistical estimates of the influence of the source divergence angle on the characteristics of transmitted acoustic radiation. Russian Physics Journal. 2009;12:14–19.
10. Belov VV, Burkatovskaya YB, Krasnenko NP, et al. Influence of the width of the source directivity pattern on the characteristics of transmitted acoustic radiation. Russia: Materials of XVI International Symposium “Atmospheric and Ocean Optics. Atmospheric physics”; 2009:142–146.
11. Belov VV, Burkatovskaya YB, Krasnenko NP, et al. Statistical estimates of influence of the angular beam divergence on the characteristics of acoustic radiation transmitted through the atmosphere. France: 15th International Symposium for the Advancement of Boundary Layer Remote Sensing; 2010.
12. Baikalova RA, Krekov GM, Shamanaeva LG. Theoretical estimates of sound scattering by atmospheric teurblence. The Journal of the Acoustical Society of America.1988;83(4):1332–1335.
13. Marchuk GI, Mikhailov GA, Nazaraliev MA, et al. Monte Carlo method in atmospheric optics. Russia: Nauka; 1976.
14. Krekov GM, Shamanaeva LG. Statistical estimates of the spectral brightness of the Earth’s twilight atmosphere. Russia: Nauka; 1974:180–186.
15. Krekov GM, S’edin VY, Shamanaeva LG. Application of the Monte Carlo method to problems of acoustic radiation transfer in the atmosphere. Russia: VIII All-Union Symposium on Laser and Acoustic Sounding of the Atmosphere; 1984:176–181.
16. Aubry M, Baudin F, Weil A, et al. Measurements of the total attenuation of acoustic waves in the turbulent atmosphere. Journal of Geophysical Research. 1974;79:5598–5606.
17. Matveev LT. Course in general meteorology. Russia: Gidrometeoizdat; 1984. 151 p.
18. Glagolev YA. Handbook on the physical parameters of the atmosphere. Russia: Gidrometeoizdat; 1984:68–70.
19. Komarov VS, Kreminskii AV, Sineva KY. Computer information base of regional climatic models of the temperature and wind velocity for the atmospheric boundary layer. Atmospheric and Ocean Optics. 1996;9(4):484–488.