We analyzed coronal mass ejection (CME) observed parameters, sunspot number (SSN) and sunspot area (SSA) for solar cycle 23, comparing them to check for possible similarities in their variation pattern within the solar cycle. In general, most of the CME parameters (including the number of yearly occurrence, the angular width, speed parameters, mass, estimated force and kinetic energy) increase/decrease in values as the sunspot number and sunspot area increase/decrease in values. Between 2000 and 2002, we observed a peak–dip–peak (the double–hump pattern) in the SSN and SSA, similar double–humped pattern were also observed in most of the CME parameters but occurring at a later time. Dividing the solar cycle into period of increasing solar activity (which we termed the ascending phase–1996 to 2002) and decreasing solar activity (which we termed the descending phase–2002 to 2008) showed that the correlation between some of the coronal mass ejection and sunspot parameters differs during the ascending and descending phases.

Keywords: CME, general–sunspot, general–method, data analysis

CME, coronal mass ejection; SSN, sunspot numbers; SSA, sunspot area; LASCO, large angle and spectrometric coronagraph; SOHO, solar and heliospheric observatory; SSANH, sunspot area in northern hemisphere; SSASH, sunspot area in southern hemisphere; KE, kinetic energy.

Coronal Mass Ejection (CME) constitutes large–scale ejections of mass and magnetic flux from the lower corona into the interplanetary medium.¹ It is recognized to be the most spectacular form of solar activity and perhaps the primary driver and source of space weather.² A classical CME carries away some1014–1017g of coronal mass and can liberate energies of the order 1022–1025J.^3–5 In broad band white–light corona graphic images, CMEs are seen as bright features moving radially outward. A plausible important cause behind the generation of CME is magnetic reconnection.^6–10 When two oppositely charged magnetic fields are brought together, rearrangement takes place and immediately after this rearrangement, the energy stored in the oppositely directed magnetic field lines are released.^3,11–13 This sudden release of energy is assumed responsible for solar flares which drives the CME (Aoki, Yashiro & Shibata 2003; Reinard 2008). The association of solar flare and CME has been studied by many authors such as.^11,12 The strength of the magnetic field is stronger at the active regions of the Sun from where the solar flares and CMEs are believed to originate from, Carrington¹⁴ & Hodgson¹⁵ noted that solar flares, especially the larger ones, are known to appear in and around active regions including sunspots.

Sunspots are actually massive solar storms that are difficult to predict.^16,17 When a sunspot occurs, it carries with it the magnetic current brake, forming areas of reduced surface temperature.^18–20 Their numbers, covered area and intensity vary. These variations in number density shows a cyclic period of approximately 11 years called the solar cycle. The solar cycle is been tracked by counting sunspots. Of all solar activity features, the sunspots are the most easily observed and have been tracked since around early 1600s.^17,21–25 The sunspots may appear as single, isolated umbra (the dark central region) surrounded by a symmetric penumbra (less dark pattern surrounding umbra) or they may appear in groups.²⁶ Central to the occurrence of the 11–year cycle is the oscillating magnetic dynamo within the Sun.^27–32 Sunspot cycles are observed to vary both in size and length; therefore, it is difficult to describe the shape of sunspot cycles with a universal function.^33,34 Plethora of literatures is available where the authors have attempted to describe the cycles as a periodic phenomenon.^{27–29,31,32}

The variations in the rate of occurrence of CMEs and associated observational physical parameters have been studied using the Large Angle Spectrometric Coronagraph (LASCO) CME data.^35–38 The observed approximately 11–year solar cycle and solar rotation modulate the evolution of magnetic flux of the Sun,^3,39 thus different observed physical quantities related to a measure of solar activity should be well correlated⁴⁰ such as CME parameters, sunspot numbers (SSN), sunspot area (SSA), solar flares, solar radio bursts and solar prominences. According to Low⁴¹ CMEs create large–scale changes in the corona, which have fundamental implications for the evolution of the magnetic flux of the Sun that is ultimately related to the solar dynamo.^39,42 Therefore, it is reasonable to expect a good correlation between the various observed physical parameters of CMEs and the other tracers of solar activity such as sunspots number and sunspots areas.⁴⁰

Understanding the variations in the measure of solar–activity–cycle parameters remains a key unsolved problem in the solar physics. It is both an outstanding theoretical problem and an important practical issue, since solar activity and the related output radiation influence on the biosphere, space weather and technology on the Earth.^43-45 It has been postulated that the irregular dynamics of the solar cycle may embed chaotic process,^20,46–48 making it difficult to predict solar activity.⁴⁹ However, several authors have reported that the time evolution of different the solar activity parameters does not match together exactly, which had been attributed to the complicated dynamics involved at different depths in the solar atmosphere.¹⁶ Gopalswamy et al.³⁷ reported on the mismatch between the peak occurrence of the halo CME rate and the SSN during the solar cycle 23, where the maximum halo CME rate occurred two years after the peak occurrence of SSN. In studies done by Ramesh & Rohini⁵⁰ it has been noted that the sunspot areas (SSAs) better represent the solar cycle than the SSN.

In this context, we examine here the observed characteristics of CMEs such as angular width, linear speed, final speed, speed at radius as 20 times as the solar radius, acceleration, estimated force (F estimated from the observed mass and absolute acceleration reported by Gopalswamy⁵¹. It should be noted that CMEs believed to originate from the solar active regions,^52–54 are subjected to propelling and retarding force leading to changes in speed, kinetic energy and position angles in association with the sunspot area both in the Southern and Northern Hemispheres and sunspot numbers. Section 1 is the introduction. In Section 2, we describe the parameters in the data, their sources and the way of analysis. The results are discussed in Section 3. In Section 4, we summarize and conclude.

The CME data used in this study is collected from the Large Angle and Spectrometric Coronagraph (LASCO) onboard the Solar and Heliospheric Observatory (SOHO) available in CME catalogue that can be found at http://cdaw.gsfc.NASA.gov/CME.⁵⁵ LASCO CME catalog contains list of all CMEs manually identified from 1996 onward from the LASCO onboard the SOHO mission with gaps in collected data. These data gaps occurred (i) in 1998 from 24 June to 22 October, (ii) failure of all three gyroscopes caused an interruption from 21 December 1998 to 6 February 1999 and (iii) in June 2003, the problem was overcome and nominal observations resumed on July 10. The catalog contains the observed CME parameters including Angular Width (AW is the angular measure of the size of the CME in the LASCO image) in degrees, Linear Speed (LS) in km/s, Final Speed (FiS) in km/s, Speed at radius as 20 times as the solar radius (20R) in km/s, acceleration (A) in km/s², Kinetic Energy (KE) in J and Position Angles (Central Position Angle/Meridian Position Angle–CPA/MPA; The MPA gives the position angle at which the height–time measurements are made; while the CPA is essentially used to distinguish CMEs appearing simultaneously in the LASCO field of view, thus ideally the CPA and MPA are the same) in degrees. We also calculated the estimated 'force' (F in N) from the observed mass and the absolute value of the observed acceleration.

The solar cycle 23 was started in June 1996 and ended in March 2008. We selected the CME data spanning from January 1996 to December 2008 (this included the ending of the solar cycle 22 and the beginning of the solar cycle 24). There are about 14000 CMEs within this period. Since our analysis involves average monthly and yearly values, being at low solar activities that may not really impact our results. We first calculated the weekly average from the observed daily values. We calculated the monthly and yearly averages which we used in our analysis.

The data for the sunspot number and area analyses were extracted from the OMNI Web Service archive from NASA Space Physics Data Facility for the year 1755 to 2008 using the total monthly sunspot number. The monthly data with the sunspot area (for the Northern Hemisphere, Southern Hemisphere and the total solar surfaces) were extracted for the solar cycle 23 (January 1996 to December 2008).

In Figure 1&2, we show the plot of the number of yearly occurrence of CME events (NOC), the yearly total sunspot number (SSN), the sunspot area for the Northern Hemisphere (SSANH), Southern Hemisphere (SSASH), and the Total Sunspot Area (SSAT) estimated by summing the sunspot areas in both Southern and Northern Hemisphere. The plot showed an increase from about 200 CME events in the year 1996 to a maximum (about 1500 to 1700 CME events) between the year 2000 to 2002 slight dip in the year 2001, then a reduction from the peak values between 2003–2008 (with CME NOC hovering between 1200–800 CME events, except in 2007 when it rose to about 1400 CME events) (Table 1). Kilcik et al.,⁵⁶ obtained similar result. For the SSN, a peak was reached in the year 2000 with a steady decline from 2001 to 2008.

Figure 1 The number of occurrence of CME per year (NOC), sunspot number (SSN).

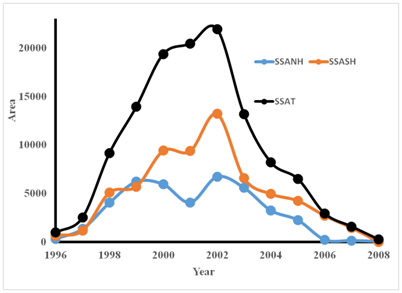
Figure 2 The yearly average time series plot of Sunspot Area (SSAT (Total)), SSANH (Northern Hemisphere) and SSASH (Southern Hemisphere)) for the solar cycle 23.

For the time series plot of Total Sunspot Area (SSAT), a peak was observed in 2002, similar for that of Southern Hemisphere sunspot area (SSASH). For the time series plot of sunspot area in the Northern Hemisphere (SSANH), the trend in variation indicates peaks in 2000 and 2002 with a slight dip in 2001 (similar to the double–hump–peak–dip–peak reported by Ramesh⁴⁰ & Kilcik et al.,⁵⁶ with a steady decline from 2003 to 2008.

In Table 2, the average yearly values of the CME parameters (MPA, AW, LS, FiS, 20R, A, M, F and KE), and the total yearly number of occurrence of CME were shown, while in Figures 3–12, we display the time series plot of observed monthly averages of the CME parameters, overlaid with the 12–month average. For the CPA/MPA, apart from few outliers above 210 deg, the observed monthly average lies between 140–210 deg, and from Table 2, the yearly averages ranges from 176.0–189.1 deg (a difference of about 13 deg), indicating that the yearly average of the position angle is constant. The AW variation seems to suggest an increase as the solar activity increases as well as a decrease with decreasing the solar activity, slightly reaching a peak during the year 2001 (see the overlaid yearly average).

The speed parameters (LS, FiS and 20R) seem to follow the sunspot number yearly variation, increasing from 1998 and reaching at peak generally in 2003, before steadily decline to 2008. The average monthly linear speed (LS) ranges from about 150 km/s to about 850 km/s with a mean of $\sim 400 \pm 100km/s$ . LS seems to increase with periods of increase in the solar activity, maintaining a high average values between 1999 to about mid 2005 before a gradual decrease till 2008 which is during solar minima but with a slight peak in the yearly average in 2004. The average monthly FiS ranges from 176 km/s to 825 km/s with a mean of $\sim 413 \pm 88km/s$ and showed similarity to the trend in the variation of LS, again with a slight peak in the year 2004. The yearly average of speed at 20R ranges from 116 km/s to 824 km/s with a mean of $464 \pm 74km/s$ . The trend in its variation from the overlaid yearly variation indicates that it increased steadily from 1996 to about the end of 1998, remained generally constant till about 2004, reached at peak, decreased slightly in early 2005, and reached at peak again about in the middle of 2005, before decreasing steadily towards the end of the solar cycle 23 in 2008.

The variation in the acceleration seems to suggest that CMEs have average positive acceleration towards and during the solar minimum, but average negative acceleration towards the solar maximum. For the acceleration, it seems that at the start and end of the solar cycle (during minimal solar activity), the overlaid yearly average tends towards positive acceleration while during the middle of the period (higher solar activity), the yearly average of the acceleration tends towards negative values.

The general observation suggests masses and the estimated forces (F) of CMEs increase during the solar maximum but seem to decrease towards the solar minimum. The yearly average KE increases from low values during the beginning of the solar cycle (solar minimum), oscillates with the solar cycle and then decreases toward the end of the solar cycle (another solar minimum). The monthly average mass ranges from$~1.9x{10}^{14}- 4.5x{10}^{15}g$ with a mean value of $1.2\pm 0.6x{10}^{15}g$ . The variation in the observed monthly averages of mass from the overlaid yearly trend showed an increase from the solar minimum in 1996 to about 1998, then decrease in value till 1999, before another increase till about mid–2002, then a steady decrease (though with little increase at about 2005) till 2008 towards the end of the solar cycle. The monthly average of the estimated force ranges from $~2.1x{10}^{12}- 1.4x{10}^{14}N$ , with a mean value of $2.4\pm 1.4x{10}^{13}N$ . The overlaid yearly average from monthly time series plot of estimated force indicates that F increased at the beginning of the solar cycle 23 (from 1996) up to some peak value in mid–1999, and begins to fluctuate in value between 1999 till around mid–2005, then gradually decreases till 2008 which is towards the end of the solar cycle 23. This suggests that F seems to increase during increase in the solar activity. The range of the average monthly KE is $~3.8x{10}^{21}-1.7x{10}^{24}J$ with a mean value of$1.8\pm 1.4x{10}^{23}J$ . In the time series plot of KE, the trend in the variation of the overlaid yearly average of the KE suggests that KE varies with the solar activity.

The trends in the variations of CME parameters (CPA/MPA, AW, LS, FiS 20R, M, A, F and KE) with SSN, SSAT and SSANH/SSASH for comparison are shown in Figure 3-12 (where we display the plots of normalized yearly average values of CME parameters, sunspot number and total sunspot area (normalized by dividing with the highest value of each parameter). The AW variations in general suggest increasing/decreasing angular width as sunspot number and sunspot area increases/decreases. The AW/SSA/SSAT plots also indicate that in 2000 during the peak of SSN/SSAT and SSANH/SSASH, AW dipped, while during the dip in 2001 in SSN/SSAT and SSANH/SSASH, AW reached at peak, followed by decrease till about October 2004, AW increased slightly, and at about September 2005, it decreases generally till 2008.

The peak–dip–peak (double hump:^37,40,51) followed by general decline in SSA/SSAT and SSANH/SSASH, between 2000 and 2002, is also observed in the speed parameters (LS and FiS), but with a delay in time. Whereas LS and FiS also peaked in 2000, we observe a dip in during mid–2002 and another slight peak during early 2004; for 20R, the peak–dip–peak occurred around September 2003 (peak)–October 20004 (dip)–September 2005 (peak), then the general decline till 2008.

Figure 3 Monthly time series plot of CPA/MPA (deg) for the solar cycle 23.

Figure 4 Monthly time series plot of CPA/MPA (deg) for the solar cycle 23.

Figure 5 Monthly time series plot of LS (km/s) for the solar cycle 23.

Figure 6 Monthly time series plot of FiS (km/s) for the solar cycle 23.

Figure 7 Monthly time series plot of 20R (km/s) for the solar cycle 23.

Figure 8 Monthly time series plot of A (m/s²) for the solar cycle 23.

Figure 9 Monthly time series plot of M(g) for the solar cycle 23.

Figure 10 Monthly time series plot of F(N) for the solar cycle 23.

Figure 11  Monthly time series plot of KE(J) for the solar cycle 23.

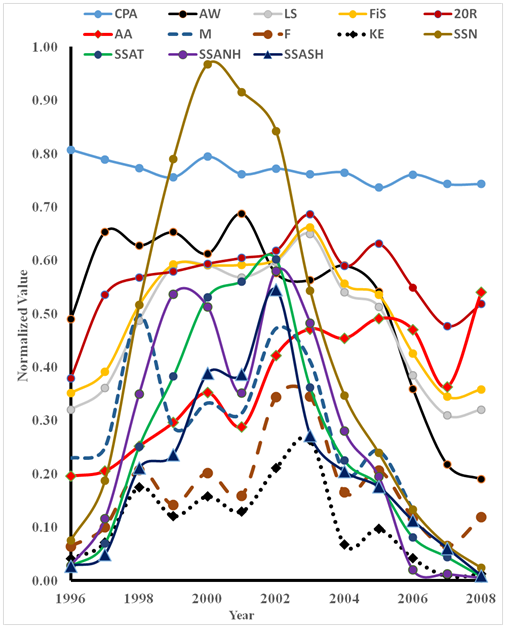
Figure 12  Normalized yearly averages time series plot of CME parameters (CPA/MPA, AW, LS, FiS, 20R, A, M, F KE) and sunspot parameters (SSN, SSAT, SSANH and SSASH) for the solar cycle 23.

For M, using the overlaid yearly average, aside the peak around June–July 1998 (which was followed by an 8 months period of gap in recorded data), another peak–dip–peak observed (similar to those observed in SSN/SSAT) and SSANH/SSASH, occurred around January 2002 (peak), March 2003 (dip) and November–December 2003 (peak). After general increasing from 1996 to 1998, the estimated force and the KE seem to show several peaks and dips from 1998 to 2005, then a general decline till 2008.

Regression analysis

The rate of solar activity generally increases during the beginning of each cycle, gets to a peak and then starts decreasing towards the end of the cycle. From Figure 1, using the sunspot number as an indicator of solar activity, decline in solar activity for the solar cycle 23 started in 2002 reached a peak in 2001 and started declining from 2002 to 2008. Thus to check for the variation in solar activity parameters, we divided the solar cycle 23 into period of increasing solar activity (January 1996 to December 2001–which we refer to as the ascending phase) and period of decreasing solar activity (January 2002 to December 2008–we call the descending phase). We compare the correlations between the CME parameters and sunspot parameters for the ascending phase, descending phase and the full solar cycle. The correlation coefficients are shown in Table 3 (r is the correlation coefficient and here is simply used to indicate the differences in the variation between the CME/Sunspot parameters in the ascending and descending phases).

Clearly, CPA/MPA does not show any kind of correlation neither with other CME parameters nor with sunspot parameters (SSN, SSAT, SSANH and SSASH) and there is no difference in the correlation between CPA/MPA with other CME and sunspot parameters for the whole solar cycle, for the increasing phase and the descending phase.

The correlation between AW and CME speed parameters (LS, FiS and 20R), M, F, KE, and the sunspot parameters seem stronger in the descending phase (period of decreasing) than in the ascending phase (period of increasing solar activity). AW also correlates positively with A during the ascending phase but negatively during the descending phase. In general, the speed parameters (LS, FiS and 20R) showed some form of positive correlation with AW, M, F, KE, SSN, SSAT, SSANH and SSASH which appear similar for the ascending and descending phases. LS and FiS seem to correlate negatively with A, which is stronger during the descending phase than during the ascending phase.

Acceleration shows some slight negative correlation with M, F, KE and the sunspot number and area parameters especially during the descending phase, but with lower correlation during the ascending phase. Mass of CME generally were correlated positively with F and KE as expected, and showed some positive correlation with the sunspot parameters which is stronger during the descending phase than during the ascending phase. The estimated force and KE were correlated with each other and fairly positively with the sunspot parameters. The strength of the correlation is slightly stronger for descending phase than the ascending phases. The sunspot parameters (SSN, SSAT, SSANH and SSASH) were correlated strongly with each other, but the values of the correlation results seem to suggest that the correlation is stronger during the descending phase than during the ascending phase.^57–67

We studied the trends in the variation of coronal mass ejection (CME) observational parameters (CPA/MPA, AW, LS, FiS, A, M, F and KE), sunspot number (SSN) and sunspot area (total area (SSAT), sunspot area in Northern Hemisphere (SSANH) and sunspot area in Southern Hemisphere (SSASH)) for the solar cycle 23. From the analysis, we note the following:

1. The Number of occurrence of CME (NOC) per year increases/decreases with increase/decrease in SSN/SSAT, but the variations is different.
2. SSASH is generally higher than those of SSANH.
3. The dip observed in the peak of NOC around 2002 also occurred in SSANH but not in SSASH.
4. Generally, we observed a peak–dip–peak period in both SSN and SSAT, which also seems to occur in some CME parameters–AW, LS, FiS, 20R and to some extent M, but with those of SSN/SSAT occurring earlier.
5. Between 1998 and 2005, when the solar activity increases, F and KE have high values, but with several peaks and dips.
6. The variations in SSANH and SSASH are similar and indicate peak–dip peak between 2002–2002.
7. The correlations between AW and the other CME parameters (LS, FiS, 20R, A, M, F, and KE) with the sunspot parameters (SSN, SSAT, SSANH and SSASH) appear to be stronger during the descending phase (DES) than the ascending phase (ASC).
8. There is no difference in the correlation between the CME speed parameters and the other CME parameters (except AW) with sunspot parameters during the ascending and the descending phase.
9. For A and M, the correlations between them and the other parameters appear to be stronger during the descending phase than during ascending phase; but there was no such difference in F and KE.
10. All the sunspot parameters showed strong correlations with each other but seems stronger during the descending phase than ascending phase

In conclusion, CME parameters and sunspot parameters indicates trends in the high solar activities for the solar cycle 23, but the variation differs for CME and sunspot parameters both in strength and period of variation. The most CME parameters generally show a time delay with sunspot parameters when reach at peaks. This is similar to the conclusion reached by Ramesh⁴⁰ and references therein. Moreover, we observed the double hump pattern in the most CME and sunspot parameters which have already been noted by several researchers.^40,50

The author wish to thank the referee whose invaluable contributions improved the quality of the article. The CME catalog used in this analysis is generated and maintained at the CDAW Data Center by NASA and The Catholic University of America in cooperation with the Naval Research Laboratory. SOHO is a project of international cooperation between ESA and NASA.

Author declares there is no conflict of interest.

1. Forbes TG. A review on the genesis of coronal mass ejections. Journal of Geophysical Research. 2000;105(10):23153‒23166.
2. Gosling JT. In Coronal Mass Ejections. USA: Geophysical Monograph Series; 1997.
3. Chen J. Coronal Mass Ejections: Models and Their Observational Basis. Living Rev Solar Physics. 2011;8:1.
4. Howard RA, Sheeley NR, Michels DJ, et al. Coronal mass ejections. Journal of Geophysical Research. 1985;90(1):8173‒8191.
5. Vourlidas A, Buzasi D, Howard RA, et al. In Solar Variability. USA. 2002;105:91‒94.
6. Chen J. Evidence of an Erupting Magnetic Flux Rope: LASCO Coronal. 1997;490:191.
7. Hundhausen AJ. In The Many Faces of the Sun. Germany: Springer; 1999. p. 143.
8. Wood BE, Karovska M, Chen J, et al. Comparison of Two Coronal Mass Ejections Observed by EIT and LASCO with a Model of an Erupting Magnetic Flux Rope. Astrophysical Journal. 1999;512(1):484‒495.
9. Chen J. Magnetic Geometry and Dynamics of the Fast Coronal Mass. Astrophysical Journal. 2000;533:481.
10. Krall J, Chen J, Duffin RT, et al. Erupting Solar Magnetic Flux Ropes: Theory and Observation. Astrophysical Journal. 2001;562:1045.
11. Aoki SI, Yashiro S, Shibata K. 28th International Cosmic Ray Conference. India: Universal Academy Press; 2003. p. 2729‒2732.
12. Reinard AA. Spatial Relationship between Solar Flares and Coronal Mass. The Astrophysical Journal.  2003;682:1289.
13. Lepri ST, Zurbuchen TH. Direct Observational Evidence Of Filament Material Within Interplanetary Coronal Mass. Ejections the Astrophysical Journal Letters. 2010;723: L22.
14. Carrington RC. Description of a Singular Appearance seen in the Sun. MNRAS. 1859;20:13‒15.
15. Hodgson R. On a curious Appearance seen in the Sun. MNRAS. 1859;20:15‒16.
16. Kane RP. The idea of Space Weather–A historical perspective. Advances in Space Research. 2006;37:1261–1264.
17. Echer E, Rigozo NR, Souza MP, et al. Prediction of solar activity on the basis of spectral characteristics of sunspot number. Annales Geophysicae. 2004;22:2239–2243.
18. Noyes RW. The Sun, Our Star. USA: Harvard University Press; 1982.
19. Tandberg–Hanssen E, Emslie AG. The Physics of Solar Flares. UK: Cambridge Univiversity Press.1988;286.
20. Noble PL. Wheatland MS. The Astrophysical Journal. 2011;732–735.
21. Eddy JA. The maunder minimum. Science. 1976;192(4245):1189–1202.
22. White OR. The solar output and its variation. USA: Colorado Associated University Press; 1977.
23. Hoyt DV, Schatten KH.  The role of the Sun in climate change. USA: Oxford University Press; 1979.
24. Hoyt DV, Schatten KH. Solar Physics. 1998a;179:189.
25. Hoyt DV,  Schatten KH. Group Sunspot Numbers: A New Solar Activity Reconstruction. Solar Physics. 1998b;179(1):189–219.
26. Spiegel EA. In Lectures on Solar and Planetary Dynamos. In: Proctor MRE, Gilbert AD, editors. UK: Cambridge University Press, 1994; 245.
27. Denkmayr K, Cugnon P. Proceedings of the 5th Solar–Terrestrial Predictions Workshop. In R. Heckman, editor. Japan: Communications Research Laboratory; 1997. p. 103.
28. Hanslmeier A, Denkmayr K, Weiss P. Longterm Prediction of Solar Activity Using the Combined Method. Solar Physics. 1999;184(1):213–218.
29. Wang YM, Ye PZ, Wang S, et al. A statistical study on the geoeffectiveness of Earth–directed coronal mass ejections from March 1997 to December 2000JGR. Journal of Geophysical Research. 2002;107:1340.
30. Zhan LS, Zhao HJ, Liang HF. Prediction of sunspot numbers in the declining phase of solar cycle 23. New Astronomy. 2003;8:449–456.
31. Zhou SR, Huang G, Han ZZ, et al. The fuzzy forecast of the activity of solar active regions. Astrophysics and Space Science. 2002;280(4):369–380.
32. Xu T, Wu J, Wu Z, et al. Long–Term Sunspot Number Prediction based on EMD Analysis and AR Model. Chinese Journal of Astronomy and Astrophysics. 2008;8(3)337–342.
33. Layden AC, Fox PA, Howard JM, et al. Dynamo–based scheme for forecasting the magnitude of solar activity cycles. Solar Physics. 1991;132(1):1–40.
34. Conway AJ. Time series, neural networks and the future of the Sun. New Astronomy Reviews. 1998;42(5):343–394.
35. Brueckner GE, Howard RA, Koomen MJ, et al. The Large Angle Spectroscopic Coronagraph (LASCO). Solar Physics. 1995;162(1–2):357–402.
36. Gopalswamy N, Lara A, Lepping RP, et al. Interplanetary acceleration of coronal mass ejections. Geophysical Research Letters. 2000;27(2)145–148.
37. Gopalswamy N, Lara A, Yashiro S, et al. Coronal mass ejection activity during solar cycle 23. Netherlands: ESA Publications Division; 2003. p. 403–414.
38. Ma S, Attrill GDR, Golub L, et al. Statistical study of coronal mass ejections with and without distinct low coronal signatures. The Astrophysical Journal. 2010;722(1):289–301.
39. Proctor MRE, Gilbert AD. Lectures on Solar and Planetary Dynamos. UK: University of Cambridge; 1994.
40. Ramesh KB. Coronal mass ejections and sunspots—solar cycle perspective. The Astrophysical Journal Letters. 2010;712(1):L77–L80.
41. Low BC. Coronal mass ejections, magnetic flux ropes, and solar magnetism. Journal of Geophysical Research. 2001;106(A11):25141–25163.
42. Pontieri A, Lepreti F, Sorriso–Valvo L, et al. A Simple Model for the Solar Cycle. Solar Physics. 2003;213(1):195–201.
43. Brajša R, Whöl H, Hanslmeier A, et al. On solar cycle predictions and reconstructions. Astronomy & Astrophysics. 2009;496(3):855–861.
44. Hanslmeier A. The Sun and the Space Weather. 2nd ed. Germany: Springer; 2007.
45. Spiegel EA. Lectures on Solar and Planetary Dynamos. In: Proctor MRE, Gilbert AD, editors. UK: Cambridge University Press; 1994.
46. Letellier C, Aguirre LA, Maquet J, et al. The Astrophysical Journal. 2006;449:379.
47. Hanslmeier A, Brajša R. The chaotic solar cycleI. Analysis of cosmogenic${}^{14}C$ –data. Astronomy & Astrophysics. 2010; 509(A5):1–7.
48. Aguirre LA, Letellier C, Maquet J. Forecasting the Time Series of Sunspot Numbers. Solar Physics. 2008;249(1):103–120.
49. Orfila A, Ballester JL, Oliver R, et al. Forecasting the solar cycle with genetic algorithms. Astronomy & Astrophysics. 2002;386(1):313–318.
50. Ramesh KB, Rohini VS. 1–8Å Coronal Background X–Ray Emission and the Associated Indicators of Photospheric Magnetic Activity. The Astrophysical Journal Letters. 2008;686(1):L41–L44.
51. Gopalswamy N. Climate and Weather of the Sun–Earth System (CAWSES): Selected Papers from the 2007.
52. Gosling JT, Hildner E, MacQueen RM, et al. The speeds of coronal mass ejection events. Solar Physics. 1976;48(2):389–397.
53. Sheeley NR, Walters JH, Wang Y, et al. Continuous tracking of coronal outflows: Two kinds of coronal mass ejections. Journal of Geophysical Research. 1999;104(A11):24739–24767.
54. Gopalswamy N, et al. Magnetic Coupling between the Interior and Atmosphere of the Sun. In: Hasan SS, Rutten RJ, editor. Germany: Springer–Verlag: 2009. p. 1–557.
55. Yashiro S, Gopalswamy N, Michalek G, et al. A catalog of white light coronal mass ejections observed by the SOHO spacecraft. Journal of Geophysical Research. 2004;109(A07):105–116.
56. Kilcik A, Yurchyshyn VV, Donmez B, et al. Distribution of CME Speeds and the Temporal Variation of the Number of CMEs during the Last Two Solar Cycles: Their Possible Connection with Ap and Dst Indices. Central European Astrophysical Bulletin. 2016;40(1):111–121.
57. Andrews MD, Howard RA. A two–Type Classification of Lasco Coronal Mass Ejection. Space Science Reviews. 2001;95(1–2):147–163.
58. Cane HV, Richardson IG. Interplanetary coronal mass ejections in the near‐Earth solar wind during 1996–2002. Journal of Geophysical Research. 2003;108(A4).
59. TsudaT, Fujii R, Shibata K, et al. Kyoto Symposium. Japan: TERRAPUB.
60. Gopalswamy N, Yashiro S, Kaiser ML, et al. Characteristics of coronal mass ejections associated with long‐wavelength type II radio bursts. Journal of Geophysical Research. 2001;106(A12).
61. Harrison RA. The nature of solar flares associated with coronal mass ejection. Astronomy and Astrophysics. 1995;304:585.
62. Hundhausen AJ. Coronal Mass Ejections: Geophysical Monograph. In: Crooker N, Joselyn JA, Feynman J, editors. USA: AGU; 1997. p. 99.
63. Kim RS, Cho KS, Moon YJ, et al. Forecast evaluation of the coronal mass ejection (CME) geoeffectiveness using halo CMEs from 1997 to 2003. Journal of Geophysical Research. 2005;110(A11).
64. Lepri ST, Zurbuchen TH. Direct observational evidence of filament material within interplanetary coronal mass ejections. The Astrophysical Journal Letters. 2010;723(1):L22–L27.
65. Liu YD, Hu H, Wang C, et al. On Sun–to–Earth Propagation of Coronal Mass Ejections: II. Slow Events and Comparison with Others. Astrophysical Journal Supplementary Services. 2016;222.
66. Cyr OC, Howard RA, Sheeley NR, et al. Properties of coronal mass ejections: SOHO LASCO observations from January 1996 to June 1998. Journal of Geophysical Research. 2000;105(A8):18169–18185.
67. Webb DF, Cliver EW, Crooker NU, et al. Relationship of halo coronal mass ejections, magnetic clouds, and magnetic storms. Journal of Geophysical Research. 2000;105(A4):7491–7508.