We have considered here that the conformational properties of a DNA molecule can be mapped onto a Heisenberg spin system when spins are located on the axis forming an antiferromagnatic chain. This helps us to study the topological and elastic properties of a DNA molecule in terms of SU(2) gauge fields. The entanglement entropy of the spin system in a supercoil has been determined and it is pointed out that this effectively corresponds to the thermodynamic entropy. The model reproduces salient features of the Rod-Like-Chain model avoiding the “RLC model crisis”.

Keywords: spin system, gauge field, entanglement entropy

It is now well known that DNA can be regarded as a physical elastic object in a viscous environment. Two strands of double helix are anti-parallel and two polynucleotide chains are coiled about the same axis such that B-DNA (Z-DNA) has right-handed (left-handed) helical sense. In earlier studies it has been shown that elongation verses force characteristics of a DNA molecule¹ can be described² by the worm-like-chain (WLC) which essentially depicts a chain by an elastic continuous curve at thermal equilibrium with a single elastic constant, the persistence length A characterizing the bending energy.³ It has been shown that the analytic solution of WLC can be achieved through the mapping to a quantum mechanical problem. In fact its partition function corresponds to Euclidean path integral for a quantum dumbbell when rotations and vibrations are ignored so that it represents a rigid rotator. The generalization of the WLC with twist rigidity was considered by Bouchiat et al.⁴ and it was shown that a DNA molecule at small super coiling can be described by a thin elastic rod involving the twist rigidity. It is called the rod –like –chain (RLC) model. The partition function can be mapped onto the path integral representation for a quantum charged particle in the field of a magnetic monopole with nonquantized charge.⁴ The theory is singular in the continuum limit and needs to be regularized at an intermediate length scale. It is found that the model is in good agreement with the experimental data at small super coiling region.

In this note we shall study the specific properties of DNA by taking into consideration that the conformational properties of a DNA molecule can be mapped onto a Heisenberg spin system. In fact as two polynucleotide chains are coiled about the same axis with a specific helical sense in a DNA molecule, we may visualize it such that a spin with a specific orientation is inserted on the axis Indeed as the rotation of the two strands about the axis in the positive direction through an angle $\pi$ is identical with that of rotation about the axis in the negative direction through an angle $\pi$, we can uplift the rotation group SO(3) to SU(2). A spin is represented as a SU(2) gauge bundle.⁵ In view of this we can consider that twisting of the two strands can be taken to be represented by a spin inserted on the axis such that two adjacent coils have opposite orientations of the spin. This essentially implies that two strands twisting about the axis in the opposite direction can be designated by two spins having orientations and . When these spins are inserted on the axis such that two spins having opposite orientations are located in the two adjacent coils with lattice spacing of one period of helix this represents an antiferromagnetic spin chain. The nearest neighbor spin –spin interaction can be viewed as to represent the twisting energy.

In an earlier paper⁶ we have studied the denaturation of DNA by mapping its conformational properties onto a Heisenberg spin chain. It has been shown that denaturation occurs when the entanglement entropy of the spin chain vanishes and appears to be caused by quantum phase transition induced by a quench⁷ when the temperature effect is incorporated in the quench time. Here torsion takes the role of the external field. In a recent paper⁸ it has been pointed out that the sequence heterogeneity interplays with the entropy effects and we have the onset of denaturation bubbles. The melting profiles for different sequence-specific DNA molecules have been studied and the results are found to be in excellent agreement with experiments. We shall study here the topological and elastic properties of DNA by mapping it onto Heisenberg spin chain by utilising the fact that a spin can be treated as a SU(2) gauge bundle so that a gauge theoretic treatment of DNA can be formulated. We have shown in some earlier papers^5,9 that a spin can be represented by an SU(2) gauge bundle and we can study a spin system in terms of these gauge fields. Here we shall show that when the conformational properties of DNA are mapped onto a Heisenberg spin chain we can represent the topological properties such as the linking number in terms of these gauge fields. The bending as well as the twisting energy can be formulated in terms of the Lagrangian involving these gauge fields. It is pointed out that the thermodynamic entropy of a DNA supercoil can be represented by the entanglement entropy of the spin chain. We have analytically estimated the free energy per unit length of a DNA supercoil which corresponds to that of a strongly confined polymer in a tube and the result is found to be in good agreement with that obtained from computer simulation. It is shown that the antiferromagnetic spin chain manifests certain salient features of the rod-like-chain (RLC) model when the partition function is mapped onto the path integral representation of a quantum charged particle in the field of a magnetic monopole with nonquantized monopole charge. It is argued that this formulation helps us to avoid the “RLC model crisis” which involves the violation of rotational invariance due to the nonquantized value of angular momentum.

In sec 2 we depict DNA as a spin chain. In sec 3 and 4 we study the topological and elastic properties of a DNA molecule from an analysis of the spin system. In sec.5 we consider the entropy of a DNA supercoil. In sec.6 we compare the present formalism with the RLC model.

We consider that two polynucleotide chains are coiled about the same axis with a specific helical sense in a DNA molecule. This can be viewed as if a spin with a specific orientation is inserted on the axis of the coil such that two adjacent coils have opposite orientations of the spin. In fact with each turn two strands move in the opposite side of the axis and so the spin orientation assigned for the two adjacent coils should be opposite to each other. It may be noted that twisting of the two strands in mutually opposite directions can be taken to imply that two strands can be designated by two spins having orientations $+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and $-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. When these two spins having opposite orientations are inserted on the axis such that these are located in the two adjacent sites with lattice spacing of one period of helix this represents an antiferromagnetic spin chain. The nearest neighbor spin –spin interaction can be viewed as to represent the twisting energy (Figure 1).

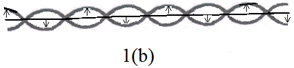
Figure 1 DNA molecule as a spin chain. (a) DNA molecule and (b) the corresponding.

As the two strands can be taken to be designated by two opposite spin orientations we can consider that a unit vector depicting the tangent $\overrightarrow{t}={\partial }_s\overrightarrow{r}$ where $\overrightarrow{r}\left(s\right)$ is a space curve parametrized by the arc length s of the helixcan be mapped onto the spin vector when the spin is located at the spatial point x on the molecular axis about which the two strands move. It is noted that any arbitrary deformation of the interwound helices such as bending, twisting and stretching will deviate the axis from a simple straight line. A spin vector in the Lie algebra of SU(2) representation can be constructed with bosonic or fermionic oscillators. We write the spin vector $\overrightarrow{S}(x)$  as

$\overrightarrow{S}(x)={\psi }_{\alpha }^{\text{†}}\left(x\right){\overrightarrow{\sigma }}_{\alpha \beta }{\psi }_{\beta }\left(x\right)$             (1)

where ${\psi }^{\text{†}}\left(\psi \right)$ is the fermionic oscillator function and ${\overrightarrow{\sigma }}_{\alpha \beta }$  is the vector of Pauli matrices. A unit vector $\overrightarrow{n}$ is constructed as  

$\overrightarrow{n}=\left({\psi }_1^{*}{\psi }_2^{*}\right)\overrightarrow{\sigma }\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\end{array}\right)$             (2)

with ${\psi }_1=\left(\cos \raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)e^{\raisebox{1ex}{$i\varphi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$

${\psi }_2=\left(\sin \raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)e^{\raisebox{1ex}{$-i\varphi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$        (3)

This helps us to write the spin vector (1) in terms of the unit vector (2) as

$\overrightarrow{S}(x)=\left(\sqrt{3}/2\right){\psi }_{\alpha }^{\text{†}}\left(x\right){\overrightarrow{\sigma }}_{\alpha \beta }^{}{\psi }_{\beta }$            (4)

We can construct a unit vector $n_{\mu }$  with $\mu =0,1,2,3$ in $3+1$ dimensions incorporating the unit vector $\overrightarrow{n}$ given by eqn. (2)

$n_{\mu }=\left(1/\sqrt{2}\right)\left({\psi }_1^{*}{\psi }_2^{*}\right){\sigma }_{\mu }\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\end{array}\right)$              (5)

with ${\sigma }_0=\text{I}$, I being the identity matrix and $\overrightarrow{\sigma }$ is the vector of Pauli matrices. We construct the topological current

$J_{\mu }=\left(1/12{\pi }^2\right){\epsilon }_{\mu \nu \lambda \sigma }{\epsilon }_{abcd}{n}_a{\partial }_{\nu }{n}_b{\partial }_{\lambda }{n}_c{\partial }_{\sigma }{n}_d$               (6)

where (a, b, c, d) correspond to (0, 1, 2, 3) and $\left(\mu ,\nu ,\lambda ,\sigma \right)$ correspond to space-time indices. The current $\overrightarrow{J_{\mu }}$ can be written in the form¹⁰

$J_{\mu }=\left(1/24{\pi }^2\right){\epsilon }_{\mu \nu \lambda \sigma }Tr(g^{-1}{\partial }_{\nu }g)(g^{-1}{\partial }_{\lambda }g)(g^{-1}{\partial }_{\sigma }g)$         (7)

with $g=n_0\text{I }+i\text{.}\overrightarrow{\sigma }$ which belongs to the group SU(2). If we demand that in Euclidean 4- dimensional space-time the field strength $F_{\mu \nu }$ of a gauge potential $A_{\mu }$ vanishes at all points on the boundary $S^3$ of a certain volume $V^4$ inside which $F_{\mu \nu }\ne 0$ the gauge potential tends to a pure gauge towards the boundary and we write

$A_{\mu }=g^{-1}{\partial }_{\mu }g$           (8)

with $g\in SU\left(2\right)$ .

We can now write the topological current given by (7) as⁵

$J_{\mu }=\left(1/16{\pi }^2\right){\epsilon }^{\mu \nu \lambda \sigma }Tr\left\{A_{\nu }{F}_{\lambda \sigma }+\left(2/3\right)A_{\nu }{A}_{\lambda }{A}_{\sigma }\right\}$         (9)

with $A_{\mu }$ given by eqn.(8) .It is noted that as the spin vector is constructed from the unit vector $\overrightarrow{n}$ given by (2) which is incorporated in the current $J_{\mu }$ as is evident from eqn. (6), we can associate spin with this current $J_{\mu }.$  

In fact we can consider the topological Lagrangian in terms of the SU(2) gauge fields in affine space

$L=-\left(1/4\right)Tr{\epsilon }^{{}_{\mu \nu \alpha \beta }}{F}_{\mu \nu }{F}_{\alpha \beta }$       (10)

This gives rise to the topological current¹¹

$\overrightarrow{J_{\mu }}={\epsilon }^{\mu \nu \lambda \sigma }{\overrightarrow{a}}_{\nu }\times {\overrightarrow{f}}_{\lambda \sigma }={\epsilon }^{\mu \nu \lambda \sigma }{\partial }_{\nu }{\overrightarrow{f}}_{\lambda \sigma }$          (11)

where we have taken the SU(2) gauge field $A_{\mu }$ and the corresponding field strength $F_{\mu \nu }$ as

$A_{\mu }=\overrightarrow{a_{\mu }}.\overrightarrow{\sigma }$ and $F_{\mu \nu }=\overrightarrow{f_{\mu \nu }}.\overrightarrow{\sigma }$             (12)

$\overrightarrow{\sigma }$ being vector of Pauli matrices. From this it appears that the spin vector $\overrightarrow{S}\left(x\right)$ can be depicted as the topological current $\overrightarrow{J_{\mu }}$ given by eqn. (11). In terms of this current a spin system on a lattice can be viewed as if currents are located on the vertices when gauge fields lie on links.⁹

In length scales of a large number of base pairs DNA in vivo is organized into topologically independent loops. The two strands of a circular DNA molecule possess as a topological invariant the number of times they wind around each other which is known as the linking number. A B-DNA molecule has one right-handed twist per $h=3.4$ nm along its length. When these are closed in a planar circle without twisting of the ends the resulting linking number is $L{k}_o=L/h={\omega }_{0}L/\left(2\pi \right)$ where $L$ is the length and ${\omega }_0$ is the spatial rotation rate of the base pairs about the central axis.¹² Deviations in the twisting rate from ${\omega }_0$ is measured relative to $L{k}_o$ through the parameter defining the excess linking $\sigma =\left(\Delta Lk/L{k}_0\right)$ where $\Delta Lk=Lk-L{k}_0$ .The linking number $Lk$ is expressed as $Lk=Tw+Wr$ where $Tw$ represents the twist corresponding to the rotation of the internal degrees of freedom about the molecule axis and $Wr$ represents the writhe.¹³⁻¹⁵ The twist measures the winding of one curve about the other. It can be mathematically expressed as¹²

$Tw={\displaystyle \underset{0}{\overset{L}{\int }}\left(ds/2\pi \right)}\left[{\omega }_0+\Omega \left(s\right)\right]=L{k}_o+\Delta Tw$           (13)

where $\Omega$ is the twist strain measuring the excess or deficit rotation of the base pairs about the axis and S defines the arc length. The writhe characterizes the chiral deformation of a curve. One can assign an orientation to a curve and compute the sum of signed crossings in a planar projection along every direction. $Wr$ is equal to the average of such sums over all projections.¹⁶

We can understand twist and writhe more explicitly from the following considerations.¹⁷ Let us take that there are two oriented non-intersecting closed curves ${\gamma }_1$ and ${\gamma }_2$ and imagine that ${\gamma }_2$ carries a unit current in the direction of its orientation. Evidently this gives rise to a magnetic field. Now applying Ampere’s law to deduce the number of times ${\gamma }_1$ encircles ${\gamma }_2$ and then using the Biot-Savert law which helps us to estimate the magnetic field due to the current we can write

$\begin{array}{l}Lk({\gamma }_1,{\gamma }_2)={\displaystyle {\oint }_{r_1}\overrightarrow{B}({\overrightarrow{r}}_1)}d{\overrightarrow{r}}_1\\ =\frac{1}{4\pi }{\displaystyle {\oint }_{{\gamma }_1}{\displaystyle {\oint }_{{\gamma }_2}{\{({\overrightarrow{r}}_1-{\overrightarrow{r}}_2)(d{\overrightarrow{r}}_1\times d{\overrightarrow{r}}_2)\}/\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|}^3}}\end{array}$          (14)

This is called the Gauss linking number which is symmetric under the interchange of ${\gamma }_1\leftrightarrow {\gamma }_2$. For a closed loop of DNA we identify the curves with the strands. Two such parallel curves $({\gamma }_1,{\gamma }_2)$ form the edges of a ribbon of width $\epsilon$. We now consider the curve $\overrightarrow{r}\left(t\right)$ running along the axis of the ribbon midway between ${\gamma }_1$and ${\gamma }_2$ and denote it as $\gamma$ . The unit tangent to $\gamma$ at the point $\overrightarrow{r}(t)$  is given by

$\overrightarrow{t}(t)=\stackrel{\cdot }{\dot{\overrightarrow{r}}}(t)/\left|\overrightarrow{r}(t)\right|$        (15)

the dot denoting the differentiation with respect to t. A unit vector $\overrightarrow{t}\left(t\right)$ perpendicular to $\overrightarrow{t}\left(t\right)$ lies in the ribbon pointing from ${\overrightarrow{r}}_1\left(t\right)$ to ${\overrightarrow{r}}_2\left(t\right)$.We can now write

$\begin{array}{l}{\overrightarrow{r}}_1(t)=\overrightarrow{r}(t)-(1/2)\epsilon \overrightarrow{u}(t)\\ {\overrightarrow{r}}_2(t)=\overrightarrow{r}(t)+(1/2)\epsilon \overrightarrow{u}(t)\end{array}$                (16)

Expressing $\dot{\overrightarrow{u}}=\overrightarrow{\omega }\times \overrightarrow{u}$       (17)

where $\overrightarrow{\omega }\left(t\right)$ is the angular velocity vector we can define twist as

$Tw=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2\pi $}\right.{\displaystyle {\oint }_{\gamma }(\overrightarrow{\omega }.\overrightarrow{t})dt}$               (18)

If we let ${\overrightarrow{r}}_1(t)$ and ${\overrightarrow{r}}_2\left(t\right)$ equal to the single axis curve $\overrightarrow{r}\left(t\right)$ in the integrand of (14) the self -linking integral known as the writhe is given by

$Wr=\frac{1}{4\pi }{\displaystyle {\oint }_{\gamma }{\displaystyle {\oint }_{\gamma }{\{(\overrightarrow{r}(t_1)-\overrightarrow{r}(t_2))((\dot{\overrightarrow{r}}(t_1)\times \dot{\overrightarrow{r}}(t_2))\}d{t}_{1}d{t}_2/\left|(\overrightarrow{r}(t_1)-\overrightarrow{r}(t_2)\right|}^3}}$                  (19)

The writhe is a property of the overall shape of the curve $\gamma$  and is independent of the ribbon that contains it .We have the relation

$Lk=Tw+Wr$               (20)

which is known as the Calugareanu-White-Fuller relation. It may be mentioned here that the expressions (19) and (20) were also derived by Frank-Kamenetskii et al.¹⁸ in the context of their study on the physical properties of circular DNAs. Indeed these authors have presented the mathematical basis of the theory of knots and links as well as the theory of ribbons in their analysis on the topological aspects of polymers and their biophysical applications. From the point of view that a DNA molecule can be depicted as a spin system we can determine the linking number from the spin degrees of freedom. It is noted that the expression of the current $J_{\mu }$ associated with the spin given by eqn.(9) essentially corresponds to the Chern-Simons secondary characteristics class . The topological charge

$q=\int J_0{d}^{3}x$         (21)

corresponds to the winding number associated with the homotopy ${\pi }_3\left(S^3\right)=Z$ and can be written as

$q=2\mu =\left(1/24{\pi }^2\right){\displaystyle \underset{S^3}{\int }{\epsilon }^{\mu \nu \lambda \sigma }Tr(g^{-1}{\partial }_{\nu }g)(g^{-1}{\partial }_{\lambda }g)(g^{-1}{\partial }_{\sigma }g)}$           (22)

This charge q essentially represents the Pontryagin index which is an integer and the relation $q=2\mu$ implies that $\mu$ corresponds to the magnetic monopole strength. This Pontryagin index can be written as the integral in the 4-dimensional manifold $M_4$ as

$q=(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$16{\pi }^2$}\right.){\displaystyle \underset{M_4}{\int }Tr(F\wedge F)}$               (23)

where F is the two-form related to the field strength associated with the $SU\left(2\right)$ gauge field $A_{\mu }$. Now from the relation

${\displaystyle \underset{M_4}{\int }Tr(F\wedge F)}={\displaystyle \underset{M_3}{\int }Tr(A\wedge dA}+\left(2/3\right)A\wedge A\wedge A)$             (24)

where $M_3$ is a three dimensional manifold and $A$ is the one-form corresponding to the $SU\left(2\right)$ gauge field $A_{\mu }$ we note that the R.H.S of eqn.(24) represents the Chern-Simons invariant and is thus found to be associated with the Pontryagin index in a 4-dimentional manifold. Noting that the Pontryagin index corresponding to the charge related to the gauge current $J_{\mu }$ given by eqn.(9) which is associated with the spin , we can consider spin in the framework of Chern-Simons topology .In fact from eqn.(11) we note that any component of the spin vector can be written as

$J_{\mu }^a(a=1,2,3)={\epsilon }^{\mu \nu \lambda \sigma }{a}_{\nu }{\partial }_{\lambda }{a}_{\sigma }$        (25)

where $a_{\nu }$ corresponds to an Abelian gauge field . When we project it onto a three dimensional manifold this corresponds to the Chern-Simons term ${\epsilon }^{\nu \lambda \sigma }{a}_{\nu }{\partial }_{\lambda }{a}_{\sigma }$ . In the Abelian theory we consider the one-form $a$  associated $S=\left(k/8\pi \right){\displaystyle \underset{M_3}{\int }{\epsilon }^{ijk}}{a}_i{\partial }_j{a}_k$          (26)

where $k$ is an integer. We now pick up some circles $C_a$ and some integers $n_a$ corresponding to representations of the Abelian gauge group. It is assumed that two curve $C_a$ and $C_l$ do not intersect for $a\ne b$. As shown by Polyakov¹⁹ the expectation value of the product

$W=\prod _a\exp (i{n}_a\underset{C_a}{\int }a$        (27)

with respect to the measure determined by $e^{iS}$ is given by

$〈W〉=\exp \left(\left(i/2k\right){\displaystyle \sum _{a,b}{n}_a{n}_b{\displaystyle \underset{C_a}{\int }d{x}^i{\displaystyle \underset{C_b}{\int }d{y}^j}}{\epsilon }_{ijk}\left\{{(x-y)}^k/{\left|x-y\right|}^3\right\}}\right)$           (28)

For $a\ne b$ this integral is essentially the linking number

$\varphi \left(C_a,C_b\right)=\frac{1}{4\pi }{\displaystyle \underset{C_a}{\int }d{x}^i{\displaystyle \underset{C_b}{\int }d{y}^j}}{\epsilon }_{ijk}\left\{{(x-y)}^k/{\left|x-y\right|}^3\right\}$       (29)

As long as $C_a$ and $C_b$ do not intersect $\varphi \left(C_a,C_b\right)$ is a well defined integer. Thus ignoring the term $a=b$, we have

$〈W〉=\exp \left(\left(2\pi i/k\right){\displaystyle \sum _{a,b}{n}_a{n}_b\varphi \left(C_a,C_b\right)}\right)$                     (30)

The appearance of linking number from the current representing the spin suggests that the linking number can be associated with a spin system.

From this analysis it appears that when a DNA molecule is represented as a spin system the linking number can be considered as a topological invariant. It should be mentioned that though the linking number is a topological invariant when it is split into twist $\left(Tw\right)$ and writhe $\left(Wr\right)$these entities are not topological invariants. Since the linking number of a closed DNA molecule remains constant during any deformation of the molecule that preserves chemical bonding, it can only be changed by mechanisms in which chemical bonds are disrupted.¹⁶

Here we study the elastic properties of a DNA molecule from an analysis of the spin degrees of freedom. As spins are considered here as gauge currents constructed from $SU\left(2\right)$  gauge fields we map the elastic properties onto the space of gauge potentials. In fact the tangent vector $\overrightarrow{t}={\partial }_s\overrightarrow{r}\left(s\right)$  where $\overrightarrow{r}\left(s\right)$  denotes a space curve parametrized by arc length $s$ of the helix can be mapped onto the spin vector represented by the vector of topological gauge current (11). Now considering that these gauge currents act as the source of $SU\left(2\right)$ gauge fields we can relate the tangent vector $\overrightarrow{t}$ to the vector of gauge potentials ${\overrightarrow{a}}_{\mu }$ where the components correspond to the $SU\left(2\right)$ gauge fields. Evidently ${\partial }_s^2\overrightarrow{r}$ corresponds to the vector of $SU\left(2\right)$ gauge field strength ${\overrightarrow{f}}_{\mu \nu }$. Using the relation (12) the internal energy corresponding to the curvature (bending) given by $\int ds{\left({\partial }_s^2\overrightarrow{r}\right)}^2$ can be written as $\int d^{3}xTr{F}_{\mu \nu }{F}_{\mu \nu }$. The twisting elastic energy can be associated with the spin-spin interaction and can be written in the continuum limit as $m^2\int {\overrightarrow{J}}_{\mu }{\overrightarrow{J}}_{\lambda }{d}^{3}x$ where ${\overrightarrow{J}}_{\mu }$ is the gauge current given by eqn. (11) and $m$ is a constant having the dimension of mass. It should be mentioned that this term corresponding to the spin-spin interaction in the continuum limit effectively represents torsion.²⁰

The elastic energy of B-DNA of length L is given by.¹²

$E_{cl}/k_{B}T=\frac{1}{2}{\displaystyle \underset{0}{\overset{L}{\int }}ds\left[A{({\partial }_s^2\overrightarrow{r})}^2+C{\Omega }^2\right]}$        (31)

where the deviation in the twisting rate from ${\omega }_0$ is described by the scalar field $\Omega \left(s\right)$,$A\left(C\right)$ being the bending (twisting) elastic constant. When we map this on the configuration space of gauge potentials associated with the spin system, we can write for the elastic energy in the continuum limit.

$E_{cl}/k_{B}T=\frac{1}{2}{\displaystyle \int d^{3}x}[ATr{F}_{\mu \nu }{F}_{\mu \nu }+C{m}^2{\overrightarrow{J}}_{\mu }{\overrightarrow{J}}_{\mu }]$               (32)

where ${\overrightarrow{J}}_{\mu }$ is given by eqn.(11). It is noted that the topological current ${\overrightarrow{J}}_{\mu }$ is related to the topological Lagrangian (10). In view of this we note that both bending energy and twisting energy involves the $SU\left(2\right)$ gauge field strength $F_{\mu {\nu }^{}}$. As in a non-Abelian gauge theory the field strength is not gauge invariant but gauge covariant any arbitrary deformation such as bending, twisting and stretching can be incorporated through gauge transformation. A significant result of this analysis is that curvature (bending) and torsion (twisting) associated with the deviation from ${\omega }_0$ is not separate entities. Indeed one is related to the other. This follows from the fact that the gauge field curvature $F_{\mu \nu }$ is incorporated in the construction of the current ${\overrightarrow{J}}_{\mu }$ in eqn. (11) which generates torsion. This essentially implies that bending induces a dynamical effect on torsional energy. In this context it may be added that Nelson²¹ suggested that intrinsic bending can have a huge effect in the transport of torsional stress along DNA.

It may be mentioned that twisting is measured by the spatial rotation rate of base pairs about the central axis which for an undistorted DNA is just ${\omega }_0$. However for a distorted DNA twisting elastic energy is non-zero when the double-helix twist is altered from ${\omega }_0$. In this case we have chiral symmetry breaking which is manifested through torsion. It is noted that in the present formalism torsion is generated by the topological current $J_{\mu }^a(a=1,2,3)$ which is related to the axial vector current $J_{\mu }^5=\overline{\psi }{\gamma }_{\mu }{\gamma }_5\psi$ associated with a chiral spinor. In fact each component of the vector ${\overrightarrow{J}}_{\mu }$ in eqn.(11) is related to the axial vector current through the relation²²

${\partial }_{\mu }{J}_{\mu }^2=-1/2{\partial }_{\mu }{J}_{\mu }^5,J_{\mu }^1=-1/2J_{\mu }^2,J_{\mu }^3=1/2J_{\mu }^2$              (33)

In quantum field theory the divergence of this current is non-zero which gives rise to the chiral anomaly caused by chiral symmetry breaking .In view of this we find that twisting elastic energy represented by torsion has a correspondence with the chiral anomaly in quantum field theory.

An interwound plectonemic supercoil consists of two helices of the same handedness and at the end of the cylindrical structure the two helices are connected. A solenoidal supercoil is closed by slow distortion of the coil into a toroidal structure. Thermal fluctuation swells up the supercoil radius to larger than the supercoil hard core radius. In fact it has been shown that a repulsive effective entropic potential arises opposing the elastically driven collapse at zero temperature.¹² It implies that thermodynamic entropy plays a significant role in a DNA supercoil (Figure 2).

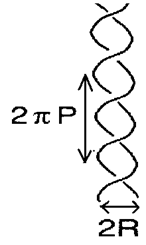
Figure 2A plectonemic superhelix, Solid line represents double helix structure of B-DNA. $R$ and $\pi P$ correspond to the radius and the pitch respectively.

When DNA molecules are treated as spin systems these attain the entanglement entropy due to the entanglement of spins. In a supercoil we can consider that the spins associated with each DNA loop are arranged along the axis of the supercoil. As we have pointed out that in a DNA molecule spins are considered to be arranged in an antiferromagnetic chain, the supercoil axis may be treated as a lattice of antiferromagnetic spin system. To have the minimal energy two adjacent spins of opposite orientations will form a singlet. Due to chirality caused by twisting strain into the loop related to torsion the spin system will be in a frustrated state as frustration leads to chirality. This frustration suggests that spin singlets are formed by resonating valence bond (RVB).²³

It has been shown in some earlier papers^24,25 that the measure of the entanglement of formation given by concurrence C for the entanglement of a pair of nearest neighbor spins is related to the Berry phase²⁶ given by $e^{i{\varphi }_B}=e^{i2\pi {\tilde{\varphi }}_B}$ which is acquired by a spin state when the spins in the system are rotated about the quantization axis (z-axis) in a closed circuit. In fact we have the relation

$C=\left|{\tilde{\varphi }}_B\right|=\left|{\varphi }_B\right|/2\pi$          (34)

It has been observed that the concurrenceassociated with the entanglement of formation for a pair of nearest neighbor spins in a frustrated system is given by $C=0.5$.²⁴ Thus the total concurrence accumulated in the spin chain is given by

$C={\displaystyle \sum _{i=1}^{\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left|{\tilde{\varphi }}_B^{}\right|=\left|{\tilde{\varphi }}_B^{}\right|\left(L/2\right)=\left(1/2\right)\left(L/2\right)=L/4}$     (35)

where L is the total number of spins in the chain and $\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ is the number of singlets. It is noted that the von Neumann entropy for an entangled spin system in a pure state is reduced to the entanglement of formation given by concurrence in a mixed state.²⁷ Thus the above expression (35) represents the entanglement entropy of the spin system. Now we consider that the supercoiled stiff polymer (DNA) is confined inside a narrow tube of radius $r$. The area of a DNA loop in a supercoil is determined by the number of coils in the loop and hence by the number of spins in the loop. When the supercoiled stiff polymer is confined in a narrow tube of radius $r$ we can associate the area of the surface of the tube with the number of spins in the DNA loop at that surface. Now from the holographic principle which states that for closed surface entropy is given by the area of the surface the entanglement entropy is found to be given by the area of the surface of the tube. Thus using eqn. (35) the entanglement entropy can be written in the form

$S_{}\approx \pi r^2/4r_0^2$              (36)

$r$ being the radius of the tube and $r_0$ a fundamental area unit. We now identify$r\approx A$, $A$ being the bending elastic constant and $r_0$ is taken to represent the radial displacement of a given point on the coil which satisfies the condition $\left|r_0\right|\le R$.²⁸ Taking the mean value $\left|r_0\right|=R/2$, the entanglement entropy is given by

$S_{}\approx \pi A^2/R^2$              (37)

Similarly for the displacement of a given point on the coil along the superciol axis which is of the order of $\pi P$,$P$ being the pitch

$S_{}\approx \pi A^2/{\left(\pi P\right)}^2$             (38)

So the total entropy is given by

$S_{}=\pi A^2/R^2+\pi A^2/{\left(\pi P\right)}^2$        (39)

Now we observe that this entanglement entropy effectively corresponds to the thermodynamic entropy. Indeed for a tube of narrow radius entanglement entropy cannot vanish whereas in the limiting case of radius $r\to 0$ we can think of zero radius (straight line) when the total elastic energy vanishes at zero temperature. In this case the entanglement entropy also vanishes. In fact at zero temperature an elastic tube will collapse into a plectonemic supercoil when subject to the constraint $\Delta Lk/L\ne 0$ .²⁹ When $\Delta Lk$ is put into writhe $\left(Wr\right)$ the twist energy becomes zero. Then we can make the plectoneme collapsed into a line which makes the bending energy zero also. Now at zero temperature the area of the loop vanishes. In this case the entanglement entropy also vanishes. In view of this we can identify the entanglement entropy as the thermodynamic entropy of the supercoil.

This helps us to compute the free energy associated with the supercoil. We note that from the relation $dF=SdT$, $F\left(T\right)$ being the free energy (temperature), the free energy per unit volume associated with the entropy given by eqn.(39) can be written as

$\Delta F/\left(K_{B}TV\right)\approx \pi A^2/\left(R^2{r}^3\right)+\pi A^2/\left\{{\left(\pi P\right)}^2{r}^3\right\}$           (40)

This gives the free energy per unit length

$\Delta F/\left(K_{B}TL\right)\approx {\pi }^{1/3}{A}^{2/3}/\left(R^{2/3}r\right)+{\pi }^{1/3}{A}^{2/3}/\left\{{\left(\pi P\right)}^{2/3}r\right\}$        (41)

Now as argued above $r$ is taken to be of the order of $A$ and hence we find

$\begin{array}{l}\Delta F/\left(K_{B}TL\right)\approx {\pi }^{1/3}{A}^{2/3}/\left(R^{2/3}A\right)+{\pi }^{1/3}{A}^{2/3}/\left\{{\left(\pi P\right)}^{2/3}A\right\}\\ {\pi }^{1/3}/\left(A^{1/3}{R}^{2/3}\right)+{\pi }^{1/3}/\left(A^{1/3}{\left(\pi P\right)}^{2/3}\right)\end{array}$         (42)

In terms of the diameter D $(D=2R)$, the confinement free energy per unit length is found to be given by

$\begin{array}{l}\Delta F/\left(K_{B}TL\right)\approx {\pi }^{1/3}{2}^{2/3}/(A^{1/3}{D}^{2/3}+A^{1/3})\\ \approx 2.32/(A^{1/3}{D}^{2/3}+A^{1/3})\end{array}$ (43)

In this context it may be mentioned that for a semiflexible polymer in a cylindrical tube of diameter D the confinement free energy per unit length has been found to be given by.³⁰

$(\raisebox{1ex}{$\Delta F$}\!\left/ \!\raisebox{-1ex}{$k_{B}TL$}\right.)=c(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$A^{1/3}{D}^{2/3}$}\right.)$         (44)

The dimensionless constant $c$ was estimated as $2.46\pm 0.07$ on computer simulation.³¹ Burkhardt²⁸ considered a continuum model of a fluctuating semiflexible polymer chain confined along an axis and concluded that $c⟩\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ which is consistent with the prediction from computer simulation. From our above analysis we note that the first term in eqn. (43) represents the free energy per unit length when the displacement of a point on the coil is in the radial direction and corresponds to that of a strongly confined polymer in a tube. We have derived the coefficient $c=2.32$ which is in very good agreement with that derived from computer simulations and also satisfies the constraint $c⟩\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. It may be mentioned that when we take the upper limit for the displacement $\left|r_0\right|=R$, we have from eqns (30) and (43) the constraint $c\ge 1.46$ which is very close to the relation $c⟩\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ derived by Burkhardt.²⁸

It is observed that the topological and elastic properties of a DNA molecule have been studied earlier by several authors using quantum mechanics. Klolodenko et al.³² studied the elastic response to elongation force for polymer chains of arbitrary stiffness using the relation between semiflexible polymers and Euclidean Dirac fermions. In case of a DNA molecule the worm-like-chain (WLC) model was introduced³ which describes a chain by an elastic continuous curve at thermal equilibrium with a single elastic constant, the persistent length A characterizing the bending energy. The WLC can be solved analytically by mapping it onto a quantum mechanical problem. Indeed the partition function is a Euclidean path integral for a quantum dumbbell. Bouchiat et al.⁴ generalized this model introducing twist rigidity $C$ and it appears that a DNA molecule can be depicted as a thin elastic rod. This rod-like-chain (RLC) model is characterized by the fact that the partition function can be mapped onto the path integral representing a charged particle in the field of a nonquantized monopole. When we describe it in terms of three Euler angles, the corresponding Hamiltonian is found to be singular and needs a small distance cut-off which is the natural length scale of the double helix pitch. The RLC model is able to reproduce the experimentally observed results relating the effects of supercoiling in the elongation force characteristics in the small supercoiling region. It also allows the specific determination of the ratio $C/{\rm A}$.

We shall consider here the analysis adopted in the RLC model and its compatibility with the Heisenberg spin chain model of DNA molecule. A given configuration of the RLC is specified in the continuum limit by the local orthonormal trihedron $\left\{{\overrightarrow{e}}_i\left(s\right)\right\}=\left\{\overrightarrow{u}\left(s\right),\overrightarrow{n}\left(s\right),\overrightarrow{t}\left(s\right)\right\}$ where $s$ is the arc length along the molecule. Here $\overrightarrow{u}\left(s\right)$ is the unit vector along the basis line and $\overrightarrow{t}\left(s\right)$ is the tangent to the chain and $\overrightarrow{n}\left(s\right)=\overrightarrow{t}\left(s\right)\Lambda \overrightarrow{u}\left(s\right)$. The evolution of the trihedron $\left\{{\overrightarrow{e}}_i\left(s\right)\right\}$ along the chain is obtained by applying the rotation $R\left(s\right)$ to a reference trihedron $\left\{{\overrightarrow{e}}_i^0\left(s\right)\right\}$ attached to a rectilinear relaxed molecule. The rotation $R\left(s\right)$ is parametrized by three Euler angles $\theta \left(s\right),\varphi \left(s\right)$ and $\psi \left(s\right)$. The reference trihedron is characterized by $\theta \left(s\right)=0$,$\varphi \left(s\right)+\psi \left(s\right)={\omega }_{0}s$ where ${\omega }_0$ is the rotation per unit length of the base axis. For given values of the Euler angles $\theta \left(s\right),\varphi \left(s\right)$ and $\psi \left(s\right)$ at the two ends $s_0=0$ and $s_1=L$ of the chain the partition function is given by $=({\theta }_1,{\varphi }_1,{\psi }_1,s_1\left|{\theta }_0,{\varphi }_0,{\psi }_0,s_0\right.)$

$=\int D({\theta }_{},{\varphi }_{},{\psi }_{})\exp \left(-\raisebox{1ex}{$E_{RLC}$}\!\left/ \!\raisebox{-1ex}{$k_{B}T$}\right.\right)$   (45)

The elastic energy $E_{RLC}$ is transformed into the integral $i\underset{t_0}{\overset{t_1}{\int }}dtL\left(t\right)$ where $L\left(t\right)$ is that of a symmetric top in a static electric field. The analytically continued partition function corresponds to the Feynman amplitude

$\begin{array}{l}⟨{\theta }_1,{\varphi }_1,{\psi }_1,s_1\left|{\theta }_0,{\varphi }_0,{\psi }_0,s_0\right.⟩\\ =\int D({\theta }_{},{\varphi }_{},{\psi }_{})\exp \left(i\underset{t_0}{\overset{t_1}{\int }}dtL\left(t\right)\right)\\ =⟨{\theta }_1,{\varphi }_1,{\psi }_1\left|\exp -i(t_1-t_0)\right.H_{top}\left|{\theta }_0,{\varphi }_0,{\psi }_0\right.⟩\end{array}$                  (46)

where $H_{top}$ is the symmetric top Hamiltonian operator acting on Euler angles wave function. However it should be observed that the analogy is a bit formal. In fact in case of symmetric top the space is that of $2\pi$ periodic functions of the Euler angles $\theta$ and$\psi$ but in the RLC model the space is that of general functions without any constraint of periodicity.

It should be noted that the elastic theory cannot be valid in the atomic scale. In fact the corresponding Hamiltonian is singular and needs a small distance cut-off which is of the order of double helix pitch. One may also argue that the RLC model ignores the helical structure of the DNA molecule.

In the depiction of DNA molecule as an antiferromagnetic spin chain we observe that the spin degree of freedom appears to be associated with three Euler angles $\theta$,$\varphi ,$and $\psi$ corresponding to an extended body . In fact it has been shown in earlier papers^33,34 that the quantization of a fermion in the framework of Nelson’s stochastic quantization procedure^35,36 can be achieved when we introduce an internal variable which appears to be a direction vector depicting the spin degrees of freedom. The direction vector effectively corresponds to a vortex line which is topologically equivalent to a magnetic flux line. When we introduce the direction vector attached to a space-time point the spherical harmonics associated with the system incorporates apart from the polar angles $\theta$ and $\varphi ,$ another angle $\psi$ which is related to the rotational orientation of the direction vector. These three angles correspond to three Euler angles associated with an extended body. Thus the spin degrees of freedom introduce three Euler angles in the system. Indeed as a spin degree of freedom appears as $SU\left(2\right)$ gauge bundle and the group $SU\left(2\right)$ is topologically equivalent to the 3-sphere $S^3$, we note that $S^3$incorporates an extended body having three Euler angle $\theta ,\varphi ,\psi$. It is observed that the spherical harmonics incorporating these three Euler angles corresponds to monopole harmonics as the eigenvalue of the operator $\raisebox{1ex}{$i\hat{\partial }$}\!\left/ \!\raisebox{-1ex}{$\partial \psi $}\right.$ corresponds to a monopole charge. Indeed we can write the corresponding harmonics as $Y_l^{m,n}$, $m\left(\mu \right)$ being the eigenvalue of the operator $\raisebox{1ex}{$i\hat{\partial }$}\!\left/ \!\raisebox{-1ex}{$\partial \varphi $}\right.\left(i\raisebox{1ex}{$\hat{\partial }$}\!\left/ \!\raisebox{-1ex}{$\partial \psi $}\right.\right)$,$l$ being the angular momentum.³⁷

This suggests that the elasticity parameters depicted in terms of these angles have a correspondence with those derived in terms of a spin chain. So we can map the elasticity parameters derived from the spin chain on those derived in the RLC model. However we note that unlike the RLC model, the helical structure of DNA is the basic ingredient of the spin chain model. Also the lattice constant which is of the order of a helix period appears to be a natural cut-off which is needed to study the elastic properties in terms of the symmetric top Hamiltonian as is envisaged in the RLC model.

It should be mentioned that the analogy of the RLC model with the quantum symmetric top is confronted with a “crisis” in the sense that the RLC analog of the angular momentum is not quantized as the physical states of an elastic rod representing a double helix are not invariant under $2\pi$ rotation about its axis .This phenomenon is known as the “RLC model crisis”. In this context we may add that the Dirac quantization condition suggests that the monopole charge $\mu$ takes the values $0,\pm 1/2,\pm 1,\pm 3/\mathrm{2........}$  However in an entangled spin system the monopole charge undergoes a renormalization group (RG) flow.^38,39

The rules for the RG flow of the monopole charge known as the $\mu$-theorem are as follows. When the monopole charge depends on a certain parameter $\lambda$ we have

1. $\mu$ is stationary at fixed points ${\lambda }^{*}$ of the RG flow
2. At the fixed points $\mu \left({\lambda }^{*}\right)$ is equal to the monopole charge given by quantized values $(\mu =0,\pm 1/2,\pm \mathrm{1......})$
3. $\mu$ decreases along the RG flow i.e. $L\left(\raisebox{1ex}{$\partial \mu $}\!\left/ \!\raisebox{-1ex}{$\partial L$}\right.\right)\le 0$ where $L$ is a scale parameter.

In view of this analysis we now note that the nonquantized angular momentum related to the violation of rotational invariance in RLC model can be associated with the RG flow of the monopole charge when it is mapped onto an antiferromagnetic spin chain. Indeed Bouchiat et al.⁴ have pointed out that the writhe partition function Fourier transform corresponds to the quantum mechanical problem of a charged particle in the field of a monopole with nonquantized charge. These authors have prescribed a local writhe formula in terms of the Euler angles $\varphi (s)$ and $\psi (s)$ defining a line integral

$\chi =\varphi (L)+\psi (L)={\displaystyle \underset{0}{\overset{L}{\int }}ds(\dot{\psi }+\dot{\varphi })}$         (47)

The total twist can be written as

$Tw=\underset{0}{\overset{L}{\int }}ds(\dot{\psi }+\dot{\varphi }\cos \theta )$        (48)

A “local writhe” $\chi W$ is defined as

$\chi W=\chi -Tw={\displaystyle \underset{0}{\overset{L}{\int }}ds\dot{\varphi }(1-\cos \theta )}$         (49)

They have shown that $\chi W$ can be written as the line integral

$\int d\varphi A_{\phi }=\int {\overrightarrow{A}}_m\left(\overrightarrow{r}\right)d\overrightarrow{r}$ where $A_{\varphi }=(1-\cos \theta )$ is identified as the $\varphi$-component of the potential vector ${\overrightarrow{A}}_m\left(\overrightarrow{r}\right)$ of a magnetic monopole of charge unity. In fact for a closed circuit we have the relation

$\underset{0}{\overset{2\pi }{\int }}{A}_{\varphi }d\varphi =2\pi (1-\cos \theta )$            (50)

It is observed that the holonomy given by eqn. (50) effectively corresponds to the Berry phase²⁶ acquired by a quantum state while traversing a closed path. In fact the Berry phase acquired by a spin state in a spin $1/2$ chain when the Hamiltonian is parallel transported along a closed circuit is given by^24,25

${\varphi }_B=\pi (1-\cos \theta )$              (51)

It is noted that the holonomy given by eqn.(50) is twice this phase factor . The effective monopole charge associated with a spin state in an entangled spin system is given by the relation

${\mu }_{eff}=\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)(1-\cos \theta )$          (52)

which follows from the relation ${\varphi }_B=2\pi \mu$.^39,40 Evidently the monopole charge takes nonquantized value apart from the situation when the polar angle $\theta$ of the spin axis with the quantization axis is given by $\theta =0,\pi /2$ and $\pi$. This nonquantized monopole charge takes values on the $RG$ flow of the monopole charge in an entangled spin system.⁴¹ Thus we observe that when we map a DNA molecule onto an antiferromagentic spin system the salient features of the RLC model are well reproduced avoiding the “RLC model crisis”.

We have shown that a DNA molecule can be treated as a quantum spin system such that spins are located on the axis forming an antiferromagnetic chain .These spins can be associated with  gauge field currents when gauge fields lie on the links. We have studied the topological properties of a DNA molecule and formulated the elastic properties such as bending (curvature) and twisting (torsion) in terms of these gauge fields. A significant result of this formalism is that bending and twisting are not independent entities. In fact bending influences the propagation of twisting strain along the DNA which has been supported by experiments.

The formulation of DNA supercoil in terms of an antiferromagnetic spin chain gives rise to the entanglement entropy which induces the entropic potential associated with the free energy per unit length corresponding to the entropy cost of confining a stiff polymer inside a narrow tube. The entanglement entropy effectively represents the thermodynamic entropy and this repulsive entropic potential opposes the elastically driven collapse of a supercoil which can occur at zero temperature.

Finally, we have observed that the spin chain model reproduces the salient feature of the RLC model when the partition function is mapped onto the path integral representation of a quantum charged particle in the field of a magnetic monopole with nonquantized charge. However in this case the RLC model crisis is avoided as the nonquantized monopole charge appears to take values on the flow of the monopole charge in an entangled spin system.

The authors are grateful to express my deep gratitude to my beloved Sir Prof. Pratul Bandyopadhyay for helpful discussion.

1. SB Smith, L Finzi, C Bustamante. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 1992;258(5085):1122−1126.
2. C Bustamante, JF Marko, ED Siggia. et al. Entropic elasticity of lambda-phage DNA. Science. 1994;265(5178):1599−1600.
3. M Fixman, J Kovac. Polymer conformational statistics. III. Modified Gaussian models of stiff chains. J Chem Phys. 1973;58:1564.
4. C Bouchiat, M Mezard. Elasticity Model of a Supercoiled DNA Molecule. Phys Rev Lett. 1997;80:1556.
5. P Bandyopadhyay. The geometric phase and the spin-statistics relation. Proc Roy Soc(Londan)A. 2010;466(2122):2917−2932.
6. SS Roy, P Bandyopadhyay. Phys Lett A. 2013;337:2884.
7. B Basu, P Bandyopadhyay, P Majumdar. Magnetic-field dependence of the entanglement entropy of one-dimensional spin systems in quantum phase transitions induced by a quench. Phys Rev A. 2012;86:022303.
8. SS Roy, P Bondyopadhyay. Entropy-driven denaturation and bubble nucleation in DNA melting. Euro Phys Lett. 2015;109(4):48002.
9. G Goswami, P Bandyopadhyay. Spin system, gauge theory and renormalization group equation. J Math Phys. 1995;34:749.
10. AI Abanov, PB Wiegmann. Theta-terms in nonlinear sigma-models. Nucl Phys B. 2000;570(3):685−698.
11. M Carmeli, S Malin. The gauge-theoretical structure of general relativity and the new conserved current. Ann Phys.1977;39(1):319−330.
12. JF Marko, ED Siggia. Statistical mechanics of supercoiled DNA. Phys Rev E. 1995;52:2912.
13. G Calugareanu. Sur les classes d’isotopie des noeuds tridimensionnels et leurs invariants. Czechoslovak Mathematical Journal. 1961;11(4):588–625.
14. JH White. Self-Linking and the Gauss Integral in Higher Dimensions. Am J Math. 1969;91(3):693.
15. FB Fuller. Decomposition of the linking number of a closed ribbon: A problem from molecular biology. Proc Natl Acad Sci. 1978;75:3557−3561.
16. D Swigon. Mathematics of DNA Structure,Function and Interactions. In: Benham CJ, Harvey S, Olson WK, et al. editors. New York: Springer Science Business Media; 2009. p. 335.
17. M Stone, P Goldbart. Mathematics for Physics. London; Pimander Casaubon.
18. Frank Kamenetskii, Vologodskii. Topological aspects of the physics of polymers: The theory and its biophysical applications. Sov Phys Usp. 1981;24:679.
19. AM Polyakov. Fermi-Bose Transmutations Induced By Gauge Fields. Mod Phys Lett A. 1988;3(3):325−328.
20. A Bandyopadhyay, P Chatterjee, P Bandyopadhyay. SL(2,C)-gauge theory,N=1 supergravity and torsion. Gen Rel Grav. 1986;18:1193−1205.
21. P Nelson. Transport of torsional stress in DNA. Proc Natl Acad Sci U S A. 1999;96(25):14342−14347.
22. A Roy, P Bandyopadhyay. Topological aspects of a fermion and the chiral anomaly. J Math Phys. 1989;30(10):2366.
23. PW Anderson. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science. 1987;235:1196−1198.
24. B Basu, P Bandyopadhyay. A geometrical approach towards entanglement. Int J Geo Meth Mod Phys. 2007;9:707−716.
25. B Basu, P Bandyopadhyay. Spin entanglement of two delocalized Fermions and Berry phase. J Phys A. 2008;41:055301.
26. MV Berry. Quantal phase factors accompanying adiabatic changes. Proc Roy Soc A. 1984;392:45.
27. TJ Osborne, MA Nielson. Entanglement in a simple quantum phase transition. Phys Rev A. 2002;66:032110.
28. TW Burkhardt. Free energy of a semiflexible polymer confined along an axis. J Phys A Math Gen. 1955;28:L629.
29. NG Hunt, JF Hearst. Elastic model of DNA supercoiling in the infinite‐length limit. J Chem Phys. 1991;95:9329.
30. T Odijk. Theory of lyotropic polymer liquid crystals. Macromolecules. 1986;19:2313.
31. M Dijkstra, D Frenkel, HNW Lekkerkerker. Confinement free energy of semiflexible polymers. Physica A.1993;193(3-4):374−393.
32. KA Kholodenko, T Vilgis. Elastic response of the Dirac chain. Phys Rev E. 1944;50:1257.
33. P Bandyopadhyay, K Hajra. Stochastic quantization of a Fermi field: Fermions as solitons. J Math Phys. 1987;28(3):711.
34. K Hajra, P Bandyopadhyay. Equivalence of stochastic and Klauder quantization and the concept of locality and nonlocality in quantum mechanics. Phys Lett A. 1991;155(1):7−14.
35. E Nelson. Derivation of the Schrödinger Equation from Newtonian Mechanics. Phys Rev. 1966;150:1079.
36. Edward Nelson. Dynamical theory of Brownian motion. New Jersey: Princeton University Press; 1967. p. 148.
37. CA Hurst. Charge quantization and nonintegrable Lie algebras. Ann Phys. 1968;50(1):51−75.
38. P Bandyopadhyay. Conformal field theory, quantum group and Berry phase. Int J Mod Phys A. 2000;15(10):1415.
39. P Bandyopadhyay. Anisotropic spin system, quantized Dirac monopole and the Berry phase. Proc Roy Soc A. 2011;467(2126):427−438.
40. S Singha Roy. DNA Molecule as a Spin System and the Symmetric Top Model. Theoretical Physics. 2017;2(3):141−144.
41. S Singha Roy, P Bandyopadhyay. Quantum perspective on the localized strand separation and cyclization of DNA double helix. Phys Lett A. 2018;382(30):1973−1977.