The article presents experimental evidence of the dependence of the values of fundamental physical constants on five fundamental interactions, as well as the polarization of the physical vacuum.

Keywords: physical vacuum, fundamental constants, polarization, fine structure constant, Newton's gravitational constant, Coulomb's constant, Planck's constant.

PACS: 01.10.Fv, 04.50.-h, 12.10.Kt, 95.36.+x, 98.80.-k

At the beginning of the 21st century, another problem appeared in physics, which had not previously been identified as one of the most important fundamental physical problems. We are talking about the problem of fundamental physical constants. It naturally grew on the basis of a large number of accumulated results of research in the field of elementary particle physics and cosmology.^1-4 Thanks to this line of research, a very large number of new fundamental physical constants have appeared, which have already been singled out in a separate class - “atomic and nuclear constants”. It should be noted that their number far exceeds the number of all other constants combined. In total, hundreds of physical constants are currently used in physics. Their list, recommended by CODATA 1998, has about 300 constants. The presence of a large number of fundamental physical constants indicates that the modern understanding of fundamentality should be clarified. If we recognize the existence of some primary “truly” fundamental constants, then the presence of a large number of fundamental constants in modern physics should be explained by their origin from basic constants. A large number of constants, despite the fact that they are all classified as fundamental, calls into question the very idea of ​​their fundamentality. The same problem of fundamentality can be seen in the family of elementary particles. A large number of particles, despite the fact that all of them were classified as elementary, cast doubt on the very idea of ​​their elementarity. In general, the problem of fundamental physical constants Kosinov N.V., deputy Director of the Institute for the Problems of Physical Vacuum, formulated as follows: “The growth in the number of constants claiming the status of fundamental ones eliminates the very idea of ​​the unity of physical phenomena and unreasonably increases the number of new entities. Hundreds of constants cannot have a fundamental status. Fundamentality can only be inherent in a very small number of physical constants.”¹

Thus, there is a big contradiction between the minimum required number of fundamental constants and their real abundance. It can be assumed that the currently known constants are composite. Then the question arises: what new irreducible constants can they consist of and how are they related to each other?.⁴ However, in the theory of physical vacuum, polarization characterizes the state of the medium, and fields are factors in changing this state. Indeed, in dielectrics and magnets, the magnitudes of polarizations are associated with the configurations of electric dipoles and magnetic moments, and the fields are associated with the forces that cause a change in these configurations. Thus, fields act as a cause, and polarizations - as a consequence of this cause. In this regard, it can be said that in these theories of the polarization substance, the polarization-field concept has been established as a set of representations of the interaction of various fields with dielectrics and magnets. Since the polarizations of the physical vacuum (dark matter) do not fundamentally differ from the polarizations of matter, we can conclude that the values ​​of the fundamental constants are determined by the fundamental interactions and the polarization medium in which the processes take place. The article below presents examples that confirm this conclusion when using the continuum methodology and its conservation laws. The methodology allows modeling gravitational, Coulomb, weak and strong interactions, as well as the interaction of baryon and dark matter (fifth force) from a unified standpoint.

The role of the physical vacuum in the Large Hadron Collider

Until recently, it was believed that the use of such an important connection as the unitarity condition (the statement that the total probability of all elastic and inelastic processes in proton collisions must be equal to unity) makes it possible to completely clarify the spatial picture in the LHC of the interaction of protons and its evolution with a change in energy. However, the results of recent experiments obtained at the LHC, where the proton collision energy reaches 13 [TeV], casts doubt on the reliability of the unitarity condition, when two channels of elastic and inelastic proton collisions are rigidly connected to each other in the probability of particle production events and completely describe the spatial picture. Recognition of the polarization of the quantum vacuum (dark matter) under the action of ultrarelativistic protons and superpowerful magnetic and electric fields leads to the creation of jets of unstable particles in the LHC and distorts the spatial picture of the proton interaction region accepted in the SM, i.e. adds a third channel.³ Today, scientists at the Large Hadron Collider at CERN think they may have discovered a new particle that decays to produce muon pairs in the narrow energy peak of colliding protons, strictly defined at 28 GeV. The new result was published as a preprint for ArXiv, and the paper by Roger Barlow was published on November 13, 2018.⁵ The LHC collaborations have very strict internal validation procedures and we can be sure that the authors got the sums right when they report a "standard deviation value of 4.2σ". If this particle really exists, then it must be outside the Standard Model. In most cases, muon pairs come from different sources from two different events, not from the decay of a single particle. If you try to calculate the original mass in such cases, it will spread over a wide range of energies rather than creating a narrow peak. In a new experiment, the CMS detector detected a large number of muon pairs and, by analyzing their energies and directions, found that these pairs were produced by the decay of a single parent particle. This may indicate the instability of the quantum vacuum (dark matter). You can look at Figure 1 and judge for yourself. Is this a real peak and not just a statistical fluctuation due to a random spread of dots in the background (dashed curve)? If this is real, then it means that some of these pairs of muons actually originated from a large dark matter parent particle that decayed to emit muons, and none of these particles have ever been observed before.⁵

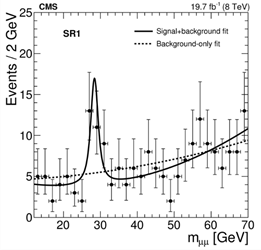
Figure 1 Peak of energy at 28GeV in the interaction of protons with a new dark matter particle (fifth interaction) in the LHC.

The CMS collaboration in experiments at the Large Hadron Collider in 2019 for the first time demonstrated a decrease in the mass of the t-quark with increasing energy.⁶ The distribution of reaction products in pp collisions with energies from 1 [TeV] to 13 [TeV] was studied. It was possible to establish that the decrease in the mass of elementary particles obtained by increasing the energy to 13 [TeV], as well as the change in the value of the interaction constants at a 95% confidence level, depend on the energy at which the measurements were made. This effect, the CMS collaboration, is explained by vacuum polarization.⁶

Changes in the fine structure constant (α) and the value of the speed of light (c) during the evolution of the universe

One of the fundamental physical constants is the fine structure of matter. The concept of fine structure (α) was introduced into physics in the 1920s by Arnold Sommerfeld to describe the experimentally discovered energy sublevels in the emission spectra of the hydrogen atom. Since then, many other manifestations of the same constant connection have been discovered in various phenomena associated with the interactions of elementary particles. In quantum electrodynamics, the fine structure constant is a measure of electromagnetism - one of the main fundamental forces in nature (the others are gravity, the weak nuclear force, and the strong nuclear force). The electromagnetic force keeps the electrons moving around the nucleus in the atom of the universe, otherwise all matter would fly apart. At present, the following value of the fine structure of elementary particles has been experimentally obtained in quantum electrodynamics:

α = 7.2973525376 (50) × 10ˉ³ = 1 / 137.035999679

$\alpha = \frac{\text{e}²}{\hslash \text{c }4{\text{πε}}_{\text{0}}}= \frac{\text{e}²}{2{\text{ε}}_{\text{0}}\text{hc }}$   (1)

Where e is the elementary electric charge,

ℏ = h / 2π is the Dirac constant (or the reduced Planck constant),

c is the speed of light in vacuum,

ε₀ is the dielectric constant.

Until recently, it was believed that this is an unchanging force in time and space. However, in an article published on April 27, 2020 in the journal Science Advances, scientists from the University of South Wales in Sydney reported that four new measurements of light emitted by a quasar 13 billion light-years from Earth confirm past research by Professor John Webb, who found variations in fine structure values. Based on the results of a new study using data from NASA's Chandra X-ray Observatory and XMM-Newton, he stated: “We found a hint that the fine structure constant number was different in certain regions of the universe. Not only depending on the age of the universe, but also in the direction of the universe, which is really strange. Not only do universal constants appear to be variable at the outer edges of the cosmic universe, anomalies also only occur in one direction. Thus, the Universe cannot be isotropic in terms of the laws of physics, that is, it is statistically different in all directions. In fact, it may contain some directions or preferred directions in which the laws of physics change. In other words, the Universe in some sense has a dipole structure”.² In the article “Investigating Cosmic Isotropy Using a New Sample of X-Ray Clusters of Galaxies Using the LX−T Scaling Relationship,” the astrophysicists write: “In this paper, we investigate the directional behavior of the X-ray luminosity-temperature (LX−T) dependence of galaxy clusters. There is a close correlation between the luminosity and temperature of the intracluster medium emitting X-rays. Although the measured luminosity depends on the underlying cosmology, the temperature can be determined without any cosmological assumptions. Using this property, one can effectively check the isotropy of cosmological parameters over the entire extragalactic sky. Here we have used 313 uniformly selected X-ray galactic clusters from the MCXC catalog and for all we have obtained temperatures cut from the core. We found that the behavior of the LX-T ratio is highly dependent on the direction of the sky. In the joint analysis of three samples, the final anisotropy is further enhanced (∼5σ) towards (l,b)∼(303º, −27º), which is in good agreement with other cosmological studies.⁷ In 2019, the European Space Agency's Gaia space telescope monitors the active stellar stream S1 moving at a speed of 310 m/s relative to the solar system. The author of the study, Pierre Sakivi, proposes to identify weaklings, candidates for the role of the main component of cold dark matter and a new interaction force (fifth force) that drives stellar streams. In 2016, Dr. Attila Krasnahorkay and his team from the Institute for Nuclear Research of the Hungarian Academy of Sciences in Debrecen, Hungary published their new discovery for the first time in the journal Physical Review Letters.⁸ Hungarian physicists say they are discovering new evidence hinting at a fifth fundamental force of nature. In the experiment, when lithium-7 was fired with protons, as a result of the collision, unstable nuclei of beryllium-8 were formed, which then decayed into pairs of electrons and positrons. Approximately, when firing at a target at a 140 degree angle, the number of these pairs increased, creating a slight bulge, before dropping again at higher angles. According to Krasnahorkay and his team, this “ejection” indicated the appearance of a new particle. They calculated that the mass of this new particle would be around 17 MeV, which is not what is expected for a "dark photon" but could indicate something completely different. The end result was a new bosonic particle that was only 34 times heavier than an electron.⁹ It can be seen from the graph (Figure 2) that deviations are observed only for two energy values ​​of incident protons Ep=1.10 MeV and Ep=1.04 MeV, and there are no other energy indicators. For protons with energies below Ep=1.04-1.10 MeV, there is no burst, indicating the decay of a new particle, Ep=0.80 MeV. However, no bulge was observed for protons with Ep=1.20 MeV either. This indicates the fact of the resonant interaction of protons with a new particle of dark matter. Andrey Rostovtsev, a Russian professor, Doctor of Physical and Mathematical Sciences, was skeptical about the discovery of Professor Attila Krasnagorkay. In the article “Hungarian physicists discovered the fifth force of nature?” in Gazeta.ru on May 26, 2016, he stated: “Deviations are observed only at two values ​​of the energy of the incident protons; this is not the case with other energy indicators. The energy of the proton changed a little - and the "splash" disappeared. This usually happens when certain experimental difficulties arise.” At the same time, Rostovtsev said: "Beryllium is also beryllium in Africa." It seemed to me that Rostovtsev's statement is not convincing enough, since he ignores the role of resonance in the formation of beryllium, and electron-positron pairs during the decay of a new dark matter particle. And the role of resonances in the occurrence of fluctuations and the birth of particles in the cosmic environment and vacuum is undeniable. I published the article "Resonance - it is also resonance in Africa" and sent it to Andrey Rostovtsev. And so, in 2019, Attila Kraznahorsky confirmed the discovery of the fifth interaction in new experiments with helium.⁹ In a new experiment conducted in 2019 by A.J. Krasznahorkay (Institute for Nuclear Research, Debrecen, Hungary) with an improved detector, the previous results obtained with ⁸Be were verified and refined, and new measurements were made with ⁴He nuclei, when a hydrogen target was bombarded with a proton beam. An additional peak corresponding to the birth of a new particle with the same mass of 17MeV as in the case of ⁸Be nuclei was observed both in the energy spectrum with a statistical significance of 7.1σ and in the angular correlations (e+e-) with a significance of 7.2σ. Further verification of the hypothesis about the production of the X17 particle can be performed in several independent experiments. Thus, now helium has come to Africa in company with beryllium. Isn't it time to admit that the quantum vacuum (dark matter), and not the target, is to blame for the resonant production of a new X17 particle at a proton energy of 17 MeV. This experiment of the Hungarian researcher Dr. Attila Kraznahorsky interested Professor John Web6a as a possible reason for the anisotropy of the fine structure value in a strictly defined direction of motion in the Universe (l, b) ∼ (303º, −27º). A group of theoretical physicists led by Jonathan Feng from the University of California (Irvine, USA) decided to check the results of their Hungarian colleagues. Professor Yonotan Feng has carefully studied the work of Dr. Attila Kraznachorsky and stated that the fifth interaction does not violate any laws of nature. The new scalar field may belong to a hypothetical dark matter particle, the protophobic X-boson, which, like the Higgs boson, creates a scalar field responsible for the fifth interaction between dark matter and ordinary (baryonic) matter. Dr. Jonathan Fehn of the University of California, Irvine, said in a 2017 press release: “For decades, we have known about the four fundamental forces: gravity, electromagnetism, and the strong and weak nuclear forces. The discovery of a possible fifth force will completely change our understanding of the Universe, which will entail the unification of the fifth force and dark matter”.¹⁰ An analysis of the experimental data related to the study of the anisotropy of physical space suggests the existence of a fifth interaction (fifth force). If the anisotropy in the value of the fine structure constant in a strictly defined direction of motion in the Universe (l, b) ∼ (303º, −27º) can be explained by vacuum polarization under the influence of the fifth interaction, then, established by Professor John Webb, the dependence of the fine structure value on the age of the Universe, possibly due to changing physical conditions in the early universe.¹¹ The interaction of the electromagnetic field with the vacuum of the electron-positron field leads to the dependence of the speed of light propagation on the radiation temperature.¹² When the vacuum is polarized and transformed into a substance, the change in the vacuum energy w can be represented as a sum :

w = wᵖ + wᵉͬ   (2)

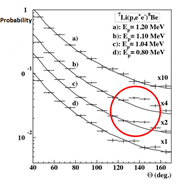
Figure 2 The probability of interaction of protons with a new dark matter particle (fifth interaction).

where wᵖ is the vacuum polarization,

wᵖ << E² / 8π;  (3)

wᵉͬ is the change in the energy of the substance at the production of particles

wᵉͬ =eETϗ,   ϗ$=\frac{{\text{e}}^2{\text{E}}^2\text{T}}{4{\text{π}}^3}\text{exp}\left(-\text{π}\frac{{\text{m}}^2}{\text{ ћ E}}\right)$   (4)

The creation of particles is the main reason for the change in the energy of the vacuum. The small value of the reverse reaction wᵖ implies the limitation on the electric field E strength for the given time T (Es ≈ 10¹⁶ [V × cmˉ¹] is the critical Schwinger’s field).¹² For an electromagnetic field, the polarization energy density of a quantum vacuum can also be represented as the sum of two terms (2). Where is the first term wᵖ (w₀) quadratic in the electric and magnetic fields:

$w_0=\frac{\left(E^2+H^2\right)}{8\pi }$   (5)

determines the energy of a non-interacting electromagnetic field before critical values electric strengths Schwinger’s field Es = 1.32 × 10¹⁶[V × cmˉ¹] and magnetic field strength H = 10¹⁶ [Gs]. The second term, wᵉͬ (w₁), describes the interaction of photons due to the production of electron-positron pairs:¹²

$w_I=2D\left[3E^2{E}^2-H^2{H}^2-\left(E^2{H}^2+H^2{E}^2\right)\right]+7D\left[{\left(EH\right)}^2+{\left(HE\right)}^2\right]$   (6)

The constant D can be calculated by the methods of quantum electrodynamics¹² and in Gaussian units

$D\equiv \eta \frac{\text{ћ }³}{\text{m}⁴{\text{c}}^{\text{5}}}$   (7)

Where η is the dimensionless coefficient

$\text{η}\equiv \frac{\text{α}²}{45\times \left(4\text{π}\right)²}\approx 7.5\times 10{ˉ}^9$   (8)

α is the fine structure constant (1),

m is the mass of the electron,

c is the speed of light.

It is convenient D to write the coefficient through the Compton wavelength of the electron $ƛ=\hslash /mc$  in the form:¹²

$D=\eta \frac{{ƛ}^3}{m{c}^2}$   (9)

It is of interest to estimate the value of the energy $w_I/w_0$  ratio. This quantity is equal to the ratio of the energy of the field contained in the volume ${ƛ}^3$ to the rest energy of the electron. In addition, this ratio must also be multiplied by a small dimensionless coefficient $\eta$ . For a magnetic field strength of the order of $H\sim {10}^{6}Gs$ , we obtain $w_I/w_0\sim {10}^{-20}$ , so the contribution of the interaction to the total field energy is indeed minimal.

Let us move on to the description of the electromagnetic field in terms of the Fourier components of fields, using the expansion of fields in plane waves,

$E\left(r,t\right)={\displaystyle \sum _k{E}_k\left(t\right)e^{ikr}},H\left(r,t\right)={\displaystyle \sum _k{H}_k\left(t\right)e^{ikr}}$   (10)

Then the total Hamiltonian of the field in the volume, following (2), is the sum of the free Hamiltonian and the interaction Hamiltonian

$H=H_0+H_I$ ,  (11)

$H_0=\frac{V}{8\pi }{\displaystyle \sum _k\left(E_k^{+}{E}_k+H_k^{+}{H}_k\right)}$ ,  (12)

$\begin{array}{c}{H}_I=2VD{\displaystyle \sum _{\left\{k_i\right\}}\{3\left(E_{k_1}^{+}{E}_{k_2}\right)\left(E_{k_3}^{+}{E}_{k_4}\right)-\left(H_{k_1}^{+}{H}_{k_2}\right)\left(H_{k_3}^{+}{H}_{k_4}\right)}-\\ -\left(E_{k_1}^{+}{E}_{k_2}\right)\left(H_{k_3}^{+}{H}_{k_4}\right)-\left(H_{k_4}^{+}{H}_{k_3}\right)\left(E_{k_2}^{+}{E}_{k_1}\right)\}\Delta \left(k_1-k_2+k_3-k_4\right)+\\ +7VD{\displaystyle \sum _{\left\{k_i\right\}}\left\{\left(E_{k_1}^{+}{H}_{k_2}\right)\left(E_{k_3}^{+}{H}_{k_4}\right)+\left(H_{k_4}^{+}{E}_{k_3}\right)\left(H_{k_2}^{+}{E}_{k_1}\right)\right\}\Delta \left(k_1-k_2+k_3-k_4\right).}\end{array}$   (13)

Here $\Delta \left(k\right)=1$ , if $k=0$ and $\Delta \left(k\right)=0$ if $k\ne 0$ . In (12) and (13), we can move on to the operators of the creation $a_{kj}^{+}$  and destruction $a_{kj}$  of photons, using the representations of the operators of the Fourier components of fields:

$\begin{array}{c}{E}_k=-i\sqrt{\frac{2\pi \hslash {\omega }_k}{V}}{\displaystyle \sum _j\left(a_{kj}^{+}-a_{-kj}\right)e_j\left(k\right)},\\ H_k=ic\sqrt{\frac{2\pi \hslash }{V{\omega }_k}}{\displaystyle \sum _j\left(a_{kj}^{+}+a_{-kj}\right)\left[k\times e_j\left(k\right)\right]},\end{array}$   (14)

Where, ${\omega }_k=ck$ , and for the polarization vectors $e_j\left(k\right)$ , the orthonormality and completeness conditions are valid:

$e_{j_1}^{\ast }\left(k\right)e_{j_2}\left(k\right)={\delta }_{j_1{j}_2},{\displaystyle \sum _j{e}_j^{\alpha \ast }\left(k\right)e_j^{{\alpha }^{\prime }}\left(k\right)={\delta }_{\alpha {\alpha }^{\prime }}}-\frac{k_{\alpha }{k}_{{\alpha }^{\prime }}}{k^2}$ ,  (15)

as well as conditions

$k{e}_j\left(k\right)=0,e_j^{\ast }\left(-k\right)=e\left(k\right)$   (16)

The free Hamiltonian of the field (12) is reduced to the sum of the Hamiltonians of harmonic oscillators,

$H_0={\displaystyle \sum _{kj}\hslash {\omega }_k\left(a_{kj}^{+}{a}_{kj}+\frac{1}{2}\right)}$   (17)

The electromagnetic field, taking into account nonlinear effects, is characterized by the complete Hamiltonian (11). To take into account the interaction in a many-particle system, as a rule, the Hamiltonian of non-interacting particles is chosen as the leading approximation, in our case it is (17), and the interaction Hamiltonian (13) is considered as a perturbation. This choice, as noted above, is not the best, since in the leading approximation the effects caused by the interaction are entirely ignored, which in the case under consideration, although small, can, as we will see, lead to qualitatively new effects. From the self-consistent approach to the description of many-particle systems it is known that taking into account interaction effects in the central approximation leads to a change in the dispersion law of the original particles and, thus, we move from the representation of free particles to the language of collective excitations - quasiparticles. It is natural to assume that in the case considered here, interaction effects will lead to a renormalization of the “primary” speed of light, included in the free Hamiltonian. Taking into account this consideration, we split the complete Hamiltonian (17) into the central part and the perturbation differently, namely

$H=H_S+H_C$ ,  (18)

Where we choose the self-consistent (or approximating) Hamiltonian in the form similar to the free Hamiltonian (17), but with the speed of light  renormalized due to the photon-photon interaction:

$H_S={\displaystyle \sum _{k,j}\hslash {\tilde{\omega }}_k{a}_{kj}^{+}{a}_{kj}+E_0}$ ,  (19)

Where ${\tilde{\omega }}_k=\tilde{c}k$

The correlation Hamiltonian describing the interaction of renormalized or “dressed” photons is chosen so that the total Hamiltonian remains unchanged:

$H_C={\displaystyle \sum _{k,j}\hslash \left({\omega }_k-{\tilde{\omega }}_k\right)a_{kj}^{+}{a}_{kj}}+{\displaystyle \sum _k\hslash {\omega }_k}-E_0+H_I$ .  (20)

This Hamiltonian describes the interaction of photons propagating at a renormalized speed of light, which we will not consider. Formulas (19), (20) include a term that does not contain operators, taking into account which is necessary for the correct formulation of the self-consistent field model. We chose it because the approximating Hamiltonian (19) is as close as possible to the exact Hamiltonian. It means that it is necessary to require that the value $I\equiv \left|\langle H-H_S\rangle \right|=\left|\langle H_C\rangle \right|$ be minimal, i.e., equal to zero. From here, we obtain the conditions natural for the theory of a self-consistent field:

$\langle H\rangle =\langle H_S\rangle ,\langle H_C\rangle =0$   (21)

Averaging is performed using the statistical operator

$\rho =\exp \beta \left(F-H_S\right)$ ,  (22)

Where is the free energy and is the reciprocal temperature value $\beta =1/T$ . Condition (21) allows us to determine the non-operator part of Hamiltonian (19):

$E_0=2\left(c-\tilde{c}\right){\displaystyle \sum _k\hslash k{f}_k}+{\displaystyle \sum _k\hslash ck}+\langle H_I\rangle$   (23)

where the distribution function of renormalized photons has the Planck form

$f_k=\langle a_{kj}^{+}{a}_{kj}\rangle =\frac{1}{\exp \left(\beta \hslash {\tilde{\omega }}_k\right)-1}$   (24)

and does not depend on the polarization index. From the normalization condition of the statistical operator (22) $\text{Sp}\rho \text{=1}$  follows the expression for the free energy of radiation

$F=2\left(c-\tilde{c}\right){\displaystyle \sum _k\hslash k{f}_k}+{\displaystyle \sum _k\hslash ck}+\langle H_I\rangle +2T{\displaystyle \sum _k\ln \left(1-e^{-\beta \hslash {\tilde{\omega }}_k}\right)}$ .  (25)

If we neglect the photon-photon interaction and zero-point fluctuations, formula (25), follows the usual formulas of the thermodynamics of black radiation. It is natural to require that in the approximation used with Hamiltonian (19) and free energy (25), as in the case of a gas of non-interacting photons, thermodynamic relations must be satisfied. Since the introduced renormalized speed itself, in principle, can depend on thermodynamic variables to satisfy the thermodynamic relations, the following condition must be met:

$\frac{\partial F}{\partial \tilde{c}}=0$ .  (26)

From this condition and formula (25) follows the relationship that determines the renormalized speed:

$\tilde{c}-c=\frac{\frac{\partial \langle H_I\rangle }{\partial \tilde{c}}}{2\frac{\partial }{\partial \tilde{c}}{\displaystyle \sum _k\hslash k{f}_k}}$   (27)

Since (27) includes the temperature-dependent distribution function (24), then, naturally, the speed of light is a function of temperature. Thus, the average of the interaction Hamiltonian should be calculated. In this case, as in the theory of phonons in solids, divergent integrals appear. When describing phonons within the continuum model, it is natural to cut off such integrals at a wave number equal to the inverse of the average distance between particles or, when integrating over frequency, at the Debye frequency. In the case of photons, the divergent integrals will be cut off at the wave number, the choice of which will be discussed a little later.

Taking this into account, calculating the average of the interaction Hamiltonian (13) gives

$\langle H_I\rangle =\frac{1312V}{15{\pi }^2}D\cdot {\hslash }^2{c}^2\cdot J\left(\frac{k_m^4}{4}+J\right)$   (28)

where, $J=6\zeta \left(4\right){\left(\frac{T}{\hslash \tilde{c}}\right)}^4$ , $\zeta \left(4\right)={\pi }^4/90\approx 1,0823$  is the zeta function. Let be the ratio of the temperature-dependent speed of light to the “base” speed of light. Considering that ${\displaystyle \sum _k\hslash k{f}_k}=\frac{V\hslash }{2{\pi }^2}J,$ from (27), we find the equation for:

$\sigma =1+\frac{328}{15}D\cdot \hslash c\cdot k_m^4+\frac{328\cdot 16}{5}\zeta \left(4\right)D\cdot \hslash c{\left(\frac{T}{\hslash c}\right)}^4\cdot \frac{1}{{\sigma }^4}$   (29)

It follows that the ratio of the speed of light at zero temperature ${\tilde{c}}_0$  to the “primary” speed of light ${\sigma }_0\equiv {\tilde{c}}_0/c$ is determined by the formula:

${\sigma }_0=1+\frac{328}{15}D\cdot \hslash c\cdot k_m^4$   (30)

The directly measurable speed is the speed of light at zero temperature. As follows from (30), this speed does not coincide with the “primary” speed of light due to taking into account the interaction of photons. Due to the weakness of this interaction, should differ very little, and in the leading approximation they could be considered equal, which would not affect subsequent conclusions.

Experiments show that if an external field acts on the vacuum, then due to its energy, the production of fundamental particles is possible.¹² Precisely because the vacuum is not virtual, but a natural physical object (dark matter) and has a structure, the polarization of the vacuum leads not to virtual, but natural radiation corrections to the laws of quantum electrodynamics.¹² The interaction of the electromagnetic field with the vacuum (dark matter) leads to a dependence of the speed of light propagation on the radiation temperature. Estimates show that in the modern era, even at very high temperatures, such as those that exist in the bowels of stars, the temperature-dependent correction to the speed of light is minimal:¹²

$\Delta \tilde{c}=\tilde{c}-c_0\approx {10}^{-5}cm/s$   (31)

Where ∆c is the temperature-dependent correction to the speed of light,

с is the speed of light in the interior of a star,

с₀ is the speed of light in the space vacuum.

 However, in the cosmological model of the hot Universe, in the first moments after the Big Bang, the temperature was so high that the speed of light was many orders of magnitude higher than the modern one. The effect of the dependence of the speed of light on temperature should be essential for understanding the early evolution of the Universe. As a result, Dr. Yuri Poluektov obtained a dependence for the fine structure constant, recorded through the observed speed of light:¹²

${\alpha }_0\equiv \frac{e^2}{\hslash {\tilde{c}}_0}$   (32)

With the expansion of the Universe and its cooling, the speed of light decreased and has now reached its value, almost equal to the speed of light at zero temperature. At Planck's temperature, Tp ≈1.42×10³²[K] ≈ 10¹⁹[GeV], the speed of light ${\tilde{c}}_p$ would be much higher than the modern one (Table 1):

${\tilde{c}}_p/{\tilde{c}}_0\approx 0.8\cdot {10}^{17}$   (33)

The reason for the large effect immediately after the birth of the universe during weak photon-photon interaction, as can be seen from the penultimate column of the table, is the extremely high density of photons at such temperatures.¹² Einstein was very interested in proving the possibility of the dependence of the speed of light on external conditions. According to the memoirs of P.L. Kapitza,¹³ when he, working in the 30s of the last century at Rutherford's Cavendish Laboratory, obtained magnetic fields 10 times stronger than those obtained before him, a number of scientists advised him to conduct experiments to study the effect of a strong magnetic field on the speed of light . Einstein suggested this most insistently. He spoke to P.L. Kapitsa: "I do not believe that God created the universe in such a way that the speed of light does not depend on anything in it." And yet P.L. Kapitsa refused the proposed experiment, on the grounds that the experiment promised to be extremely complex, and the effect, if it were discovered, would certainly be on the verge of the accuracy of the experiment, and there would be no confidence in these results. The above calculations of the dependence of the speed of light on temperature allow us to definitely state that, as Einstein suggested, the magnetic field, as well as temperature, will affect the speed of light propagation. Professor Poluektov estimated the order of magnetic fields, at which the speed of light will change significantly, as H=10¹⁶Gs. Therefore, P.L. was also right. Kapitsa, refusing to conduct a laborious experiment, since the fields necessary to observe such an effect must be so large that they can hardly be realized under modern conditions. Based on formulas (2) and the dynamics of changes in the value of the speed of light, as the Universe cools, it is possible to estimate the dynamics of changes in the value of the fine structure in the process of evolution of the Universe. Professor A.V. Rykov RAS, Institute of Physics of the Earth, relying on his theory of vacuum, as well as the energy of polarization of the vacuum and its electromagnetic parameters (ε₀, μ₀), calculated the value of the fine structure of the near-Earth quantum vacuum (dark matter) and intranuclear quantum vacuum. According to him, the fine structure of the near-Earth quantum vacuum αₑ = 0.0072975 or (1/137) and the fine structure inside the hydrogen nucleus αₓ = 0.00318157 (1/314) determine electromagnetism in the first case, and nuclear forces in the second case.¹⁴ The Professor A.V. Rykov determined the elastic deformation force in near-Earth quantum vacuum F=1.155 ×10¹⁹ [kg / s²] and inside the proton nucleus F=5.211×10²⁶ [kg / s²]. Thus, the elasticity of quantum vacuum inside the nucleus is 7 orders of magnitude higher than that of near-Earth quantum vacuum (dark matter).¹⁴ In 2018 Prof. Volker Burkert conducted a series of experiments at the CEBAF accelerator. After the collision of fast electrons with a mass of liquid hydrogen (the source of protons), the researchers registered the particles resulting from their interaction - an electron, a proton and two photons. This made it possible for the first time to measure the pressure at the center of a proton by bombarding the proton with electrons whose energy reached 100 MeV or more, which allowed the electron to penetrate into the structure of the proton.¹⁵ Volker Berkert and his colleagues at Jefferson's laboratory found that the pressure in a proton can exceed 10³⁵ Pascal.¹⁵ It is known that at such a pressure, polarization of the quantum vacuum and an increase in the value of the fine structure constant by the value indicated by Professor Rykov inside the hydrogen nucleus αₓ = 0.00318157 (1/314) are observed. In an article by astrophysicists from Finland, published on June 1, 2020, it is said that “the matter inside the most massive stable neutron stars is interpreted as evidence of the presence of nuclei of quark matter, in which the speed of sound almost reaches the speed of light”.¹⁶ A form of this strange substance, called quark-gluon plasma, is believed to have filled the newborn universe about 20 microseconds after the Big Bang. It behaved like an extremely hot liquid, which then cooled down to the state of "ordinary" matter that fills the universe today.¹⁶ At present, the only place in the universe where quark matter can still be found is at the epicenter of particle collisions at the Large Hadron Collider and possibly the heart of a neutron star. It is in neutron stars that nuclear forces determine the value of the fine structure, which is αₓ = 0.00318157 (1/314). Moreover, the force of confinement of quarks in the core of a neutron star is F = 5.211 × 10²⁶ [kg/s²]. The vacuum polarization effect leads to charge screening at low energies. With increasing energy, acceptable structure magnitude (α) changes logarithmically:

$\alpha \left(E\right)= \frac{{\text{α}}_{\text{0}}}{1-\Delta \text{α}\left(\text{E}\right)}$   (34)

Where E is the electric field strength,

∆ α is the incremental value calculated as part of QCD

 Recent research by scientists from Boston University, the Massachusetts Institute of Technology (MIT) and the Max Planck Institute has investigated the fine structure constant that occurs in systems with condensed matter. Their article “The emerging fine structure constant of quantum spin ice is large” was published in Physical Review Letters in 2021.¹⁷ Condensed matter systems provide an alternative "vacuum" that exhibits emerging low-energy properties that differ sharply from those of the standard model. A case in point is emerging quantum electrodynamics (QED) in a fractionated topological magnet known as quantum spin ice, whose magnetic monopoles distinguish it from the familiar QED world we live in. According to calculations, inside the quantum spin ice, the constant that determines the electromagnetic interactions is 10 times greater than the normal one.¹⁷ The term quantum spin ice (QSI) simultaneously refers to a family of models as well as to a class of rare earth magnetic materials that approximate the theoretical models. Thus, the increase in the fine structure value, noted in new studies,¹⁷ in addition to nuclear interactions in QED and QCD also in quantum spin ice, means that these condensed systems can be ideal for studying physical phenomena arising as a result of strong particle interactions. Thus, the value of the fine structure is determined by five fundamental interactions: electromagnetic, gravitational, strong and weak nuclear interactions and the fifth interaction between baryon matter and quantum vacuum (dark matter) and their derivatives: temperature, pressure and polarizations of the physical vacuum.

Newton's gravitational constant G₀ and vibrational paradoxes Academicians Pyotr Kapitsa and Vladimir Chelomey

Experiments on the measurement of the gravitational constant G, carried out in recent years by several groups, show a striking discrepancy with each other. For the first time, the gravitational constant G, which is part of Newton's law of universal gravitation, was measured in 1798 by the British experimental physicist Henry Cavendish. For this, the scientist used a torsion balance. The value obtained by Cavendish for the constant was G = 6.754×10¯¹¹H⋅m²⋅kg, and the relative error of the experiment did not exceed one percent. The recently published new measurement, made at the International Bureau of Weights and Measures, is different from all and only exacerbates the problem. The gravitational constant remains an extremely stubborn value for accurate measurement, despite more than two hundred years of history, the accuracy of measurements remains very modest. The current "official" value of the gravitational constant G recommended by the US National Institute of Standards (NIST) is (6.67384 ± 0.00080) ⋅10¯¹¹ m³⋅kg¯¹⋅s¯² . The relative error here is 0.012%, or 1.2×10¯⁴, or, in even more familiar notation for physicists, 120 ppm (millionths), and this is several orders of magnitude worse than the measurement accuracy of other equally important quantities. Moreover, for several decades now, the measurement of the gravitational constant has not ceased to be a source of headache for experimental physicists. Despite dozens of experiments carried out and the improvement of the measuring technique itself, the measurement accuracy remained low. A relative error of 10¯⁴ was reached 30 years ago, and there has been no improvement since then. The situation when four or five results at once, obtained by different groups, all differ by a dozen or two declared errors, is apparently unprecedented for physics. No matter how high the accuracy of each measurement and no matter how proud the authors may be, it is now of no importance for establishing the truth. And for now, trying to find out on their basis the true value of the gravitational constant can only be done in one way: put the value somewhere in the middle and attribute an error that will cover this entire interval (that is, worsen the current recommended error by a factor of one and a half or two). “One can only hope that the next measurements will fall into this interval and will gradually give preference to any one value. One way or another, but the gravitational constant continues to be a puzzle of measurement physics. In how many years (or decades) this situation will really begin to improve, it is now difficult to predict”.¹⁸ I assume that the reason for the striking discrepancy between the values ​​of the gravitational constant in various experiments is not the organization of experiments and the quality of the equipment, but the dependence of the gravitational constant on the frequency of the Earth's oscillations as it rotates around its own axis and hope that the next measurements will give stable values, not really. Professor A.L. Dmitriev believes that independent measurements of high-frequency (in the range of hundreds of thousands of Hz) spectra of oscillations of the Earth's gravity, performed using superconducting gravimeters, will make it possible to determine the modes of coordinated oscillations of oscillators. He found that when measuring Δg the average value of the acceleration due to gravity, the sign of Δg is directly determined by the phase difference Ѳ of the oscillations between the Earth's gravity and the oscillator. This leads to a significant increase or decrease in the average gravity acting on the mechanical oscillator from the Earth's variable gravitational field. This effect can become the basis for creating technical systems for overcoming gravity and a new principle for controlling the movement of bodies.¹⁹ The alternative theory of Modified Newtonian Dynamics (MoND) has proven its applicability in galaxies, where the violation of Newton's laws occurs at extremely low accelerations characteristic of galaxies in the absence of dark matter, but much less than anything that is commonly found in the solar system or on Earth. In this case, the strong equivalence principle in MOND is violated.²⁰ In the pendulum of academician Peter Kapitza, whose axis oscillates vertically, the load moves against the forces of gravity, and at the same time produces more energy than is consumed to maintain vertical vibrations and overcome friction losses during pendulum oscillations.²¹ The influence of the medium in the nonequilibrium state of the pendulum determines the origin of the kinetic effective mass Meff(ν,α), which depends on the frequency ν and the amplitude of the pendulum and is associated with the excitation around the pendulum, in which the attachment point moves with frequency ν in a continuous medium, the field of hydrodynamic velocities υᵢ (r ). In this regard, additional kinetic energy appears, leading to an increase in the inertial mass of the pendulum, which in turn leads to a violation of the principle of mass equivalence. As Peter Kapitsa noted, pendulum clocks on a vibrating base are always in a hurry.⁵ This can be explained by the violation of the equivalence principle, since the kinetic energy can be much greater than the potential energy. Based on the vibrational paradoxes of Academician Vladimir Chelomey, including experiments with vibrating liquids in which steel balls float and a pendulum in which the load rises up on a vibrating rod, it was possible to come close to creating a physical model of a levitating body.²² I propose to develop and improve the principles of controlling the movement of bodies within the framework of research work on the basis of vibrational paradoxes of academician V. Chelomey. As in the pendulum of Kapitsa, in the pendulum of Chelomey, the dynamic potential field, which, superimposed on the gravitational field of the Earth, generates the so-called effective potential. The complex force F(ν) does work by lifting the weight of the pendulum against the force of gravity to the maximum possible height. In addition to the centrifugal force, it includes the force from the environment, which affects the non-equilibrium system of the Chelomey pendulum. This is the effect in which the hydrodynamic effect on spherical bodies of any nature in liquid and gas that oscillate was declared by Stokes two centuries ago. This effect was experimentally tested in a plasma environment superfluid ³He-B by Vladimir Shikin, an employee of the Institute of Solid State Physics, Russian Academy of Sciences, in 2013. We are talking about a complex force F (ω) acting from a liquid on a sphere of radius R, performing periodic oscillations with a frequency ω. Within small Reynolds numbers, we have:²³

$F(\omega )=6\pi \eta R\left(1+\frac{R}{\delta \left(\omega \right)}\right)V(\omega )+3\pi R²\sqrt{ \frac{2\eta \rho }{\omega }}\left(1+\frac{2}{9}\frac{R}{\delta \left(\omega \right)} \right)i\omega V\left(\omega \right),$   (35)

δ (ω) = (2η/ρω)½

where ρ - fluid density, η – viscosity, V - velocity amplitude sphere, δ (ω) - the so-called viscous penetration depth, which increases with an increase in viscosity and a decrease of the oscillation frequency.

$Мeff \left(\omega R\right)=\frac{2\pi \rho R³}{3} \left[1+ \frac{9}{2} \frac{\delta \left(\omega \right)}{R}\right]$   (36)

The real part of expression (35) is the known Stokes force that arises when a sphere moves in a liquid. It is natural to identify the imaginary component (coefficient at iωV) with the effective additional mass Meff(ν,α). In a superfluid liquid, the additional mass has two components: superfluid and normal.²³ V.N. Chelomei did not have time to complete the work with his pendulums. Judging by the differential equations, they do not take into account centrifugal forces, but take into account the influence of the medium in which the pendulum oscillates.

Thus, the meaning of the fine structure is determined by five fundamental interactions: electromagnetic, gravitational, strong and weak nuclear interactions and the fifth interaction between baryonic matter and quantum vacuum (dark matter) and their derivatives: temperature and pressure. Vacuum is involved in all fundamental interactions, but if the polarization of the vacuum in electromagnetic interactions is accompanied by the formation of electron-positron pairs with the participation of exchanged virtual photons, then in nuclear interaction the polarization of the quantum vacuum is accompanied by the formation of three unstable π-mesons (π⁰, π +, π-) with the participation of virtual exchange pions and the subsequent creation of short-lived protons and antiprotons. At the same time, the energy spectrum of the birth of new particles and antiparticles changes, which indicates a difference in the structure of the quantum vacuum when it is included in the nuclei of atoms.15 Professor Anatoly Rykov called the medium of virtual pi-mesons, participating as exchange particles in atomic interactions, the meson ether. If we assume that the meson structure of the ether is formed by a triple of pions π⁰,π⁺,π⁻ should be held by a force corresponding to the value of the nuclear fine structure, then it will exceed the value of the fine structure of the physical vacuum, which has an electron + positron pair. This corresponds to reality.¹⁵

None.

None.

1. Kosinov NV. Laws of the unitron theory of physical vacuum and new fundamental physical constants. Phys Vacuum Nat. 2000;n3. 
2. Gilbert L. New findings suggest laws of nature 'downright weird,' not as constant as previously thought. University of New South Wales. 2020.
3. Konstantinov S. The role of vacuum polarization in the large hadron collider. Global J. 2020;20(4)21–27.
4. Barton G. Faster-than-c light between parallel mirrors. The Scharnhorst effect rederived. Phys Lett. 1990;237(3–4):559–562.
5. Barlow R. The conversation- has cern discovered a particle that 'threatens our understanding of reality?  Sci Technol. 2018.
6. Physics news. Running mass of a τ–quark. Physics- Uspekhi. 2019;62(11):1172.
7. Migkas K, Schellenberger G, Reiprich TH, et al. Probing cosmic isotropy with a new X–ray galaxy cluster sample through the LX−T scaling relation. A&A. 2020;636:42.
8. Krasznahorkay AJ, Csatlós M, Csige L, et al. Observation of anomalous internal pair creation in ⁸Be: a possible signature of a light, neutral Boson. Phys Rev Lett. 2016;116:042501.
9. Eroshenko YN. Physics news on the internet. Particle X17. Physics- Uspekhi. 2020;63(1):112.
10. Jonathan LF.  Protophobic fifth force interpretation of the observed anomaly in ⁸Be nuclear transitions.  Phys Rev Lett. 2016;1:6.   
11. Wilczynska MR, Webb JK, Bainbridge M, et al. Four direct measurements of the fine structure constant 13 billion years ago. Sci Adv. 2020;6(17):9672.
12. Yu. MP. On the dependence of the equilibrium light speed on the temperature. National Science Center Kharkov Institute of Physics and Technology. 2019.
13. Kapitsa PL. Experiment, theory, practice. M. Nauka 1974;288p.
14. Burkert VD, Elouadrhiri L, Girod FX. The pressure inside the proton. Nature. 2018;557(7705):396–399.
15. Rykov AV. Fundamentals of the theory of ether. Moscow: Russian Academy of Sciences, Institute of Physics of the Earth. 2000.
16. Annala E, Gorda T, Kurkela A, et al., Evidence for quark–matter cores in massive neutron stars. Nat Phys. 2020;16:907–910.
17. Pace SD, Morampudi SC, Moessner R, et al. Emergent fine structure constant of quantum spin ice is large. Phys Rev Lett. 2021;127:117205.
18. Quinn T, Parks H, Speake C, et al. Improved determination of G using two methods. Phys Rev Lett. 2013;111:101102.
19. Dmitriev AL. Experimental gravity. St. Petersburg: Renome. 2014.
20. Mordecai M. MOND laws of galactic dynamics. Royal Astronomical Society Monthly Notices. 2014;437(3):2531–2541.
21. Kapitsa P.L. Pendulum with a vibrating suspension. UFN. 1951;44(1)7–20.
22. Chelomey VM. Paradoxes in mechanics caused by vibrations. Acta Astronautica. 1984;11(5):269–273.
23. Shikin V. Low- frequency anomalies of effective mass of charged clusters in liquid helium. Low Temp Phys. 2013;39(10):837–841.