In vibration/noise control engineering, mutual effects of vibration and sound are of considerable importance for accurate and realistic design of cavity systems composed of solids and fluids. The integrated Finite Element Method/Boundary Element Method (FEM/BEM) approach is a convenient vibro-acoustic tool for coupling of the two media. This study implements a FEM/BEM model for a box-like cavity under structural and acoustical excitations. The prominent coupled response characteristics of the model subjected to harmonic, periodic, almost periodic and random forces are examined with engineering aspects. The effects of random forcing and harmonic forcing are compared with regard to both vibration and sound responses. This comparison is extended to response analysis of the system to structural and acoustical forces.

Keywords: vibro-acoustics, structural-acoustic coupling, FEM/BEM

When an enclosure bounded by thin walls is subjected to a structural and/or acoustic excitation, a coupling phenomenon occurs due to the mutual interaction between the vibration and sound. The physical coupling between the structure and fluid in the enclosure reflects to the mathematical coupling between the equations of motion. The matrix solution of these coupled equations puts forward the vibration characteristics of the structure under the fluid loading and the acoustic features of the fluid subjected to vibration. This is a sensitive solution representing the mutual effects of vibration and sound.

The behaviour of sound in small volumes and vibration of volume walls are fundamental subjects for vibration and noise control engineers. Small volumes have many industrial applications such as vehicle cabins, transportation containers and liquid tanks. Therefore, vibro-acoustic behaviour of cavity-type structures has been examined since many years by different methods and from different points of view. Firstly, Lyon,¹ has made a theoretical study on the noise attenuation of a box with one flexible wall. Pretlove,² has developed a mathematical model and compared the model’s solutions with the experimental results for free vibrations of a flexible panel-cavity system. Then, Pretlove,³ has examined the response of systems under the excitation of external random acoustic pressures. Guy and Bhattacharya,⁴ have analysed theoretically and experimentally the coupling effect of a cavity-plate system on the sound transmission and vibration of the plate; and concerned with the negative transmission loss, combined panel and cavity resonance. Dowell et al.⁵ have established a theoretical model for interior sound fields with a flexible wall under the excitation of exterior sound fields; and compared the theory with experiments.

The problem of vibro-acoustic coupling requires very sensitive models. Therefore, the progress of computers and the related developments in numerical techniques have improved the coupling analysis. Finite element method (FEM), boundary element method (BEM) or hybrid methods made possible the solution of today’s structures with complex geometries. Zienkiewicz and Newton,⁶ have solved fluid-structure interaction problems using finite elements to represent both the structure and the fluid. Craggs,⁷ has examined the coupled systems first by using finite elements for both parts; then using the finite element method for the structure and volume displacement theory for the fluid.⁸ Sestieri et al.⁹ have used Helmholtz integral equation formulation for the analysis of structural-acoustic coupling in complex shaped cavities. Mariem and Hamdi,¹⁰ have developed a boundary finite element method; and found noise transmission loss factor and dominant modes in this phenomenon. Everstine,¹¹ has reviewed finite element formulations used to solve structural acoustics and fluid-structure interaction problems. Vlahopoulos et al.¹² have presented a coupled solution combining structural FEM and indirect BEM for structural-acoustic models. Ding and Chen,¹³ have established a symmetrical finite element model for structural-acoustic coupling analysis; and validated the correctness of their method experimentally. Lee,¹⁴ has studied structural-acoustic coupling of a rectangular box, by using a finite element modal method for large amplitude of vibrations of the flexible plate. Li and Cheng,¹⁵ have used a combined integro-modal approach to examine a vibro-acoustic model composed of a flexible panel backed by a cavity with a tilted wall. Dhandole and Modak,¹⁶ have presented an improvement for the vibro-acoustic finite element models of weakly coupled cavities. Park et al.¹⁷ have examined the effect of local stiffeners in the structural-acoustic coupled systems. Genechten et al.¹⁸ have presented a hybrid simulation technique applying a wave-based model for the acoustic cavity and a direct finite element model for the structural part. Xie et al.¹⁹ have developed a variational based method to make a response study of a coupled system including an irregular cavity with general wall impedance and a flexible panel subjected to arbitrary edge-supporting conditions. Shi et al.²⁰ have examined a coupled system consisting of a partially opened cavity coupled with a flexible plate and a semi-infinite exterior field.

The present study intends to put forward the practical engineering aspects of structural-acoustical coupling with regard to response behaviour of cavity-type structures. A box with a flexible wall is used as a simplified model. An integrated Finite Element Method/ Boundary Element Method (FEM/BEM), FEM for the solid box and BEM for the interior fluid, are implemented. Response characteristics of this system to different structural and acoustical excitations are examined. Results are discussed on the basis of both companions of the coupling phenomenon, vibration and sound.

If vibro-acoustic coupling between the structure and fluid is neglected, the solution is performed at two sequential stages. Initially, vibration of the structure and then sound radiation caused by the structural vibration are considered. However, in coupled systems vibration and acoustic equations are solved simultaneously.

When harmonic vibration of a structure is described by the finite element method, the vibration equations under acoustic loading may be written in the following form,

$\left[-{\omega }^2\left[M\right]+i\omega \left[C\right]+\left[K\right]\right]\left\{d\right\}=\left\{f_e\right\}-\left[G_c\right]\left\{p\right\}$   (1)

Here, w is the radian frequency, i=Ö-1 is the complex number, [M], [C] and [K] are the structural mass, damping and stiffness matrices respectively. {d} is the nodal structural displacement vector, {f_e} is the external force vector applied to structural nodes, [G_c] is the transformation matrix including surface area induced by the acoustic pressures, {p} is the acoustic pressure vector., [G_c]{p} product represents the additional structural loading created by the acoustic pressure field on the structure.

When the boundary element method is implemented to predict the acoustic field near the vibrating structure, the following system of equations is obtained:

$\left[L\right]\left\{p\right\}=\left[H\right]\left\{u_n\right\}$   (2)

Here {u_n} is the nodal normal velocity vector, [L] and [H] are square matrices. On the other hand, the momentum equation is written as,

${\rho }_0\frac{\partial u}{\partial t}=-\nabla p$   (3)

Where u, is the acoustic particle velocity and ρ₀, is the density of the fluid in the medium. Assuming a harmonic change for the particle velocity ($u=U{e}^{i\omega t}$ ) Eq. (3) may be rewritten as,

$\frac{\partial p}{\partial n}=-i{\rho }_o\omega u_n$  (4)

By using Eq. (4), Eq. (2) may be written as,

$\left[L\right]\left\{p\right\}+\left[R\right]\left\{\frac{\partial p}{\partial n}\right\}=0$   (5)

Where $\left[R\right]=-\frac{i}{{\rho }_0\omega }\left[H\right]$ . Since $u_n=i\omega d$ , boundary element equation (5), with an acoustic excitation may be written as,

$\left[L\right]\left\{p\right\}+{\rho }_0{\omega }^2\left[R\right]\left\{d\right\}=\left\{q_e\right\}$   (6)

Finally, the integrated FEM/BEM matrix equation may be written in the following form,

$\left[\begin{array}{cc}\left[K\right]+i\omega \left[C\right]-{\omega }^2\left[M\right]& \left[G_c\right]\\ {\rho }_0{\omega }^2\left[R\right]& \left[L\right]\end{array}\right]\left\{\begin{array}{c}d\\ p\end{array}\right\}=\left\{\begin{array}{c}{f}_e\\ q_e\end{array}\right\}$   (7)

Homogenous form of Eq. (7) is used in the prediction of coupled natural frequencies ${\omega }_i$ with their corresponding mode shapes.

The integrated FEM/BEM method yields accurate solutions for especially thin-walled structures and interior fluids. This approach utilizes known superiorities of each method: FEM’s symmetrical matrices and less computation time whereas BEM’s two-dimensional models and less modelling time.

Vibro-acoustic characteristics

In this study, the cavity is in the shape of a box with dimensions 60 mm X 310 mm X 310 mm as shown in (Figure 1). The box is composed of thin steel walls with a thickness of 0.5 mm. These walls are connected to each other satisfying clamped boundary condition. One of the walls is flexible and the others are rigid. The box is full of air. The physical parameters of steel are; density $\rho$ =7900 kg/m³, modulus of elasticity E =2.1x10¹¹ N/m², Poisson’s ratio $\mu$ =0.3. The physical parameters of air are; density ${\rho }_0$ =1.2 kg/m³, speed of sound c =340 m/s.

The validity of the proposed FEM/BEM model was examined for various sizes and meshes of plate-cavity systems on the basis of the comparisons of numerical natural frequencies with the analytical counterparts.²² It was determined that 32 X 32 meshes for structural modes and 16 X 32 X 32 meshes for cavity and coupled modes were optimal sizes from the point of view of the sensitivity requirement and computation time. Although, this paper is mainly devoted to vibro-acoustic response characteristics of cavity-type structures, natural frequencies of the present system were also calculated and presented to make a detailed analysis of the phenomenon. The first ten structural natural frequencies of the flexible plate and the first two cavity frequencies are shown together with the coupled natural frequencies of the system in (Table 1). The cavity depth of the present model (60 mm) is less than the one quarter of the larger dimension of the plate (310/4=77.5 mm). Pretlove,² has shown that if the plate-cavity system has such geometry, a stiffening effect of the cavity emerges. Therefore, the uncoupled fundamental mode frequency of the plate increases in the coupled case. However, the coupling with plate vibration makes also a stiffening effect on the cavity frequency.

Response characteristics of the system are examined for five different types of excitation. These are harmonic, periodic, almost periodic, random structural excitations and also a combination of random structural and acoustical excitations. All frequency spectra are presented for the response point at the centre of the one-quarter of the plate as shown in (Figure 2). Response variables are computed in terms of decibel (dB) by using reference values a_ref =9.81 m/s² for the acceleration and p_ref = 2 $\times$ 10^-5 Pa for the acoustic pressure.

Structural harmonic excitation

Flexible plate is excited by two structural harmonic forces with 10N magnitude at the centre sequentially. The first excitation frequency is 46 Hz, equal to the fundamental structural frequency; the second forcing frequency is 92 Hz, equal to the fundamental coupled frequency. Excitation forms are, $F=10\sin (2\pi \times 46t)$ and $F=10\sin (2\pi \times 92t)$ , respectively. Acceleration and sound pressure response spectra for these excitations are presented in (Figure 3), in 10 Hz frequency bands. As it is expected, the responses arise at the excitation frequencies, 46 Hz and 92 Hz. However, both the vibration and the sound response at the fundamental structural mode (46 Hz) are higher than those at the fundamental coupled mode (92 Hz). This is an apparent consequence of the stiffening effect of the plate-cavity system. Since the coupled system is of the stiffened type, it behaves more rigidly at the coupled frequency compared to the uncoupled system at the structural frequency.

Structural excitation with two harmonics

Structural excitation is performed by two superimposed 10 N-harmonic force acting to the centre of the plate. As shown in the mode shapes of a square clamped plate in (Table 2), the nodal lines don’t pass through the centre of the plate in the first and fifth modes. Therefore, these modes are more affected by the structural forces applied to the centre. For this reason, the periodic force for the uncoupled case is formed by the frequency components corresponding to the first (46 Hz) and fifth (170 Hz) modes. For the coupled case, the corresponding frequencies are 92 Hz and 180 Hz, respectively. The time behaviour of superimposed forces is shown in (Figure 4). For the uncoupled case, the resultant is a periodic force with 50 Hz-frequency. The second superimposed force has almost periodic characteristics with a fundamental frequency of 91 Hz.

The acceleration and sound pressure response spectra are presented in (Figure 5). Although three modes of the spectra show overall damping effect of coupling, there is one exception. The coupled first peak acceleration is higher than the uncoupled one. This is near resonance behaviour, since in the coupled analysis the fundamental forcing frequency (91 Hz) is very close to the fundamental natural frequency (92 Hz).

Random excitations

Random excitations are examined as structural, and a combination of structural and acoustical excitations.

Random structural excitation

A random structural force with constant 10 N-amplitude through the considered frequency range (40Hz – 600 Hz), is acted to the centre of the plate. Uncoupled, coupled acceleration and sound pressure response spectra are presented in (Figure 6). The uncoupled response peaks correspond to the structural modes of the plate. The excited modes are those that have no nodal lines through the centre (1_st, 5_th, 7_th, 13_th and 17_th). The first cavity mode in this frequency range cannot be excited. The significant effect of the random excitation is to increase the first acceleration peak of the coupled response. The damping effect of coupling is apparent for the other modes of acceleration and for all modes of the sound pressure.

Random structural and acoustical excitations

The plate cavity system is excited by the previous structural force with constant 10 N-amplitude, and a monopole with source strength $Q=10m^3/s$ as an acoustic source. This loading system is shown in Figure 1. Acoustic source has the same spectral characteristics with the structural force. Acceleration and acoustic pressure responses presented in (Figure 7) show prominent characteristics due to the effect of the monopole source. Firstly, in addition to the first coupled mode of vibration the first sound peak also increases. Secondly, new uncoupled and coupled modal peaks form towards the higher frequencies. The uncoupled one is at 552.41 Hz and emerges in the sound response spectrum. The coupled modes of vibration response occur at 548.73 Hz, 569.6 Hz and 587 Hz frequencies, whereas sound response at 540.6 Hz, 569.6 Hz and 588.6 Hz frequencies. These new modes appear in the form of peak families. The coupled peak at 569.6 Hz is the mode corresponding to the first cavity mode and arises both in vibration and sound responses as a dominant component.

(Table 3) shows the overall root mean square (RMS) sound pressure responses for both uncoupled and coupled analyses. It is seen that the addition of acoustical source does not create an observable increase in the response for the uncoupled analysis. However, coupled analysis puts forward the meaningful rise of the response due to the effect of the acoustical source. On the other hand, the overall impact of the coupled analysis is lowering the sound pressure response. The lower RMS values in the coupled analysis are indicators of the energy loss in the system due to the sound attenuation effect of the present cavity.

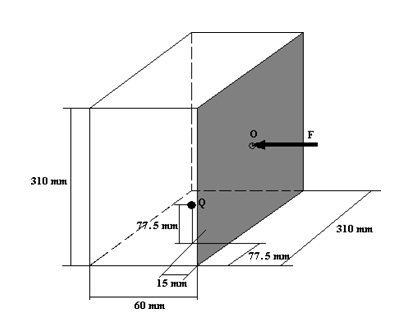
Figure 1 Mechanical and acoustical excitations acting to the box model, F: Structural excitation, Q: Monopole source.

Figure 2 Location of the response point.

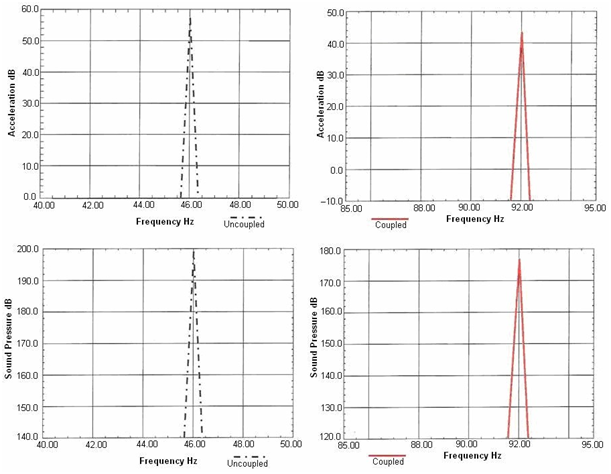
Figure 3 The uncoupled, coupled accelerations and sound pressure responses of the plate- cavity system to structural harmonic excitation.

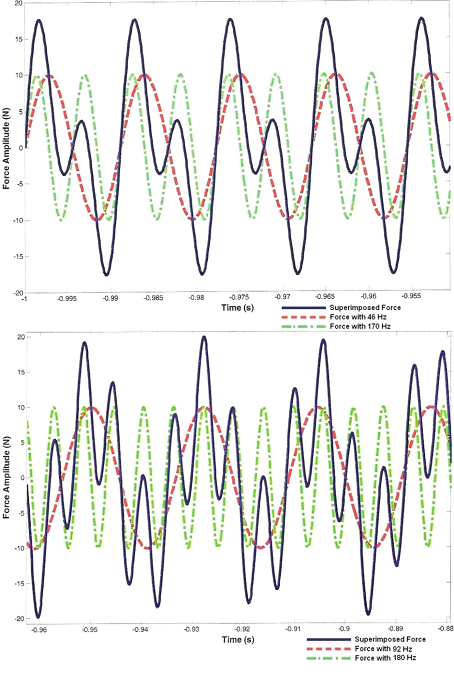
Figure 4 (A) Periodic behaviour of the superimposed force composed of harmonics at 46 Hz and 170 Hz, (B) Almost periodic behaviour of the superimposed force composed of harmonics at 92 Hz and 180 Hz.

Figure 5 The uncoupled, coupled accelerations and sound pressure responses of the plate-cavity system to structural excitation with two harmonics.

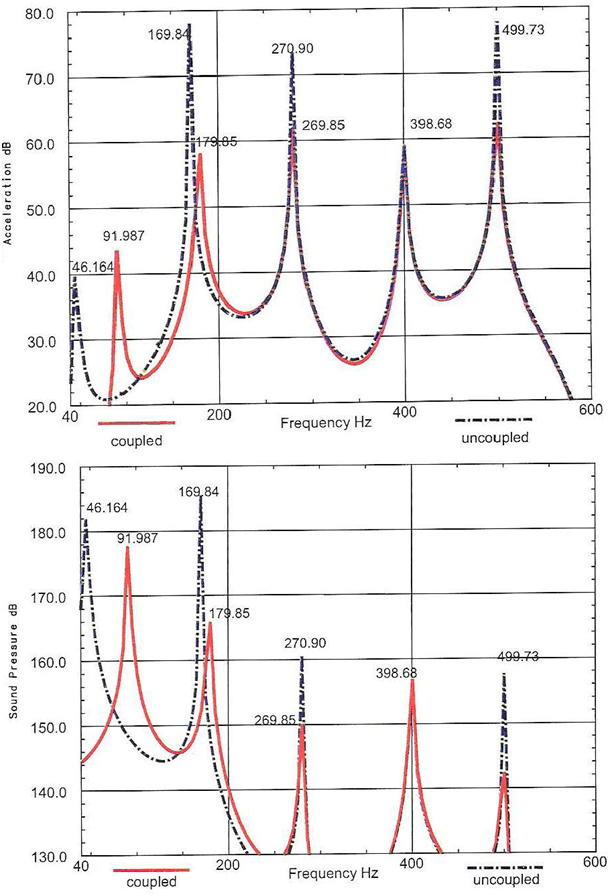
Figure 6 The uncoupled, coupled accelerations and sound pressure responses of the plate-cavity system to random structural excitation.

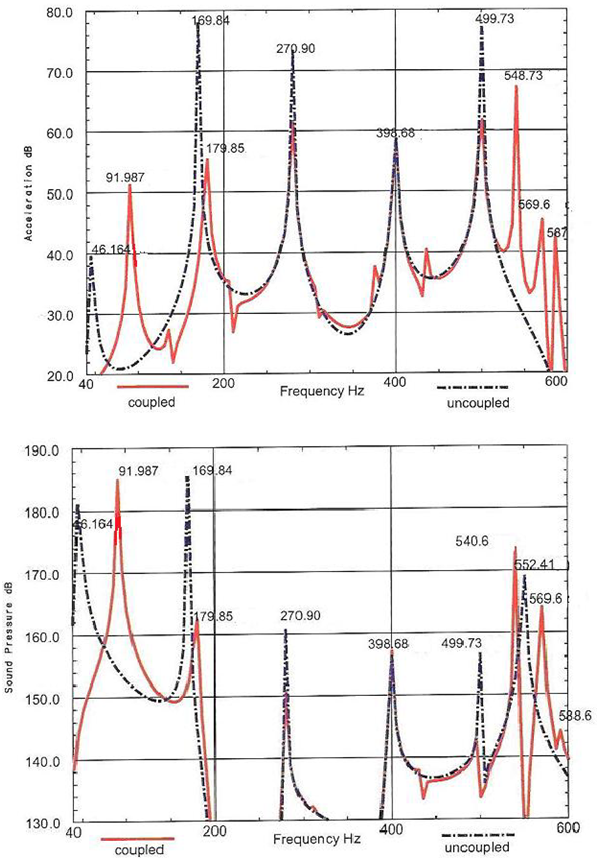
Figure 7 The uncoupled, coupled accelerations and sound pressure responses of the plate-cavity system to random structural and acoustical excitations.

None.

1. Lyon RH. Noisereduction of rectangular enclosures with one flexible wall. J Acoust Soc Am. 1963;35:1791–1797.
2. Pretlove AJ. Free vibrations of a rectangular panel backed by a closed rectangular cavity. J Sound Vib. 1965;2(3):197–209.
3. Pretlove AJ. Forced vibrations of a rectangular panel backed by a closed rectangular cavity. J Sound Vib. 1966;3(3):252–261.
4. Guy RW, Bhattacharya MC. The transmission of sound through a cavity-backed finite plate. J Sound Vib. 1973;27(2):207–223.
5. Dowell H, Gorman GF, Smith DA. Acoustoelasticity:General theory, acoustic natural modes and forced response to sinusoidal excitation, including comparisons with experiment. J Sound Vib. 1977;52(4):519–542.
6. Zienkiewicz OC, Newton RE. Coupled vibrations of a structure submerged in a compressible fluid. Stuttgart: Proc. International Symposium on Finite Element Techniques; 1969:1–9.
7. Craggs A. The transient response of a coupled plate-acoustic system using plate and acoustic finite elements. J Sound Vib. 1971;15(4):509–528.
8. Cragg A. Computation of the response of coupled plate-acoustic systems using plate finite elements and acoustic volume-displacement theory. J Sound Vib. 1971;18(2):235–245.
9. Sestieri E, Del Vescovo D, Lucibello P. Structural-acoustic coupling in complex shaped cavities. J Sound Vib. 1984;96(2):219–233.
10. Mariem JB, Hamdi A. A new boundary finite element method for fluid-structure interaction problems. Int J Numer Meth Eng. 1987;24:1251–1267.
11. Everstine GC. Finite element formulations of structural acoustics problems. Computers & Srrucmres. 1997;65(3):307–321.
12. Vlahopoulos N, Raveendra ST, Vallance C, Scott M. Numerical implementation and applications of a coupling algorithm for structural-acoustic models with unequal discretization and partially interfacing surfaces. Finite Elem Anal.Des. 1999;32:257–277.
13. Ding WP, Chen HL. A symmetrical finite element model for structure-acoustic coupling analysis of an elastic thin-walled cavity. J Sound Vib. 2001;243(3):547–559.
14. Lee YY. Structural-acoustic coupling effect on the nonlinear natural frequency of arectangular box with one flexible plate. Appl Acoust. 2002;63(11):1157–1175.
15. Li YY, Cheng L. Vibro-acoustic analysis of a rectangular-like cavity with a tilted wall. Appl.Acoust. 2007;68(7):739–751.
16. Dhandole S, Modak SV. On improving weakly coupled cavity models for vibro-acoustic predictions and design. Appl. Acoust. 2010;71:876–884.
17. Park SY, Kim SH, Kang YJ. The effect of a local stiffener in the structural-acoustic coupled system. ProcImechE Part C J Mech Eng. Sc. 2010;224:1915–1931.
18. Genechten BV, Vandepitte D, Desmet V. A direct finite hybrid element-Wave based modelling technique for efficient coupled vibro-acoustic analysis. Comput. Meth. Appl. Mech. Eng. 2011;200:742–764.
19. Xie X , Zheng H, Qu Y. A variational formulation for vibro-acoustic analysis of apanel backed by an irregularly-bounded cavity. J. Sound Vib. 2016;373:147–163.
20. Shi S, Su Z, Jin G, Liu Z. Vibro-acoustic modeling and analysis of a coupled acoustic system comprising a partially opened cavity coupled with a flexible plate. Mech. Syst Signal Pr. 2018;98:324–343.
21. Harris CM, Piersol AG. Harris’ Shock and Vibration Handbook. New York: McGraw- Hill; 2002.
22. Arpaz O. Analysis of structural acoustic coupling of plates. Izmir:Dokuz Eylul University; 2006.