This paper investigates a chemically reactive Magnetohydrodynamic fluid flow with heat and mass transfer over a permeable surface taking into consideration the buoyancy force, injection/suction, heat source/sink and thermal radiation. The governing momentum, energy and concentration balance equations are transformed into a set of ordinary differential equations by method of similarity transformation and solved numerically by Runge-Kutta method based on shooting technique. The influence of various pertinent parameters on the velocity, temperature, concentration fields are discussed graphically. Comparison of this work with previously published work on special cases of the problem was carried out and the results are in excellent agreement. Results also show that the thermo physical parameters in the momentum boundary layer equations increase the skin friction coefficient but decrease the momentum boundary layer. Fluid suction/injection and Prandtl number increase the rate of heat transfer. The order of chemical reaction is quite significant and there is a faster rate of mass transfer when the reaction rate and Schmidth number are increased.

Keywords: Heat and Mass transfer, chemically reactive MHD flow, Permeable surface.

MHD, magnetohydrodynamic; $Sc=\frac{\gamma }{D_m}$ , schmidt number; $\mathrm{Pr}=\frac{\gamma }{\alpha }$ , prandtl number; $Bi=\frac{h_f}{K}\sqrt{\frac{\gamma }{a}}$ , biot number; $M=\frac{\sigma B_0{}^2}{\rho a}$ , magnetic parameter; $G{r}_x=\frac{xg\beta \left(T_f-T_{\infty }\right)}{u_e^2}$ , local grashof number; $K=\frac{\gamma }{a}$ , reaction rate parameter; $\lambda =\frac{Q}{\rho a{C}_p}$ , internal heat generation parameter; $Ra=\frac{4{\sigma }^{*}{T}_{\infty }^3}{kK\prime }$ , radiation parameter; $Br=\frac{\mu u_e^2}{k\left(T_f-T_{\infty }\right)}$ , brinkman number; $F_w= \pm \frac{2V_0}{\sqrt{a\gamma }}$ , suction/injection.

The hydromagnetic flow and heat transfer over a surface have practical, industrial and engineering applications in the streamlined expulsion of plastic sheets, paper creation, glass blowing, metal turning, drawing plastic film, aerodynamic expulsion of plastic sheets, condensation process of metallic plate in the cooling bath and expulsion of a polymer sheet from a colour. Ali J Chamkha¹ solved general boundary layers governing steady, Laminar, hydromagnetic flow with heat and mass transfer over a permeable cylinder moving with a linear velocity in the presence of heat/absorption, chemical reaction, suction/injection effects and uniform transverse magnetic field using standard, fully implicit, iterative, tri-diagonal finite difference method.Aziz A² obtained a similarity solution for a Laminar boundary layer flow over a flat plate with a convective surface boundary condition. Bhattacharyya & Gorla³ solved the axisymmetric boundary layer flow and heat transfer past a permeable shrinking cylinder subject to surface mass transfer using finite difference method of quasilimearization technique. Bhattacharyya & Layek⁴analyzed the distribution of a reactant solute undergoing first order chemical reaction in the boundary layer flow of an electrically conducting incompressible fluid over a permeable stretching sheet subjected to suction or blowing using finite difference method of quasilinearization technique. Also,Bhattacharyya k,⁵ considered the effects of heat source /sink on the steady two dimensional MHD boundary layer flow and heat transfer past shrinking sheet with wall mass suction using finite difference method of quasilinearization technique. Emmanuel, Maurice Arthur et al.⁶ investigated the hydromagnetic flow over a flat surface with convective boundary condition and internal heat generation in the presence of chemical reaction using Newton-Raphson Shooting method along with fourth order Runge-Kutta algorithm. Gnaneswara & Sandeep⁷ analyzed the heat and mass transfer in Carreau fluid flow over a permeable stretching sheet with convective slip condition in the presence of applied magnetic field, nonlinear thermal radiation, cross diffusion and suction/injection effects using Runge-Kutta and Newton’s method. Also, Nayak⁸ considered a steady MHD flow of a viscous conducting fluid past a stretched permeable vertical permeable surface with heat generation/Absorption, thermal radiation and chemical reaction using Runge-Kutta method based on Shooting technique. Prakash et al.⁹ 10.0pt;" examined the hydromagnetic two dimensional boundary layer flow of a non-Newtonian fluid accompanied by heat and mass transfer towards an exponentially stretching sheet in the presence of chemical reaction and thermal radiation using casson model. Sulochana & Kishor Kumar¹⁰ used shooting technique to analyze the heat and mass transfer in magnetohydrodynamic flow over a stretching sheet in the presence of thermal radiation and chemical reaction. Seth et al.¹¹ used exact solution in closed form and numerical solution to investigate an unsteady hydrodynamic natural convection flow with heat and mass transfer of a viscous incompressible, electrically conducting, chemically reactive and optically thin radiating fluid past an exponentially accelerated moving vertical plate with arbitrary ramped temperature, embedded in a fluid saturated in a porous medium. Also, Hayatet al.¹² obtained convergent series solutions for a boundary layer flow of a Nano fluid over power-law stretched surface in the presence of applied magnetic field and chemical reaction with heat and mass convective conditions. Ishak¹³ provided a similarity solution for a steady, Laminar, boundary layer flow and heat transfer over a permeable flat plate in a uniform free stream with the surface of the plate heated by convection from a hot fluid. Also, Makinde & Olanrewaju¹⁴ analyzed the effects of thermal buoyancy on the laminar boundary layer about a vertical plate in a uniform stream of fluid under a convective surface boundary condition using fourth order Runge-Kutta iteration scheme. Olanrewaju et al.¹⁵used Shooting iteration technique with sixth order Runge-Kutta integration scheme to analyze the effects of internal heat generation, thermal radiation and buoyancy force on the Laminar boundary layer flow about a vertical plate in a uniform stream of fluid under a convective surface boundary condition. 

This work extends the work of Aziz,² Emmanuel et al.,⁶Ishak,¹³ Makinde & Olanrewaju¹⁴ and Olanrewaju et al.¹⁵ to include buoyancy force and fluid injection or suction on heat and mass transfer over a permeable surface of a chemically reactive Magnetohydrodynamic fluid flow in the presence of heat source and sink and thermal radiation.

Consider a steady, two dimensional Laminar flow of a viscous incompressible and electrically conducting fluid, coupled with heat and mass transfer past a permeable stretching surface. The permeable surface is to give way to possible wall fluid suction/injection. A stream of cold fluid at temperature $T_{\infty }$  is moving over the right side of the surface with a uniform velocity $U_{\infty }$ .while the left surface is heated by convection from a hot fluid at temperature$T_f$ which provides a heat transfer coefficient$h_f$ . Normal magnetic field of constant strength is applied externally along the surface and the density variation due to buoyancy effects is taken into account in the momentum equation. Figure 1

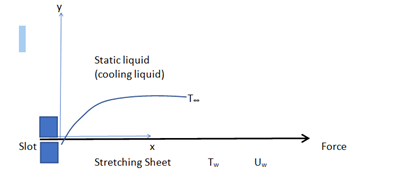
Figure 1Flow configuration and coordinate system.

The governing continuity, momentum, energy and concentration equations are:

$\frac{\partial u}{\partial x}+\frac{\partial \text{v}}{\partial y}=0$  (1)

$u\frac{\partial u}{\partial x}+\text{v}\frac{\partial u}{\partial y}=\gamma \frac{{\partial }^{2}u}{\partial y^2}+g\beta \left(T-T_{\infty }\right)-\frac{\sigma B_0^2\left(u_e-u\right)}{\rho }$ (2)

$u\frac{\partial T}{\partial x}+\text{v}\frac{\partial T}{\partial y}=\frac{K}{\rho C_p}\frac{{\partial }^{2}T}{\partial y^2}+\frac{\gamma }{C_p}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{\sigma B_0^2{(u_e-u)}^2}{\rho C_p}+\frac{Q}{\rho C_p}\left(T-T_{\infty }\right)-\frac{1}{C_p}\frac{\partial q_r}{\partial y}$  (3)

$u\frac{\partial C}{\partial x}+\text{v}\frac{\partial C}{\partial y}=D_m\frac{{\partial }^{2}C}{\partial y^2}-K_r{(C-C_{\infty })}^n$ (4)

$u\left(x,0\right)=0, \text{v}\left(x,0\right)=\pm V_0 ,-k\frac{\partial T}{\partial y}\left(x,0\right) = h_f\left(T_f-T\left(x,0\right)\right), C\left(x,0\right)=C_f$  (5)

$u\left(x,\infty \right)=u_e=ax, T\left(x,\infty \right)=T_{\infty },C\left(x,\infty \right)=C_{\infty }$ (6)

$T^4\approx 4T_{\infty }^{3}T- 3T_{\infty }^4$ (8)

$q_r=-\frac{16T_{\infty }^3{\sigma }^{*}{}^{}}{3K}$ $\frac{{\partial }^2{T}^4}{\partial y^2}$ (9)

$\eta =x^{\frac{1}{2}}y\sqrt{\frac{u_e}{\gamma }} , u=u_{e}f\prime , v=\frac{1}{2}\sqrt{\frac{u_e}{x}\gamma }\left(\eta f^{\prime }-f\right), \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }}, c\left(\eta \right)=\frac{C-C_{\infty }}{C_f-C_{\infty }}$ (10)

$u=\frac{\partial \psi }{\partial y} and v=-\frac{\partial \psi }{\partial x}$ (11)

$f\prime \prime \prime +\frac{1}{2}ff″+G{r}_x\theta +(M_x+D{a}_x)(1-f\prime )=0$ (12)

$\left(1+\frac{4}{3}Ra\right)\theta ″+Br{\left(f″\right)}^2+Br{M}_x{\left(1-f\prime \right)}^2+\frac{1}{2}Prf\theta \prime +Pr{\lambda }_x\theta =0$ (13)

$\varphi ″+\frac{1}{2}\text{Sc}f\varphi \prime -Sc{B}_x{\varphi }^n=0$ (14)

$f\prime \left(0\right)=0 , f\left(0\right)= F_{wx} , - \theta \prime \left(0\right)=Bi\left( 1 - \theta \left(0\right)\right),\varphi \left(0\right)=1$  (15)

$f\prime \left(\infty \right)=1,\theta \left(\infty \right)=0,\varphi \left(\infty \right)=0$  (16)

where the prime symbol represents the derivative with respect to $\eta$ For the momentum, energy and concentration equations to have similarity solutions, the parameters Grx, Bx, Mx, Dx, ${\lambda }_x$ must be made constants.

Numerical procedure

The governing equations and the boundary conditions are solved using Runge-Kutta method based on sixth order Shooting technique.

Particular cases

1. For a chemical reaction of first order when n=1 and in the absence of buoyancy force and heat source/sink i.e when$Gr=\lambda = F_w=0$ , then the results of this paper is the same as Emmanuel et al.⁶
2. For a fluid which is not chemically reactive in the absence of the magnetic field, i.e when, Sc=K=M=Br=Fw=0 then the result of this paper will be same as Olanrewaju et al.¹⁴
3. In the absence of heat source/sink, buoyancy force, radiation effects and magnetic field for a non-chemically reactive fluid i.e when $\lambda =Gr=Ra=M= F_w=Sc=K=Br=0$ , then the result of this paper will be same as Makinde & Olanrewaju,¹⁴ Aziz² and Ishak.¹³

Numerical calculations have been carried out for different values of thermo physical parameters controlling the fluid dynamics in the flow region. Table 1 shows the comparison of Emmanuel Maurice Arthur et al.⁶ with the present work for the numerical values of skin friction coefficient, local Nusselt number  together with Sherwood number and there was a perfect agreement of result in the absence local Grash of number Gr, internal heat generation  and injection/suction F_w i.e for. Table 2 shows the comparison of Olanrewaju et al.¹⁴ with the present work for the numerical values of skin friction coefficient, local Nusselt number together with plate surface temperature and there was a perfect agreement of result when Sc=K=M=Br=F_w=0 Table 3 shows the comparison of the present work with the work of Makinde and Olanrewaju,¹⁴ Aziz² and Ishak¹³ for numerical values of  and and there was a perfect agreement of result when and Pr=0.72.

Figures 2-17, together with Tables 4-6shows the computational results showing the effects of various thermo physical parameters on the electrically conducting and n-th order homogeneous reacting fluid velocity, temperature, concentration as well as skin-friction coefficient, plate temperature, rate of heat and mass transfer over the vertical plate. It is clear from Table 6 that with more injection of the chemically reactive and electrically conducting fluid into the flow system, then there was a corresponding rise in the skin-friction coefficient. The same result was observed by increasing the values of the Magnetic parameter, Brinkman and Grashof numbers. In Table 5, the varying values of the reaction rate parameter increased the rate of mass transfer within the flow system. On the other hand, when the order of the chemical reaction was increased, there was a retardation of the rate of mass transfer. Table 6 shows the computation of the values of plate temperature and the Nusselt number for various values of the thermo physical parameters for a first order chemical reaction with variations in Ra, M, Bi, Pr,and Br. Some of the parameters like Ra, Bi,, M and Br increased the plate temperature while F_w and Pr decrease in the plate temperature. The rate at which heat is transferred, increased by increasing the values of the Prandtl and Biot numbers as a result of convective heat exchange at the plate surface. There was a retarding effect on the heat transfer rate as Br, Ra and were increased due to viscous dissipation. The Lorentz force due to the magnetic parameter was seen to be distractive to the rate of heat transfer.

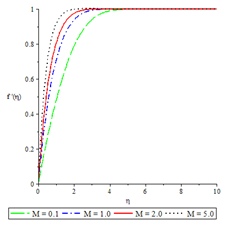
Figure 2Velocity profiles for , ,

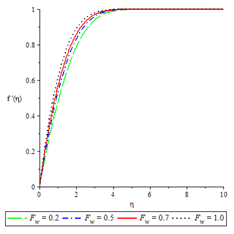
Figure 3Velocity profiles for , ,

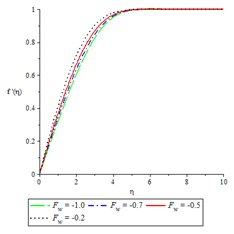
Figure 4velocity profiles for , ,

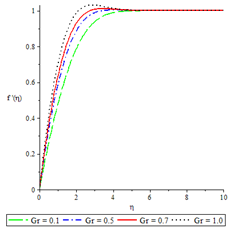
Figure 5Velocity profiles for , ,

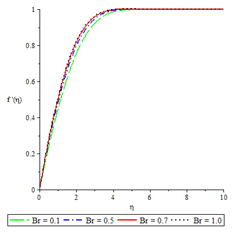
Figure 6Velocity profiles for , ,

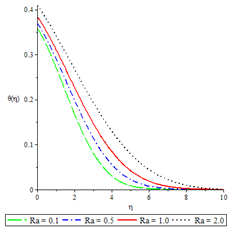
Figure 7Temperature profiles , ,

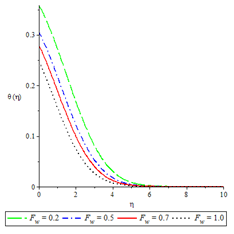
Figure 8Temperature profiles for ,

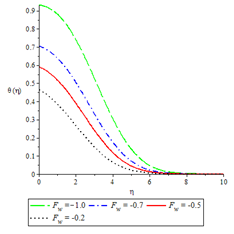
Figure 9Temperature profiles for ,

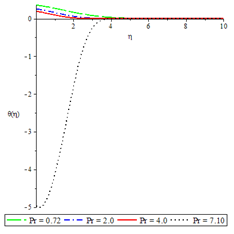
Figure 10Temperature profiles for ,

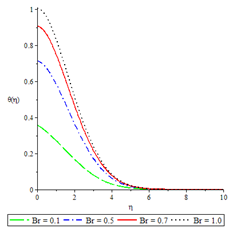
Figure 11Temperature profiles for ,

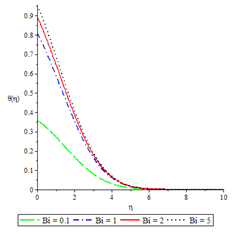
Figure 12Temperature profiles for ,

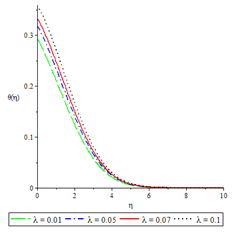
Figure 13Temperature profiles for ,

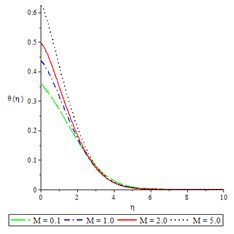
Figure 14Temperature profiles for ,

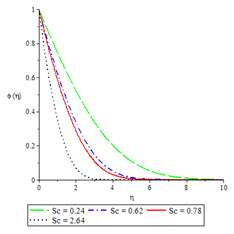
Figure 15Concentration profiles for ,

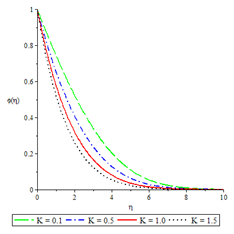
Figure 16Concentration profiles for ,

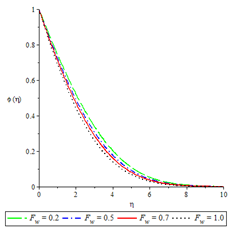
Figure 17Concentration profiles for ,

Velocity profiles

Figures 2 to 6 show the influence of some of the controlling parameters on the velocity boundary layer. The fluid velocity was lower at the plate surface and increased to the free stream value satisfying the far field boundary condition. In Figure 2, the distractive force due to Lorentz force increased as the magnetic parameter increased because there was a very consistent drop in the longitudinal velocity and therefore the momentum boundary layer thickness get thinner. An increase in fluid injection, Grashof number and Brinkman number have the same effects on both the momentum boundary layer and velocity with the Magnetic parameter as shown in Figures 3 to 6.

Temperature profiles

The effects of various controlling parameters on the temperature distribution are shown in Figures 7-14. It is noteworthy that, the temperature reaches its maximum at the permeable plate surface and asymptotically decreases to a minimum zero value far away from the plate, thereby satisfying the boundary condition. Also, increasing the magnetic parameter increases the fluid temperature which in turn, increases the thermal boundary layer. This is attributed to the effect of Ohmic heating on the flow system. An increase in the Biot number gave rise to increase in fluid temperature due to the convective heat exchange between the hot fluid at the lower surface of the plate and the cold fluid at the upper surface of the plate and so there was also a thickening of the thermal boundary layer. The same reason can be given for the Brinkman number, internal heat generation parameter and radiation parameter but an opposite trend was observed by increasing the Prandtl number and fluid injection and so the rate of thermal diffusion was lowered within the boundary layer and a thinning of the thermal boundary layer was also observed.

Concentration profiles

The effects of the controlling parameters on concentration profile were shown in Figures 15-17. The boundary conditions were fulfilled as the graphs indicate maximum concentration at the permeable plate surface and an asymptotical decrease to the prescribed free stream value. Fluid injection and suction, Schmidt number and the reaction rate parameters decreased the rate of mass diffusivity. The solutal boundary layer also decreased for all the three controlling parameters.

This work examined the analysis of a steady, two-dimensional, chemically reactive MHD flow of heat and mass transfer of a viscous incompressible chemically reactive and electrically conducting fluid over a permeable surface. The similarity equations were obtained and solved numerically using Runge-Kutta method based on Shooting technique. Numerical results were presented, illustrated and analyzed graphically with all the controlling thermo physical parameters in the velocity, temperature and concentration profiles. Conclusively, it was noted that:

We appreciate the comments of the reviewers in improving the quality of the paper.

The authors have declared that no competing interest exists.

1. Ali J Chamkha. Heat and Mass transfer from MHD flow over a moving permeable cylinder with heat generation or Absorption and chemical reaction. Communications in Numerical analysis. 2011.
2. Azia A. Similarity solution for Laminar boundary layer over a flat plate with a convective surface boundary condition. Communication of Nonlinear Science and Numerical simulation. 2009;14(4):1064‒1068.
3. Bhattacharyya K, Gorla RSR. Boundary layer flow and heat transfer over a permeable shrinking cylinder with surface mass transfer. International Journal of Applied Mehanics and Engineering. 2013;18(4):1003‒101 2.
4. Bhattacharyya K, Layek GC. Chemically reactive solute distribution in MHD boundary layer flow over a permeable stretching sheet with suction or blowing. Chemical Engineering Communications. 2010;197:1527‒1540.
5. Bhattacharyya K. Effects of heat source/sink on MHD flow and heat transfer over a shrinking sheet with mass suction. Chemical Engineering Research Bulletin. 2011; 15(1):12‒17.
6. Emmanuel Maurine Arthur, Ibrahim Yakubu Seini, Azizu Seidu. On chemically reacting Hydromagnetic flow over a flat surface in the presence of radiation with viscous dissipation and convective boundary condition. America journal of Applied Mathematics. 2014;2(5):179‒185.
7. Gnaneswara Reddy Machireddy, Sandeep Naramgari. Heat and Mass transfer in radiative MHD Carreau fluid with cross diffusion. Ain Shams Engineering Journal. 2016.
8. Nayak MK. Steady MHD flow and heat transfer on a stretching vertical permeable surface in the presence of heat generation/Absorption, thermal radiation and chemical reaction. AMSE Journals. 2016;85:91‒104.
9. Prakash J, Durga Prasad P,Vinod Kumar G. et al. Heat and Mass transfer Hydromagnetic radiative casson fluid over an exponentially stretching sheet with source/sink. International Journal of Engineering Science Invension. 2016;5(7):12‒23.
10. Sulocchana C, Kishor Kumar MK. Numerical investigation of heat and mass transfer in radiative Magnetohydrodynamic flow with chemical reaction. International Journal of Advanced Science and Technology. 2016;97:25‒36.
11. Seth GS, Sharma R, Kumbhakar B. Heat and Nass effects on steady MHD Natural convection flow of a chemically reactive and radiating fluid through a porous medium past a moving vertical plate with arbitrary Ramped temperature. Journal of Applied fluid Mechanics. 2016;9(1):103‒117.
12. Tasawar Hayat, Madiha Rashid, Maria Imtiaz, et al. Magnetohydrodynamic stretched flow of a nanofluid with power-law velocity and chemical reaction. AIP Advances. 2015;5(11):117‒121.
13. Ishak A. Similarity solution for flow and heat transfer over a permeable surface with convective boundary conditions. Applied Mathematics and computation. 2010;217(2):837‒842.
14. Makinde OD, Olanrewaju PO. Buoyancy effecta of thermal boundary layer over a vertical plate with convective surface boundary condition. Journal of fluid Engineering. 2010;132(4):044502.
15. Olanrewaju PO,Gbadeyan JA, Hayat JA, et al. Effects of heat generation, thermal radiation and buoyancy force on a boundary layer flow over a vertical plate with convective surface boundary condition. South Africa Journal of Science. 2011;107:9‒10.
16. Conte SD, Boor C. Elementary Numerical Analysis. New York: McGraw-Hill Book Co; 1981.
17. Jain MK. Numerical Solution of Differential Equations. India: Wiley Eastern Ltd:  1984.
18. Jain MK, Iyengar SR, Jain RK. Numerical Methods for Scientific and Engineering Computations.India: Wiley Eastern Limited:  1985.
19. Krishnamurthy EV, Sen SK. Numerical Algorithms. India: Affiliated East-West Press Pvt. Ltd; 1986.
20. Heck A. Introduction to Maple. 3rd Ed, Springer-Verlag; 2003.