It is interesting to note that pseudo-hermiticity condition fails to preserve spectral invariant nature in nearly degenerate quantum states of single and double well operators. In other words no spectral similarity exists between nearly degenerate energy eigenvalues of Hermitian operator and corresponding PT-symmetry operator.

Keywords: anti–PT–symmetry, pseudo-hermiticity condition, spectral variance, hermitian operator, nearly degenerate eigenvalues

Quantum postulates are based on self-adjoint operators satisfying the condition

$H=H^{†}$(1)

In terms of energy eigenvalues $E_n$ and corresponding eigenfunction one can write the above relation as¹

$H={\displaystyle \sum _n{E}_n}\left|{\psi }_n><{\psi }_n\right|$ (2)

The above relation assumes the well behaved nature of wave function

$|{\psi }_n>={\psi }_n\to 0(x\to \pm \infty )$ (3)

As far as the author knows, almost all Hermitian operators satisfy this condition. Suppose the wave functions and corresponding operator can be transformed as

$<{\psi }_n\left|H\right|{\psi }_n>=<{\varphi }_n\left|h\right|{\varphi }_n>$(4)

then it is implied that $|{\varphi }_n>=S^{-1}|{\psi }_n>$        (5), $<{\varphi }_n|=<{\psi }_n|S$  (6), $h=S^{-1}HS$       (7)

Now question arises as to if (i)h = hermitian or h = non–hermitian.² If h is hermitian then both $<{\varphi }_n|and|{\varphi }_n>$are well behaved like that of $|{\psi }_n>or<{\psi }_n|.$In other words spectral invariance exists between h and H. This may be a case of spectral invariance in non-degenerate quantum systems. In this context we would like to state that Mostafazadeh3 has explored some features relating to discrete non-degenerate levels. However till now no literature on similarity transformation is available involving nearly degenerate quantum levels pertaining to either single well or double well operators. In this context we would like to state that the recent paper of Rath4 has explored some interesting features on similarity transformation. However the aim of this paper is to explore eigenvalue relation between H and h, when H is having nearly degenerate eigenvalues.

Similarity Transformation operator(S)

Here we consider S as suggested earlier3 as

 $S=e^{-x^2/2}$(8)

Above operator satisfies the following relations

$S=S^{†}$ (9)

$PS{P}^{-1}=S$ (10)

$TS{T}^{-1}=S$ (11)

$PTS{(PT)}^{-1}=S$ (12)

In above P stands for space reflection $P\left(x\right)\to \left(-x\right);$T stands for time reversal operator $T\left(i\right)\to \left(-i\right).$² Further using this transformation one can see that the commutation relation remains invariant

$S^{-1}\left[x,p\right]S=\left[x,p+ix\right]=\left[x,p\right]=i$(13)

Or

$S\left[x,p\right]S^{-1}=\left[x,p-ix\right]=\left[x,p\right]=i$(14)

As reported earlier it is bounded³ in its behaviour.

Generation of space-time reversal model operators$h_{PT}^{(i)}$ 

As discussed earlier we can generate h as

$SH{S}^{-1}=h\to S^{-1}hS$ (15)

Now consider the following cases

$H=P^2-100x^2+x^4$ (16)

The above DWP (double well potential) was extensively studied in the past by many authors after the work of Balsa.5 However here we study the same after similarity transformation. The transformed operator is

$h_{PT}^{(1)}=p^2+i(xp+px)-101x^2+x^4$ (17)

Now consider another DWP as

$H=p^{(2)}-50x^2+x^6$ (18)

The transformed operator in this case is

$h_{PT}^{(2)}=p^2+i(xp+px)-51x^2+x^6$(19)

Let us consider another operator involving quartic and sextic term as

$H=p^2-10x^4+x^6$ (20)

The transformed operator in this case is

$h_{PT}^{(3)}=p^2+i(xp+px)-x^2-10x^4+x^6$ (21)

Let us consider model single well oscillator as

$H=p^2+x^2+\lambda \frac{\left|x\right|}{{(1+x^2)}^{2.5}}$ (22)

$h_{}^{(4)}=p^2+i{(xp+px)}^2+\lambda \frac{\left|x\right|}{{(1+x^2)}^{2.5}}$ (23)

Eigenvalues calculation

Here we solve the eigenvalue relation

$H|\Psi >=E|\Psi >$ (24)

With

$|\Psi >={\displaystyle \sum _m{A}_{m\pm k}}|m>$(25)

where$|m>$satisfies the condition $\left[p^2+x^2\right]|m>=(2m+1)|m>$ (26)

In this case one has to solve the recursion relation satisfied $A_m$ considering different matrix size [15] and calculate the eigenvalues.

In Table 1, we present convergent eigenvalues of the $H^{\left(i\right)}$ and in Figures 1,3,5,7 reflect the same. Further we also notice that nearly degenerate eigenvalues reflected in Table 1 also remain the same on exchange of $x\to p$ and $p\to x$ i.e

$H^{(1)}=x^2-100p^2+p^4$(27)

$H^{(2)}=x^2-50p^2+p^6$ (28)

$H^{(3)}=x^2-10p^4+p^6$ (29)

$H^{(4)}=x^2+p^2+\lambda \frac{\left|p\right|}{{(1+p^2)}^{2.5}}$ (30)

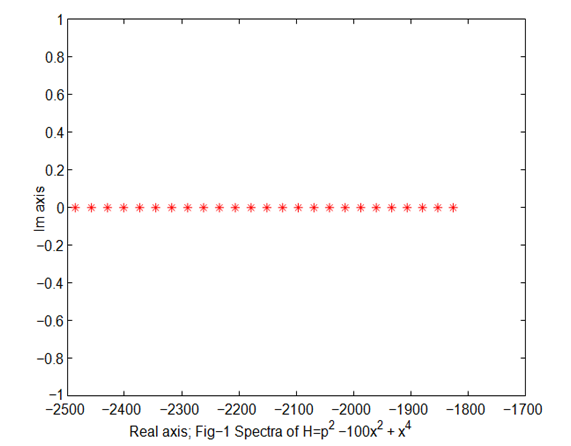
Figure 1 Nearly degenerate eigenvalues.

Figure 2 Spectral breakdown.

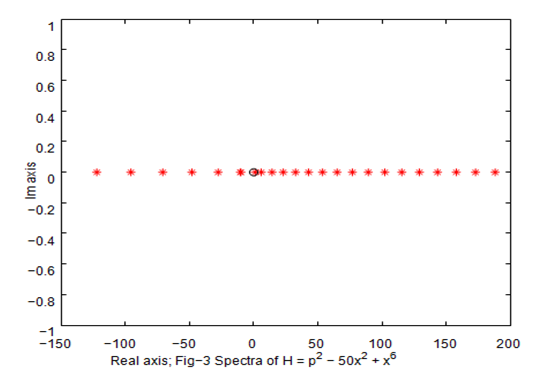
Figure 3 Nearly degenerate eigenvalues.

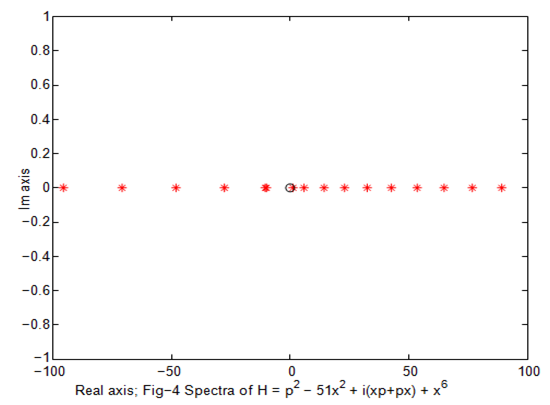
Figure 4 Spectral breakdown.

In the case of PT-symmetry operators we reflect spectral nature in Figures 2,4,6,8. The main conclusion of the paper is that the spectral invariance nature of Hamiltonian is violated on similarity transformation only in nearly degenerate eigenvalues i.e

$H\to E_n\ne {\in }_n\leftarrow h_P{}_T$ (31)

However if the parameter in question is small there is no spectral variance. For example consider the case of non-degenerate eigenvalues of

$H=p^2-x^2+x^4$(32)

And $h=p^2-2x^2+i(xp+px)+x^4$ (33)

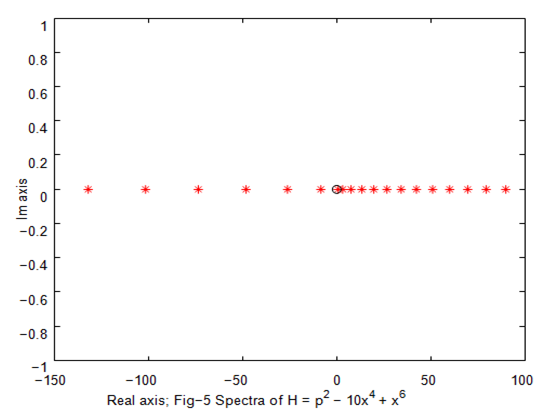
Figure 5 Nearly degenerate eigenvalues.

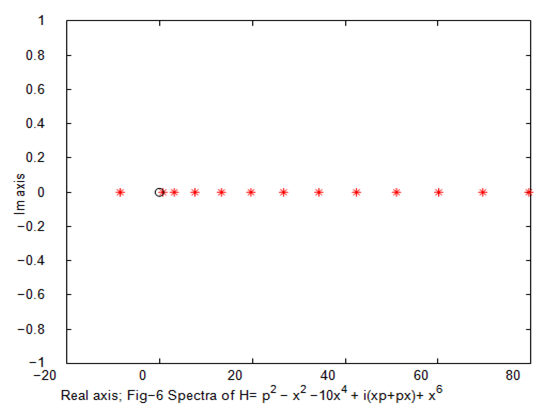
Figure 6 Spectral breakdown.

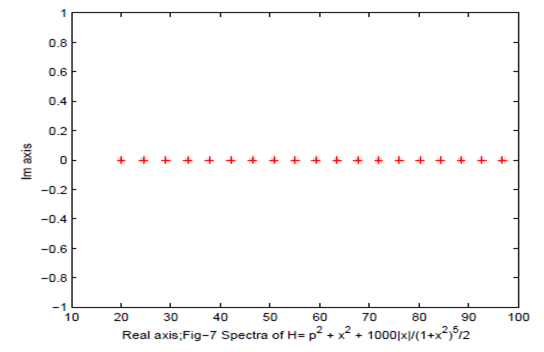
Figure 7 Nearly degenerate eigenvalues.

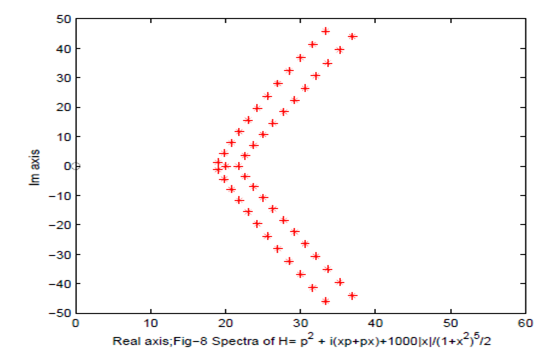
Figure 8 Spectral breakdown.

There is no spectral variance. Similar case exists for all operators cited above. However it is not known at present, why the spectral variance exists in large parameter reflecting nearly degenerate states?

Author is grateful to Referee for constructive remarks.

Authors declare that there is no conflicts of interest.

1. Bransden BH,  Joachain CJ. Quantum Mechanics. New Delhi: Pearson Education Ltd. 2000.
2. Bender CM, Boettecher S. Real spectra in Non-Hermitian Hamiltonians having PT-symmetry. Phys Rev Lett. 1998;80:5243−5245.
3. Mostafazadeh A. Pseudo-hermiticity versus PT-symmetry the necessary condition for the reality of the spectrum of a non-hermitian Hamiltonian. J Math Phys. 2002;43(1):205–214.
4. Rath B. Similarity transformation in PT-symmetry: limitations. Open Acc J Math Theo Phys. 2018;1(4):164–166.
5. Balsa R, Plo M, Esteve JG, et al. Simple procedure to compute accurate energy levels of a double-well anharmonic oscillator. Phys Rev. 1983;D28:1945–1948.