Statistical significance is the hallmark, the main thesis and the main argument to quantitatively verify or falsify scientific hypothesis in science. The correct use of statistic increases the reproducibility of the results and the is recently a widely wrong use of statistics and a reproducibility crisis in science. Today, most scientists can’t replicate the results of their peers and peer-review hinders them to reveal it. Next to an estimated 80% of general misconduct in the practices, above 90% of non-reproducible results and on top of this there is also a very high portion of generally false statistical assessment using statistical significance tests like the otherwise valuable t-test. The 5% confidence interval, a significance threshold of the t-test, is regularly and very frequently used without assuming the natural rate of false positives within the test system, referred to as the stochastic alpha or type I error. Due to the global need of a clear-cut clarification, this statistical research paper didactically shows for the scientific fields that are using the t-test, how to prevent the intrinsically occurring pitfalls of p-values and advises a random testing of alpha, beta, SPM and data characteristics to determine the right p-level and testing.

Keywords: t-test, p-value, biostatistics, statistics, significance, confidence, deviation, SPM, z score, alpha, type I, II, error

alpha error, type I error; beta error, type II error; t-test, Student’s t-test; σ, SD, standard deviation; p-value, t-test probability that the null hypothesis is false; type I error, false rejection of a true null hypothesis; type II error, non-rejected false null hypothesis SEM: standard error of the mean; SPM, Statistical process modeling; Z score, the standardized deviation of the random sample from the mean

Statistical significance is one of the key measures to verify scientific hypotheses. The t-test (Student, 1908, aka William Sealy Gosset) is one of the most suitable and most common ways to describe statistical significance in likelihood values, i.e. p-values, in empirical, social and natural scientific data.¹ It is used in all sciences and throughout the past and present literature to quantitatively verify of to falsify a hypothesis as a key part of the scientific method that comprises hypothesis formation, and subsequent verification and falsification to carve out the correct understanding of the world in science. Nevertheless, the level of type I errors (alpha errors) and type II (beta errors) is usually not defined. The reproducibility crisis in science is based on peer pressure, extreme job scarcity, bias, system-wide and systematically given false incentives, false data acquisition, lack of ALCOA, fake- quality publishing imperatives, and a false use of statistics and especially significance test.² This paper reviews why ‘statistical significance is often insignificant and illustrates the key importance of estimating the level of alpha and beta errors by example in the paired t-test statistics.³

Z scores were calculated according to the formula (1). PA represents the plate average, which was taken from all plates and experiments (N = all, n = all), hereafter referred to as global-PA, and from each individual plate with all of its experiments (N = 1, N = all).

$Z=\frac{x-PA}{\sigma }$ (1)

$\sigma =\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{(x_i-PA)}^2}}{N-1}}$ (2)

$t=\sqrt{n}\frac{PA-\mu }{\sigma }$(3)

$\frac{signal}{noise}=\frac{\widehat{x}-PA}{SEM(\widehat{x}-PA)}$ (4)

The standard deviation was calculated according to the standard formula given in (2), two-tailed, homoscedastic, with PA the plate average, n the sample size, µ the expected value of the null hypothesis, and $\sigma$ the standard deviation (2). The t-test was calculated using the paired excel function t-test that is widely used and which is derived from the standard t-test function (3) and its tables.

Randomization in the range 0-100 was performed for hundred experiments (N=100), or plates, with a test sample size of100 (n=100) to didactically illustrate the rate of false positives to be assumed in the scientific literature and experiments which are based on significant-testing using the student’s t- test. The overall sample size is yielded by the product of test samples (n=100) and plates (N=100), e.g. a sample size of 10.000 if all plates are considered, each plate is a replica of the 100 test samples. If we consider a statistical significance threshold of 5%, i.e. p<0.05, the experimenter must already assume a false positive rate of around 5%, i.e. also at the level p<0.05 using the paired t-test function. Figure 1A illustrates this using 34 randomization experiments of the above 100x100 Nxn plate matrix shown in Figure 1B (colors are coding for values; light green represents high and dark represents low). The results do not change if we use the z score of the global-plate-average or of single or local plates. The standard deviation indicates a range of roughly 2 to 7% of false positive assuming complete randomness of all date on all plates, i.e. N=100, n=100. This comparison between the plate average and of one plate row in hundred random replicas is regularly used in high-throughput screening (HTS), and the t-test is the most common measure of statistical significance that is believed to arise a p<0.05. This statistical experiment with random numbers illustrates that 5% of false positives can arise in t- test-based data evaluations, using the raw data, or normalized data like the z score for global and local PAs. The level of false positive can vary strikingly between completely randomized experiments (Figure 1A). Due to this statistical challenge, the question of the overall sample size arises and the question, how many replicas should be done to achieve a suitable confidence interval and statistical significance.

The number and rate of false positives diminish with the third plate (Figure 2C) (Figure 2D) but it will never level out but will remain even after 100 plates at the level of ca. 5%+/-2.5 (Figure 1A) and also after 1000 plates and more and also in general in most circumstances. The same effect can be seen for the normalized standard deviations of the z score using the global and local plate average (PA). Interestingly, the z score of the global PA always achieves an overall PA of exactly 0 and a $\sigma$of exactly 1, while the local plate averages will slightly vary depending on the experimental settings (e.g. $\sigma$=0.09 in the example with randomized values ranging from 0-100, N=100, n=100). Vice versa, the z score using the local PA will always achieve a local PA of exactly 0 and a local $\sigma$ of exactly 1, while the global plate average of all plates and test samples will deviate also depending on the experimental settings. Usually in an empirical experiment, the rate of false positives may be assumed as even higher, due to experimental burdens and obstacles, still, this result cannot tell which exactly the false positives are. Finally, the significance threshold level was further elucidated to see at which threshold of statistical significance the paired, homoscedastic, two-tailed t-test results in no or minimal false positives in the experiments with N=1000 replicate plates and n=100 test assays (Figure 2). As previously shown in (Figure 1A), the false positive rate is around 5% at a significance level of 5%, i.e. p<0,05. A significance level of 1% yields around 0.8% of false positives, p<0,005 results in 0,29% false positives, and p<0,001 yields only 0,04% false positives. After 24 randomizations, no false positive within n=100 of N=1000 replicas was only found for a t-test significance of p<0.0005, which is only seldom observed in science. The null hypothesis assumes that there is no difference between the plate test sample and the plate averages, or alternatively a suitable set of control sample, and the test sample, especially in screening. While the t-test reveals false positives at a confidence level of p<0,05, the z score derived confidence level does not show false positives in the testing if the averages of all plates are used, at a confidence interval of 95%. A z score of + or - 1.97 is 1.97 standard deviations away from the arithmetic mean and represents the 95% confidence interval or level. This confidence level was never exceeded by the random experiments and no single value did exceed this confidence interval in the random distribution SPM model that was used. The t-test-related false positives, the type I errors or alpha, usually showed a z score standard deviation $\sigma$ of 20-30% (N=100, n=100) which is a confidence interval of only 15–25%.

The combination of several statistics tools and adequate data and statistical process modeling (SPM) seem to be crucial to assure an ideal experimental system and subsequent analysis while taking all challenges of signal-to-noise, false-positives and false-negatives, decimals and artifacts into account. A random normal distribution yields similar results and can be done to be more precise in the model. The normal distribution similarly bears the alpha and beta errors just like in the randomized samples. As a consequence, the significance threshold level should be determined in advance and the p-value viewed in relation to a p-value of 0 expected false positives to obtain the scientific significances as s-value $\left(s=p_{error}-p\right)$ . Statistical significance gets a scientific meaning if related to zero type I and II errors, given as $s\left(I\right)=p(I_0)-p;s\left(II\right)=p(I{I}_0)-p.$  The negative value indicates the distance to a zero type I or type II error rate.

Although statistical significance is a key measure to quantitatively test hypothesis, the intrinsic rate of false positives, i.e. alpha or type I errors, in the statistical method is often underestimated, which can be found in the entire publication landscape and there is in fact not the need to mention a single paper. Especially the threshold value, or p-value or the confidence level, to be used in the statistical testing is often not determined to anticipate the intrinsic level of false positive in the experimental system. As a result, the statistical tests performed in the literature are not telling us how significant the result really is, as this can be only determined in relation to alpha, the naturally occurring type I error, or α error. Using random test samples, this paper shows that the rate of false positives clearly decreases as is still correctly assumed usually (Figure 1C) (Figure 1D), e.g. especially after 5, 10, and 20 plate replicate tests in this case, however, the rate of false positives, the $\alpha$ error, very much stabilizes subsequently at a level determined by the p-value, the threshold of statistical significance or confidence level (Figure 1A), and even after 1000 replications of the experiment (Figure 2A) when the correct p-value become apparent. Another result and conclusion for quantitative scientific t-test assays is the new stochastic requirement to estimate the right size of your test sample and the right amount of your replicas based on the experiment-specific relation of the p-value to $\alpha and\beta$, which can be done via randomized SPM testing in advance of the experimental planning. Every experimental and statistical system can be different and SPM models using randomization are advisable to adjust and find the right p-value and significance testing and overall conduct of the experiment and statistical tests. By the example, if you find 5% of positives and the rate of false positives is also 5% at a p-value of p<0.05, it would be hard to believe that these are correct positives. The difference between the type I error alpha and the positives found in your test system is a crucial indicator for your significance tests. The rate of truly positives $r_{true}$ equals the rate of significantly positives,$r_{p-value}$, minus the rate of $\alpha$ errors minus the rate of residual experimental errors, as is summarized in equation 5 and 6. Hence, the p-value threshold level can immediately be adjusted or corrected by the alpha level (equation 6) to set up an ideal statistical test.

$r_{true}=r_{p-value}-\alpha -\epsilon$(5)

$r_{true}=r_{p-value(alpha)}-\epsilon$ (6)

The t-test bears still much utility and can be widely used, also if one has to assume that false positives will be inherent. In some cases, it will not be easy to achieve an ideal signal-to-noise ratio and it will not be possible to use a confidence interval or p-value that assures no false positives. In fact, a significance of p<0.0005 that would be required in a random noise scenario is often hard to achieve, as shown in Figure 2A. In a normal distribution of the gauss-shape the testing becomes easier if the two populations are separated sharply from each other but the type I and II error should be known. In a perfectly normalized dataset in which a minimal difference is to be tested SPM is highly advisable and random numbers can be used to model the noise in any standardized dynamic range, and if needed also in the form of a normal distribution, which will yield a different type I and II error rate and level.

Generally, the better the SPM model the better the result. In the many cases in which it will not be possible to assure no false-positives, it is advisable to know and to keep the difference in mind (5,6). Another important although more trivial point that is sometimes forgotten is to consider is the right amount of decimals in small-change population statistics. A didactical model of using the false amount of decimal numbers for statistical testing, e.g. the t-test significance tests, is provided in Figure 2B. Although the same test sample is used, a high-order significance was estimated by the t-test due to the wrong amount of decimals, which is a frequent mistake in science and in automated and AI driven data analysis in general. The unmeasurable decimal places can be an artifact of the instrument, the day, the normalization, the equilibration, the routine, basically of any uncontrollable and unnecessary detail, which are remainders that have nothing to do with the experimental hypothesis and question. Nevertheless, such minimal trends can also cause a very strong bias in t-test significances (Figure 2B).

In summary, it seems to be helpful and important to perform dry run statistical tests using randomized data for all mean comparison test like the t-test, to optimize the statistical methods and procedures in advance of the experiments and to know the intrinsic rate of false positives, samples, and test runs needed. In analogy, an additional testing can be performed to estimate the number of false negatives, and to know which signal-to-noise-ratio would be required that would be ideal. A dry run can be helpful for planning and for the SPM statistical models and to learn about the distribution type, the assays, instruments, dynamic range, signal-to-noise ratio, the quantity of reliable decimals that can be tested in advance, sensitivity, reliability, and much more. Estimates about the variance will also help to decide which t-test is to be used. For instance, the mean comparison test should be only used to identify if the null hypothesis, which states that both random samples belong to the same population, is true or not. The unpaired t-test, aka Welch test, should be used if the variance will or will have been different between the two populations. More than two populations cannot be measured simultaneously, and the paired t-test is intended to be used for two populations that depend on each other, e.g. cross-over and before- and after-treatment groups, repeated measurements, or correlated and functional groups.

False positives are referred to as type I error and false negatives are termed as type II errors. While the paired t-test used in correlated or dependent groups will yield a constant amount of false positives, it might be helpful to use the unpaired t-test in positively correlated groups and the paired t-test in inversely correlated groups. This way, the type I error might diminish at the cost of the overall p-value standardization, i.e. the same amount of type I errors independent of the dependency type and level. Type II errors, i.e. false negatives, are indicated by the power of the t-test, which can be also tested in mathematical models in advance. Didactically, one can keep in mind,4 that the paired t- test is better for the power of positively correlated groups at the cost of more type I errors, and the unpaired is more stable. Ideally, screening and test systems should and can be optimized in advance to achieve minimal type I and II errors, while keeping a high sensitivity, dynamic range, signal-to-noise and power of the t-test. Many new statistical ways are thinkable to better standardize, acquire and process the data to achieve these goals. SPM and statistical assays like the t-test are still leading the stochastic way, as they are easier, better understood and better to interpret, transparent and more standardized. Still, the type I and type II errors should not be regularly omitted in the statistical analysis of science of today. Indeed, in clear cases they might not be needed while in others they are crucial.

Generally, the null hypothesis should be chosen in a way that the more disagreeable consequences of a potentially wrong decision will appear as a type I statistical error.⁵ The higher the risk of a potential false decision, e.g. an approval of an entity for human use, the smaller should be the likelihood to make a type I error.⁵ A paired t-test with a significance threshold of p<0.05 (5%) has yielded around 5% type I errors in equal random data sets, which can represent data noise or only one population. Thus, this work suggests the importance of the relationship of p-value and alpha error, and the difference can be used as statistical indicator of the significance of the t-test significance.

The t-test derived p-value does not directly specify the alpha error, i.e. the level of type I errors. Due to this is always required to separately check for the probability of alpha and beta, type I and type II, errors and power, as indicated by formula 7 and 8 and to use an SPM data model.⁵

$statisticalconfidence=S_{\alpha }:=1-\alpha$ (7)

$power=S_{\beta }:=1-\beta$      (8)

Moreover, the central statistical theorem or main theory of probability (German: Hauptsatz der Mathematischen Statistik, English: The Main Statement of Mathematical Statistics), also known as the Glivenko-Cantelli theorem,5 states that the empirical distribution function of the sample asymptotically converges with the actual distribution function by expanding the random sample. With regard to the t-test example discussed in this work (N=1000, n=100; Figure 1C & 1D, Figure 2) it becomes clear that the overall rate of natural type I errors, i.e. alpha errors, can remain constant over thousands of experimental replications and more. Tiny differences can cause huge significances (Figure 2B), and this is also the case if there is no change in the population observable and in random testing too. The t-test can only test if the null hypothesis is true or not by comparing the arithmetic means and $\sigma$ of the groups. Small difference also come in play if the two sample populations are indeed only one, and the SPM and random data noise can indicate the rate of false positives in a one population sample to normalize and to standardize the t-teat p-value, i.e. the real significance of the significance (equation 5 and 6). Type I and type II errors stem from the confidence and power of the test (equation 7 and 8). Hence, this humble work advises to include a statistical pre-assessment and SPM before the conduct of the experiment and a statistical analysis to identify the right p-value, to assure a higher level of statistical confidence and power, $S\left(\alpha \right)andS\left(\beta \right)$(equation 7+8) respectively, and to better plan the conduct of the experiment, the ideal sample size, and the statistical analysis, in advance, as is usually done in biomedical and most clinical studies, for example, by including α and β rates, when it is helpful.

Figure 1 Representation and illustration of type I or alpha errors in t-test statistics. (A) Falsely significant positives arise at the level of the significance threshold, i.e. p<0.05, of the t-test. In 100 experiments with 100 test-assays, a rate of 5% false-positive type I error was found in random testing at a significance threshold of 5% (p<0.05). A p-value of 0,05 does not represent α the type I error in general and only in this case for p<0.05 when 5% false positives are to be expected. Accordingly, the alpha and beta error should be always estimated in advance to adjust the right p-level and sample size.

Figure 2 The p-value threshold of statistical significance on the false positive rate. (A) The p-value confidence level is given as a percentage of the respective test samples (N=1000, n=100) in 24 randomizations of all experiments (N=1000, n=100). Note that a level of p<0.05 is results in 5% of type I errors and only a p-value of p>0,0005 is significant enough to statistically assume no false positives in this experiment. As the p-value can vary, one must perform a randomized SPM to adjust the right level.

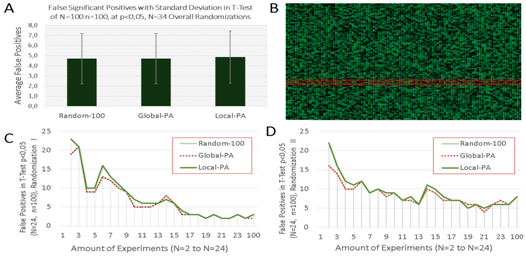
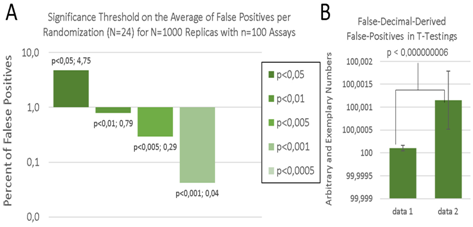
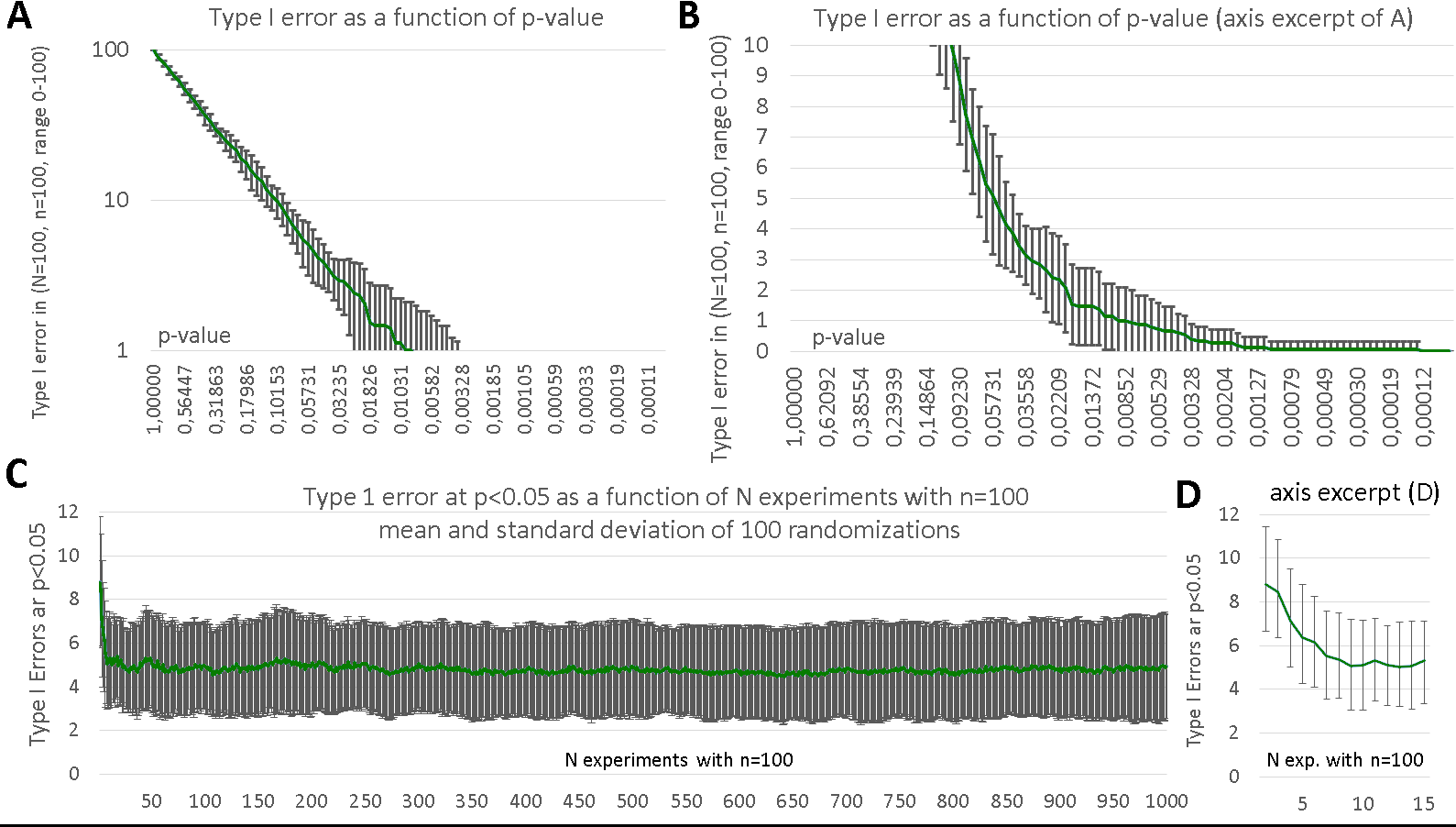
Figure 3 Type I errors as a function of p-value and sample size (number of experiments). (A) Type I errors as a function of p-value (B) excerpt of A. (C) Type I error as a function of sample size at a threshold level of p<0.05. (D) excerpt of C showing the mean with standard deviation of the observed type I error which is declining in only the very first 10 randomizations experiments (N with n=100) before it reaches a steady-state of false positives (N=10 experiments are enough to reduce random false positives of this range - as they would stay the same the next 990 additional experiments.) A t-test is instrumental in cases when the difference is not very clear-cut or obvious, and in this case type I errors usually also come into play making SPM a new scientific age necessity. The significance gets a scientific meaning when it is related to type I and II errors. Increasing sample size can not always improve the significances and type I errors but the right p-value threshold can. The p-value of no false positives S(I) [and optionally also negatives S(II)] serves as an indicator.

None.

Authors declare that there is no conflicts of interest.

1. Student. The Probable Error of the Mean. Biometrika.1908;6(1):1–25.
2. Baker M. 1500 Scientists lift the lid on reproducibility. Nature. 2016;533(7604):452–454.
3. Smith N. Why ’Statistical Significance’ is often Insignificant. Economics. Bloomberg Opinion. 2017.
4. Kohls Moritz. Zweistichproben-t-Test (2016). 2018.
5. Bartsch Hans Jochen. Paperback Mathematical Formulas. 18th edn. Germany: Fachbuchverlag Leipzig Carl Hanser Verlag; 1999.
6. Tucker Howard G. A Generalization of the Glivenko-Cantelli Theorem. Ann Math Statist. 1959;30(3):828–830.