In this brief paper, take a brief look at how Topology might apply to the Astrotheology Math. Much more work in this area remains to be done.
Keywords: topology, Alexander’s Knot, parametric equation, astrotheolgy
In this brief paper, we examine the Universal Parametric Equation as an Alexander Know. We see that the there is a topological invariant of “1” which of course, is equal to the Energy and time in Astrotheology (Figure 1).
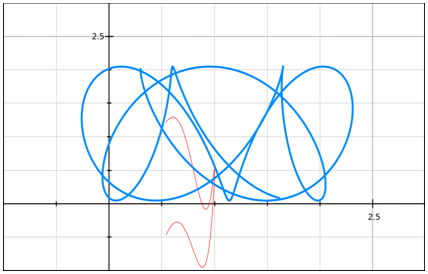
Figure 1 The universal parametric equation.
The Universal Parametric Equation:
Let
But R=2
So
Alexander’s polynomials
Reef or granny know
Let
In fact, all of Alexander’s Knots result in a the same answer =1, including the unknot.
The unknown is a circle. So the universal parametric equation is a knot.
Euler’s formula for polyhedra
For a circle Face
,
,
This is the
Triangle where
(Pythagoras)
We see that once again Occam’s razor applies this time to Topology and astrotheology.1-5
Author declares that there is no conflicts of interest.


