In this paper, we provide calculations on Astrotheology from Linear Algebra.1 Einstein was wrong about no absolute space and time and these calculations show how. Gravity, Mass, Density, and the zero vectors are used in calculations that show that the universe can be modelled as a tupple. We begin with gravity.
Product
Dot Product
Sum
Mass in the periodic table of the elements.
Cross Product
Let n=4
Dot Product /Cross Product
Roots 3, -2 = Eigenvalues.
Golden mean
Reduces to the bilinear form
Rotation matrix
Let
Figure 1
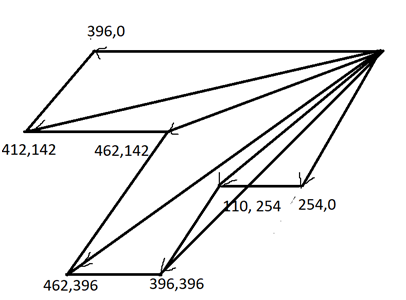
Figure 1 The universal vector space.
396,0
412,142
462,142
462,396
396,396
110,254
254,0
0,0
−−−−−
2492, 1330
Multiple be Operator Matrix
Multiple by
[Emin, Antigravity]
Subspace & the zero vector.
is Perpendicular to
This point lies on the y axis on the E-t golden mean parabola.
Perpendicular to
(-x,y,z) Perpendicular to (y,x,z)
(Likewise, for vectors in the III And IV Quadrant.
Multiple be Operator Matrix
Multiple by
Period T=251
Subspace on te zero vector.
is Perpendicular to
This point lies on the y axis on the E-t golden mean parabola.
(3,4,0) Perpendicular to (4,3,0)
(-x,y,z) Perpendicular to (y,x,z)
(Likewise, for vectors in the III and IV Quadrant.
Because you can’t have negative K.E., there is no such thing as negative time, so there is no orthogonal vector to the zero vectors (Figure 2).
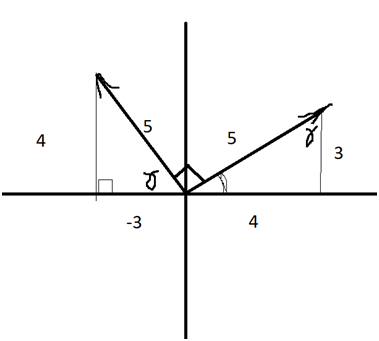
Figure 2 Orthogonal vectors.
Let
0=0 True!
Since time is K.E., and K.E is time, we measure K.E. relative to something - the zero vector. We also know that Mass is the dot product of E and t (Figure 3).

Figure 3 The zero vector.
And we know that Momentum, P, or
So
This disproves Einstein’s Relativity. There is a stationary point in the universe. It is the Zero Vector. Space and time are absolute.2
So this is how the universe crystallized into existence.3
But
Density
Equation of a plane
position vector
Mass Gap
r is orthogonal to n


