In recent years, significant amount of research has been done on the Evolutionary Algorithms (EA) to accurately estimate the parameters of the solar PV module. The equivalent electrical circuit model and the accuracy of the model parameters of the PV system are essential to understand the output characteristics, efficiency, and performance and to analyse the system with the variation of temperature and irradiation. This review article initially introduces the single diode, double diode and triple diode electrical equivalent circuit models of the PV and compares their advantages and disadvantages. Moreover this study will review the different EAs such as bio-inspired based, swarming based, chemistry/physics based and hybridization based algorithms to extract the model parameters of the PV system. Hybridized EAs provide better accuracy but exhibit slow convergence speed. Some EAs has the advantage of faster computational time and convergence speed compared to others. Much emphasis is given on the search range and control parameters setting of the algorithms since they ultimately control the performance of EAs.

Keywords: photovoltaic cell, single diode model, double diode model, three diode model, evolutionary algorithm, root mean square error

PV, photovoltaic; SDM, Single Diode Model; DDM, Double Diode Model; TDM, Three Diode Model; EA, Evolutionary Algorithm; RMSE, Root Mean Square Error; ANN, artificial neutral network; EA, evolutionary algorithm; MAE, mean absolute error; RAE, relative absolute error; MOOP, multi objective optimization problem; SSE, sum of squared error; GA, genetic algorithm; RGA, real coded genetic algorithm; IFSDE, improved free search differential evolution; PSO, particle swarm optimization; AFSA, artificial fish swarm algorithm; ABC, artificial bee colony; ABSO, artificial bee swarm optimization algorithm; HMCR, harmony memory considering rate; PAR, pitch adjustment rate; GGHS, grouping-based global harmony search; TLBO, teaching learning based optimization; GOTLBO, generalized oppositional teaching learning based algorithm

The rapid combustion of fossil fuels for energy generation could led to serious environmental issues such as accumulation of greenhouse gases in the atmosphere, acid rain, depletion of the ozone layers and climate change globally.¹⁻⁵ The solar photovoltaic (PV) has shown the great potential for the replacement fossil fuels to meet the energy demand in many countries globally especially in the area of distributed electric power generation.

The theoretical modeling and computer simulation of PV systems are essential to understand the output characteristics, efficiency and performance and to analyze the system with the variation of solar insolation, temperature.³⁻⁶ The Single diode (SD), double diode (DD) and triple diode (TD) equivalent circuit models have been discussed in many literatures to understand the non-linear current-voltage (I-V) and power-voltage (P-V) characteristics of the PV system. The most commonly used PV model is the SDM model due to simplicity and reasonable accuracy. However, at lower irradiance levels and varied temperatures, the accuracy of the SDM deteriorates closely to the open circuit voltage (V_OC).⁴⁻⁵ This model is represented by parameters of the generated photocurrent (I_PV) connected in parallel to the diode, saturation current flow through the diode (I_D), series resistance (R_S), shunt resistance (R_SH), and ideality factor (a).²⁻⁶ The addition of an extra diode to the SDM is known as the Double Diode Model (DDM) which is capable to improve the accuracy of the PV system and the extra diode accounts for the recombination current losses at the depletion region. The DDM is represented by seven parameters namely as; reverse saturation currents of two diodes (I₀₁ and I₀₂), diode ideality factors: diffusion (a₁) and recombination (a₂), I_PV, R_S, R_SH.^3,5,7 A third diode is added to the DDM known as TDM which represents the critical non-idealities of solar cells for the occurrence of leakage current at the grain boundary and surface of solar cells.⁷⁻⁸ The accurate estimation of the PV parameters using the model is required in order to simulate the behaviour and evaluate the performance of the PV system both standard test conditions (STC) and real measured conditions with the variation of temperature and irradiation.³⁻⁸ Estimating PV parameters can cause decisions to be made wrongly in terms of sizing of the power converters and instability in controllers.¹⁰

The modelling parameters of the PV could be extracted from datasheet information given by PV manufacturers at STC and from the measured data.⁷ However, the conventional methods for estimating parameters of all solar cell is classified as Analytical method and Numerical method.¹¹ When using the analytical method, several key points information’s of the I-V curve is required such as open circuit voltage (V_oc), short-circuit current (I­_sc), voltage and current values at maximum Power Point (MPP), and the axial intersection slopes of the I-V curve.¹³ This method offers simple and faster computation of the PV parameters.² The accuracy of this method relies mainly on the chosen points on the I-V curve, wrongfully selection of these points can give the result with significant errors.¹³ The numerical method is based upon the simulated I-V curve fitting onto the experimental curve using iterative algorithm. This method is computationally expensive since the process of fitting all points on the I-V curve is relatively large.¹³⁻¹⁴ The accuracy of this method depends on the value of the initial extracted parameters, cost function and fitting algorithm. The limitations of the conventional parameter extraction method are the loss of its ability to give accurate output values when the model parameters increase.^13,15 The detailed discussion of the analytical and the numerical methods can be found in references.^{3,11,14,16,17} The Artificial Neutral Network (ANN) is a method to estimate the PV parameters using only temperature and insolation readings. Accuracy of this method deteriorates when other environmental conditions such as shading occurs.¹⁸ A recent research suggests that the Evolutionary Algorithm (EA) approach would give better accuracy and reliability to estimate the PV parameters .¹⁷⁻²⁴ The drawbacks of adopting analytical and numerical methods can be resolved using the stochasticity nature of EA which estimates optimal PV parameter values by minimizing the predefined objective function.^12,15 The nomenclature review of EA was presented in literature,¹⁶ where the authors outlined the different types of EA. Furthermore, litereature³ reviewed the objective functions, types of electrical models, search ranges of parameters and types of data used for EAs and their hybrid forms. This paper presents more objective function such as search ranges, the different settings of EAs control parameters, the statistical analysis of the PV (which is not given in References 3,17). This paper also highlights the various improvements and contributions by different technical literature for the SDM, DDM and TDM.

It is essential to develop a mathematical model that represents accurately the I–V and P-V behaviour of the PV module.¹³ Several electrical equivalent circuit models of the PV have been discussed in literatures to understand the non-linear I-V and P-V characteristics but in practice the more commonly used models are the SDM and DDM.¹⁵

Single diode model (SDM)

The equivalent circuit of a PV cell consists of a current source in parallel with a single diode and two resistances: shunt and series resistance as shown in Figure 1.

Figure 1 Single diode equivalent circuit model of the PV.

The SDM model is capable to define the entire I-V and P-V curve of a cell, module or array as a continuous function for a given set of operating conditions. The output current of the PV cell can be calculated using the equation;²⁻⁹

$I= I_{PV}- I_0\left[\exp \left(\frac{q\left(V+R_S*I\right)}{n*K*T}\right)-1\right]- \frac{\left(V+R_S*I\right)}{R_{SH}}$ (1)

The Double Diode Model (DDM) as shown in Figure 2 could give better I-V & P-V accuracy over SDM for low level irradiation.^3,5,7 The model is known as seven parameters model and the seven parameters are : I₀₁ represents the first diode reverse saturation currents, I₀₂ the second diode reverse saturation current, a₁ and a₂ the two diode ideality factors, I_PV, R_S, and R_SH.¹⁶ The output current of the DDM can be expressed as^3,4,14,15

$I= I_{PV}- I_{01}\left[\exp \left(\frac{q\left(V+R_S*I\right)}{a_1*K*T}\right)-1\right]- - I_{02}\left[\exp \left(\frac{q\left(V+R_S*I\right)}{a_2*K*T}\right)-1\right]- \frac{\left(V+R_S*I\right)}{R_{SH}}$ (2)

Figure 2 Double diode equivalent circuit model of the PV.

Three diode model

The Three Diode Model (TDM) was first proposed by Nishioka et al.,²⁶ to account for the current leakage through the peripheries of a small sized solar cell. The parameter of this circuit is increased to 8 variable parameters and one fixed parameter. The variable parameters are : r for recombination ratio, J_01, J₀₂, J_0P are the first diode, second diode and third diode recombination current parameters respectively, R_P represents series resistance connected to the third diode, R_S1, R_S2, R_SH. The parameter of R_sub is set as a fixed parameter.²⁶ The TDM is depicted in Figure 3 and the output current can be defined by²⁵

$I=I_{PV}- I_{01}\left[\exp \left(\frac{q\left(V+R_S*I\right)}{a_1*K*T}\right)-1\right]- I_{02}\left[\exp \left(\frac{q\left(V+R_S*I\right)}{a_2*K*T}\right)-1\right]-I_{03}\left[\exp \left(\frac{q\left(V+R_S*I\right)}{a_3*K*T}\right)-1\right]- \frac{\left(V+R_S*I\right)}{R_{SH}}$ (3)

Figure 3 Triple diode equivalent circuit model of the PV.

The process of estimating parameters of PV models from measured I-V data and manufacturer’s datasheet is defined as “Parameter estimation problems of PV models”.³ However, when implementing the optimization algorithms subclass of Evolutionary Algorithms (EAs) to estimate PV parameters, the formulated problem is known as “Parameter optimisation problems of PV models”.^2,3 The procedure of implementing various EAs to accurately solve the given optimisation problems of PV models is based on fulfilling the three criteria’s of defining the solution of the chosen model (i.e SDM, DDM, TDM expressed in section 3.1.), Specifying the search range due to the stochasticity nature of EAs (detailed in sections 3.2.) and Setting a predefined objective function as detailed in section 3.3.²⁸ The main reason of using EAs, is to estimate optimal parameters of PV models, whereby the estimated parameter values from EAs are simulated. The difference between the experimental data curve and the calculated data curve is minimized using the objective function.²⁹

Solution for PV parameters extraction

The SDM, DDM and TDM are all expressed in Eqs. (1)-(3) as non-transcendental implicit equations of which has no expressible analytical solution for the current and voltage variable. In order to simplify the computational complexity and develop an explicit solution for the electrical models, the method of exchanging the calculated current parameter from the right hand side of Eqs. (1)-(3) with the experimental current data is adopted.³⁰ The newly re-written Eqs. (4)-(6) are known as the error function of the SDM, DDM and TDM. The derived error functions are given as the difference between the extracted and the experimentally measured current value.²⁹

For SDM,

$f_{SDM}\left(V,I, x\right)= I-I_{PV}+I_0\left[\exp \left(\frac{q\left(V+R_S*I\right)}{a*K*T}\right)-1\right]+ \frac{\left(V+R_S*I\right)}{R_{SH}}$ (4)                                                                  

For DDM,

${\text{f}}_{\text{DDM}}\left(\text{V},\text{I},\text{ x}\right)=\text{ I}-{\text{I}}_{\text{PV}}+{\text{ I}}_{01}\left[\exp \left(\frac{\text{q}\left(\text{V}+{\text{R}}_{\text{S}}\text{*I}\right)}{{\text{a}}_1\text{*K*T}}\right)-1\right]+{\text{ I}}_{02}\left[\exp \left(\frac{\text{q}\left(\text{V}+{\text{R}}_{\text{S}}\text{*I}\right)}{{\text{a}}_2\text{*K*T}}\right)-1\right]+\frac{\left(\text{V}+{\text{R}}_{\text{S}}\text{*I}\right)}{{\text{R}}_{\text{SH}}}$ (5)

For TDM,

${\text{f}}_{\text{TDM}}\left(\text{V},\text{I},\text{ x}\right)=\text{ I}-{\text{I}}_{\text{PV}}+{\text{ I}}_{01}\left[\exp \left(\frac{\text{q}\left(\text{V}+{\text{R}}_{\text{S}}\text{*I}\right)}{{\text{a}}_1\text{*K*T}}\right)-1\right]+{\text{I}}_{02}\left[\exp \left(\frac{\text{q}\left(\text{V}+{\text{R}}_{\text{S}}\text{*I}\right)}{{\text{a}}_2\text{*K*T}}\right)-1\right]+{\text{ I}}_{03}\left[\exp \left(\frac{\text{q}\left(\text{V}+{\text{R}}_{\text{S}}\text{*I}\right)}{{\text{a}}_3\text{*K*T}}\right)-1\right]+\frac{\left(\text{V}+{\text{R}}_{\text{S}}\text{*I}\right)}{{\text{R}}_{\text{SH}}}$ (6)

From the Eqs. (4)-(6), x represents a vector solution for each parameter extraction problem, whereby for the $SDMx=\left[I_{PV}{R}_S{R}_{SH}{I}_{0}a\right]$ , for the $DDMx=\left[I_{PV}{R}_S{R}_{SH}{I}_{01}{a}_1{I}_{02}{a}_2\right]$  and for the $TDMx=\left[I_{PV}{R}_S{R}_{SH}{I}_{01}{a}_1{I}_{02}{a}_2{I}_{03}{a}_3\right].$  The given solutions of Eqs. (4)-(6) are used by many authors of EAs for PV parameter estimation of the SDM, DDM and TDM.2,11,13,15,16,29,30 However, the solution presented by Khanna et al.,⁸ for the TDM is different because it accounts for 10 parameters as discussed form section 2 previously. The error function for the proposed TDM by Khanna et al.,⁸ is given in Eq (7).

For TDM- Khanna et al.⁸

$\begin{array}{l}{f}_{TDM}\left(V,I, x\right)= I-I_{PV}+ I_{01}\left[\exp \left(\frac{q\left(V+R_{S0}*I\left(1+K*I\right)\right)}{a_1*K*T}\right)-1\right]+I_{02}\left[\exp \left(\frac{q\left(V+R_{S0}*I\left(1+K*I\right)\right)}{a_2*K*T}\right)-1\right]\\ + I_{03}\left[\exp \left(\frac{q\left(V+R_{S0}*I\left(1+K*I\right)\right)}{a_3*K*T}\right)-1\right]+ \frac{V+R_{S0}*I\left(1+K*I\right)}{R_{SH}}\end{array}$     (7)

The following section defines the search ranges for the five parameters of the SDM and in some literatures the search range for the DDM.

Search bound range for PV parameters

When implementing Evolutionary Algorithms (EAs) to Eqs (4)-(6), it is important to define the search range of each individual parameter of PV models. The ranges are defined for the upper and lower bound search space to estimate accurately the desired PV parameter.³¹ Based on the PV cell technology, authors of different technical literature have adopted various assumptions to set the upper and lower bound search range. The most commonly used I-V experimental data is obtained from the PV cell technology of a 57 mm diameter silicon solar cell (R.T.C France) implemented by Easwarakhanthan et al.³² When using the R.T.C France experimental data, the decision variables for the SDM and DDM are given in the ranges below.

$\begin{array}{ccc}{I}_{PV}\in \left[0,1\right]\left(A\right),& I_0\in \left[0,1\right]\left(\mu A\right), & I_{01}\in \left[0,1\right]\left(\mu A\right), \\ I_{02}\in \left[0,1\right]\left(\mu A\right), & R_S\in \left[0,0.5\right]\left(\Omega \right), & R_{SH}\in \left[0,100\right]\left(\Omega \right),\\ a\in \left[1,2\right], & a_1\in \left[1,2\right], & a_2\in \left[1,2\right].\end{array}$

Results using this search range were implemented.⁶,²⁸,³⁰,³³−37 However, Hachana et al.,³⁸ presented similar search range for IPV and RSH as the previous authors for the 57 mm diameter silicon solar cell (R.T.C France), but proposed a broader search range for the series resistance (RS), diode currents (I0, I01, I02) and diode ideality factors (a, a1, a2) as given below:

$\begin{array}{ccc}{I}_{PV}\in \left[0,1\right]\left(A\right),& I_0\in \left[1e-9,1e-5\right]\left(A\right),& \\ I_{01}\in \left[1e-9,1e-5\right]\left(A\right),& I_{02}\in \left[1e-9,1e-5\right]\left(A\right),& \\ \begin{array}{l}{R}_S\in \left[0,1\right]\left(\Omega \right),\\ a\in \left[0.5,2\right],\end{array}& \begin{array}{l}{R}_{SH}\in \left[0,100\right]\left(\Omega \right),\\ a_1\in \left[0.5,2\right]\end{array}& \begin{array}{l}\\ a_2\in \left[0.5,2\right]\end{array}\end{array}$

Unlike Hachana et al.,³⁸ Ma J.,¹¹ defined and presented a much narrower search range for the 57 mm diameter silicon solar cell (R.T.C France) for the SDM and DDM as follows:

$\begin{array}{ccc}{I}_{PV}\in \left[0.7,1\right]\left(A\right),& I_0\in \left[1e-10,1e-4\right]\left(A\right),& \\ I_{01}\in \left[1e-10,1e-4\right]\left(A\right),& I_{02}\in \left[1e-10,1e-4\right]\left(A\right),& R_S\in \left[0.001,1\right]\left(\Omega \right),\begin{array}{cc}& R_{SH}\in \left[20,200\right]\left(\Omega \right),\end{array}\\ a\in \left[0.8,2\right],& a_1\in \left[0.8,2\right],& a_2\in \left[0.8,2\right].\end{array}$

Gong et al.,³⁴ and Chen et al.,³⁰ defined the search range for a 57 mm diameter silicon solar module (R.T.C France) as follows:

$\begin{array}{ccc}{I}_{PV}\in \left[0,2\right]\left(A\right),& I_{PV}\in \left[0,2\right]\left(A\right),& R_S\in \left[0,2\right]\left(\Omega \right),\\ R_{SH}\in \left[0,2000\right]\left(\Omega \right),& a\in \left[1,50\right].& \end{array}$

Hachana et al.,³⁸ presented the variable search range for SDM and DDM Photowatt PWP 201 PV module as follows:

$\begin{array}{ccc}{I}_{PV}\in \left[0,3\right]\left(A\right),& I_0\in \left[1e-12,1e-5\right]\left(A\right),& \\ I_{01}\in \left[1e-12,1e-5\right]\left(A\right),& I_{02}\in \left[1e-12,1e-5\right]\left(A\right),& \\ R_S\in \left[0,2\right]\left(\Omega \right),& R_{SH}\in \left[0,5000\right]\left(\Omega \right),& \\ a\in \left[0.5,2\right],& a_1\in \left[0.5,2\right],& a_2\in \left[0.5,2\right].\end{array}$

Ma J¹¹ proposed the search ranges for extracting both the SDM and DDM parameters narrower for the Photowatt PWP 201PV module which is made up of 36 polycrystalline silicon cells as follows:

$\begin{array}{ccc}{I}_{PV}\in \left[0.9,1.2\right]\left(A\right),& I_0\in \left[1e-10,1e-4\right]\left(A\right),& \\ I_{01}\in \left[1e-10,1e-4\right]\left(A\right),& I_{02}\in \left[1e-10,1e-4\right]\left(A\right),& \\ \begin{array}{l}{R}_S\in \left[0.001,1\right]\left(\Omega \right),\\ a\in \left[0.8,2\right],\end{array}& \begin{array}{l}{R}_{SH}\in \left[20,3000\right]\left(\Omega \right),\\ a_1\in \left[0.8,2\right],\end{array}& \begin{array}{l}\\ a_2\in \left[0.8,2\right].\end{array}\end{array}$  

Muhsen et al.,² assumed the SDM parameters search area for the KC120-1 multicrystalline 120 (Wp) PV module to be within the ranges as follows:

$\begin{array}{cccc}{I}_{PV}\in \left[1,8\right]\left(A\right),& I_0\in \left[1e-12,1e-5\right]\left(A\right),& R_S\in \left[0.1,2\right]\left(\Omega \right),& R_{SH}\in \left[100,5000\right]\left(\Omega \right),\end{array}\begin{array}{cc}& a\in \left[1,2\right].\end{array}$

Kashif et al.,¹³ proposed the parameter search range for six different PV technologies of thin film (ST36 and ST40), monocrystalline (SQ150PC and SM55) and multi-crystalline (S115 and S75). However the data obtained for these PV technologies were both synthetic and experimental data. The parameter search range for the synthetic data was set at a broader range given as follows:

$\begin{array}{ccc}{I}_{PV}\in \left[0,7.6\right]\left(A\right), & I_0\in \left[1e-12,1e-5\right]\left(A\right),& \\ I_{01}\in \left[1e-12,1e-5\right]\left(A\right),& I_{02}\in \left[1e-12,1e-5\right]\left(A\right),& \\ \begin{array}{l}{R}_S\in \left[0,1\right]\left(\Omega \right),\\ a\in \left[0.5,4\right], \end{array}& \begin{array}{l}{R}_{SH}\in \left[50,1000\right]\left(\Omega \right),\\ a_1\in \left[0.5,4\right],\end{array}& \begin{array}{l}\\ a_2\in \left[0.5,4\right].\end{array}\end{array}$

In the case of considering the experimental data obtained from the six different technologies, the search range is set by using the datasheet information to calculate the lower bound values. The lower bound values are determined using the following expressions:

$I_{PV,STC}=\left(I_{SC}+\Delta T*K_i\right)*\frac{G}{G_{STC}}$ (8)

$I_{0,STC}= I_{01}= I_{02}=\frac{\left(I_{SC}+\Delta T*K_i\right)}{{}_e{[\raisebox{1ex}{$(V_{OC}+\Delta T*K_V)$}\!\left/ \!\raisebox{-1ex}{$V_{th}$}\right.]}^{-1}}$ (9)

$R_{SH,STC}= \frac{V_{MP}}{I_{SC}- I_{MP}}- \frac{V_{OC}- V_{MP}}{I_{MP}}$   (10)

Where at STC ISC is the short circuit current, VMP voltage value at maximum power, IMP current value at maximum power, KV and Ki are temperature coefficient of voltage and current respectively. Eqs (8)-(10) are expressed at STC and as such, the series resistance equals zero. These established relationships helps setting the parameters search range as follows:

$\begin{array}{ccc}{I}_{PV}\in \left[0,2*I_{SC}\right]\left(A\right), & I_0\in [0,I0,STC*{10}^{(5)}](A),& \\ I_{01}\in [0,I0,STC*{10}^{(5)}](A),& I_{02}\in [0,I0,STC*{10}^{(5)}](A),& \\ \begin{array}{l}{R}_S\in \left[R_{S,STC}{}_{,}2\right]\left(\Omega \right),\\ a\in \left[0.5,4\right], \end{array}& \begin{array}{l}{R}_{SH}\in \left[R_{SH,STC,}1000\right]\left(\Omega \right),\\ a_1\in \left[0.5,4\right],\end{array}& \begin{array}{l}\\ a_2\in \left[0.5,4\right].\end{array}\end{array}$

Alam et al.,²⁹ defined the parameters search range for thin film (ST40), monocrystalline (SM55), multi-crystalline (KC200GT) and SM40_14A2 PV technologies similarly to Muhsen et al.,² using the assumptions of Eqs (8)-(10) at STC. The decision variable range is expressed as follows:

$\begin{array}{l}{I}_{PV}\in \left[0,2*I_{SC}\right]\left(A\right), I_0\in \left[0,1\right]\left(\mu A\right), \hfill \\ I_{01}\in \left[0,1\right]\left(\mu A\right), I_{02}\in \left[0,1\right]\left(\mu A\right), \hfill \\ R_S\in \left[0_{,}2\right]\left(\Omega \right), R_{SH}\in \left[0,5000\right]\left(\Omega \right),\hfill \\ a\in \left[1,4\right], a_1\in \left[1,4\right], a_2\in \left[1,4\right].\hfill \end{array}$

Cong et al.,³⁹ and Wei⁴⁰ replaced the STC conditions for Eqs(8)-(10) for a commercial silicon solar cell at temperatures 24oC to summarize the estimated parameters for the SDM. These estimated parameters of SDM were used for setting the parameters search range as follows:

1. IPV search range is set from ±1% to ±5% of the ISC value.
2. I0, I01, I02 search range is set from 0 to ±10% the ISC value.
3. RS search range is set from ±1% to ±5% of the measured slope parameter when voltage tends to VOC.
4. RSH search range is set from ±1% to ±5% of the measured slope parameter when current tends to ISC.
5. a, a1, a2 search range is set from ±0.5 to ±2.0.

Ishaque et al.,³¹ defined the search range of RS, RSH and a for mono-crystalline (SM55), multi-crystalline (S75) and thin film (ST40) PV technologies. Parameters of IPV and I0 are calculated from the estimated parameters of RS, RSH and a. The search ranges is set as follows:

$R_S\in \left[{0.1}_{,}1\right]\left(\Omega \right),R_{SH}\in \left[100,3000\right]\left(\Omega \right),a\in \left[1,2\right].$

Qin et al.⁴² presented similarly the search range as in the workings of Ishaque et al.,³¹ for the SDM for the three parameters of RS, RSH and a for a solar array field testing data. The search range was set as follows:

$R_S\in \left[0_{,}20\right]\left(\Omega \right), R_{SH}\in \left[10,200\right]\left(\Omega \right),a\in \left[0,2\right].$

Ma et al.¹¹,⁴² defined the parameters search range based on assumptions made from different technical literature. The PV module technologies in consideration are 57 mm diameter silicon solar cell (R.T.C France), Photowatt PWP 201 and KC200GT PV module. For SDM and DDM parameters the I0, I01 and I02 are assumed to be less than $50\mu A$ . photocurrent is assumed slightly larger than the ISC at STC. Series resistance is set to be less than $0.5\Omega$ . The ranges of shunt resistance RSH­ and diode ideality factor a are given as $R_{SH}\in \left[5,170\right]\left(\Omega \right),$ $R_S\in \left[0,0.5\right]\left(\Omega \right),$ $a\in \left[1,2\right],$ $a_1\in \left[1,2\right],$ $a_2\in \left[1,2\right].$

Similarly to the workings of Ishaque et al.,³¹ Ismail et al.,⁴¹ defined the search range for estimating three parameters of RS, RSH and a. The PV module technologies implemented were thin film (ST 40), multi-crystalline (Kyocera KC200GT) and monocrystalline (HIT-215). Parameter ranges are defined as follows:

$R_S\in \left[{0.01}_{,}1.2\right]\left(\Omega \right),R_{SH}\in \left[50,1000\right]\left(\Omega \right),a\in \left[1,2\right].$

Ishaque et al.,⁴⁴ defined the search range for both the synthetic and experimental data for the multi-crystalline (KG200GT) PV technology. The decision search range variables for the SDM and DDM are set as follows:

$\begin{array}{l}{I}_{PV}\in \left[8.18,8.25\right]\left(A\right), I_0\in \left[4e-11,4e-6\right]\left(A\right),\hfill \\ I_{01}\in \left[4e-11,4e-6\right]\left(A\right), I_{02}\in \left[4e-11,4e-6\right]\left(A\right),\hfill \\ R_S\in \left[0.1,0.6\right]\left(\Omega \right), R_{SH}\in \left[100,200\right]\left(\Omega \right),\hfill \\ a\in \left[0.95,1.1\right], a_1\in \left[0.95,1.1\right], a_2\in \left[1.1,2\right].\hfill \end{array}$

Muhsen et al.,⁴⁵ proposed a broader search space similarly to the Muhsen et al.,² for the 120 Wp multicrystalline KC120-1 PV module. The parameter search space for the SDM and DDM are given as follows:

$\begin{array}{l}{I}_{PV}\in \left[0,8\right]\left(A\right), I_0\in \left[1e-12,1e-5\right]\left(A\right),\hfill \\ I_{01}\in \left[1e-12,1e-5\right]\left(A\right), I_{02}\in \left[1e-12,1e-5\right]\left(A\right),\hfill \\ R_S\in \left[0,2\right]\left(\Omega \right), R_{SH}\in \left[100,5000\right]\left(\Omega \right),\hfill \\ a\in \left[1,2\right], a_1\in \left[1,2\right], a_2\in \left[1,2\right].\hfill \end{array}$

Han et al.,⁴⁶ proposed for the polycrystalline TSM-250PC05A PV module the search range much narrower for the SDM and DDM. The defined ranges are bounded as follows:

$\begin{array}{l}{I}_{PV}\in \left[0,10\right]\left(A\right), I_0\in \left[0,1e-7\right]\left(A\right), \hfill \\ I_{01}\in \left[0,1e-7\right]\left(A\right),I_{02}\in \left[0,1e-7\right]\left(A\right),\hfill \\ R_S\in \left[0,0.01\right]\left(\Omega \right),R_{SH}\in \left[0,10\right]\left(\Omega \right), \hfill \\ a\in \left[1,2\right], a_1\in \left[1,2\right], a_2\in \left[1,2\right].\hfill \end{array}$

Hultmann et al.,⁴⁷ set the search range for a PV system having 160 PV cells connected in series. The SDM search range is set as follows:

$\begin{array}{l}{I}_{PV}\in \left[0,1.5\right]\left(A\right), I_0\in \left[0,1e-6\right]\left(A\right), \hfill \\ R_S\in \left[0,0.5\right]\left(\Omega \right), R_{SH}\in \left[0,100\right]\left(\Omega \right), \hfill \end{array}a\in \left[1,2\right].$

Dizqah et al.,⁴⁸ detailed the search range for the SDM similarly to Ishaque et al.,31 by setting the decision variable search range for RS, RSH and a. The three PV technologies used were polycrystalline KC200GT (Kyocera), thin film ST40 (SHELL) and monocrystalline E20/333 (Sunpower). Decision variable for KC200GT (Kyocera) is set as follows:

$\begin{array}{l}{R}_S\in \left[{0.001}_{,}1\right]\left(\Omega \right), R_{SH}\in \left[50,1100\right]\left(\Omega \right), \hfill \\ a\in \left[1,2\right].\hfill \end{array}$

Unlike Ismail et al.,⁴³ and Alam et al.,³⁰ as discussed previously, Dizqah et al.,⁴⁸ set the parameter range narrower. The setting of the thin film ST40 (SHELL) search range as compared to Ishaque et al.,³¹ and Kashif et al.,¹³ is considerable similar for the diode ideality factor and series resistance. However, the shunt resistance is noticeable set within a smaller range. The decision variables are given as follows:

$\begin{array}{l}{R}_S\in \left[{0.001}_{,}1\right]\left(\Omega \right), R_{SH}\in \left[50,550\right]\left(\Omega \right),\hfill \\ a\in \left[1,2\right].\hfill \end{array}$

The search range for the monocrystalline E20/333 (Sunpower) PV module is given as follows:

$\begin{array}{l}{R}_S\in \left[{0.001}_{,}2\right]\left(\Omega \right), R_{SH}\in \left[50,1500\right]\left(\Omega \right),\hfill \\ a\in \left[1,2\right].\hfill \end{array}$

Jiang et al.,⁴⁹ proposed the parameter search range for both the SDM PV solar cells and PV modules. A multicrystalline solar cell search range that is used for simulating experimental I-V data at different varied irradiance is defined as follows:

$\begin{array}{l}{I}_{PV}\in \left[0,5\right]\left(A\right), I_0\in \left[1e-12,1e-5\right]\left(A\right), \hfill \\ R_S\in \left[0,2\right]\left(\Omega \right), R_{SH}\in \left[50,5000\right]\left(\Omega \right), \hfill \\ a\in \left[0.5,10\right].\hfill \end{array}$

The search range for the 57 mm diameter silicon solar cell (R.T.C France)32 and a (78 x 24) mm multicrystalline solar cell is defined as follows:49

$\begin{array}{l}{I}_{PV}\in \left[0,2\right]\left(A\right), I_0\in \left[1e-12,1e-5\right]\left(A\right), \hfill \\ R_S\in \left[0,2\right]\left(\Omega \right), R_{SH}\in \left[10,500\right]\left(\Omega \right), \hfill \\ a\in \left[0.5,4\right].\hfill \end{array}$

A much wider search range is set especially for the shunt resistance RS and diode ideality factor a parameters is set for silicon solar module (R.T.C France)32 as follows:49

$\begin{array}{l}{I}_{PV}\in \left[0,2\right]\left(A\right), I_0\in \left[1e-12,1e-5\right]\left(A\right), \hfill \\ R_S\in \left[0,2\right]\left(\Omega \right), R_{SH}\in \left[50,5000\right]\left(\Omega \right), \hfill \\ a\in \left[0.5,100\right].\hfill \end{array}$

The search range proposed by Jiang et al.,⁴⁹ was given for a commercial silicon PV module (SL80CE36M) having 72 solar cells connected in series to implement for varied temperature and irradiance. The decision variable search range is set as follows:

$\begin{array}{l}{I}_{PV}\in \left[0,10\right]\left(A\right), I_0\in \left[1e-12,1e-5\right]\left(A\right), \hfill \\ R_S\in \left[0,5\right]\left(\Omega \right), R_{SH}\in \left[50,5000\right]\left(\Omega \right), \hfill \\ a\in \left[0.5,100\right].\hfill \end{array}$

Objective function
Objective function is usually introduced to effectively evaluate the performance of an implemented EA method.¹⁵ During the process of implementing EA, the defined objective function is minimized in respect to the given search range.²⁸ Among numerous published papers, the commonly used objective function is the Root Mean Square Error (RMSE)²,¹¹,¹³,¹⁵,²⁸−30,³²−38,⁴⁰,⁴⁴−47,⁴⁹−56. The RMSE is formulated to evaluate the deviation of the extracted parameter values from the experimental data.² The objective function defined as RMSE is represented by Eq. (11)

$RMSE= \sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^{N}J{\left(V, I, x\right)}^2}$  (11)

Where V and I are the voltage and current experimental values respectively; x is the vector that represents the PV model parameters that are optimized by the proposed EA.²,¹¹,¹³ Ideally the value of the RMSE is desired to be zero, because a smaller RMSE implies minimal deviation of the computed and experimental data.¹¹

The objective function sometimes referred to as the fitness function was proposed differently by Khanna et al.,⁸ as Mean Absolute Error (MAE). During the process of optimization, MAE is given as the measure of error and ideally desired to be zero value. MAE is defined by:

$MAE=\frac{{{\displaystyle \sum }}_{i=1}^N\left|I_{calculated- }{I}_{experimental}\right|}{N}$ (12)

Where, N represents the number of experimental points, Icalculated is the current calculated using the estimated parameters and Iexperimental represents the experimental current values.⁸ Awadallah et al.,¹² formulated the objective function as Relative Absolute Error (RAE). The RAE was chosen in by these authors because it requires no mathematical derivation, no testing and cover a wide range of operating conditions. RAE is represented as follows:

$RAE= {\displaystyle \sum }_{i=1}^4\frac{\left|X_{Ci}- X_{Ti}\right|}{X_{Ti}}$ (13)

Where the ith targeted and computed index is given as XTi and XCi respectively. Ishaque et al.,³¹ and Sudhakar et al.,⁵⁹ expressed the objective function (J) in terms of maximum power of PV module with respect to voltage in Eq(14).

$J=\left|\frac{dI}{dV}|{}_{(Vmp,\mathrm{Im}p)}+\frac{I_{mp}}{V_{mp}}\right|$ (14)

Where Vmp and Imp represents the voltage and current at MPP. Cong et al.,³⁹ Wei et al.,⁴⁰ and Ulaganathan et al.,⁶⁰ proposed the objective function for extracting the vector parameters x for the SDM as follows:

$H\left(x\right)= {\displaystyle \sum }_{i=1}^N{\left(I_c- I_m\right)}^2$  (15)

Where N is given as the data points, Ic and Im are the calculated and measured current respectively. Ismail et al.,⁴³ expressed the objective function for the experimental and calculated data as the average absolute error. The absolute error is calculated at different temperatures, irradiance and voltage. The average absolute error is given by:

$Erro{r}_{ave}= {\displaystyle \sum }_{j=1}^{p}abs\left(I_j\left(curve\right)-I_j\left(V_j,G_j, T_j,DV\right)\right)/p$ (16)

Where, p is given as the number of data points,
Ij is the experimental current or current obtained from manufacturer datasheet, Ij(Vj, Gj, Tj, DV) is the current at the specific irradiance Gj, voltage Vj, temperature Tj and at decision variable vector DV. Patel et al.,⁶¹ expressed the objective function similarly to Eq(16) at only the specified voltage Vk and vector variables. Eq(17) expresses the objective function at the total number of voltage points (p) as follows:

$F\left(X\right)=\frac{\left\{{{\displaystyle \sum }}_{k=1}^p{\left[I^{exp}\left(V_k\right)-I^{cal}\left(V_k,X\right)\right]}^2\right\}}{p}$ (17)

Patel et al.,⁶¹ proposed the objective function for the SDM similarly to the workings of Ismail et al.,⁴² for estimating three parameters of IPV, I0 and a at the specific voltage. The formulated objective function is given in Eq(18), taking into account the RS and RSH variables are fixed.

$F\left(X\right)= \raisebox{1ex}{$\left\{{{\displaystyle \sum }}_{i=1}^p{\left[I^{exp}\left(V_i\right)-I^{cal}\left(V_i\right)\right]}^2\right\}$}\!\left/ \!\raisebox{-1ex}{$p$}\right.$ (18)

Dizqah et al.,⁴⁸ introduces the phenomena of multi objective optimization problem (MOOP) by combining the conflicting objectives at STC and NOCT to formulate the objective function. The STC and NOCT objectives are given in Eq(19) and Eq(20) respectively:

$J_1\left(v_{pv}, i_{pv}\right)={\left[\frac{v_{pv}-V_{mpp,stc}}{V_{mpp,stc}},\frac{i_{pv}-I_{mpp,stc}}{I_{mpp,stc}},\frac{v_{pv}{i}_{pv}-P_{mpp,stc}}{P_{mpp,stc}}\right]}_2$ (19)

$J_2\left(v_{pv}, i_{pv}\right)={\left[\frac{v_{pv}-V_{mpp,noct}}{V_{mpp,noct}},\frac{i_{pv}-I_{mpp,noct}}{I_{mpp,noct}},\frac{v_{pv}{i}_{pv}-P_{mpp,noct}}{P_{mpp,noct}}\right]}_2$ (20)

The combined MOOP of both STC and NOCT objectives to formulate the objective function is given as follows:

$J\left(v_{pv}, i_{pv}\right)=\left\{w_1{\theta }_1{J}_1\left(v_{pv}, i_{pv}\right)+w_2{\theta }_2{J}_2\left(v_{pv}, i_{pv}\right)\right\}$ (21)

El-Naggar et al.,62 Al Rashidi et al.,⁶² Louzazni et al.,⁶⁴ and Al Rashidi et al.,⁶⁵formulated the objective unction by summing up the individual absolute errors (IAEs) of a set number of experimental measurements. The objective function is given as follows:

$f= {\displaystyle \sum }_{i=1}^N\left|f\left(V_{Li},I_{Li},R_S,R_{SH},\dots \right)\right|$   (22)

Where VLi, ILi, N represents the experimental voltage, current and the number of experimental points respectively. Dkhichi et al.,⁶⁶ expressed the objective function as Sum of Squared Error (SSE) and is expressed as follows:

$g\left(I_{PV},V_{PV},\theta \right)={\displaystyle \sum }_{i=1}^N{\left[I_{PV mes-i}-f{\left(I_{PV},V_{PV},\theta \right)}_i\right]}^2={\displaystyle \sum }_{i=1}^N{\left[\epsilon {\left(I_{PV},V_{PV},\theta \right)}_i\right]}^2$ (23)

Where <$\theta$ represents the vector variables of parameters,$\epsilon$  accounts for the error between the experimental current $I_{PVmes-i}$  and calculated current, N is the number of experimental measured points. Wang et al.,⁶⁷ expressed the objective function for the SDM and DDM as follows:

$\theta =\arg minJ\left(\theta \right)$ (24)

Where $J\left(\theta \right)$  is represented in Eq(25) for the SDM and Eq(26) for the DDM.

$J\left(\theta \right)=\sqrt{\frac{1}{N}{\displaystyle \sum }_t{\left(I_t-I_{ph}+I_L\left\{exp\left[\frac{q\left(V_t+R_s{I}_t\right)}{akt}\right]-1\right\}+\frac{V_t+R_s{I}_t}{R_{sh}}\right)}^2}$ (25)

$J\left(\theta \right)=\sqrt{\frac{1}{N}{\displaystyle \sum }_t{\begin{array}{c}(I_t-I_{ph}+I_{L1}\left\{exp\left[\frac{q\left(V_t+R_s{I}_t\right)}{a_{1}kt}\right]-1\right\}+\\ I_{L1}\left\{exp\left[\frac{q\left(V_t+R_s{I}_t\right)}{a_{1}kt}\right]-1\right\}+\frac{V_t+R_s{I}_t}{R_{sh}}) \end{array}}^2}$ (26)

Hasanien68 proposed the objective function as power error. The formulated objective function minimizes the error between the maximum experimental power (Pmax,e) to the MPP maximum power output for the PV module (Pmax,m). The given objective function is written as follows;

$P_{max,m}=V_{mp}\left\{I_{PV}-I_0\left[\exp \left(\frac{V_{mp}+R_S*I_{mp}}{a*V_t}\right)-1\right]-\frac{V_{mp}+R_S*I_{mp}}{R_p}\right\}$ (27)

Qin et al.,⁴¹ presented the objective function for a single sampled point as follows

$f_i=\left|I^{*}-I_d\right|$ (28)

Where I* is given as the estimated load current and Id as the measured load current. The objective function implemented for estimating the N number of sample data points for the SDM parameter vectors is given as follows

$f=\sqrt{{\displaystyle \sum }_{i=0}^N{f}_i^2}$ (29)

This section has detailed the formulated the solution for deriving parameters of the PV model for the SDM, DDM and TDM. The search ranges of PV parameters has also been reviewed and compared for the different PV cells and modules technologies. The defined objective functions has been detailed and expressed mathematically as reviewed form different technical literatures. In the next section, EAs are classified and reviewed based on different author’s achievements and contributions.

The use of optimization algorithm for parameter estimation for PV cells and modules are attracting more attention, as the process of optimizing PV parameter values is achieved by minimizing the error between points of the simulated I-V curves and experimental I-V data. Computational process of EAs are achieved iteratively and inspired by different global optimization techniques.¹⁵⁻¹⁶ As compared to analytical and numerical methods, EA has shown better estimated parameters of PV in terms of computational efficiency, precision and accurate extraction of parameters^8,17. The flow process of estimating PV parameters for EAs from the initialization to achieving the optimal parameters can be seen in Figure 4.¹²

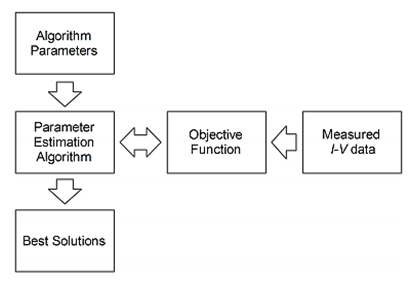
Figure 4 Flow diagram of PV parameter optimization.

The term Evolutionary Algorithms (EAs) have been used in several different terminologies.⁶⁹ EAs are known and sometimes classified to be bio-inspired based, swarm intelligence based, physics and chemistry based. Some authors have combined EAs with other EAs or numerical algorithms to form hybrid EAs.⁷⁰

This section reviews the different EAs implemented for the estimation of PV parameters in correspondence to their search range and objective function discussed in the previous sections 3.2 and 3.3.

Bio-inspired based EAs for PV parameter estimation

The most popularly used EAs for PV parameter estimations are bio-inspired based and have been adopted by several technical literatures as reviewed below. Zagrouba et al.,⁷¹ developed through the Matlab environment Genetic Algorithm (GA) to implement for the multi-crystalline silicon solar cell and the 50Wp PV module. The local minima solution for the estimation of the SDM cell parameters were reached after five generations and for the PV module, seven generations. Emphasis was laid on the mutation control parameter to be set between the ranges of 1% to 20% in order to avoid the local global convergence of PV parameters. Similarly to the workings of Zagrouba et al.,⁷¹ Ismail et al.,⁴³ programmed GA using the Matlab environment and also implemented GA for the SDM and DDM using the Matlab optimization toolbox. Parameter estimated were series resistance R_S, shunt resistance R_SH and diode ideality factor a. Results obtained showed an unbiased comparison between the two approaches, but rather gave a common argument on the SDM as having the most accurate results for both models. Jervase et al.,⁷³ also used the GA Matlab optimization toolbox by setting different control parameters as compared to the workings of Ismail et al.,⁴³ All seven parameters of the DDM I_PV, R_S, R_SH, I₀₁, a₁, I₀₂, and a₂ where extracted with minimal cost function. Patel et al.,⁶¹ implemented GA for extracting the SDM parameters of I₀, I_PV, and a. The GA control operators used was an elimination method for selection operator, random point crossover for crossover operator and single bit-flipping for mutation operator. PV technologies of silicon solar cell, plastic solar cell and polycrystalline solar cell were optimized using the objective function of Eq (17). Parameters of R_S and R_SH were obtained through the method of linear regression. Zhang et al.,⁷³ presented the conventional variant of GA that represents parameters as string of bits (0,1) for estimating the SDM parameters of series resistance R_S and diode ideality factor a. The proposed parameters to be estimated are encoded as 10 bits variable individually. GA algorithm optimized parameters for the Solarex MSX-60, BP380, BP3175 and Kyocera KC200GT PV modules. Ulaganathan et al.,⁵⁹ identified the limitation of using the conventional GA as having difficulties in representing the real value of variables because of the finite length of its bit string and proposed the GA algorithm that represents the decision variable parameters as having floating numbers. This GA is known as Real Coded Genetic Algorithm (RGA). The objective function is evaluated by using Eq (15) and the SDM parameters of I_PV, I₀, R_S, R_SH and a are represented as float point numbers. PV parameter results obtained showed better accuracy and faster computational when compared to results obtained from the conventional GA. Dizqah et al.,⁴⁸ proposed a non-conventional GA Matlab code for estimating the three parameters of R_S, R_SH and a for the SDM at both STC and NOCT. The variant of GA used disruptive selection to guarantee the reach of parameters to global optimum and also adds the advantage of parameter computational time not been dependent on parameter size. The need for improving GA has been proposed by different literatures by considering GA as a hybrid solution to numerical techniques to help improve its accuracy. Lingyun et al.,⁷⁴ modified GA into a new variant known as Adaptive Genetic Algorithm (AGA) whereby the crossover probability and mutation probability adjust adaptively. The numerical technique known as Nonlinear Least Square method (LS) is introduced as an LS operator that when applied to AGA, it operates as a GA mutation operator. Hybridization of AGA with the LS operator is known as GA-LS and was implemented with the objective function of Eq (11) to the 57mm diameter silicon solar cell (R.T.C France). Results obtained from GA-LS for the SDM when compared to the results of AGA gave minimal errors between the calculated and experimental I-V data. Maherchandani et al.,⁷⁵ proposed the hybridization solution by combining GA to Nelder-Mead algorithm known as GA-NM. For the SDM parameters GA was implemented to perform the search of global optimal parameters and NM to perform the local parameter search from the new parameter solution obtained from GA. furthermore, the need to improve upon the accuracy of parameters extracted by GA was proposed by Ishaque et al.⁴⁴ Differential Evolution (DE) was the bio-inspired EA implemented due to the similarity of its operators to GA. unlike GA that utilizes the crossover operator in the search space of parameters; the algorithm of DE relies and utilizes its mutation operator for both the selection and search mechanism. The comparison of results obtained when both the synthetic and experimental data of the commercial PV module (KC200GT) were evaluated by the objective function of Eq. (11), showed minimal errors for DE algorithm as compared to GA from the Matlab optimization toolbox. Tamrakar³⁴ also implemented DE similarly to the workings of Ishaque et al.,⁴⁴ but with different control parameters settings for the 57mm diameter silicon solar cell (R.T.C France). Results obtained were evaluated using the objective function of Eq. (13) for the SDM, DDM and when compared to GA and Particle Swarm Optimization (PSO) gave the most minimal errors. Ishaque et al.,³¹ highlighted the major problem of using conventional DE as convergence of parameters to local minimal prematurely and proposed the use a penalty function. The modified DE known as P-DE (penalty based differential evolution) was implemented to estimate the SDM three parameters of R_S, R_SH and a. the objective function of Eq(14) is used evaluate the experimental data obtained from the mono-crystalline (SM55), multi-crystalline (S75) and thin film (ST40) PV modules. Ishaque et al.,¹³ implemented the variant of P-DE because of its potential in evaluating parameters accurately at a given feasible region with constrained boundaries. The RMSE objective function was implemented to estimate all seven parameters of the DDM using the experimental data of six different PV technologies of; multi-crystalline (S75 and S115), mono-crystalline (SM55 and SQ150PC) and thin film (ST36 and ST40). Chellaswamy et al.,⁷⁶ identified the difficulties of setting the values of the control parameters of the conventional DE and proposed the variant of DE known as Adaptive Differential Evolution A-DE or Differential Evolution Technique (DET). The A-DE improves upon the conventional DE by changing the control parameters of crossover rates, mutation and population adaptively in accordance to the fitness values.

Jiang et al.,⁴⁹ modified the variant of DE known as Adaptive DEs (A-DE) that adjust the control parameters dynamically throughout the iteration process. The modification was to automatically and not adaptively adjust the settings of the control parameters of A-DE during the optimization process in accordance to the fitness values. This new variant of DE is known as Improved Adaptive Differential Evolution (IADE) with having dynamic control parameters that is selected through exponential functions and objective function expressed as RMSE. Gong et al.,³⁴ improved upon IADE by proposing the crossover rate repairing technique whereby the binomial crossover rate is repaired by using the average number of mutant components and the ranking based selection technique is adopted for the mutation operator, whereby the vector population is ranked in descending order form the best to the worst. This variant of DE is known as Improved Adaptive Differential Evolution with crossover rate repairing technique and ranking based mutation operator R_cr – IADE. The ranking based selection technique improves upon the computational complexity of extracting optimal parameters of the SDM and DDM for both the PV technologies of 57mm diameter silicon solar cell/module (R.T.C France) and Photowatt-PWP 201. Muhsen et al.,⁴⁵ proposed the hybridization of the conventional DE to with the electromagnetism-like (EM) algorithm that operates based on the concept of attraction and repulsion. This hybridized algorithm is known as Differential Algorithm with Integrated Mutation per iteration DEIM. The purpose of this combination is to improve upon the mutation process per iteration of algorithm by combining the mutation operator of the conventional DE with the mutation process of EM algorithm. Results obtained by simulating the synthetic data of the multi-crystalline 120Wp PV module with DEIM, showed faster convergence speed to extracting optimal PV parameters. Muhsen et al.,⁷⁷ hybridized EM with the conventional variant of DE known as DEAM. The computational process of DEAM is same for DEIM. Hultmann et al.,⁴⁷ proposed the hybridization of Free Search algorithm (FS) with the conventional DE and with Opposition Based Learning (OBL) known as FSDE. The value of the RMSE objective function obtained from FSDE showed minimal error when compared to other EAs algorithms. The FSDE pool of solutions is updated based on the updated Gaussian noise solution. Improvement made on the FSDE was for the pool of solutions to be updated by the best solution similarly as in DE. The improved FSDE is known as Improved Free Search Differential Evolution (IFSDE). Simulation of FSDE and IFSDE was implemented using the experimental data from the 160 Photovoltaic cells connected in series PV module. Hasanien⁶⁸ proposed the Shuffled Frog Leaping Algorithm (SFLA) that is developed based on the concept of observing and mimicking the behaviour of frogs when in search of local rich food source. The solution of SFLA can be affected by the number of frogs (P), iteration number before shuffling each memeplex (n), set value for the fitness tolerance and number of memeplexes (m). The optimal performance of SFLA for estimating optimal parameters of the SDM was obtained using the experimental data from the KC200GT and MSX-60 PV modules. Alam et al.,²⁹ proposed Flower Pollination Algorithm (FPA) for estimating optimal parameters for the SDM and DDM. The FPA operates based on four rules where rule 1 searches for the global pollination of flower, rule 2 searches for the local pollination, rule 3 represents the flower constancy and rule 4 switches the probability between the local and global searches. The optimal parameter values obtained from the SDM and DDM when compared to other EAs gave minimal RMSE values. Babu et al.,⁵⁸ further confirms the competence of FPA for estimating optimal parameters of PV technologies. The authors implemented FPA to the 57 mm diameter silicon solar cell/module (R.T.C France) similarly to the workings of Alam et al.,²⁹ for just the SDM. The algorithm of FPA ids faster convergences speed and higher accuracy for estimating PV models parameters. This section has reviewed bio-inspired EAs that have been implemented for estimating parameters of different PV technologies. Table 1 outlines and compares each bio-inspired EA.

The next section focuses more on swarming based EAs. In order to compare the accuracy of bio-inspired EAs, certain similarities such as the type of PV technology, the type of model at which the EA was implemented with, and the objective function used for algorithm evaluation are taken into consideration. The first comparison analysed is based on the algorithms which made use of the experimental data from the 57 mm diameter silicon solar cell and module (R.T.C France).

Swarm intelligence based EAs for PV parameter estimation

Similarly to bio-inspired EAs, swarming based EAs are modelled to mimic the swarming behaviour of birds, cats, bees and fish. Swarming based EAs have shown great potential in estimating PV parameters of the SDM, DDM and TDM. Qin et al.,⁴¹ presented the use of conventional Particle Swarm Optimization (PSO) due to the use of its social interaction among unsophisticated particles to find the global optimal parameters of the SDM. The PSO when evaluated with the objective function of Eq. (31) is used to estimate the parameters of R_S, R_SH and a. Wei et al.,⁴⁰ identified the limited potential of convention PSO proposed by Qin et al.⁴¹, as not having the proper mechanism of balancing exploration between the local and global search of particles. The solution proposed was to introduce the chaotic search strategy to the conventional PSO, whereby particles will be non-repeatable and the particle inertia is decreased linearly. The given algorithm of Chaotic Based PSO is known as CPSO and evaluated with the objective function of Eq. (17) is seen to have improved upon the convergence of global optimal parameters of PV and appropriate local convergence. The experimental data of the 57 mm diameter silicon solar cell (33ºC) and module (45ºC) (R.T.C France) is verified with the CPSO. Cong et al.,³⁹ confirms the accuracy and ability of CPSO as proposed by Wei et al.,⁴⁰ The CPSO control parameters, search range of parameters and objective function were set the same to estimate the SDM parameters of commercial silicon solar cell at 24°C. Ma et al.,⁵¹ proposed the variant of PSO that is combined with parallel global optimizer known as Parallel Particle Swarm Optimization (PPSO). During the implementation of the RMSE objective function, the particles of PSO are evaluated through parallel operations thereby utilizing more computation units and enabling PV parameters to converge to global optimal parameters. Results obtained for the SDM shows that, PV parameter estimation using the PPSO can significantly accelerate computational speed. Ma et al.¹¹ confirms the accelerated computational speed of PPSO as proposed by Ma et al.,⁵¹ for estimating the PV parameters for both the SDM and DDM. Hamid et al.,⁵² presented the varying of particle inertia weight and particle acceleration coefficient over the search ranges of particles. The given algorithm is known as PSO with varying inertia weight and acceleration coefficient (PSO-TVIWAC). Unlike CPSO proposed by Qin et al.,⁴¹ that decreases the particle inertia linearly, PSO-TVIWAC inertia weight is linearly varied to improve upon the global convergence of particles. The introduced accelerated coefficients help to control particles towards the global and local search space. Khanna et al.,⁹ presented PSO for the DDM and TDM. This variant of PSO concentrated more on the particle inertia weight to obtain a balance between the exploration and exploitation. It proposed the value of 1 to be assigned as the initial value of the particle inertia, and be decreased linearly to the value of 0. Results obtained after the implementation of the MAE objective function with the experimental I-V data obtained from a large area industrial silicon solar cell, showed the TDM outperformed the DDM in estimating PV parameters. Saravanan et al.,⁵³ proposed the hybridization of GA with PSO, thereby combining the strengths of both algorithms. The four combined operators of selection, crossover, mutation and enhancement are implemented for the KL070 PV module. Comparison of GA-PSO to GA shows minimal computational time and` better accuracy. Ma et al.,⁴² presented Cuckoo Search (CS) algorithm to outperform CPSO, GA and PSO. The CS is inspired by the breeding behaviour of certain species of cuckoos to detect the most successful pattern of parameters within the constrained defined search range. The lévy flight is initialized to aid global convergence of PV parameters. Results obtained for the SDM and ISDM, using the experimental data from the 57mm diameter silicon solar cell (R.T.C France) and the KC200GT module shows that CS outperformed CPSO. Jovanovic et al.,⁷⁸ identified the disadvantage of CS as not incorporating local search to improve and increase the speed of convergence when the constrained search is close to global or local minima but solely depend on lévy flight to generate new parameter solutions. The authors proposed the hybridization of

Nelder–Mead Simplex (NM) with CS known as CS-NM in other to improve upon the localized search of PV cells parameters. Han et al.,⁴⁶ presented the use of Artificial Fish Swarm Algorithm (AFSA) for the SDM. The AFSA is inspired by the search behaviour of fishes when they head towards food, the fish swarming behaviour to avoid overcrowding that enhances stability to convergence, and following behaviour among fishes that improves upon the speed to convergence. In as much as results obtained from AFSA shows high efficiency for PV parameter estimations, the authors observed the gathering of some fishes in local optima which in turn slows down the convergence speed and proposed the addition of mutation operator (MO) to AFSA (MAFSA). This MO alters the artificial fish positions which in turns adjust the swarms and increase the speed of convergence. Oliva et al.,⁷⁹ presented the Artificial Bee Colony (ABC) algorithm for the SDM and DDM. ABC is inspired by the seeking of quality food source of honey bees. The three types of bees used were the employed bees, onlooker bees and scout bees. The three operational criteria for ABC is sending the employed bees, selecting the food source by using the onlooker bees and determining the global solution by scout bees. RMSE evaluation of ABC algorithm demonstrated higher accuracy in estimating PV parameters using the experimental data of the 57 mm diameter silicon solar cell (R.T.C France) and when compared to other EAs. Wang et al.⁶⁷ confirmed the potential and competence of Artificial Bee Colony (ABC) for the estimation of PV parameters. The three bees of employed bees, onlooker bees and scout bees were implemented for the iterative process of ABC. These bees had the advantage of amending their search position using their different trajectories. The authors proposed ABC to improve upon the balance between exploitation and exploration similarly to Khanna et al.,⁹ by proposing the best-so-far method. The implementation of ABC using the experimental data from the 57 mm diameter silicon solar cell (R.T.C France) when evaluated with Eq. (24) outperformed DE and PSO. Askarzadeh et al.,⁵⁵ presented Artificial Bee Swarm Optimization Algorithm (ABSO) for extracting PV parameters for the SDM and DDM. ABSO employs only the onlookers and scout bees for local and global optima parameter search unlike in the case of Wang et al.,⁶⁷ that employ three types of bees. The trade-off between balancing exploration which is the generation of new candidate solutions, to exploitation which is the concentration of algorithm search on the current good candidate solution, are defined by decreasing the linear function of global and local search. Chen et al.,³¹ proposed a novel hybrid algorithm based on a new three stage eagle strategy known as EHA-NMS is based on the hybridization of NMS and ABC. The novel algorithm focuses more on balancing exploitation with exploration thereby cascading the algorithm into the three stages of coarse exploration, coarse exploitation and fine exploitation. The stage of coarse exploration is initialized by ABC algorithm that is capable of global optimization but slowly convergence due to large computation. Second stage of coarse exploitation adopts multiple NMS and stage three uses a single adaptive NMS. Results obtained using the RMSE objective function and the experimental data from the 57mm diameter silicon solar cell (R.T.C France) and the photowatt-PWP 201 PV modules shows better convergence, reliability and accuracy of estimating PV parameters. Louzazni et al.,⁶⁴ presented the use of Firefly Algorithm (FA) for estimating parameters of the SDM. The FA is bound by the three rules of attractiveness among fireflies used to generate random sets of parameter solutions, the degrees of attractiveness among fireflies which computes the random trajectory among fireflies and the brightest firefly that updates the optimal set of parameter solutions. FA is implemented using the experimental I-V data from the 57 mm diameter silicon solar cell (R.T.C France) with IAE objective function. Results simulated for the SDM showed greater accuracy and convergence speed. Guo et al.,⁵⁶ proposed the Cat Swarm Optimization (CSO) for estimating the SDM and DDM PV parameters. The CSO is inspired by the swarming behaviour of cats. The search strategies of CSO are based on seeking mode, which represents exploration search process and tracking mode, which represents exploitation search process. The applied CSO to estimating PV parameters for the 57 mm diameter silicon solar cell (R.T.C France) provided better performance for consistency and convergence to global optimal parameters. Rajasekar et al.,⁸¹ presented Bacterial Foraging Algorithm (BFA) for estimating the SDM parameters of R_S, R_SH and a. The operators of BFA for the optimization process are chemotaxis, reproduction, swarming, elimination and dispersion. Results obtained from the PV modules of SM55, Shell ST40 and Shell S36 shows higher accuracy, consistency in solution but convergence slowly. Awadallah et al.,⁸¹ proposed that having a guided run of parameter solutions gives more minimal error as compared to random run. The algorithm presented the hybridization of PSO with Bacterial Foraging (BF) algorithm (PSO-guided BF). The PSO guides the direction of bacterium run which eventually enhances the search characteristics of BF to obtain global best parameter solutions. PSO-guided BF was implemented using the I-V data from the crystalline silicon LDK C1D2-140P PV module and objective function of RAE. The simulated results when compared to the given measured I-V data shows the most minimal error when compared to PSO and conventional BF. The next section details EAs inspired by physical and chemical processes for estimating PV parameters.

Chemistry and physics based EAs for PV parameter estimation

All EAs algorithms are not bio-inspired and swarming based but mimics certain physical or chemical laws for estimating PV parameters. El Naggar et al.,⁶² and Al Rashidi et al.,⁶³ proposed Simulated Annealing (SA) that is developed to mimic the gradual physical cooling process of a high quality crystal for estimating the SDM PV parameters. The SA identifies solutions that converge to local minimal to correspond to defect crystals and global optima solutions as perfect crystals. Experimental data obtained from the 57 mm diameter silicon solar cell (33ºC) and module (45ºC) (R.T.C France) was evaluated using the IAE objective function at irradiance of 1000W/m². Accuracy analysis for SA showed the least RMSE and MAE value when compared to other algorithms. Dkhichi et al.,⁶⁶ enhanced upon SA for estimating PV parameters by combining it to Levenberg – Marquardt (LM) method. The LM method has the combined but complementary features of steepest descent which has low sensitivity to initial values and Gauss-Newton that aids faster convergence. The hybridized method known as LM-SA relies upon the continuous adjustment settings of LM damping factor per iteration of SA. This method presented good accuracy for the SDM when evaluated using experimental I-V data of the 57 mm diameter silicon solar cell (33ºC) (R.T.C France) and Sum of Squared Error (SSE) objective function. Further analysis of LM-SA shows large computational memory of 2050 iterations to converge to global optimal solution. Askarzadeh et al.,²⁸ presented the algorithm of Harmony Search (HS) that is developed based on how musicians continuously try to find the perfect state of harmony pitches. The HS performance to global optimal solution is affected by the parameters of Harmony Memory Considering Rate (HMCR), bandwidth of generation (bw) and Pitch Adjustment Rate (PAR). The authors improved upon HS by proposing Grouping-based Global Harmony Search (GGHS) and Innovative Global Harmony Search (IGHS). The GGHS considered using worst harmonies to attain global optimal parameter solutions and employed the probabilistic selection criterion of tournament selection and roulette wheel. However, the IGHS considered a predefined number of best harmonies and applied the probabilistic approach of roulette wheel. The next category of EAs cannot be categorised based of swarming behaviour, physics or chemical process and bio-based, but fulfils the characteristics of EAs.

Other EAs for PV parameter estimation

There are some EAs that are not based on the previously discussed sections of bio-inspired, swarming, physical and chemical based. These algorithms are in accordance to the EAs characteristics of selection, reproduction and recombination. Askarzadeh et al.,³⁷ proposed Bird Mating Optimizer (BMO) that is developed based on four distinct search pattern mating strategies of four types of bird species. The four types of birds have the breeding process of monogamy, polygamy, polyandry and promiscuity. The advantage of using BMO is based on the assumption that a search space with different pattern maintains diversity and avoids premature convergence of parameters to local minimal. Estimated parameters results achieved for the SDM and DDM while using the experimental data from the 57 mm diameter silicon solar cell and module (R.T.C France), showed minimal RMSE values as compared to SA, HS, GGHS, IGHS and ABSO. Askarzadeh et al.,⁵⁵ identified the drawbacks of BMO as proposed in the workings of Askarzadeh et al.,³⁶ The authors identified that BMO has numerous adjustable parameters and numerous types of birds. The simplified solution known as Simplified Bird Mating Optimizer (SBMO) is developed based on three bird species with the mating process of self breeding, one male and one female, one male and two females. The accuracy of SBMO is evaluated using the experimental data from the amorphous silicon PV module with 160 cells connected in series. Estimated PV parameters at different irradiance (1004.63 W/m², 1014.46 W/m², 1007.21 W/m², 204.53 W/m² and 203.22 W/m²) and temperature (25.01^oC, 40.01^oC, 55^oC, 25^oC and 35^oC) respectively showed minimal RMSE values. Yuan et al.,³⁵ proposed a novel biologically inspired algorithm known as Chaotic Asexual Reproduction Optimization (CARO). In the CARO, the asexual reproduction by which a parent produces offspring is the technique that balances exploration and exploitation. The chaotic sequence is introduced similarly to the workings of Wei et al.,⁴⁰ to limit parameters from converging to local optimal. The performance of CARO is evaluated using the RMSE objective function and the experimental data from the 57 mm diameter silicon solar cell (33ºC) and module (45^oC) (R.T.C France) at irradiance of 1000W/m². CARO is seen to outperform CPSO and SA by giving the most minimal RMSE value. Patel et al.,⁶⁰ presented the use of Teaching Learning Based Optimization (TLBO) for estimating PV parameters. The concept of TLBO is modelled based on the interaction and learning process between the teacher and learner in a classroom environment. TLBO has the advantage of having fewer control parameters that enables faster computational time process of the algorithm. The experimental data from four PV modules and cells, when evaluated with the objective function defined from Eq. (17) gave estimated PV parameters for the SDM. Chen et al.,⁵⁷ presented a novel algorithm known as Generalized Oppositional Teaching Learning Based Algorithm (GOTLBO). The new algorithm combines the Generalized Opposition Based Learning (GOBL) to the conventional TLBO. The GOTLBO employs the advantage of GOBL jumping parameter to enhance the convergence speed of TLBO. To verify the accuracy and competence of GOTLBO, the experimental data from the 57mm diameter silicon solar cell (33ºC) (R.T.C France) at irradiance of 1000W/m² is evaluated using the RMSE objective function. Results obtained for the SDM and DDM, shows that the GOTLBO is outperforms GA, CPSO, SA, IGHS, ABSO and R_cr-IJADE as having the least RMSE value.

The accurate estimation of PV parameters is an essential part to improve the efficiency of the PV system. In this paper, the different PV models have been described in details with the various assumptions. Furthermore, this study has reviewed the different EAs and discussed how to solve and optimise the PV parameters using EAs. The outline of different search ranges set for different PV technologies as well as their objective function are also presented. The influence of the control parameters setting and the effect of those for different algorithms have been analysed. Hybridized algorithm method have better accuracy in estimating PV parameters but are limited due to their slow computational speed. Algorithms with more search mechanisms such as in BMO are seen to converge more to global optimal solutions, and the opposite case applies to algorithms with insufficient search ranges operators. The fewer the control parameter of an algorithm has the less computational time.

None.

Author declares there is no conflict of interest in publishing the article.

1. Gorji TB, Ranjbar AA. A review on optical properties and application of nanofluids in direct absorption solar collectors (DASCs). Renewable and Sustainable Energy Reviews. 2017;72:10–32.
2. Muhsen DH, Ghazali AB, Khatib T, et al. A comparative study of evolutionary algorithms and adapting control parameters for estimating the parameters of a single-diode photovoltaic module’s model. Renewable Energy. 2016;96:377–389.
3. Jordehi AR. Parameter estimation of solar photovoltaic (PV) cells: A review. Renewable and Sustainable Energy Reviews. 2016;61:354–371.
4. Ishaque K, Salam Z, Taheri H. Accurate MATLAB Simulink PV system simulator based on a Two-Diode model. Journal of Power Electronics. 2011;11:179–187.
5. Salam Z, Ishaque K, Taheri H. An improved two-diode photovoltaic (PV) model for PV system, Joint International Conference on Power Electronics, Drives and Energy Systems (PEDES). 2010:1‒5.
6. Yoon Y, Geem ZW. Parameter optimization of Single-Diode model of Photovoltaic cell using Memetic algorithm. International Journal of Photoenergy. 2015:1–7.
7. Mahmoud SA, Alsari MM, Reda EI, et al. MATLAB modeling and simulation of photovoltaic modules. Proceedings of the 2012 IEEE 55th International Midwest Symposium on Circuits and Systems (MWSCAS). 2012:786-789.
8. Khanna V, Das BK, Bisht D, et al. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renewable Energy. 2015;78:105–113.
9. Soon JJ, Low K, Goh ST. Multi-dimension diode photovoltaic (PV) model for different PV cell technologies. IEEE 23rd International Symposium on Industrial Electronics (ISIE). 2014:2496‒2501.
10. Silva EA, Bradaschia F, Cavalcanti MC, et al. Parameter estimation method to improve the accuracy of Photovoltaic electrical model. IEEE Journal of Photovoltaics. 2015;6:278–85.
11.  Optimization approaches for parameter estimation and Maximum Power Point Tracking (MPPT) of photovoltaic systems. Ph.D thesis, University of Liverpool: UK. 2014.
12. Awadallah MA, Venkatesh B. Estimation of PV module parameters from datasheet information using optimization techniques. IEEE International Conference on Industrial Technology. 2015:2777‒2782.
13. Ishaque K, Salam Z, Mekhilef S, et al. Parameter extraction of solar photovoltaic modules using penalty-based differential evolution. Applied Energy. 2012;99:297–308.
14. Sandrolini L, Artioli M, Reggiani U. Numerical method for the extraction of photovoltaic module double-diode model parameters through cluster analysis. Applied Energy. 2010;87(2):442–51.
15. Ishaque K, Salam Z, Taheri H, et al. A critical evaluation of EA computational methods for Photovoltaic cell parameter extraction based on two diode model. Solar Energy. 2011;85(9):1768–1779.
16. Tamrakar R, Gupta A. A review extraction of solar cell modelling parameters. IJIREEICE. 2015;3(1);255–260.
17. Nassar-eddine I, Obbadi A, Errami Y, et al. Parameter estimation of photovoltaic modules using iterative method and the Lambert W function: A comparative study. Energy Conversion and Management. 2016;119:37–48.
18. Jolson Singh K, Kho KLR, Jitu Singh S, et al. Artificial neural network approach for more accurate solar cell electrical circuit model. International Journal on Computational Science & Applications. 2014;4(3):101–16.
19. Azzouzi M, Popescu D, Bouchahdane M. Modeling of electrical characteristics of Photovoltaic cell considering Single-Diode model. Journal of Clean Energy Technologies. 2016;4:414–420.
20. Adamo F, Attivissimo F, Di Nisio A, et al. Parameters estimation for a model of photovoltaic panels. Portugal: XIX IMEKO World Congress Fundamental and Applied Metrology; 2009. 6‒11.
21. Wang Y, Zhao J, Qu K, et al. A new approach for silicon solar cell model analysis and parameter correction. 2nd IET Renewable Power Generation Conference. 2013 Sept 9-11; china.1‒4.
22. Varshney SK, Khan ZA, Husain MA, et al. A comparative study and investigation of different diode models incorporating the partial shading effects. International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT). 2016 March 3-5; India. 3145-3150.
23. Ma J, Man KL, Ting TO, et al. Approximate Single-Diode Photovoltaic model for EfficientIy Characteristics estimation. The Scientific World Journal. 2013:1–7.
24. Cotfas DT, Cotfas PA, Kaplanis S. Methods and techniques to determine the dynamic parameters of solar cells: Review. Renewable and Sustainable Energy Reviews. 2016;61:213–221.
25. Sarkar MNI. Effect of various model parameters on solar photovoltaic cell simulation: A SPICE analysis. Renewables: Wind, Water, and Solar: 2016.
26. Nishioka K, Sakitani N, Uraoka Y, et al. Analysis of multicrystalline silicon solar cells by modified 3-diode equivalent circuit model taking leakage current through periphery into consideration. Solar Energy Materials and Solar Cells. 2007;91(13):1222‒1227.
27. Azab M. Improved circuit model of photovoltaic array. International journal of electrical power and energy systems engineering. 2009;2:185‒188.
28. Askarzadeh A, Rezazadeh A. Parameter identification for solar cell models using harmony search-based algorithms. Solar Energy. 2012;86(11):3241‒3249.
29. Alam DF, Yousri DA, Eteiba MB. Flower pollination algorithm based solar PV parameter estimation. Energy Conversion and Management. 2015;101:410–422.
30. Chen Z, Wu L, Lin P, et al. Parameters identification of photovoltaic models using hybrid adaptive Nelder-Mead simplex algorithm based on eagle strategy. Applied Energy. 2016;182:47–57.
31. Ishaque K, Salam Z. An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE). Solar Energy. 2011;85:2349–2359.
32. Easwarakhanthan T, Bottin J, Bouhouch I, et al. Nonlinear Minimization algorithm for determining the solar cell parameters with microcomputers. International Journal of Solar Energy. 1986;4:1–12.
33. Tamrakar R, Gupta A. Extraction of solar cell Modelling parameters using differential evolution algorithm. IJIREEICE. 2015;3:78–82.
34. Gong W, Cai Z. Parameter extraction of solar cell models using repaired adaptive differential evolution. Solar Energy. 2013;94:209–20.
35. Yuan X, He Y, Liu L. Parameter extraction of solar cell models using chaotic asexual reproduction optimization. Neural Computing and Applications. 2015;26:1227–39.
36. Askarzadeh A, Rezazadeh A. Extraction of maximum power point in solar cells using bird mating optimizer-based parameters identification approach. Solar Energy. 2013;90:123–33.
37. Zhang Y, Lin P, Chen Z, et al. A population classification evolution algorithm for the parameter extraction of solar cell models. International Journal of Photoenergy. 2016;1–16.
38. Hachana O, Hemsas KE, Tina GM, et al. Comparison of different metaheuristic algorithms for parameter identification of photovoltaic cell/module. Journal of Renewable and Sustainable Energy. 2013:5.
39. Cong J, Lingyun X, Deyun S, et al. Solar cells performance testing and modelling based on particle swarm algorithm. 2012:562‒566.
40. Wei H, Cong J, Lingyun X, et al. Extracting solar cell model parameters based on chaos particle swarm algorithm. 2011;27:398‒402.
41. Qin H, Kimball JW. Parameter determination of photovoltaic cells from field testing data using particle swarm optimization. IEEE Power and Energy Conference at Illinois. USA. 2011;1‒4.
42. Ma J, Ting TO, Man KL, et al. Parameter estimation of Photovoltaic models via cuckoo search. Journal of Applied Mathematics. 2013;362619.
43. Ismail MS, Moghavvemi M, Mahlia TMI. Characterization of PV panel and global optimization of its model parameters using genetic algorithm. Energy Conversion and Management. 2013;73:10–25.
44. Ishaque K, Salam Z, Taheri H, et al. Parameter extraction of photovoltaic cell using differential evolution method. IEEE Applied Power Electronics Colloquium (IAPEC). 2011 May 18-19; Malaysia. 10‒15.
45. Muhsen DH, Ghazali AB, Khatib T. Parameter extraction of photovoltaic module using hybrid evolutionary algorithm. IEEE Student Conference on Research and Development (SCOReD). 2015 Dec 13-14; Malaysia. 533‒538.
46. Han W, Wang HH, Chen L. Parameters identification for Photovoltaic module based on an improved artificial fish swarm algorithm. The Scientific World Journal. 2014;859239:1–12.
47. Hultmann Ayala HV, Coelho L dos S, Mariani VC, et al. An improved free search differential evolution algorithm: A case study on parameters identification of one diode equivalent circuit of a solar cell module. Energy. 2015;93(2):1515–1522.
48. Dizqah AM, Maheri A, Busawon K. An accurate method for the PV model identification based on a genetic algorithm and the interior-point method. Renewable Energy. 2014;72:212–222.
49. Jiang LL, Maskell DL, Patra JC. Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm. Applied Energy. 2013;112:185–193.
50. Ghani F, Duke M, Carson J. Numerical calculation of series and shunt resistances and diode quality factor of a photovoltaic cell using the Lambert w-function. Solar Energy. 2013;91:422–431.
51. Ma J, Man KL, Guan SU, et al. Parameter estimation of photovoltaic model via parallel particle swarm optimization algorithm. International Journal of Energy Research. 2015;40:343–352.
52. Hamid NFA, Rahim NA, Selvaraj J. Solar cell parameters extraction using particle swarm optimization algorithm. IEEE Conference on Clean Energy and Technology (CEAT). 2013; Malaysia. 461‒465.
53. Saravanan CA, Panneerselvam MA. comprehensive analysis for extracting single Diode PV model parameters by hybrid GA-PSO algorithm. International Journal of Computer Applications. 2013;78:16–19.
54. Askarzadeh A, Rezazadeh A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Applied Energy. 2013;102:943–949.
55. Askarzadeh A, dos Santos Coelho L. Determination of photovoltaic modules parameters at different operating conditions using a novel bird mating optimizer approach. Energy Conversion and Management. 2015;89:608–614.
56. Guo L, Meng Z, Sun Y, et al. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Conversion and Management. 2016;108:520–528.
57. Chen X, Yu K, Du W, et al. Parameters identification of solar cell models using generalized oppositional teaching learning based optimization. Energy. 2016;99:170–180.
58. Babu TS, Ram JP, Kumari N, et al. Solar PV parameter extraction using FPA. IEEE 6th International Conference on Power Systems (ICPS). 2016 March 4-6; India. 1‒6.
59. Ulaganathan M, Devaraj D. Real coded genetic algorithm for optimal parameter estimation of solar photovoltaic model. International Conference on Emerging Trends in Engineering, Technology and Science (ICETETS). 2016 Feb 24-26; India. 1‒6.
60. Patel SJ, Panchal AK, Kheraj V. Extraction of solar cell parameters from a single current–voltage characteristic using teaching learning based optimization algorithm. Applied Energy. 2014;119:384–393.
61. Patel SJ, Panchal AK, Kheraj V. Solar cell parameters extraction from a current-voltage characteristic using genetic algorithm. Journal of Nano-and Electronic Physics. 2013;5(2):2008‒2011.
62. El Naggar KM, Al Rashidi MR, Al Hajri MF, et al. Simulated Annealing algorithm for photovoltaic parameters identification. Solar Energy. 2012;86(1):266–274.
63. Al Rashidi M, El Naggar K, Al Hajri M. Extraction of Photovoltaic Characteristics using Simulated Annealing. 2nd Intl' Conference on Advances in Engineering Sciences and Applied Mathematics. 2014 May 4-5; Turkey. 1‒3.
64. Louzazni M, Craciunescu A, Aroudam EH, et al. Identification of Solar Cell Parameters with Firefly Algorithm. Second International Conference on Mathematics and Computers in Sciences and in Industry (MCSI). 2015 Aug 17; Malta. 7‒12.
65. Al Rashidi MR, Al Hajri MF, El Naggar KM, et al. A new estimation approach for determining the I–V characteristics of solar cells. Solar Energy. 85(7):1543–1550.
66. Dkhichi F, Oukarfi B, Fakkar A, et al. Parameter identification of solar cell model using Levenberg–Marquardt algorithm combined with simulated annealing. Solar Energy. 2014;110:781–788.
67. Wang R, Zhan Y, Zhou H. Application of artificial Bee Colony in model parameter identification of solar cells. Energies. 2015;8:7563–7581.
68. Hasanien HM. Shuffled frog leaping algorithm for photovoltaic model identification. IEEE Transactions on Sustainable Energy. 2015;6(2):509–515.
69. Simon D. Evolutionary Optimization Algorithms. USA: John Wiley & Sons; 2013. 772p.
70. Fister Jr I, Yang X, Fister I, et al. A brief review of nature-inspired algorithms for optimization. arXiv preprint arXiv:1307.4186.
71. Zagrouba M, Sellami A, Bouaicha M, et al. Identification of PV solar cells and modules parameters using the genetic algorithms: Application to maximum power extraction. Solar Energy. 84(5):860‒866.
72. Jervase JA, Bourdoucen H, Al Lawati A. Solar cell parameter extraction using genetic algorithms. Measurement Science and Technology. 2001;12(11):1922–1925.
73. Zhang Y, Lyden S, de la Barra, et al. A genetic algorithm approach to parameter estimation for PV modules. IEEE Power and Energy Society General Meeting (PESGM). 2016 July 17-21; USA. 1‒5.
74. Lingyun X, Lefei S, Wei H, et al. Solar cells parameter extraction using a hybrid genetic algorithm. Third International Conference on Measuring Technology and Mechatronics Automation genetic algorithm. 2011 Jan 6-7; China.
75. Maherchandani J, Agarwal C, Sahi M. Estimation of solar cell model parameter by hybrid genetic algorithm using matlab. International Journal of Advanced Research in Computer Engineering & Technology (IJARCET). 1:78‒81.
76. Chellaswamy C, Ramesh R. Parameter extraction of solar cell models based on adaptive differential evolution algorithm. Renewable Energy. 2016;97:823‒837.
77. Muhsen DH, Ghazali AB, Khatib T, et al. Parameters extraction of double diode photovoltaic module’s model based on hybrid evolutionary algorithm. Energy Conversion and Management. 2015;105:552–561.
78. Jovanovic R, Kais S, Alharbi FH. et al. Cuckoo Search Inspired Hybridization of the Nelder-Mead Simplex Algorithm Applied to Optimization of Photovoltaic Cells. arXiv preprint arXiv:1411.0217.
79. Oliva D, Cuevas E, Pajares G. Parameter identification of solar cells using artificial bee colony optimization. Energy. 2014;72:93‒102.
80. Rajasekar N, Kumar NK, Venugopalan R. Bacterial foraging algorithm based solar PV parameter estimation. Solar Energy. 2013;97:255‒265.
81. Awadallah MA, Venkatesh B. Bacterial foraging algorithm guided by particle swarm optimization for parameter identification of Photovoltaic modules. Canadian Journal of Electrical and Computer Engineering. 39(2):150–157.