The recent successes of British cyclists, in the Tour de France and Olympic Games, have resulted in an unprecedented increase in children taking up cycling in the UK. An increase in bicycle accident related head injury is inevitable and the focus will predictably turn to whether helmets optimally prevent injury. Many studies indicate that overall, head injury rates can be significantly reduced by their use. However, concerns remain that whilst preventing translational acceleration related head injury, bicycle helmets may actually increase the risk of angular acceleration related injury, due to their pronounced geometry. A 3D biofidelic-child-head form and two market-leading bicycle helmets were created in MSC ADAMS^TM, to investigate the potential effects of helmet geometry on head impact induced loading. Helmet safety standards for angular acceleration exposure do not currently exist, therefore, three oblique impact tests were established, representing the three anatomical-axes. Peak impact angular and linear accelerations were compared between un-helmeted and helmeted head forms. Bicycle helmets reduced linear and angular accelerations by an average 54 g and 3295 rad/s², respectively. The overall reduction in angular acceleration was, however, modest. Thus, it is recommended that International test standards be urgently revised to include measures to encourage a further reduction in exposure.

Keywords: Biomechanical; Bicycle helmet; Head injury; Children

The recent successes of British cycling, globally, have propelled cycling into the public consciousness, with an unprecedented increase in children taking up the sport.¹ An increase in bicycle accident related head injury is inevitable and the focus will inevitably turn to whether helmets optimally mitigate the seriousness of head injury in children. Whilst the popularity of bicycle helmets has risen steadily since their introduction in the 1970s, apparently correlating with a significantly reduced risk of head injury across all user groups,² questions remain as to whether, whilst reducing the incidence of direct focal impact injury, their pronounced geometry adequately mitigates or actually increases the risks associated with rotational head loading. The benefits related to mitigating focal impact may appear obvious, given a helmet effectively provides a ‘cushion’ between the head and an impact surface; however, debate as to their overall effectiveness remains within the scientific community.

During purely linear translational impacts, where the helmeted head strikes, or is struck by an object at an angle normal to the helmet surface and direction of travel, a bicycle helmet appears to be very effective at dissipating impact energy. Real-life accidents are rarely this simple, however, instead typically involving an oblique head impact ³ that produces a rotational torque on the helmet and thus, the head. Indeed, since angular brain acceleration can be more injurious than linear acceleration in impact scenarios,⁴ a helmet that can dissipate linear impact energy may either not sufficiently reduce, or may even increase, angular accelerations.

When wearing a bicycle helmet and being subjected to an oblique impact, it is hypothesized that the increase in ‘effective’ head diameter, that is, the head radius plus helmet thickness, may induce a greater head/brain rotational moment. This appears particularly pertinent when considering the relatively high increase in the effective head diameter created by children’s helmets. Epidemiology indicates that 10-year-old (males), are at greatest risk of sustaining a cycle related accident^5,6 hence, focus on suitable head protection for this age group of cyclists has the greatest potential to benefit society.^5-9

Whilst all bicycle helmets sold within the UK are subjected to two linear impact tests (BS: EN1078; British Standards 1997),¹⁰ there is no equivalent assessment of the helmet’s response to angular acceleration.

Whilst epidemiology identifies a need for helmet protection, it remains to be determined whether wearing a cycling helmet will sufficiently reduce the head/brain accelerations and minimize the injury risk. Indeed, Curnow,¹¹ has previously argued against helmet use, given the inability of previous epidemiological research to distinguish between head injury and brain injury and that previous research using meta-analysis does not provide the scientific evidence to support the current helmet designs.

Thus, while researchers broadly agree that bicycle helmets appear to reduce overall head injury, they have failed to agree that helmets do not pose an increased risk of angular acceleration induced brain injury. Hence, this study investigates whether a child’s helmet use is increasing the relative risks of brain injury through rotation, or whether this risk is outweighed by the benefits of reduced linear impact acceleration.

A three dimensional (3D) biofieldic head form, representing a 50th percentile male 10-year-old, was produced, conforming to the dimensions required for the Hybrid III (Mertz et al)¹² using Solidworks^TM, which was modified to conform to required dimensions:- overall curvature and shape of an established EN960 head form.¹³ A number of previous studies^14,15 were utilised to ensure the head form was suitably biofidelic, data to describe the head mass distribution was then derived from the most comparable head [12], that is, 3.66 kg compared with 3.67 kg.^14,15 Additional verification was sought by comparison to the head mass of the ‘Small Female’ (that is, 5th percentile) Hybrid III dummy,¹⁶ which is identical to that of the Hybrid III 10-year-old. For consistency, centre of mass values were utilized from the above Hybrid III head form. Inertial parameters were used from the heads between 3.6 and 3.7 kg.¹⁴

Whilst the skull stiffness varies across the head surface, with the temporal region recognised as being one of the weakest areas,¹⁷ a lack of literature meant it was impossible to quantify a child’s skull stiffness. Instead, an average value of 583.4 N/mm was calculated, based upon the minimum and maximum values reported from lateral, side and frontal loading of adult heads.^18,19 A 0.75 scaling factor was then applied to this data, to calculate the skull stiffness at 7 years of age.^20-22 In the knowledge that full skull stiffness is achieved at 20 years, interpolation was used to calculate a 10-year-old’s skull stiffness (471 N/mm). The model was then verified against EN960 stipulations, before being converted from a ‘shell’ to a ‘solid’ using the Solidworks^TM and then finally exported into the ADAMS^TM multi-body dynamics computer simulation software.

Two bicycle helmets were constructed by taking a series of accurate measurements. The two helmets were chosen from the five child size appropriate helmets investigated by St Clair & Chinn,²³ based on their perceived market exposure and highest and lowest monetary cost:

1. the Bell Faction^TM (most expensive) and
2. the ‘Bell Jumpstart^TM (least expensive), (an almost identical replacement of the Bell Bellino^TM, featured in St Clair & Chinn,²³ though no longer available at the time of testing) as shown in Figure 1.

Figure 1 Systematic representation of the Solidworks^TM helmet models.

It is also important to note that frictional coefficients were applied between each helmet and the ground (Bell Faction^TM = 0.58; Bell Bellino^TM = 0.66),²³ for consideration during the impact simulations. The helmet models were imported into the ADAMS^TM software and positioned with the centre of mass overlaying a ‘marker’ reference position. Validation was then performed by simulating an impact with a steel anvil, previously reported to produce AIS level 2 - injuries consistent with an impact of 100 - 150 g, at 2.2 m/s.²⁴ Impact velocities above 3.2 m/s correlated with AIS level 4, consistent with injuries from a 200 - 250 g impact.²⁴ Hence, the head form was dropped from heights of 0.247 m and 0.522 m to create impact velocities of 2.2 m/s and 3.2 m/s respectively. The contact parameters were iteratively revised to achieve successful validation. Defining the frictional coefficient between the human head and the impact surface required an appraisal of the literature; however, there is a wide range of skin friction values between μ = 0.5 and 1.1 ^25-27 although none describing interactions of the human scalp or hair, Hence simulations were performed with two different frictional coefficients:

1. μ = 0.7, higher than the helmet - anvil frictional coefficients,²³ hence representing a ‘worst case’ and
2. μ = 0.58, a value that broadly represents the mid-point between the ranges of head-anvil and helmet-anvil frictional coefficients.

The Bell Faction^TM model was positioned in a manner akin to the manufacturer’s fitting instructions. A void was present between the helmet and head form, which would normally be filled by comfort padding and hair. An iterative process was adopted to identify the helmet density, thereby enabling the ADAMS^TMsoftware to automatically calculate the inertial properties. The helmet was then rigidly constrained to the head form, to represent the ‘worst-case’ of zero slippage between the helmet and head during impact and thus, provide a comparison of the effects of geometric variation between helmets.

Validation of the head form-helmet construct was then performed against published experimental data.²³ The computational head form mass was increased to 4.2 kg and the inertial properties revised, using data acquired from,²⁸ to correlate to the head form properties, used during the experimental testing. Simulations were then conducted with an impact velocity of 5.42 m/s (that is, 1.5 m drop height) onto the side (temporal) region of the helmet and 4.57 m/s (that is, 1.0 m drop height) onto the front rim of the helmet (nose down), as shown in Figure 2. Acceleration values were compared to the published data and the helmet stiffness iteratively modified, until achieving successful validation. Once the appropriate contact properties for both the head and helmet had been determined, the head mass could be reduced back to that specified for a 10-year-old, allowing performance of oblique impact simulations for both the un-helmeted and helmeted head forms.

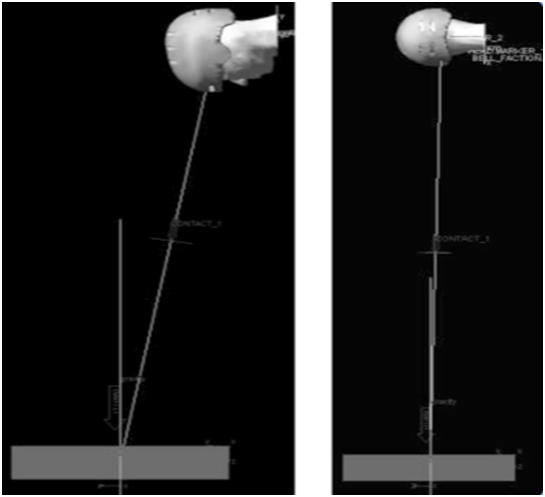
Figure 2 Helmet contact verification simulations, 4.57m/s frontal impact (left), 5.42 m/s side impact (right).

A motorcycle test (UN-ECE Regulation 22.05 - Method: A (United Nations, 1995)) was used to assess bicycle helmet performance, during oblique impacts, given that BS: EN1078 (British Standards, 1997)¹⁰ considers only linear scenarios. The test aims to re-create the impact sustained during a vertical fall of 0.25 m, while travelling at approximately 30 km/h (18.64 mph) (8.2 m/s), as shown in Figure 3. This protocol has also been used to consider the experimental performance of these same helmets.²³ In the Adams^TM simulation environment, this protocol translated to a drop height of 3.682 m, corresponding to 8.2 m/s, onto an impact surface inclined 15° from the vertical plane. The head form was first tested in isolation, prior to each helmet-head form construct tested against the oblique surface. Each test was repeated with the head form in three different orientations, to ensure that the impact generated head rotation in the three anatomical axes. The ‘nose-down’ impact, see Figure 4, was performed to induce sagittal plane head displacement, whilst the head form was rotated 90° for the ‘side’ impact test, to induce head rotation in the transverse plane, see Figure 5. The ‘vertex impact’ required the head form to be dropped vertically along an axis passing through both ears, causing an impact around the vertex of the head and thus, inducing head rotation about the frontal plane, see Figure 6.

Figure 3 Accident scenario, equivalent to Regulation 22.05 ‘Method A’ test.

Figure 4 Nose-down impact.

Figure 5 Side impact.

Figure 6 Vertex impact.

Each simulation reported the peak accelerations at the centre of mass of the head form, during each oblique impact scenario. Each simulation was run for 0.9 seconds with 1000 calculation steps. Further simulations were then performed to explore whether an increased effective head diameter would induce greater head angular acceleration. Using the ‘nose-down’ configuration, the properties of each helmet contact were changed to replicate the head contact. Although obvious that the helmet would not behave in the same way as the head in real life situations, the effect of a larger effective head diameter is of interest, with respect to the relative injury risk. Finally, simulations were performed to begin exploring the effect of design (geometry) on the induced angular acceleration, with the properties of the Jumpstart^TM helmet altered to represent those of the Faction^TM.

The un-helmeted and helmeted head form was impacted in 3 orientations with the oblique surface. The subsequent linear and angular accelerations are presented in Figures 7 & 8, respectively, with comparative Abbreviated Injury Scale (AIS) thresholds.²⁹ The results, describing simulations exploring the increased effective head diameter, are demonstrated in Figures 9 & 10. Figures 11 & 12 show the consequence of changing the properties of the Jumpstart^TM helmet, in turn, to equal those of the Faction^TM.

A series of simulations were conducted recreating three different types of un-helmeted head form and helmeted head form oblique impacts, with four different models. The resulting linear acceleration components for helmeted head forms, shown in Figure 7, are on average 25 g lower than a typical AIS = 1 injury, at 75 g, suggesting only a minor risk of injury. This is perhaps unsurprising, since the linear motion, normal to the anvil, equates to an impact velocity of only 2.2 m/s, also, the increased severity of linear acceleration demonstrated by the un-helmeted head forms, produced an average value of 129 g. This value correlates to AIS 2 injury risk, that is, moderate injury risk, associated with skull fracture.³⁰ The values for linear acceleration levels in oblique impacts support the evidence, that helmets are effective in reducing purely linear accelerations. This is unsurprising since bicycle helmets are generally optimized to dissipate energy in linear impacts.

Figure 7 Peak linear accelerations.

The results for angular acceleration at the head form centre of mass see Figure 8, show higher values for an un-helmeted head, than for a head form wearing a helmet in almost all cases. Interestingly, this result seems to challenge the initial hypothesis for which this study was based, that the effective increased diameter of the head would cause greater rotational torque on the brain during an impact. As shown by Figure 8, however, this is only true for a ‘side impact’, where the un-helmeted head had a co-efficient of friction equal to μ = 0.58 and the helmet (Bell Jumpstart^TM) produced an increased angular acceleration (1690 rad/s²). If, however, the helmet properties were modified, both in terms of stiffness and friction, to that of the μ = 0.7 head model, the initial hypothesis holds true.

Figure 8 Peak angular accelerations.

Figures 9 & 10 show the peak linear and angular accelerations observed when both helmets have modified ‘head’ properties. Angular accelerations vary more than their linear components, with the peak level at 19733 rad/s² for the Bell Jumpstart^TM, a level that is 3966 rad/s² higher than the μ = 0.7 head model, with identical contact and frictional properties. Accordingly, an increased effective head diameter does appear to increase angular acceleration levels measured at the head form centre of mass. However, this result also depends on a bicycle helmet having the same impact properties as the human head; a statement which is obviously untrue. The levels of angular acceleration observed for all impacts in Figure 8 are unsurprisingly large, since an applied Reg. 22.05 testing standard is designed for motorcycle helmets. All impacts register above the COST 327, AIS 1-2 level and most reach AIS 3-6.

Figure 9 Peak linear acceleration (nose-down) helmet with head properties

Figure 10 Peak angular acceleration (nose-down) helmet with head properties.

Interestingly, all impacts were predicted to be fatal, when compared with the angular acceleration/bridging vein rupture study of Löwenhielm³¹ and whilst the experimental shortcomings of this study are many, it does serve to illustrate that although the perpendicular impacts correlate with minor injury risk, angular accelerations produce a potentially greater injury risk. This is concerning, since during the majority of bicycle accidents the helmet will invariably impact another surface at an angle³ and current helmet designs are assessed against standards which measure their ability to reduce linear acceleration.

Since, the un-helmeted and helmeted models reacted so differently to each of the impact scenarios, it is important to identify which properties may have caused the difference in impact response. When comparing the un-helmeted head and Bell Faction^TM, with an identical frictional co-efficient (μ = 0.58), the un-helmeted head form still produced greater angular acceleration for all impacts. This suggests that although the coefficient of friction, between the surfaces, contributes to the production of angular acceleration, the difference in stiffness between each model also has a significant contributory effect. The stiffness of each helmet was almost one quarter that chosen for the head during the simulations. It was originally thought that the lower stiffness of the helmet model would encourage it to deform more easily, ‘gripping’ the abrasive anvil more effectively than the head model during an impact. As shown in Figure 8, however, the peak angular accelerations occurring in the helmeted head forms were generally lower. This may be explained by the peak head form deformation taking slightly longer to occur, due to increased helmet stiffness. Thus, the head form has an increased contact time with the anvil, before bouncing off. An increase in contact time is likely to result in greater transference of energy to the head, as shown by the greater induced linear accelerations in Figure 7 and in the case of an oblique impact; this would induce a greater angular acceleration at the centre of mass of the head form.

It is noteworthy, that the time of each acceleration peak did not match exactly between simulations. This is due to the difference in the geometry of each helmet and the way in which each head form was rotated and positioned (about the centre of mass for the head) between each impact scenario. Results show that the Jumpstart^TM helmet impacted onto the surface approximately 6 ms later than the Faction^TM. This difference equated to a 0.68% increase in impact velocity, since the drop height was effectively increased; however, this difference was so small the changes were considered negligible.

Only the ‘side impact’ scenario could be compared against experimental data.²³ The average experimental value, with a heavier 4.2 kg head form was 4859 rad/s², with the highest value being 6820 rad/s². The average between the two helmets in this study was 10769rads-2, with the highest equal to 12273 rad/s². This suggests that even though the head form, used for this study, was 0.54 kg lighter, higher angular accelerations were observed. To check that a heavier head form, similar to that used by St Clair & Chinn,²³ would increase angular acceleration, the head form model was altered to perform a side-impact scenario, with a head mass of 4.2 kg, corresponding inertial properties²⁸ and fitted with the Bell Faction^TM helmet. The resulting peak angular acceleration observed was 153 rad/s² higher for the 4.2 kg head form, thus indicating that the effect of head rotation, or slip, inside the helmet is an important factor to consider during oblique impacts. Subsequent modeling of an attachment system between the head and the helmet will be complex, as will defining the frictional properties between the scalp/hair and helmet. Even without modeling this interaction, however, it was still possible to demonstrate that angular acceleration is reduced, following helmet use, in all but one impact. As discussed above, the simulations demonstrated in this study were intended to investigate the geometric effects of helmet designs on translational and rotational head accelerations and represent a standard test ‘worst case scenario’, where the head is rigidly fixed to the helmet. Subsequently, whilst the angular accelerations observed may be slightly exaggerated, when compared to equivalent experimental data,²³ the findings of the study as a whole still indicate that helmet use reduces both linear and angular accelerations.

A series of further tests were performed to investigate the effect of specific helmet features. The Bell Jumpstart^TM performed poorly overall in both linear and angular acceleration categories, with an average linear response 5.6 g greater than the Bell Faction^TM and an average angular acceleration 2382 rad/s² greater. This result was considered a consequence of one or more of three possible variables:

1. The lower mass of the Jumpstart^TM in relation to the Faction^TM
2. The increased co-efficient of friction used for the Jumpstart^TM
3. The difference in external helmet geometry and thus, different impact site, in relation to the centre of mass of the head form.

To investigate the effects of these variables, the Jumpstart^TM side-impact scenario was modified to change individual variables and observe the result. The side-impact scenario was chosen, since this was the only scenario producing a greater angular acceleration, while wearing a helmet, compared to the same un-helmeted simulation. Figures 11 & 12 show a reduction in both linear and angular accelerations as various Jumpstart^TM helmet properties were altered, to match those of the Faction^TM. The most interesting result, shown in Figure 12, is the decrease in angular acceleration following an increase in helmet mass. This observation supports the claim by St Clair & Chinn²³ that increased helmet inertia would reduce the angular acceleration. The greatest reduction in angular acceleration to the Jumpstart^TM came from altering its coefficient of friction to equal that of the Faction^TM. This change lowered the linear and angular accelerations by 3 g and 1739 rad/s², respectively. This reflects the difference between each head model, with higher frictional co-efficient producing significantly higher angular and linear accelerations. Having now obtained acceleration values for an un-helmeted head, using biofidelic models, it is appropriate to comment on the differences between the values obtained here and those ‘predicted’ by the St Clair & Chinn,²³ who expected angular accelerations of 7500 rad/s² and 12000 rad/s² at linear accelerations of 100 g and 150 g during the Reg. 22.05 oblique impact scenario. To compare with the values found in this study, the linear and angular accelerations for each head form (Figures 7 & 8) were averaged between each impact situation. This produced linear accelerations of 124.6 g and 133.3 g for the μ = 0.58 and μ = 0.70 head forms, respectively. The associated average angular accelerations, for each of these head models were 12049 rad/s² and 15300 rad/s². If the St Clair & Chinn [23] angular acceleration predictions of between 100 g and 150 g are interpolated, it can be found that they²³ would predict angular accelerations of 9719.4 rad/s² and 10499.7 rad/s², at linear accelerations of 124.6 g and 133.3 g, found in this study, respectively. Therefore, the difference between the St Clair & Chinn²³ values and those found from this study for the μ = 0.58 and μ = 0.70 heads, are 2329.6 rad/s² and 4800.3 rad/s², respectively. Given that the St Clair & Chinn²³ effectively “estimated” the response of an un-helmeted head to oblique impact, their estimate appears to have been reasonable, according to the findings of this study. The closest matching angular acceleration value is that of the lower friction μ = 0.58 head but this is understandable, since the estimation was based on the response of helmets, which are likely to have a lower frictional co efficient than the un-helmeted head. It can be concluded, therefore, that the conclusions made by the St Clair & Chinn,²³ regarding the un-helmeted response of the human head to oblique impact are valid.

Given that the variation in results between the two un-helmeted head forms was significant, despite equal stiffness parameters, determination of more accurate frictional properties for the head form model would be beneficial to conduct further simulations and obtain more precise results.

Figure 11 Peak linear acceleration (side impact) altered Jumpstart properties.

Figure 12 Peak angular acceleration (side impact) altered Jumpstart properties.

Conducting multiple impact simulations of various scenarios, it was found that for oblique impacts, the use of a bicycle helmet generally lowers the magnitude of both linear and angular accelerations on the brain, agreeing with both Clair & Mills^23,22 and thus, disagreeing with the claims of Curnow.¹¹ This result occurred; even though the helmet-head form models were rigidly fixed, providing a “worst-case scenario” for rotation. During one simulation, the helmeted head form produced a greater angular acceleration; however, this increase was relatively small and would have not likely occurred had the model represented helmet slip over the head form. Since, in some cases, only a small difference occurred in angular acceleration, between helmeted and un-helmeted head forms, it is recommended that a specific oblique helmet impact test be incorporated into bicycle helmet test standards. Within our limited series of simulations, it was found that bicycle helmets with a low coefficient of friction, yet larger mass, offer a better form of protection against both rotational and translational brain injuries. The St Clair & Chinn²³ estimate of the response of the un-helmeted human head to oblique impact was sufficiently close to the findings from this study, providing the head has a low coefficient of friction (μ< 0.58) and a similar mass to that of a 10-year-old head (3.66 kg). Further research is now required to establish a more accurate approximation of chin-strap interaction and head friction, including hair and scalp movement.

None.

Author declares there is no conflict of interest in publishing the article.

1. Grous A. The Olympic Cycling Effect’ A report prepared for Sky and British Cycling. British cycling, USA; 2012. p. 1−15.
2. Dorsch M, Woodward A, Somers R. Do bicycle safety helmets reduce the severity of head injuries in real crashes? Accid Anal Prev. 1987;19(3):183−190.
3. Otte D. Injury mechanism and crash kinematics of cyclists in accidents. Proceedings of the 33rd Stapp car crash conference, SAE paper, USA; 1989. p. 20.
4. Chinn B, Canaple B, Derler S, et al. COST 327 - Motorcycle Safety Helmets. Luxembourg: European Commission. 2001.
5. Subhash P, Long J, Coffman S. Profile of pediatric bicycle injuries. South Medical J. 1998;91(11):1033−1037.
6. Klin B, Yehoshua RN, Kishk AI, et al. Bicycle-related injuries in children: Disturbing profile of a growing problem. Injury. 2009;40(9):1011−1113.
7. Williams M. The Protective Performance of Bicyclists’ Helmets in Accidents. Accid Anal Prev. 1991;23(2−3):119−131.
8. Ching R, Thompson D, Thompson R, et al. Damage To Bicycle Helmets Involved With Crashes. Accid Anal Prev. 1997;29(5):555−562.
9. Depreitere B, Lierde C, Maene S, et al. Bicycle-related head injury: a study of 86 cases. Accid Anal Prev. 2004;36(4):561−567.
10. British Standards Institution. Helmets for pedal cyclists and users of skateboards and roller skates. European committee for standardization. UK; 1997. p. 13.
11. Curnow WJ. The efficacy of bicycle helmets against brain injury. Accid Anal Prev. 2003;35(2):287−292.
12. Mertz H, Jarrett K, Moss S, et al. The Hybrid III 10 year-old Dummy. Stapp Car Crash J. 2001;45:319−328.
13. British Standards Institution BS EN 960. Headforms for use in the testing of protective helmets. BSI, UK; 2006.
14. Irwin A, Mertz H. Biomechanical Bases for the CRABI and Hybrid III Child Dummies. Proceedings of the 41st Stapp Car Crash Conference, Society of Automotive Engineers, USA; 1997. p. 12.
15. Yoganandan N, Pintar F, Zhang J, et al. Physical properties of the human head: Mass, center of mass and moment of inertia. J Biomech. 2009;42(9):1177−1192.
16. Mertz H, Irwin A, Melvin J, et al. Size, Weight and Biomechanical Impact Response Requirements for Adult Size Small Female and Large Male Dummies. Society of Automotive Engineers. USA; 1989. p. 16.
17. Yoganandan N, Pintar F. Biomechanics of temporo-parietal skull fracture. Clin Biomech. 2004;19(3):225−239.
18. Messerer O. Uber Elasticitat und Festigkeit der Menschlichen Knochen. Stuttgart Cotta, Germany; 1880. p. 140.
19. Elhaney J, Roberts V, Hilyard J. Handbook of Human Tolerance. Japan Automobile Research Institute, Japan; 1976. p. 631−641.
20. Kleinberger M, Yoganandan N, Kumaresan S. Biomechanical considerations for child occupant protection. Proceedings of the 42nd AAAM Conference, USA; 1998. p. 115−136.
21. Mohan O, Bowman B, Snyder R, et al. A biomechanical analysis of head impact injuries to children. Journal of Biomechanical Engineering. 1979;101(4):250−259.
22. Yoganandan N, Kumaresan S, Pintar F, et al. Pediatric biomechanics. In: Nahum A & Melvin J, editors. Accidental Injury. Springler Verlag, USA; 2000. p. 550−587.
23. Clair SV, Chinn B. Assessment of Current Bicycle Helmets for the Potential to Cause Rotational Injury. Project Report PPR 213, TRL Limited, UK; 2007.
24. Newman J. A Generalised Acceleration Model for Brain Injury Threshold (GAMBIT). Biokinetics and Associates Limited. Switzerland; 1986. p. 121−31.
25. Sivamani R, Goodman J, Gitis N, et al. Friction coefficient of skin in real-time. Skin Res Technol. 2003;9(3):235−239.
26. Zhang M, Mak A. In vivo friction properties of human skin. Prosthet Orthot Int. 1999;23(2):135−141.
27. Elert G. Coefficients of Friction for Human Skin, The Physics Factbook, An encyclopedia of scientific essays. 2005.  
28. Reynolds H, Clauser C, Conville J, et al. Mass distribution properties of the male cadaver. Highway Safety Research Institute, SAE Transactions 750424. USA; 1975. p. 1148−1150.
29. Association for the Advancement of Automotive Medicine. The Abbreviated Injury Scale 1990 Revision, Update 98, Des Plaines, IL: AAAM. 1998.
30. Hodgson V, Thomas L. Breaking strength of the human skull vs. impact surface curvature. National Academies of Sciences Engineering Medicine. USA; 1971. p. 189.
31. Löwenhielm P. Mathematical simulations of gliding contusions. J Biomech. 1975;8(6):351−356.
32. Mills N, Gilchrist A. Oblique impact testing of bicycle helmets. International Journal of Impact Engineering. 2008;35(9):1075−1086.