The prognosis of the results of treatment of the malignant new formations is a very important and vital problem of clinical oncology. The improvement of the existing methods of treatment and the development of new methods require the determination of the effective estimation of these methods. In this paper is presented the developed computer interpolation individualize precise prognosis. The use of a computer interpolation prognosis in the studies of the tumor new formations of lung, of the women and men breast cancer, ofcancer of egg, permitted to create the medico-mathematical model of tumor, which numerically reflects all laws of the course of tumor process after the conducted treatment. The course of tumor process after the carried out treatment is accompanied by the splash appearance of the first metastases and relapses in the group of the treated patients, and the time of the maximum number of patients of splash depends both from tumor itself and from the selection of the method of treatment. The computer interpolation prognosis proved the possibility of its use for determining the effectiveness of the used methods of treatment of the oncological patients. The conducted investigations using the computer interpolation prognosis showed the meaningful result of this prognosis wide practical realization. On the basis of obtained results the procedure, which permits to plan the optimum tactics of postoperative patient management, to select the periods of test survey and regimes of the preventive treatment of oncological patients, was developed. The results of scientific research permitted not only to reduce frequency, but also to considerably move aside the periods of the appearance of metastases. The obtained results became the basis for conducting the number of practical arrangements for periodic clinical observation and examination of oncological patients for the purpose of an improvement of the distant results of treatment.

Keywords: medico mathematical model of tumor, computer interpolation individualize precise prognosis, generalization, monitoring, postoperative treatment of patients, oncological patients

The prognosis of the results of treatment of the malignant new formations is a very important and vital problem of clinical oncology. The improvement of the existing methods of treatment and the development of new methods require the necessity for producing the effective estimation of these methods. Obtained in this case data permits not only to estimate the distant results of treatment by different methods, but also give the possibility to obtain similar results with the use of these methods of treatment subsequently. However, in the clinical practice the cases, when the method of treatment, which was proved as the effective among one patient, can be unsuccessful among another, frequently are encountered. This is connected with the fact that the conducted treatment influences not only on outcome of disease, but also on a significant quantity of other factors, which is determined in the final analysis of prognosis.

The conventional procedure of prognostication.^1–3 based on the estimation of the stage of process, cannot already satisfy clinicians due to its low accuracy. The latter fact causes that the domestic and international classifications of the stages of disease not only are based on the estimation of the extremely limited number of prognostic factors, but also allows the possibility of their arbitrary interpretation. By this the considerable disagreements of the results of evaluating one and the same methods of treatment on the material of the different authors are explained.

Furthermore, this method of prognostication (so-called general prognosis) has very essential deficiency: it does not permit to give the reliable evaluation of prognosis for each concrete patient. In connection with this the use in the clinic practice of the methods of the individual prognostication and of the results of treatment does not cause doubt. The importance of the individual determination of prognosis is explained by many circumstances.

First, the individual prognosis for each patient permits to select the group of patients, whose radical treatment would lead to the steadfast recovery, i.e. not less than 5years. These patients require neither the additional preventive treatment nor the too frequent test surveys, which, as it is known, are time-consuming and means.

In the second, for those patients, whose steadfast recovery by the existing methods of treatment cannot be attain, individual prognosis would give the establishment of the corresponding periods of examinations after treatment. A similar approach not only would help the development of the symptoms of the progression of tumor process in the earliest stages, but also would remove the necessity for carrying out frequent examinations during the first months after operation for those patient, for which is prognosticated the appearance of the distant metastases or relapse in the sufficiently distant periods.

Thirdly, the tactics of patient’s management in the postoperative period, based on the results of individual prognosis, would permit to avoid the unjustified or late use of preventive treatment, which with the specific circumstances can sharply decrease the immunobiologic resistibility of organism and lead to the progression of tumor process. The solution of the problem of individual prognosis was until recently hindered because of the necessity of conducting the complex (multifactor) analysis of the large number of prognostic symptoms.⁴ Widespread use in medical practice of the methods of computer mathematical modeling permits to develop the new methods of the individual prognosis of the treatment of a number of malignant new formations. The computer interpolation of appearance among oncological patient symptoms of progression of tumor process in different periods of time after operation is especially important prognosis. There is great interest in prognosis by the method of the computer interpolation of different factors among patients with the already evolved metastases

The studies of the influence of such factors as hormonal status, period of the appearance of metastases, presence of single or plural metastases on the prognosis of patients with the revealed metastases of lung cancer, of breast cancer of women and men, of malignant tumors of egg were conducted. The prognosis of the progression of tumor process among oncological patients in the clinical practice was accomplished on the base of All-Union Scientific Oncological Center of AMS of the USSR (Moscow, Russia) and Republic Clinical Oncological Dispensary (RCOD, Tajikistan).

Prognosis of the progression of tumor process among the patients of lung cancer after the surgical treatment

Depending on the selected control period of observation, the prognosis outcome of treatment was divided on the favorable and the unfavorable. The following periods were selected as the control terms: 5years, 18 and 36months based from the moment of operation. The selection of 5years period was established in clinical oncology as the criterion of steadfast recovery. The selection of 18 and 36monthly periods is connected with the carried out on the computer analysis of the progression of disease from different periods after operation.

Prognosis of the progression of the tumor process of breast cancer among women and men after the conducted treatment

The women, which belonged to the group of patients after conducted treatment, were investigated for the purpose of the prognostication of the appearance of the first metastases and relapse of breast cancer. For this, among the prognosticated symptoms, used in the clinical practice, were selected those, which proved or assumed influence on the course of disease after the conducted treatment. There were selected 614 symptoms from all. The estimation of the prognostic significance is conducted for each of them via the comparison of the frequency of appearance in the groups of patients with the progression of disease, which began during the periods up to 24months from the moment of operation, and among those, whom during this period metastases and relapse are not revealed. Information was taken from ambulant cards and histories of operated breast cancer patients (41 observations). The progression of disease began during the periods up to 24months based on the moment of operation among 18patients from them, and among 23patients the period of metastases and relapse was not revealed. Medico-mathematical analysis showed that 8symptoms more frequently lead to unfavorable outcome, basically the symptoms of the local spread of process, to the favorable outcome-12 symptoms, among which predominated the morphological characteristics of tumor and tissue of breast cancer

Prognosis of the progression of the tumor process of cancer of egg after the conducted treatment

The 231patients with the malignant of new formations of egg were located in RCOD. The patients had comprehensive clinical observations. All patients were divided on two groups: patients with the presence of primary tumor -154patients (66.7%), patients, who entered to the dispensary after the operation of orchiectomy or orchiecfnikulektomy from other therapeutic organizations-77patients (33.3%). In the conducted observations the malignant tumors of egg basically metastasized by lymphatic vessel, striking different groups of the lymph nodes: retroperitoneal -50.2%, mediastinum -4.3%, supraclavicular -10%, neck -0.3%, armpit -1%, inguinal -5.3%. The defeat of lungs and other organs frequently was met in the age from 20 to 45years. The teratomatous tumors more characteristically hit the internal organs -34.7%. The metastases defeat of internal organs by the seminoma tumors composed 23.5%. Frequently the teratoblastomas defeated the lungs -49%.

The interpolation method of the mathematical modeling was used for prognostication of the progression of the tumor process. The interpolation method of mathematical modeling is precise prognostication from the point of view of mathematics. The interpolation in the computational mathematics presents the method of finding the intermediate values ​​of the nodal points on the existing discrete collection of known values. Under conducting of scientific and engineering calculations, frequently necessary to operate with the collections of the values, obtained experimentally or by the method of random selection. As a rule, on the basis these collections necessary to construct the function, on which could with the high accuracy fall other obtained values. This task is called approximation.

The interpolation is called such variety of approximation, under which the curve of the experimentally constructed function runs accurately through the existing points of data (nodal points). Furthermore, the interpolation permits to predict (to extrapolate) the points of the experimentally constructed function out of the limits of the interval, under which the constructed function is assigned. The mathematical essence of interpolation consists of in the following.

Frequently is required to restore the function$f\left(x\right)$ for all values of хon the interval, $а\le х\le b$ , if its values are known in a certain finite number of points of this interval. These values can be found as result observations (measurements) in some full-scale experiment, or as result calculations.

Furthermore, the function$f\left(x\right)$ is calculated by formula and the calculations of its values in this formula are very labor-consuming; therefore it is desirable to have for the function the simpler (less labor-consuming for the calculations) formula, which would permit to find the approximate value of the considered function with the required accuracy at any point of interval.

As a result the following mathematical task is appeared. Assume that the interval is assigned by the grid $ώ=\{x_0=a<x<\mathrm{...}<{х}_{п}=b\}$ and in its nodal points are assigned by the values of function$y\left(x\right)$ , equal.

$y(x_0)=y_0,\dots ,y\left(x_i\right)=y_i,\dots ,y\left(x_n\right)=y_n$

Necessary to construct interpolant function$f\left(x\right)$ , which coincides with the function $y\left(x\right)$ in the grid points:

$f\left(x_i\right)=y_i,i=0,1,\mathrm{...},п$ (1)

The basic purpose of interpolation - to obtain the fast (economical) algorithm of the calculation of values for the values$f\left(x\right)$ , which are not contained in the table of data Basic question: how to select the interpolant $f\left(x\right)$  and how to estimate error $y\left(x\right)-f\left(x\right)$  The interpolating functions $f\left(x\right),$  as a rule, are built in the form of the linear combinations of some elementary functions

$f(x)={\sum }_{k=0}^n{c}_k{F}_k(x)$(2)

Where $F_k\left(x\right)-$  the fixed linearly independent functions, ${с}_0,{с}_1,\mathrm{...},{с}_n-$  not determined yet coefficients. Thus, we will obtain the system of $n+1$  of equations relative to coefficients $\left\{c_k\right\}:$

${\sum }_{k=0}^{n}ckFk(x(i))\infty$ (3)

Assume that system of functions ${\sum }_{k=0}^{n}ckFk(x(i))\infty$  is such, that with any selection of nodal points $а={х}_0<x_1<\mathrm{...}<{х}_n=b$

the determinant of the system is different from zero:

$F_0\left(x_0\right)F_1\left(x_0\right)F_2\left(x_0\right)\dots F_n(x_0)$

$\begin{array}{l}\Delta F=F_0\left(x_1\right)F_1\left(x_1\right)F_2\left(x_1\right)\dots F_n\left(x_1\right)\hfill \\ \hfill \end{array}$ (4)

$F_0\left(x_n\right)F_1\left(x_n\right)F_2\left(x_n\right)\dots F_n(x_n)$

Then on assigned$Y\left(i\right)$ are uniquely determined the coefficients${с}_{к}$ $(к=0,1,\mathrm{...},п)$ . The selection of the form of polynomial $F\left(x\right)$ defines the type of interpolation and on the obtained coefficients ck and its values at points it’s possible to determine $F\left(x\right)$ interpolation points.

The author5 developed the algorithm of the optimum interpolation of medical information. The modeling of the optimum calculation of the interpolation points of medical data was conducted via the comparison of all used by the algorithm interpolation methods on the error $y\left(x\right)-f\left(x\right)$  and the automatic selection of interpolation with the smallest value of error.

The following methods of interpolation were used: polynomial interpolation (polynomial of the type ${\sum }_{k=0}^n{c}_k{x}^{k}i$ of ), interpolation of Newton (Newton's polynomial), spline-interpolation, when between any adjacent grid points the function is interpolated by linear, cubic polynomial, by the polynomial of the first, third power (linear, cubic spline-interpolations), interpolation by the method of least squares (polynomial is calculated by this method) and interpolation by the method of the rational fractions (polynomial is calculated by this method).

Data input after statistical processing (after the program of the construction of histograms HIST).

The frequencies of oncological patients, i.e., a percent quantity of patients in the assigned interval of the predictable symptom on relation to all patients on all intervals of the predictable symptom are entered.
If the predictable symptom is the period of time of the appearance of metastases among oncological patients after the carried out treatment, then in percentage expression, the number of patients, distributed by the program of the construction of histograms, on the time intervals of the periods of the appearance of metastases after the carried out treatment, is entered (Figure 1).

Figure 1 Block-schema of the developed algorithm

Entered data become the nodal points for conducting the optimum interpolation.

The calculations consecutively produce the interpolation points and error $y\left(x\right)-f\left(x\right)$  by the methods of polynomial interpolation, by interpolation of Newton, by linear and cubic spline-interpolations, by the method of least squares interpolation and by the method of rational fractions interpolation until the optimum method with the minimum error will be determined.

The main and interpolation functions built the graphs according to obtained data of optimum interpolation and the numerical values of these functions are printed on the screen of the computer. The developed program of optimum interpolation was realized on the computer language C. The time of the calculations of program on the personal computer composes several seconds.

Up to present time in the literature⁶ the opinion of researchers, that the dependence of the periods of the appearance of metastases of tumors has an exponential form, i.e., the number of patients with the appeared metastases and a size of tumor exponentially fall in the course of time is encountered. However, still in 1991 the authors⁷ showed the first results of use the optimum interpolation for predicting the periods of the appearance of metastases among oncological patients after the carried out treatment and refuted this opinion. For the first time the specific period of the time, when is observed the splash (“hump”) of the number of patients with the appeared metastases after the carried out treatment, was shown. The use of the developed program of optimum interpolation for the prognosis of the progression of tumor process among oncological patients in the clinical practice was accomplished on the base of Republic Clinical Oncologic Dispensary (RCOD, Tajikistan). In this direction⁸ the studies of the influence of such factors as hormonal status, period of the appearance of metastases, presence of single or plural metastases on the prognosis of patients with the revealed metastases of lung cancer, of breast cancer of women and men and of the malignant tumors of egg were carried out.

Prognosis of the progression of tumor process among the patients of lung cancer after the surgical treatment

The solution of problem, which would determine the individual prognosis of the outcome of treatment among the patients of lung cancer, became possible due to realization on the personal computer of the developed program of optimum interpolation. Depending on the selected control period of observation, the prognosis outcome of treatment was divided on the favorable and the unfavorable. The following periods were selected as the control terms: 5years, 18 and 36months based from the moment of operation. The selection of 5years period was established in clinical oncology as the criterion of steadfast recovery. The selection of 18 and 36monthly periods is connected with the carried out on the computer analysis of the progression of disease from different periods after operation (Figure 2). It shows that the dependence of the periods of the appearance of metastases of tumors does not have exponential form, i.e., the number of patients with the appeared metastases of tumor exponentially does not fall during the time, but the “hump” of patients with the first metastases and the relapses of the group of the operated patients is determined. The peak of this “hump” was at the 21^stmonth in the range from 12 months to 30months after operation. Thus, the appearance of metastases and relapse among the oncological patients of lung cancer has to be most probably precisely during this period. Remaining splashes of (Figure 2) can be qualified as the small statistical fluctuations of the exponential decrease of the number of oncological patients with the metastases and the relapses. The conducted investigations permitted to develop new approaches to the postoperative of patient’s management after surgical operation and to the selection of the periods of test surveys after treatment. The patients with predicted favorable outcome don’t need frequent examinations during the initial 3 years after operation. During this period the examination is possible 1times/per half a year. The frequency of examinations should be increased in proportion to the approaching of 5years period. The frequency of examinations of patients with the predicted unfavorable outcome should be increased to the monthly control examinations with reaching of the periods of the prognostication of the appearance of metastases and relapse in the period from 12months to 30months and necessary to pay special attention to 21^st month. The use of the developed computer methods of the individual prognostication of the results of treatment is qualitatively new step in the solution of questions of patient’s management after the conducted radical treatment. This approach permits at the point of practicing doctor to develop the individual tactics of the patient’s management and to in proper time reveal the symptoms of the progression of tumor process.

Figure 2 Dynamics of the generalization of lung cancer in the group of patients after the conducted treatment (d - time of the splash of the maximum number of patients with the first metastases or relapse after the surgical operation).

Prognosis of the progression of the tumor process of breast cancer among women and men after the conducted treatment

The dynamics of the appearance of the first symptoms of the progression of disease in the group of the operated patients was investigated using the program of optimum interpolation. The results of studies are shown on Figure 3 shows that the splash “hump” of patients with the first metastases after operation is appeared in the period from 6.5months to 24months, and peak is fallen at the point of 18^thmonth. Remaining splashes of Figure 3 can be qualified as the small statistical fluctuations of the subsequent exponential decrease of the number of oncological patients with the metastases and the relapses. The dynamics of the generalization of breast cancer among men after the conducted treatment using the program of optimum interpolation was investigated on the base of data of Kiev Scientific Research Institute of Oncological and the Radiology (Figure 3). The results of studies showed that just as in the case with breast cancer among women the splash “hump” of patients with the first metastases after the conducted treatment is formed. The period of this splash is displaced to the right side in comparison with the case with breast cancer among women and composed period from 12months to 27months and peak of splash was fallen at the point of 22^ndmonth. The obtained results permitted to determine some approaches to their practical realization. The period of the appearance of “hump” of the generalization of breast cancer among women and men has to be used as the criterion for the selections of the regimes of the test surveys of patients and preventive treatment. The existing procedure of test surveys in the period after conducted treatment is into complete contradiction with obtained data. This procedure does not lead to the detection of the symptoms of the progression of disease before the period of the “hump” of metastases spreading and practically deprives of chances by patient, since during this period patients rarely are examined even with the annual intervals.

Figure 3 Dynamics of the generalization of breast cancer in the group of patients after conducted treatment (d - time of the splash of the maximum number of patients with the first metastases or relapse after conducted treatment)

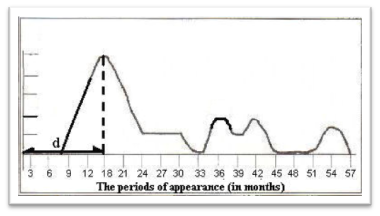
The developed approach is based on the principle of a maximum increase of the number of test surveys before the period “of the hump” of the generalization of tumor new formation. The obtained data about the period of the appearance of a “hump” of generalization can be criterion for the selection of the regimes of chemotherapy, conducted before the approaching of the “hump” of generalization. There are all reasons to expect that a similar approach will permit to considerably improve the results of treatment breast cancer among women and men.

Prognosis of the progression of the tumor process of cancer of egg after the Conducted treatment:

Computer interpolation prognostication was used for the development of the dynamics of the progression of the malignant tumors of egg and establishment of the real periods of conducting special antitumorigenic therapy after the operational removal of egg. The 104 patients with the reliably established periods of appearances metastases after the conducted treatment were processed. Not one of these patients for the moment of beginning treatment had the metastases. In this case the splash of patients “hump” with the appeared metastases in the group of the seminoma tumors of egg, that were subjected only of surgical treatment, was determined. The period of the splash of “hump” was 3-6months after operation on the primary tumor (orchiecfnikulektomy) and the peak of “hump” was reached at the point of 5^thmonth. For the teratomatous tumors of egg the dynamics of the development of primary metastases in the group only of operated patients took the following form: during the period from 3 to 5months was noted the splash the “hump” of patients from the moment of operation with the peak at the point of 4^thmonth. The splash “hump” of the patients, relative to patients, who received preventive medicinal treatment during the postoperative period, was noted and the period of the appearance of metastases was fallen at the point of the period from 8 to 10months with the peak at the point of 9^th month. This result testifies the effectiveness of use of the postoperative period of preventive chemotherapy and proves the ability of computer interpolation to evaluate the effectiveness of the conducted treatment.

In conclusion, it should be noted, that the use of a computer interpolation prognosis in the study of the tumor’s new formations of lung, breast cancer among women and men, malignant tumors of egg, permits to create the medico-mathematical model of tumor, which numerically reflects all laws of the course of tumor process after the conducted treatment. The course of tumor process after the conducted treatment is accompanied by the splash appearance of the first metastases and relapses in the group of the treated patients. The time of the maximum number of patients of splash depends both from tumor itself and from the selection of the method of treatment. Computer interpolation prognosis proved the possibility of its use for determining the effectiveness of the used methods of treatment of the oncological patients. The possibility of their wide practical realization is meaningful result of the conducted investigations. On the basis of obtained results was developed the procedure, which permits to plan the optimum tactics of patient postoperative management, to select the periods of test survey and regimes of the preventive treatment of oncological patients. The results of scientific research permitted to reduce frequency, but also to considerably move aside the periods of the appearance of metastases. The obtained results became the basis for conducting the number of practical measures for periodic observation and examination of oncological patients for the purpose of an improvement of the distant results of treatment.

None.

Author doesn’t have any relationships or interests that could have direct or potential influence or impart bias on the work. There is no conflict of interest.