The in situ study of chemical reactions kinetics has always been a great challenge. Here a modeling based on dynamic mechanical analysis (DMA) data of the natural rubber (NR) crosslinking reaction is presented and the order of reaction and reaction rate constant are determined.

Keywords: dynamic mechanical analysis, dicumyl peroxide, rheological, torque, correlation, viscosity, viscosimetric, polymerization, crosslinking

DMA, dynamic mechanical analysis; NR, natural rubber; EPR, ethylene propylene rubber; MFI, melt flow index; PE, polyethylene; EPDM, ethylene propylene diene monomer

The in situ determination of the chemical reaction kinetics in crosslinking or functionalization of polymer systems has been the subject of many recent studies. The decomposition of dicumyl peroxide during the crosslinking of NR was studied by Beyer.¹ The effect of temperature and processing on the chemical kinetics of the functionalization of EPR (Ethylene Propylene Rubber) was studied by Greco et al.²

The incorporation of rheological studies to follow the advancement of a chemical reaction was carried out by Ryan,³ who implemented a Viscosimetric technique that implied a correlation between chemical changes and rheological changes. Modeling of the PE (polyethylene) crosslinking reaction kinetics based on data obtained via torque and capillary rheometry was studied by Ortiz-Cisneros⁴ in order to obtain the order of reaction and the reaction rate constant.

Understanding of the interactions between the reaction kinetics⁵ and the rheological characteristics is very important, especially, for example, if it is a polymerization or a crosslinking reaction, in which case could result in great viscosity and/or temperature increases. Thus, the setup of the rheometric data and its correlation and presentation in the form of simple reaction kinetics is of the utmost importance for the purpose of mathematical modeling.

In any polymer system to undergo a crosslinking reaction, as the crosslinking density increases, the material moves from the rubbery to the glassy state. Therefore, the advancement of the chemical crosslinking reaction can be monitored through the continuous determination of the complex modulus $G^{*}$ or its components, the elastic $G^{\text{'}}$ and viscous $G^{"}$ moduli, in an oscillatory rotational rheometer.

$G^{*}=G^{\text{'}}+G^{"}$  (1)

From the rubber elasticity theory, the complex modulus, determined at very low deformations, can be related to the average number of crosslinks “$x$ ”, as observed in equation (4). Additionally, if the rate of crosslinks formation $\frac{dx}{dt}$ , is proportional to the number of crosslinks to be formed $x_{\infty }-x$ ; where$x_{\infty }$  represents the total number of crosslinks at the end of the reaction and$x$  represents the number of crosslinks at time t; and assuming that the kinetics of reaction follows the model of Kamal et al.⁵ it would result:

$\frac{dx}{dt}=\left(k_1+k_2{x}^m\right){\left(x_{\infty }-x\right)}^n$    (2)

m and n are material constants to be determined by experimental data, $k_1$  and $k_2$ should be directly related to the rate constant of the crosslinking reactions. It has been determined that there exists a relation between the exponents m and n such that m+n=3 C Scalan etal.⁶ and it has also been proposed Francois Chambon et al.⁷ that for some systems $k_1\cong 0$  After integration and solving for $x$ , it results:

$-\frac{x^{1-m}{\left(x_{\infty }-x\right)}^{-2+m}\left(x+\left(m-2\right)x_{\infty }\right)}{k_2\left(m-2\right)\left(m-1\right)x_{\infty }^2}=t+c$         (3)

If the reaction is treated as isothermic, then, the following equations apply:

$\left|G^{*}\right|=RTx$  (4)
$G_{\infty }^{*}=RT{x}_{\infty }$  (5)

Where $G^{*}$ and $G_{\infty }^{*}$ represent the complex modulus at a given reaction time and at the end of the crosslinking reaction. These two equations can be directly related to the crosslinking reaction kinetics.

The integration constant C can be evaluated by considering that at t=0,

$\left|G^{*}\right|=\left|G_{\infty }^{*}\right|$ .

This would give:

$-{\left(G_0^{*}\right)}^{1-m}{\left(G_{\infty }^{*}-G_0^{*}\right)}^{-2+m}\left(G_0^{*}+\left(m-2\right)G_{\infty }^{*}\right)=C$  (6)

In the case of the material used for this work, a gel point value of 1.60556 * 10³ Pa (150°C) was obtained, according to the technique mentioned by Tung and Dynes (Tung, C.-YM, Dynes, PJJ Appl Polym Sci 1982, 27, 569-574). When carrying out the experiment at 165°C, it is certain that it is above the gelation point of the material used. So that above the point of gelation

$G^{\text{'}}\gg G^{"}$ ,

thus, it can be considered that

$\left|G^{*}\right|\approx \left|G^{\text{'}}\right|$ ,

 therefore:

$$\begin{array}{l}-{\left(G^{*}\left(t\right)\right)}^{1-m}{\left(G_{\infty }^{*}-G^{*}\left(t\right)\right)}^{-2+m}\left(G^{*}\left(t\right)+\left(m-2\right)G_{\infty }^{*}\right)=\\ k_2\left(m-2\right)\left(m-1\right){\left(\frac{G_{\infty }^{*}}{RT}\right)}^{2}t-{\left(G_0^{*}\right)}^{1-m}{\left(G_{\infty }^{*}-G_0^{*}\right)}^{-2+m}\left(G_0^{*}+\left(m-2\right)G_{\infty }^{*}\right)\end{array}$$ (7)

It is important to mention that given the complexity of the equation, the nonlinear regression is performed as

$t=f{\left(G\right)}^{\text{'}}$

The polymers used were: a metallocene isotactic polypropylene, MR 2001, (mPP) from Atofina, USA, with a molecular weight Mw of 185,000 and a MFI (Melt Flow Index) of 25 g/10min (230°C and 2.16 kg); and a IP-4640 EPDM (Ethylene Propylene Diene Monomer) (EPDM-55), with ca. 5 wt% of ethylidene norbornene as the diene monomer, with an ethylene content of 55 wt% and a Mooney Viscosity ML(1+4) at 125°C of 40, from DuPont-Dow Elastomers, USA.

* P stands for being in pellets forms

We validated this model by monitoring the dynamic mechanical properties of the EPDM-55 formulation. We used an Anton Paar Physica rheometer with a cone and plate configuration at 165°C, within the linear viscoelastic region (Figure 1).

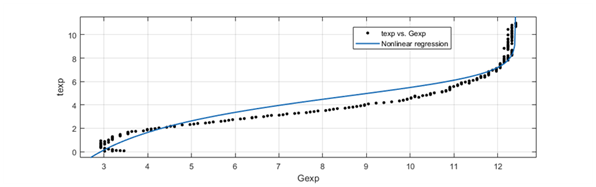
Figure 1 Shows the variation of G’ as the vulcanization (crosslinking reaction) of the sample proceeds, plus a nonlinear regression curve for the sample.

Data obtained from the nonlinear regression:
Coefficients (with 95% confidence bounds):
k=8.899e+04 (8.686e+04, 9.113e+04)
m=2.084 (2.066, 2.102)

The results of the linear regression can be corroborated by performing a dimensional analysis of equation (7), where the units of the kinetic constant are L² mol^-2 s^-1, which corresponds to a third-order reaction, according to the proposal that m+n=3. The reaction is of third order since more than one reagent is involved in which the initial reactants maintain different concentrations. The model proposed here conforms to the experimental data with a high level of precision. This is in agreement with the experimental data of vulcanization.

The kinetic data of a crosslinking reaction can be obtained by dynamic mechanical analysis. This can be extrapolated to monitor many other polymeric reactions in which there is a change in the complex modulus coupled with the progress of the chemical reaction.

None.

The author declares no conflict of interest.

1. Beyer G. Simulation of chemical kinetics of elastomer crosslinking by organic peroxides. Gummi Fasern Kunstst.1985;38:368–372.
2. Greco R, Maglio G, Musto PV. Bulk functionalization of ethylene-propylene copolymers I. Influence of temperature and processing on the reaction kinetics. J Appl Polym Sci. 1987;33(7):2513–2527.
3. Ryan ME. Rheological and heat transfer considerations for the processing of reactive systems. Polym Eng Sci. 1984;24(9):698–706.
4. Ortiz Cisneros JC. Simulación en extrusión reactiva de polietileno con peróxido de dicumilo, PhD thesis, Facultad de Ciencias Qu´ımicas, In Spanish: Universidad Aut´onoma de Coahuila; 1998.
5. Kamal MR, Seuror S. Kinetics and thermal characterization of thermoset cure. Polymer Eng Sci. 1973;13(1):59–64.
6. James C Scalan, H Henning Winter. Composition dependence of the viscoleasticity of end-linked poly(dimethylsiloxane) at the gel point. Macromolecules. 1991;24(1):47–54.
7. Francois Chambon, H Henning Winter. Linear Viscoleasticity at the Gel Point of a Crosslinking PDMS with Imbalanced Stoichiomestry. J Rheology. 1987;31(8):683–697S.